下颌平面角影响种植体应力分布的有限元分析

邢维斌郑淑贤杨适宜

1.天津市公安医院口腔科；2.天津大学机械工程学院，天津 300042

·口腔种植学专栏·

下颌平面角影响种植体应力分布的有限元分析

邢维斌1郑淑贤2杨适宜1

1.天津市公安医院口腔科；2.天津大学机械工程学院，天津 300042

目的 通过在不同下颌平面角角度下对下颌第一磨牙种植体的力学特性进行有限元分析，得出下颌平面角角度对种植体受力的影响规律，为临床种植提供理论参考。方法 采集3种不同下颌平面角（低角、均角、高角）CT数据，建立种植复合体有限元模型，设计正交实验方案，记录数据，分析处理，得出有限元分析结果。结果 最优参数组合为：低角，4.8 mm，Ⅱ型骨。各个因素的主次关系依次为种植体直径、下颌平面角角度、骨密度。结论 下颌平面角角度对种植体的稳固有一定的影响，在同样咬合力的情况下，高角种植体所受应力最大，其次是均角，低角最小。

下颌平面角； 种植体； 应力分布； 有限元分析

在临床实践中发现，根据患者的下颌平面角选择不同规格的种植体，种植体的长期成功率有所不同。因此有理由设想下颌平面角角度会影响下颌种植体的应力分布，进而影响种植成功率。本研究采用正交实验方法进行设计，利用有限元分析法对不同下颌平面角、不同密度下颌骨及不同规格种植体的力学特性进行研究，重点考察下颌平面角角度对种植体的应力影响规律，为临床种植选择提供参考。

1 材料和方法

1.1 实验材料

实验对象为不同下颌平面角角度、下颌骨密度以及种植体规格的9个种植复合体计算机模型。软件为Pro/E Wildfire5.0中的Mechanica分析处理器。

1.2 方法

1.2.1 确定实验因素值在临床上采集3种不同下颌平面角CT数据，测量下颌平面角角度分别为14°、22°、34°，以此作为实验角度（图1）；种植体选用的是ITI®公司生产的直径为3.3、4.1、4.8 mm的常规种植体；颌骨骨密度分为4种类型，因为临床上Ⅰ类骨所占比例极少，所以选取Ⅱ、Ⅲ、Ⅳ类骨作为实验对象[1]。

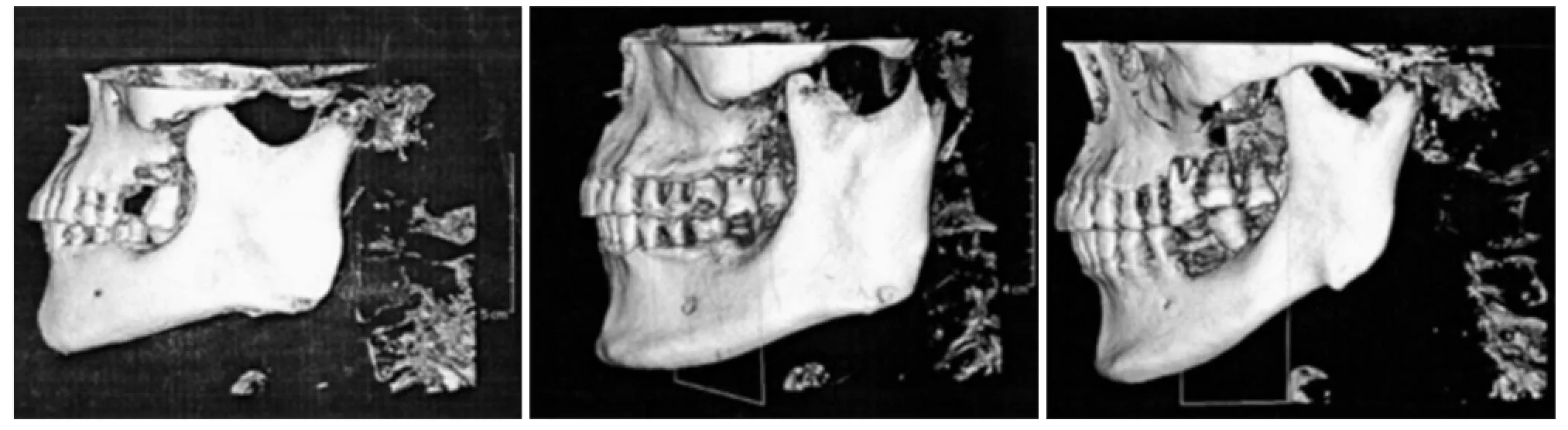
图 1 3种下颌平面角CT图像Fig 1 CT images of three different mandibular plane angles

1.2.2 设计正交实验 本次有限元分析正交实验涉及3个因素，每个因素分别对应3个水平（表1），根据正交表L9（33）[2]安排有限元分析实验计划（表2）。

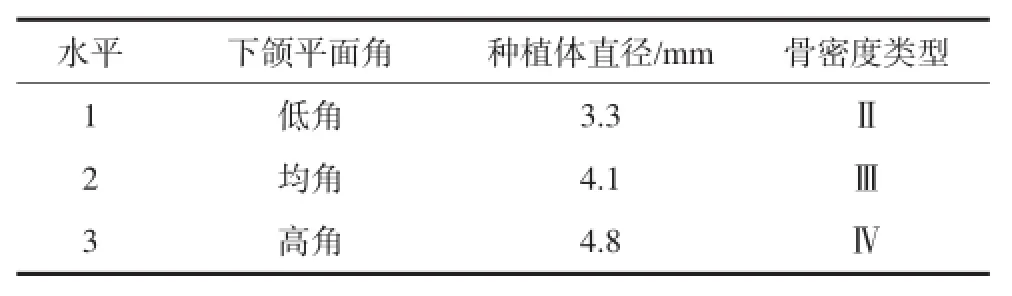
表 1 正交实验因素水平表Tab 1 Factors of orthogonal experimental research

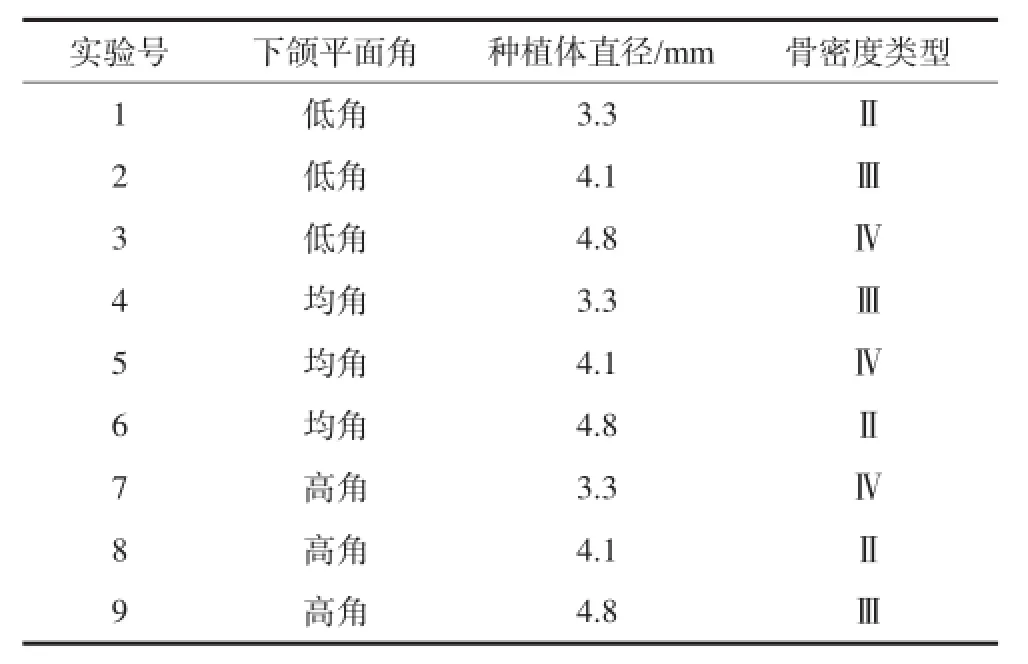
表 2 应力分布有限元分析的正交实验表Tab 2 The orthogonal experimental research of finite elemental analysis of stress distribution

1.2.3 建立有限元计算机模型 先用Pro/E建立直径为3.3、4.1、4.8 mm种植体计算机模型；再模拟Ⅱ、Ⅲ、Ⅳ类下颌骨结构和密度建模，得到3种牙槽骨计算机模型[1]；按照正交实验设计将种植体计算机模型植入牙槽骨计算机模型，得到9个种植复合体计算机模型。运用Pro/E Wildfire5.0中Mechanica模块对种植复合体计算机模型进行网格划分、定义材料特性、约束边界条件（约束形式定义为不可移动），得到约束边界条件后的种植复合体计算机模型（图2）。

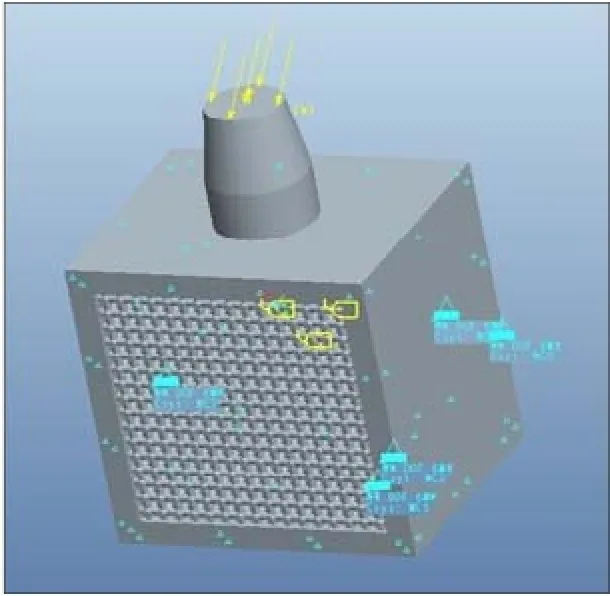
图 2 约束边界条件后的种植复合体计算机模型Fig 2 The computer model of dental implant with boundary restriction

1.2.4 加载方式 对种植复合体的受力状态进行理论分析，确定其受力作用面为种植复合体的面，受力大小为500 N[3]（图2中箭头所示）。对种植复合体采用3种角度进行加载，以模拟3种下颌平面角对种植体的应力分布影响。

1.2.5 观测部位 种植体颈部存在应力集中区域[4]，因此观测部位分别在种植复合体计算机模型颈部的近中（点1）、颊侧（点2）、舌侧（点3）、远中（点4），用Mechanica分析处理器对9个种植复合体计算机模型行静态受力分析，得到各观测点的应力值。

1.2.6 分析方法 采用极差法对有限元分析结果进行数据分析，分别计算各点应力值的T值、μ值和R值。T表示同一因素相同水平所对应的实验值之和。µ表示T的平均值，反映该因素各个水平对种植体应力影响的大小，且可以确定各个因素之间的最佳水平组合（纵向3个µ值相比数值低为最佳），临床中即可反映该部位种植体的相对最佳设计方案。R表示同一因素各个水平µ值之差的最大值，即极差，反映各个因素对种植体压应力影响程度的大小，可确定各因素之间的主次关系（横向3个R值相比数值高影响程度大），即临床中各因素的重要程度排序。

2 结果

2.1 数据采集

点1、2、3、4的应力值测量结果见表3。

2.2 有限元数据分析结果

各点T值、µ值、R值的测量结果见表4～7。点1位置各个因素最佳组合为：低角，4.8 mm，Ⅱ型骨；点1位置各因素主次关系依次为种植体直径、下颌平面角角度、骨密度。点2位置各个因素最佳组合为：低角，4.8 mm，Ⅱ型骨；点2位置各因素主次关系依次为种植体直径、骨密度、下颌平面角角度。点3位置各个因素最佳组合为：均角，4.8 mm，Ⅲ型骨；点3位置各因素主次关系依次为种植体直径、下颌平面角角度、骨密度。点4位置各个因素最佳组合为：低角，4.8 mm，Ⅱ型骨；点4位置各因素主次关系依次为种植体直径、下颌平面角角度、骨密度。综合分析4个点位的结果，得出最优参数组合为：低角，4.8 mm，Ⅱ型骨；各个因素的主次关系依次为种植体直径、下颌平面角角度、骨密度。

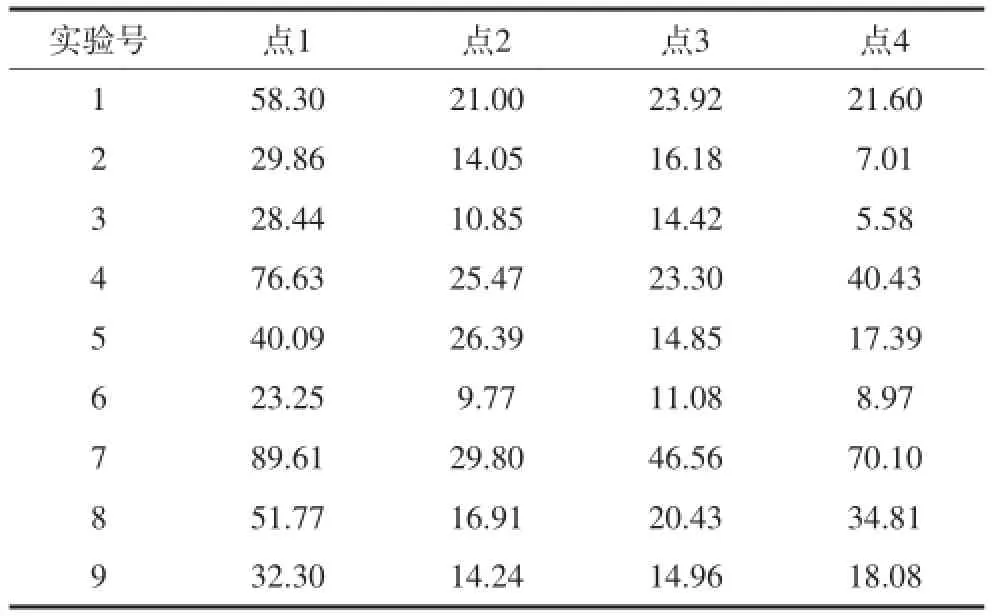
表 3 观测部位应力测量结果Tab 3 Data of stress of observation spot MPa

表 4 点1位置的T值、µ值和R值Tab 4 Data of T， µ， R at Spot 1 MPa

表 5 点2位置的T值、µ值和R值Tab 5 Data of T， µ， R at Spot 2 MPa

表 6 点3位置的T值、µ值和R值Tab 6 Data of T， µ， R at Spot 3 MPa

表 7 点4位置的T值、µ值和R值Tab 7 Data of T， µ， R at Spot 4 MPa

3 讨论

有限元法可以模拟形态结构复杂的牙体牙周组织以及种植体的空间几何形状、复杂的空间载荷情况和材料力学性能，能够比较精确地计算出各单元的应力、应变和位移，因此在本研究中运用有限元分析方法可以真实地模拟口腔受力环境，得出不同下颌平面角角度下种植体的应力分布情况[5]。

力学实验中存在因素的交互作用，正交实验是安排多因素实验、寻求最优水平组合的一种高效率分析设计方法。在实验因素的全部水平组合中，挑选部分有代表性的水平组合进行实验，可了解全面实验的情况，并找出最优的水平组合，因此本文采用正交实验方法。

3.1 下颌平面角对种植体应力分布的影响

下颌平面角是下颌平面与眶耳平面的交角，代表下颌体的陡度。下颌平面角平均角度为27.3[6]，小于22为低角，大于32为高角[7]。本实验分别选取14°、22°、34°作为低角、均角、高角的代表。从实验结果中可见，在同样的咬合力下，高角种植复合体所受应力最大，其次是均角复合体，低角复合体最小。在下颌平面角角度相同的情况下，直径较大的种植复合体所受应力最小。因此，在临床中，对于下颌平面角为均角和低角的患者，其磨牙区的种植体在直径选择上可适当宽松些，且可选择轴向位置植入；而对于高角患者，一方面在牙槽骨密度和宽度允许的情况下尽量选择直径较粗的种植体，或通过植骨的方法增加骨量而植入直径较粗的种植体，另一方面应考虑增加种植体的数量来降低单个种植体咀嚼时所产生的咬合分力，或采用正颌外科的方法矫正倾斜的牙槽骨，以满足种植体植入方向的需要[8]。

3.2 下颌骨骨密度对种植体应力分布的影响

根据Lekhollm和Zarb骨密度分类[8]，将骨质量分为4类。第Ⅰ类：几乎由均匀的密质骨构成；第Ⅱ类：较厚的皮质骨包绕密集排列的骨小梁；第Ⅲ类：薄层皮质骨包绕密集排列的骨小梁；第Ⅳ类：薄层皮质骨包绕疏松排列的骨小梁。临床上Ⅰ类骨所占比例极少，故本实验选取Ⅱ、Ⅲ、Ⅳ类骨作为实验对象。在所有贴片测得的应力中，除点位3外，其他点位Ⅱ类骨所受的应力以及最终的变形均为最小，因此在临床实际中，应尽可能选择骨密度较大的患者（Ⅱ类），对于骨密度较低患者应采用骨挤压技术，以提高种植窝内壁的牙槽骨密度，增加骨和种植体的接触面积，提高种植体的初期稳定性。

3.3 种植体规格对应力分布的影响

增加种植体的长度和直径可增加种植体与骨的接触面积、增强稳定性。种植体长度每增加3.0 mm，表面积可增加10%；而种植体（直径3.3 mm以上）直径每增加0.25 mm，表面积就可增加10%[8]。本实验对象为下颌第一磨牙，受下颌神经管解剖因素制约，不能过分增加种植体的长度，故只对种植体的直径进行研究。实验分析可得，种植体直径越大，应力越小，因此在临床中，根据实际缺牙间隙大小、在牙槽骨宽度允许的范围内，应选择直径较大的种植体，如宽度不能满足临床需要时，可采用骨劈开技术和/或骨移植技术增加牙槽骨宽度。

综上分析，下颌平面角角度对于种植体成功率有一定影响，角度越大稳定性越差；但有限元分析的结果对临床应用的指导作用有待进一步探讨。

[1] Lekholm U. Surgical considerations and possible shortcomings of host sites[J]. J Prosthet Dent, 1998, 79(1):43-48.

[2] 方开泰. 正交与均匀实验设计[M]. 北京: 科学出版社, 2001:85-90.

Fang KT. Orthogonal and uniform experimental design[M]. Beijing: Science Press, 2001:85-90.

[3] 王晓洁, 罗教明, 杨立, 等. 种植体周围骨内应力分布的三维有限元分析[J]. 实用口腔医学杂志, 2005, 21(5):592-596.

Wang XJ, Luo JM, Yang L, et al. Stress distribution in bone around dental implants studied by three-dimensional finite element analysis[J]. J Pract Stomatol, 2005, 21(5):592-596.

[4] 王晓洁, 罗教明, 陈继镛, 等. 下颌第一磨牙种植体周围应力三维有限元分析[J]. 华西口腔医学杂志, 2005, 23(2): 167-169.

Wang XJ, Luo JM, Chen JY, et al. The study on three-dimension finite element analysis of the stress distribution in the mandible bone around dental implants[J]. West Chin J Stomatol, 2005, 23(2):167-169.

[5] Rocha EP, Anchieta RB, Freitas AC Jr, et al. Mechanical behavior of ceramic veneer in zirconia-based restorations: a 3-dimensional finite element analysis using microcomputed tomography data[J]. J Prosthet Dent, 2011, 105(1): 14-20.

[6] 曾祥龙. 现代口腔正畸学诊疗手册[M]. 北京: 北京医科大学出版社, 2000:65-66.

Zeng XL. Modern orthodontics treatment manual[M]. Beijing: Beijing Medical University Press, 2000:65-66.

[7] 张君孝, 乔鸣芳. 280例正畸初诊患者下颌平面角观察研究[J]. 现代口腔医学杂志, 2008, 22(2):161-163.

Zhang JX, Qiao MF. A study on MP plane of 280 orthodontic patients[J]. J Modern Stomatol, 2008, 22(2):161-163.

[8] 宿玉成. 现代口腔种植学[M]. 北京: 人民卫生出版社, 2004:46, 96-97.

Su YC. Contemporary oral implantology[M]. Beijing: People’s Medical Publishing House, 2004:46, 96-97.

（本文编辑 杜冰）

Finite elemental analysis of the influence of mandibular plane angle on the stress distribution of implant tooth

Xing Weibin1, Zheng Shuxian2, Yang Shiyi1.
(1. Dept. of Stomatology, Tianjin Public Security Hospital, Tianjin 300042, China; 2. School of Mechanical Engineering, Tianjin University, Tianjin 300042, China)

Supported by: Tianjin Municipal Public Security Bureau of Science and Technology Funding for Projects (2012KYSGAY022). Correspondence: Yang Shiyi, E-mail: yangshiyi1982@126.com.

Objective Finite elemental analysis of the mechanical characteristics of a first mandibular implant molar under different mandibular plane angles determines the load conditions on the implant, thereby providing guidance for clinical application. Methods CT data of three mandibular plane angles (low, average, high) were collected. A finite elemental combination model of a dental implant was constructed. The orthogonal experimental research was designed. Results followed data collection and analysis. Results The optimal combination was a low angle, 4.8 mm, and type Ⅱ bone. The relations among diameter of the implant, angle of mandibular bone, and bone density were determined. Conclusion Mandibular plane angle influences the stability of a dental implant. Under constant biting force, dental implants bear the stress proportional to the angle, high angles cause high stress, average angles cause average stress, and low angles cause the least stress.

mandibular plane angle; dental implant; stress distribution; finite elemental analysis

R 783

A [doi] 10.7518/hxkq.2016.05.014

2016-03-05；

2016-07-10

天津市公安局科技资金（2012KYSGAY022）

邢维斌，副主任医师，学士，E-mail：xingweibin1967@ 163.com

杨适宜，主治医师，学士，E-mail：yangshiyi1982@126. com