配筋率对空心桥墩的抗震性能影响分析

张　标

(山西建筑工程(集团)总公司，山西 太原　030001)



配筋率对空心桥墩的抗震性能影响分析

张标

(山西建筑工程(集团)总公司，山西 太原030001)

采用ABAQUS有限元软件，建立了10个不同配筋率的桥墩模型，进行了弹塑性时程分析，得到了桥墩振动特性、墩顶位移时程曲线及墩底剪力时程曲线，并比较分析了不同模型在地震动作用下的抗震性能，确定了纵筋率、配箍率等参数对桥墩抗震性能的影响规律。

桥墩，配筋率，抗震性能，地震波

0　引言

目前，我国桥梁工程发展迅速，为节约建设成本，钢筋混凝土空心桥墩得到了广泛应用，所以对空心桥墩的抗震性能的研究也越来越迫切。因此，在抗震设计中如何改善空心桥墩的抗震性能是当前迫切需要解决的问题[1,2]。本文中采用通用有限元软件ABAQUS，建立了10个不同配筋率的桥墩模型，进行弹塑性时程分析。

1　模型概况

1.1基本模型参数的选取

结合工程设计实际，尺寸比例为1∶8桥墩缩尺模型，具体尺寸为：桥墩外围尺寸0.6 m×0.4 m，内围尺寸0.35 m×0.15 m(见图1)，墩高3 m，混凝土强度等级C30，钢筋强度HRB235。建立10个一致多尺度模型，分为两组，如表1所示。

表1　模型参数

1.2阻尼系数的确定

为计算方便，进行弹塑性时程分析，常假定阻尼为瑞利阻尼，瑞利阻尼矩阵[C]通过刚度矩阵与质量矩阵线性组合得到[4]：

[C]=α[M]+β[K]

(1)

其中，[M]为质量矩阵；[K]为刚度矩阵；α，β为瑞利阻尼系数，分别为质量系数、刚度系数。

1.3多尺度模型的建立

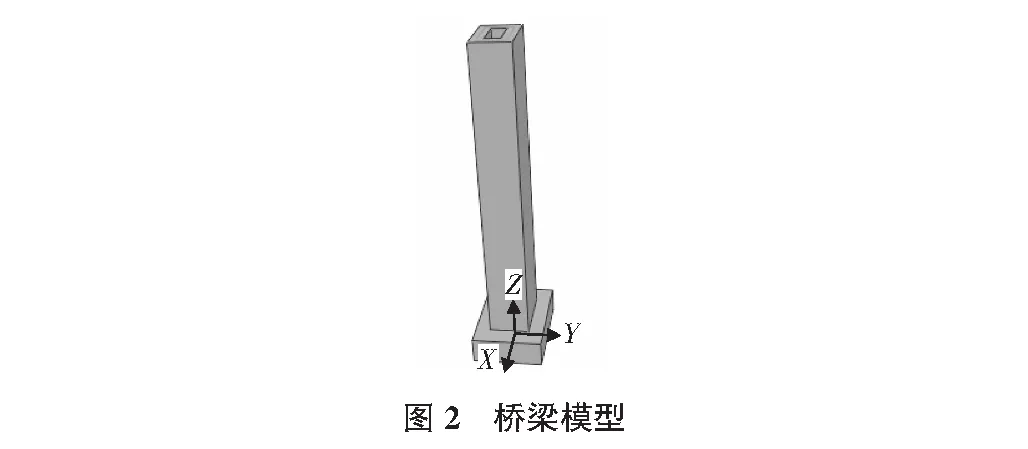
采用通用有限元软件ABAQUS，建立空心桥墩模型，在桥墩底部施加地震波。钢筋材料采用T3D2两结点三维线性桁架单元的理想弹塑性本构模型，网格采用Structured技术进行划分。建立的桥墩模型如图2所示。

2　动力时程分析

2.1弹塑性时程分析法的基本内容

地震作用下，桥墩体系的动力运动方程[3]：

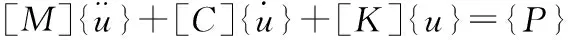
(2)

这里使用直接积分法，基本原理可以参考相关文献[7]。

2.2地震波的选取

地震不同将导致内力、位移等数据相差很大[5,6]。因此，选择合适的地震波是一重要工作。地震动强度通常可由加速度峰值(PGA)、速度峰值(PGV)、位移峰值 (PGD)体现。另外还要适当调整地震波的峰值，以便得到的地震记录的加速度峰值与地震烈度的统计加速度峰值相等，即：

(3)

其中，A(t)为调整后的地震波；Amax为相应烈度下统计得到的加速度峰值；αmax为所选地震波记录的加速度峰值；α(t)为选择的地震波。

本文研究以地面的峰值加速度(PGA)为指标，地震波为EI Centro波，时间间隔为0.02 s，PGA为0.341 7g，时间总长为30 s，见图3。

3　结果与分析

3.1配筋率对桥梁振动特性的影响

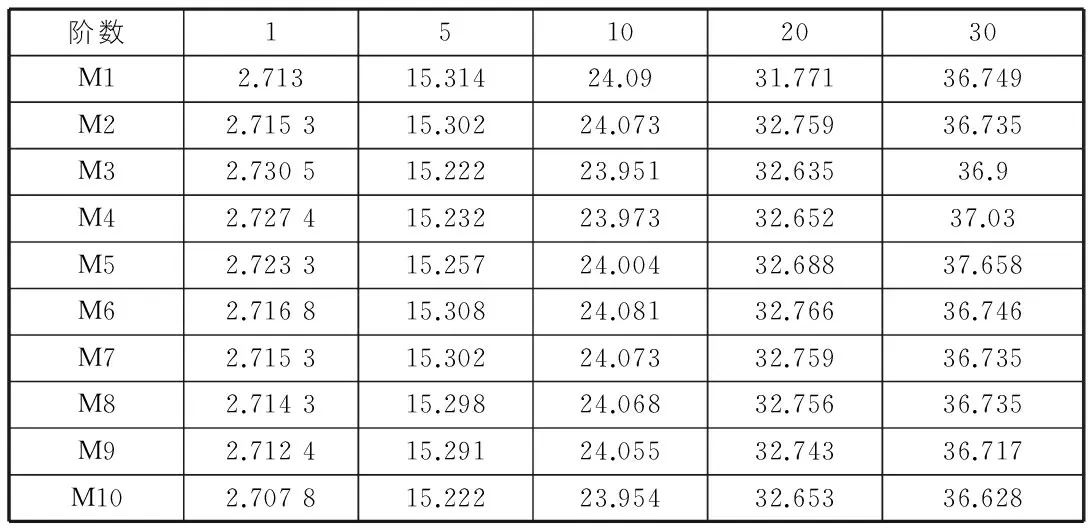
表2列出了桥墩在不同配筋率情况下的振动频率。

表2　各模型自振频率

阶数15102030M12.71315.31424.0931.77136.749M22.715315.30224.07332.75936.735M32.730515.22223.95132.63536.9M42.727415.23223.97332.65237.03M52.723315.25724.00432.68837.658M62.716815.30824.08132.76636.746M72.715315.30224.07332.75936.735M82.714315.29824.06832.75636.735M92.712415.29124.05532.74336.717M102.707815.22223.95432.65336.628

表2列出了不同纵筋率(M1～M5模型)和配箍率(M6～M10模型)的自振频率。表2表示振动阶数较低时，纵筋率和配箍率对频率影响不大，主要表现桥墩的柔性。当阶数较高时，增大模型纵筋率振动频率增大，但振幅不大，这是由于总体而言模型配筋较少，对桥墩结构刚度影响较小。配箍率对桥墩的振动频率影响不大。

3.2位移响应和剪力响应

图4～图7比较了不同配筋率情况下的墩顶位移曲线、墩底剪力曲线。

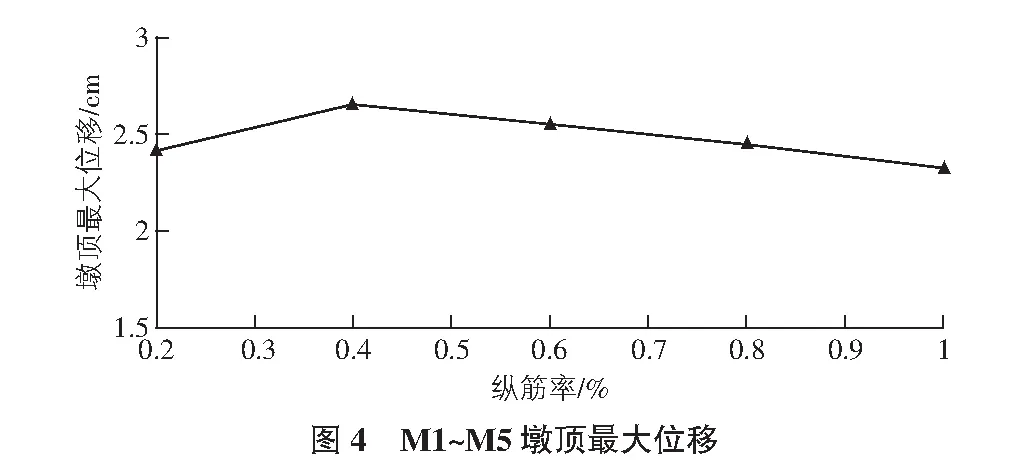
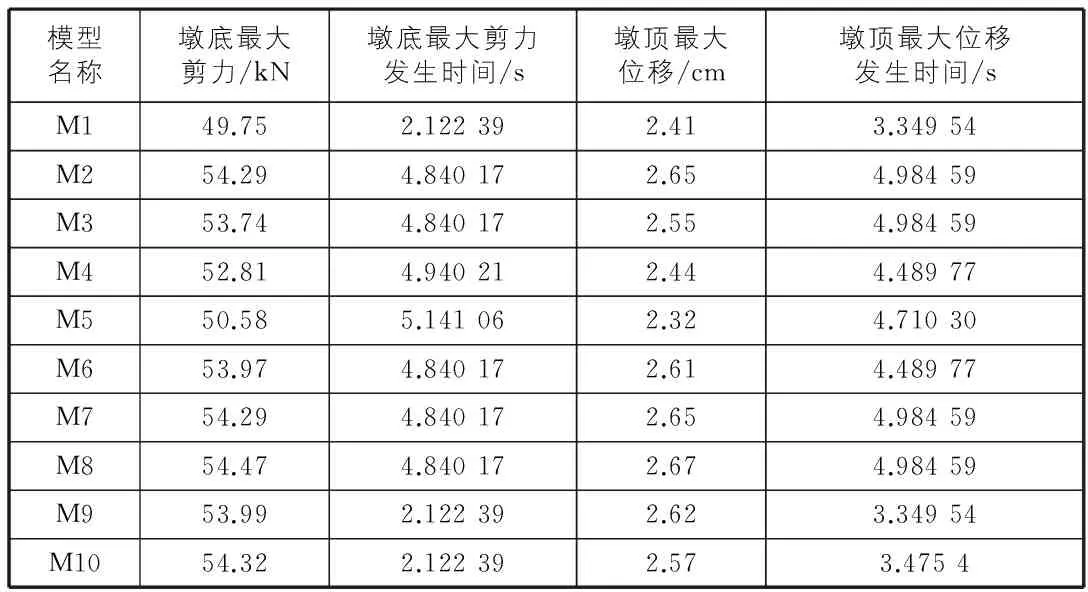
表3　动力时程分析响应结果

模型名称墩底最大剪力/kN墩底最大剪力发生时间/s墩顶最大位移/cm墩顶最大位移发生时间/sM149.752.122392.413.34954M254.294.840172.654.98459M353.744.840172.554.98459M452.814.940212.444.48977M550.585.141062.324.71030M653.974.840172.614.48977M754.294.840172.654.98459M854.474.840172.674.98459M953.992.122392.623.34954M1054.322.122392.573.4754

从表3和图4得出，配箍率保持一定时，纵筋率的增加会增大桥墩刚度，并总体减小模型墩顶位移。各模型墩顶最大相对位移发生时间离散性较大，且迟于地震波峰值时间，体现了响应的滞后性。由表3和图5可以看出，当纵向配筋率较小时，随着纵筋率的提高，墩底最大剪力值有所增加，桥墩构件的塑性破坏程度减小，但随着配筋率的增大，墩底混凝土先于钢筋破坏导致超筋破坏，桥墩构件的塑性破坏程度有所增大，墩底最大剪力反而下降。各模型墩底最大剪力发生时间离散性较大，并且迟于地震波峰值的时间，体现了响应的滞后性。对比不同模型的滞回曲线，增加纵筋率，滞回曲线面积明显增大，耗能能力显著提升。

由表3和图6可知，在地震动作用下，保持纵筋率0.4%不变,箍筋间距由0.1 m增到0.5 m时，M6～M10模型墩顶位移变化不大，表明配箍率对墩顶位移响应影响较小，各模型墩顶最大相对位移发生时间与上述的一致。根据表3和图7得到，在地震动作用下，纵筋率固定提高配筋率时，虽墩底最大剪力有一定变化，但总在一定值附近波动，变化不大，说明配箍率对墩底剪力大小影响较小，对比不同模型的滞回曲线，增加配箍率，滞回曲线面积基本不变，对耗能能力影响较小。

4　结语

1)随着纵向钢筋配筋率的提高，墩顶最大位移呈减小趋势，但配筋率较小时，墩底最大剪力随着配筋率的继续增大而增大，但当配筋率继续增大时，墩底最大剪力反而下降，基于经济考虑配筋率不宜太大。

2)增加桥墩配箍率，墩顶最大位移变化较小，墩底最大剪力有一定波动，总体来说配箍率对桥梁结构的耗能能力影响不大。

3)桥墩顶最大相对位移发生时间离散性较大，并且迟于地震波峰值的时间，体现了响应的滞后性。

[1]AUGUST F Z.Design of reinforced concrete bridge columns for strength and ductility[D].New Zealand:The University of Canterbury,Christchurch,1985.

[2]陈惠发，段炼.桥梁工程抗震设计[M].北京:机械工业出版社，2008.

[3]R.W.Clough,J.Penzien.Dynamics of structures[M].Berkeley:Computers and Structures Inc.,1975:169-173.

[4]邹德高,徐斌.瑞利阻尼系数确定方法对高土石坝的地震响应影响分析[J].岩土力学,2011,32(3):797-803.

[5]任森智.多维地震动作用下框架结构的地震反应分析[J].工程抗震与加固改造,2010,32(2):16-19.

[6]王玉镯，傅传国.ABAQUS结构工程分析及实例讲解[M].北京：中国建筑工业出版社，2010.

[7]杜轲,孙景江,丁宝荣,等.显式分析方法在高层建筑弹塑性地震反应分析中的适用性研究[J].地震工程与工程振动,2015(4):85-93.

On influence of reinforcement percentage on seismic performance of hollow piers

Zhang Biao

(ShanxiArchitecturalEngineering(Group)Corporation,Taiyuan030001,China)

The paper adopts ABAQUS finite element software, establishes the bridge models with various reinforcement percentage, undertakes the elastic-plastic time-history analysis, concludes the pier vibration features, time-history curve of the pier top displacement, and time-history curve of the pier bottom shearing, compares the seismic performance under the earthquake effect, and identifies the parameter including the longitudinal reinforcement ratio and reinforcement percentage on the seismic performance of the bridge piers.

bridge pier, reinforcement percentage, seismic performance, seismic wave

1009-6825(2016)23-0186-03

2016-06-01

张标(1987- )，男，硕士

U441.3

A