区间梯形模糊软集及其相关性质
朱 捷,徐 源,陈孝国
(黑龙江科技大学 理学院,哈尔滨 150022)
区间梯形模糊软集及其相关性质
朱捷,徐源,陈孝国
(黑龙江科技大学 理学院,哈尔滨 150022)
为进一步丰富模糊软集扩展理论,提出了区间梯形模糊软集的定义,并给出交、并、补等运算性质,得到结合律、分配律、对偶律等相关定理并给出证明。该研究成果对区间梯形模糊软集理论完善和实际应用起到一定的促进作用。
软集; 区间梯形模糊数; 区间梯形模糊软集
0 引 言
随着社会不断发展,许多工程问题变得越来越复杂,影响因素众多、数据量较大,常用的处理方法概率论[1]、区间数理论[2]、模糊理论[3]和粗糙集理论[4]都无法得到满意的结果。为此,Molodtsov D[5]在1999年针对不确定性问题提出了软集概念。软集具有参数化更加灵活,能够细腻地描述客观事物的不确定性等优势,所以软集被提出后迅速受到众多学者的广泛关注,Majumdar等[6]提出了软集的相似度概念。Ali等[7]研究了软集的限制交集及限制并集。毛军军等[8]利用衰减函数定义了时序模糊软集。在软集扩展方面,Maji等[9]将模糊集与软集相结合提出模糊软集理论。Kuang等[10-11]将三角模糊数、梯形模糊数与软集相结合提出了三角模糊软集和梯形模糊软集。陈孝国等[12]在上述研究基础上提出了区间三角模糊软集的概念,并讨论了AND、OR等相关运算及性质。
虽然软集的扩展研究取得了丰硕成果,但是对区间梯形模糊软集的研究相对较少,且文献[12]提出的定理在运算上较为复杂,需要进一步改进。因此,笔者提出区间梯形模糊软集的概念,并探讨区间梯形模糊软集的运算性质和相关定理,以期丰富模糊软集理论。
1 区间梯形模糊数及其性质

如果0 定义2设s=[(a-,a+);b;c;(d-,d+)]和t=[(m-,m+);h;k;(g-,g+)]是两个区间梯形模糊数,如果a-≤m-,a+≤m+,b≤h,c≤k,d-≤g-,d+≤g+,则称s≤t。 定义3设s=[(a-,a+);b;c;(d-,d+)]和t=[(m-,m+);h;k;(g-,g+)]是两个区间梯形模糊数,则 s∩t=[(min(a-,m-),min(a+,m+));min(b,h);min(c,k);(min(d-,g-),min(d+,g+))], s∪t=[(max(a-,m-),max(a+,m+));max(b,h);max(c,k);(max(d-,g-),max(d+,g+))]。 定义4设t=[(m-,m+);h;k;(g-,g+)]是一区间梯形模糊数,则t的补集为 tc=[(1-g+,1-g-);1-k;1-h; (1-m+,1-m-)] 。 定义5设s=[(a-,a+);b;c;(d-,d+)]和t=[(m-,m+);h;k;(g-,g+)]是两个区间梯形模糊数,常数k>0,则 s+t=[(a-+m--a-m-,a++m+-a+m+); b+h-bh;c+k-ck;(d-+g-- d-g-,d++g+-d+g+)], ks=[(1-(1-a-)k,1-(1-a+)k);1-(1-b)k;1-(1-c)k;(1-(1-d-)k,1-(1-d+)k)]。 定义3至定义5能够保证规范区间梯形模糊数运算的封闭性。 定义6设U为论域,E为参数集,Г(U)表示论域U上所有区间梯形模糊集,A⊆E称(F,A)为论域U上的一个区间梯形模糊软集,其中映射F:A→Г(U)。即对∀e∈A,有 F(e)={〈x,sF(e)(x)〉|x∈U}, 式中,SF(e)是F(e)中x所对应的区间梯形模糊数。 定义7假设(F,A)和(G,B)是定义在论域U上的区间梯形模糊软集,说(F,A)∩(G,B)=(H,C)为这两个集合的交集,而且(F,A)∩(G,B)=(H,C),这里C=A∩B 。对于∀ε∈C,有 H(ξ)=F(ξ)∩G(ξ)={〈x,sF(ξ)(x)∩ sG(ξ)(x)〉|x∈U}, sF(ε)(x)和sG(ε)(x)分别是F(ε)和G(ε)中x所对应的区间梯形模糊数。 定义 8设(F,A)和(G,B)为论域U上的两个区间梯形模糊软集,有(F,A)∪(G,B)是这两个集合的并集,而(F,A)∪(G,B)=(M,D),这里D=A∪B。对于∀ε∈D,有 M(ε)=F(ε)∪G(ε)={〈x,sM(ε)(x)〉|x∈U}, 这里, 其中,sF(ε)(x)和sG(ε)(x)分别为F(ε)和G(ε)中x所对应的区间梯形模糊数。 定理1设(F,A)和(G,B)是论域U上的区间梯形模糊软集,有 (1)((F,A)∪(G,B))c=(F,A)c∩(G,B)c, (2)((F,A)∩(G,B))c=(F,A)c∪(G,B)c。 证明(1)和(2)的证明过程相似,所以只证(1)。假设 (F,A)∪(G,B)=(M,D), 这里 ((F,A)∪(G,B))c=(M,D)c=(Mc,D), 而 (F,A)c∩(G,B)c=(Fc,A)∩(Gc,B)=(H,C)。 对于∀ε∈D,有 Mc(ε)=(M(ε))c=({〈x,sM(ε)(x)〉|x∈U})c= Fc(ε)∩Gc(ε)=H(ε)。 所以, ((F,A)∪(G,B))c=(F,A)c∩(G,B)c 成立。 定理2设((F,A)∪(G,B))c=(F,A)c∩(G,B)c(F,A),(G,B)和(L,C)为论域U上的两个区间梯形模糊软集,然后有: (1)((F,A)∪(G,B))∪(L,C)=(F,A)∪((G,B)∪(L,C)), (2)((F,A)∩(G,B))∩(L,C)=(F,A)∩((G,B)∩(L,C))。 证明(1)和(2)的证明过程类似,所以只证(1)。假设 (F,A)∪(G,B)=(M1,D1), (M1,D1)∪(L,C)=(M2,D2), (G,B)∪(L,C)=(M3,D3), (F,A)∪(M3,D3)=(M4,D4)。 这里D2=D4=A∪B∪C。对于∀ε∈D1,有 M1(ε)={〈x,sM1(ε)(x)〉|x∈U}, 对于∀ε∈D3,有 M3(ε)={〈x,sM3(ε)(x)〉|x∈U}, 对于∀ε∈D2,有 M2(ε)={〈x,sM2(ε)(x)〉|x∈U}, 对于∀ε∈D4,有 M4(ε)={〈x,sM4(ε)(x)〉|x∈U}, 从以上运算规则中,得到 sM2(ε)(x)=sM4(ε)(x)。 所以, ((F,A)∪(G,B))∪(L,C)=(F,A)∪((G,B)∪(L,C))成立。 定理3假设(F,A),(G,B)和(L,C)为论域U上的区间梯形模糊软集,有 (1)((F,A)∪(G,B))∩(L,C)=((F,A)∩(L,C)∪((G,B)∩(L,C)), (2)((F,A)∩(G,B))∪(L,C)=((F,A)∪(L,C)∩((G,B)∪(L,C))。 证明只需证明(1),因为(1)和(2)证明过程类似。假设 (F,A)∪(G,B)=(M1,D1), (M1,D1)∩(L,C)=(H1,D2), (F,A)∩(L,C)=(H2,D3), (G,B)∩(L,C)=(H3,D4), (H2,D3)∪(H3,D4)=(M2,D5)。 显然,D2=D5=(A∪B)∩C。对于∀ε∈D1,有: M1(ε)={〈x,sM1(ε)(x)〉|x∈U}, 对于∀ε∈D2,有: H1(ε)={〈x,sH1(ε)(x)〉|x∈U}= {〈x,sM1(ε)(x)∩sL(ε)(x)〉|x∈U},sH1(ε)(x)= 对于∀ε∈D3,有 H2(ε)={〈x,sH2(ε)(x)〉|x∈U}= {〈x,sF(ε)(x)∩sL(ε)(x)〉|x∈U}。 对于∀ε∈D4,有 H3(ε)={〈x,sH3(ε)(x)〉|x∈U}= {〈x,sG(ε)(x)∩sL(ε)(x)〉|x∈U}。 对于∀ε∈D5,有: M2(ε)={〈x,sM2(ε)(x)〉|x∈U}, 从而, sH1(ε)(x)=sM2(ε)(x)。 所以, ((F,A)∪(G,B))∩(L,C)=((F,A)∩ (L,C)))∪((G,B)∩(L,C)) 成立。 在模糊软集、梯形模糊软集和区间三角模糊软集的研究基础上,给出了区间梯形模糊软集的定义和交、并、补等运算性质,并探讨了结合律、分配律、对偶律等相关定理,给出证明过程。所得研究成果进一步扩展了模糊软集理论,也为解决参数值以区间梯形模糊数形式出现的不确定性决策问题提供理论依据和解决方法。 [1]缪柏其,胡太忠.概率论教程[M].合肥:中国科学技术大学出版社,2009:1-15. [2]ZHANG S F,LIU S Y,ZHAI R H.An extended GRA method for MCDM with interval-valued triangular fuzzy assessments and unknown weights[J].Computers &Industrial Engineering,2011,61(4):1336-1341. [3]ZADEH I A.Fuzzy sets[J].Information and Control,1965,8(3):338-353. [4]PAWLAK Z.Rough sets[J].International Journal of Computer and Information,Sciences,1982,11:341-356. [5]MOLODTSOV D.Soft set theory—first results[J].Computers and Mathematics with Applications,1999,37(415):19-31. [6]MAJUMDAR P,SAMANTA S K.Generalised fuzzy soft sets[J].Computers and Mathematics with Applications,2010,59(4):1425-1432. [7]AlI M I.A note on soft sets,rough soft sets and fuzzy soft sets [J].Applied Soft Computing,2011,11(4):3329-3332. [8]毛军军,姚登宝,王翠翠,等.基于时序模糊软集的群决策方法[J].系统工程理论与实践,2014,34(1):182-189. [9]MAJI P K,BISWAS R,ROY A R.Fuzzy soft sets[J].Journal Fuzzy Mathematics,2001,9(3):589-602. [10]KUANG T,XIAO Z.A multi-criteria decision making approach based on triangle-valued fuzzy soft sets[J].Journal of Convergence Information Technology,2012,7(15):17-25. [11]KUANG T.Trapezoid-valued fuzzy soft sets and its applications[J].Advances in Information Sciences and Service Sciences,2012,4(15):310-316. [12]陈孝国,杜红.区间三角模糊软集及其动态决策方法[J].系统工程与电子技术,2015,37(5):1111-1115. (编辑王冬) Interval-valued trapezoid fuzzy soft set and its properties ZHU Jie,XU Yuan,CHEN Xiaoguo (School of Sciences,Heilongjiang University of Science &Technology,Harbin 150022,China) This paper is an effort to improve the extension study of the fuzzy soft set theory.The study produces the definition of the interval-valued trapezoid fuzzy soft;the operation properties of their intersection union and complementary set;and the relative theorem of its associative law,distributive law,dual law and the proofs.The results could contribute to promote the better application of the interval-valued trapezoid fuzzy soft set theory. fuzzy soft set;interval-valued trapezoid fuzzy figures;interval-valued trapezoid fuzzy soft set 2016-04-28 黑龙江省自然科学基金项目(QC2015055);黑龙江省教育厅科学技术研究项目(12531577);中国矿业大学(北京)博士研究生拔尖创新人才培育基金项目(20150606) 朱捷(1964-),女,浙江省宁波人,教授,博士,研究方向:统计应用,E-mail:zhujie6411@163.com。 10.3969/j.issn.2095-7262.2016.03.020 O159;C934 2095-7262(2016)03-0332-04 A2 区间梯形模糊软集及其性质
3 区间梯形模糊软集的相关定理
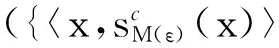

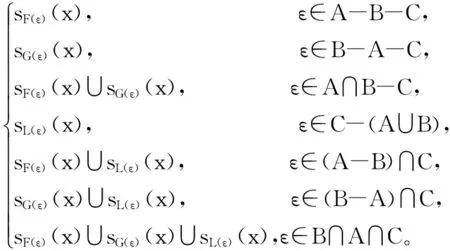


4 结束语

