基于XFEM研究含颗粒夹杂材料的疲劳裂纹行为

束一秀，李亚智，尚海江，姜　薇

(西北工业大学 航空学院，西安　710072)



基于XFEM研究含颗粒夹杂材料的疲劳裂纹行为

束一秀，李亚智，尚海江，姜薇

(西北工业大学 航空学院，西安710072)

材料中的颗粒夹杂会改变附近的应力分布，对疲劳裂纹的扩展行为有显著的影响。在XFEM方法的基础上，借助一种考虑界面影响的交互积分方法以及ABAQUS的二次开发环境，模拟疲劳裂纹在非匀质材料中的扩展，研究夹杂颗粒对疲劳裂纹扩展的影响模式。裂纹和夹杂使用扩充函数结合水平集函数隐式模拟，使用最大周向拉应力准则判断裂纹扩展方向。通过模拟疲劳裂纹经过对称夹杂和非对称夹杂的情况，分别研究夹杂对裂纹扩展速率以及扩展路径的影响模式，探讨了夹杂的材料性质对结果的影响，考虑了裂纹在特定情况下可能刺入夹杂的情况。将部分数值结果与更新网格方法以及以往的扩展有限元模拟结果进行了对比，体现了该文方法的优点和模拟结果的合理性。

疲劳裂纹扩展；扩展有限元法；交互积分；应力强度因子；材料界面

0　引言

如果材料内存在材料性质与母材不同的夹杂，不管这些夹杂是偶然存在(材料加工过程中的杂质)或是人为添加(颗粒增强复合材料)，都会显著地影响材料的力学性能，其中夹杂对裂纹扩展的影响是受关注的问题之一。由匀质材料形成的结构中，填充孔和空孔也可看作是夹杂问题的特殊形式。夹杂与裂纹之间的相互作用对于很多工程材料和结构的断裂以及疲劳寿命等问题具有重要的意义。

解决此类问题有很多种方法。一些学者[1-3]推导了夹杂对裂纹作用的解析解，证明夹杂对其附近的裂纹尖端有明显的“抑制”或“放大”作用。数值解法也被用来求解夹杂和裂纹的相互作用，比如有限元方法[4-5]和边界元方法[6-8]。扩展有限元方法[9-12](XFEM)是一种解决区域内包含不连续问题的数值方案，与传统有限元方法相比，其优点是不依赖于不连续体的几何形状，只要针对不同的间断类型选择不同的扩充函数，即可模拟域内包含裂纹和夹杂的问题，避免了网格更新。于红军、王志勇[13-14]使用扩展有限元方法结合一种考虑材料界面的交互积分形式计算了夹杂对裂尖能量释放率的影响，但他们没有使用裂尖扩充函数，而是通过调整裂尖处的网格来提高精度，其优点是求解不依赖于裂尖应力场的形式，缺点是需要对裂尖处的网格作特殊处理；Natarajan[15]使用扩展有限元法计算了裂尖前方的圆形夹杂对裂尖能量释放率的影响，但没有对受夹杂影响之后的裂纹扩展路径进行分析。虽然很多学者[7-8，14]模拟了裂纹受夹杂影响下的扩展路径分析，但没有考虑裂纹刺入夹杂的情况，而实际上如果夹杂的刚度小于母材，或者夹杂的材料虽然刚度大于母材但差距不大，不能视为刚性夹杂，在多个夹杂综合作用的情况下，有可能会出现裂纹刺入夹杂的情况。

本文基于扩展有限元方法研究母材中含颗粒夹杂的情况下疲劳裂纹的扩展行为。第一部分介绍了相关数值过程以及断裂参数的计算方法，数值计算的实现基于ABAQUS软件的二次开发；第二部分通过算例分析了规则分布的夹杂对Ⅰ型疲劳裂纹扩展寿命的影响并与更新网格法作对比；第三部分模拟了不同性质的夹杂对裂纹扩展路径的影响，探讨了裂纹经过夹杂区的扩展规律，分析了裂纹刺入夹杂时应力强度因子的变化规律。算例合理地反映了裂纹经过颗粒夹杂区域时的扩展行为。

1　数学模型

1.1扩展有限元离散形式

Belytschko[10]等提出了求解线弹性问题的扩展有限元方法，其核心思想是在标准位移场上增加附加位移场来模拟不连续问题。如果区域内包含裂纹和夹杂，则其位移函数可写成式(1)的形式：

(1)

式中Ni为形状函数；H为阶跃函数，表征被裂纹贯穿单元的节点的扩充函数，在裂纹两侧分别取1和-1；φ为表征夹杂的扩充函数[12]，其形式见式(2)；Ψj(r，θ)为裂尖扩充函数，其形式见式(3)。

(2)

式中ζi为节点到夹杂边界的符号距离函数。

(3)

单元刚度矩阵和节点力向量分别为式(4)和式(5)所示：

(4)

(5)

其中

(6)

式中B为几何矩阵；D为弹性矩阵。

1.2裂纹和夹杂的水平集表征

扩展有限元方法中的裂纹和夹杂不依赖于网格，用水平集方法来表征任意形式的裂纹[16-17]及颗粒夹杂[12]的几何形状。

裂纹属于非闭合曲线，需要使用2个水平集函数φ和ψ来确定其几何形状及位置(图1)。其中，φ用来表征裂纹面，ψ用来辅助确定裂尖位置，则一条任意位置及形状的裂纹可描述为φ=0，ψ≤0。

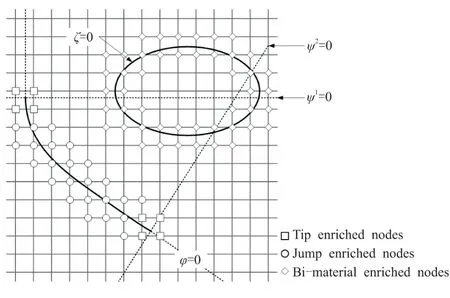
图1　扩充节点和水平集函数的零等值面

颗粒夹杂边界是封闭曲线，只需要用一个水平集函数ζ即可精确描述其几何形状，ζ=0即为夹杂的轮廓线。以图1中的椭圆形夹杂为例，节点的水平集函数可用式(7)计算：

(7)

2　疲劳裂纹扩展

2.1交互积分

文献[13]提出了一种考虑材料界面影响的交互积分形式：

(8)

现在考察如果裂纹与材料界面相交，交互积分是否依然满足式(8)的形式。如图2所示，积分区域被分割为A1、A2和A33个材料性质均匀的积分区域，定义3个区域的轮廓为Γ01、Γ02和Γ03，则交互积分形式可表示为式(9)的形式：

(9)

(10)

图2　裂纹穿过材料界面时的积分域

分别对式(9)中的3个环路积分使用散度定理，将线积分转换为面积分，则区域内的交互积分的形式为

(11)

(12)

2.2积分方案

对于裂纹或者材料界面相交的单元，由于单元内部的位移函数不连续，无法直接使用高斯积分，一种可行的方法是将单元分割成若干子单元，在每个子单元内位移函数连续可微，分别对子区域积分之后累加即可得到精确的单元积分。对于裂纹与材料界面穿过同一个单元的情况(图3)，视裂纹与材料界面的相对位置，将单元分为若干个区域，然后以区域内的形心、裂尖或交点为基准，将各区域划分为三角形子区域，再进行积分。对于混合单元，通过加密积分点提高计算精度，使用5×5高斯积分，对于划分之后的单元，试算之后发现，每个三角形子区域取3个积分点，已经能获得较高的精度，因此每个子区域分配3个高斯积分点。

图3　裂纹与材料界面经过同一个单元时的积分方案

2.3应力强度因子

交互积分与应力强度因子的关系为

(13)

(14)

式中Etip为裂尖所在位置的弹性模量；νtip为裂尖所在位置的泊松比。

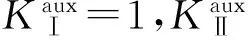
2.4裂纹扩展方向

判定裂纹扩展方向基于最大周向应力准则[19]，即寻找θc使该方向的剪应力为零，得到

(15)

3　 数值结果和分析

本文数值方法的实现基于ABAQUS软件的二次开发。其中，有限元方程的创建以及求解在ABAQUS环境下完成，前后处理(模型创建、裂纹及夹杂初始化、水平集更新、断裂参数计算以及节点应力计算等)使用FORTRAN编程实现，并通过ABAQUS子程序UEXTERNALAB进行数据交换，使用软件TECPLOT绘制结果云图。

3.1网格密度对精度的影响

为了验证网格密度对本文方法精度的影响，考虑图4(a)所示的边缘裂纹拉伸平板，裂纹长度a/L=0.2。使用四边形网格划分模型，交互积分区域半径取3倍单元特征长度。为了更真实地反应XFEM方法的精度，在水平和竖直方向分别划分奇数个单元，保证裂纹面贯穿单元，且裂尖位于单元内部。

3.2夹杂对疲劳裂纹扩展寿命的影响

考虑图4(b)所示的模型及加载方式，初始裂纹长度a=20 mm，在裂纹行进路线的两侧对称分布着一对圆形夹杂，研究夹杂材料、尺寸及位置对疲劳裂纹扩展寿命的影响。母板弹性模量为68 320 N/mm2，泊松比为0.3，使用101×151的四边形网格。

3.2.1夹杂-裂纹距离对裂纹扩展速率的影响

取夹杂半径R=5 mm，夹杂与母材的弹性模量比EⅠ/E=2，改变夹杂边缘之间的最短距离S，计算裂纹扩展曲线及速率。

图6是XFEM和FEM计算模型的网格划分对比。可看到，使用XFEM方法，时裂纹和夹杂是完全独立于网格的。

图7是无量纲能量释放率曲线。其中，G0是裂纹在不含夹杂材料中的能量释放率，裂纹扩展速率的变化正比于能量释放率的变化。从图7可见，夹杂性质不变的情况下，对裂纹扩展速率影响的程度与离裂纹路径的距离成反比。对于硬夹杂，受到前方夹杂的影响，裂纹扩展速率相比于匀质材料中降低了；当裂尖经过夹杂中心位置之后，裂纹扩展速率有小幅的提高，然后逐渐趋于在匀质材料中的扩展速率。注意到结果中没有给出S=5 mm时的更新网格方法的模拟结果，因为此时裂纹距离夹杂边缘太近，没有足够的空间划分裂尖奇异网格，S取10、15、20 mm时，XFEM模拟结果与更新网格法模拟结果相差极小。

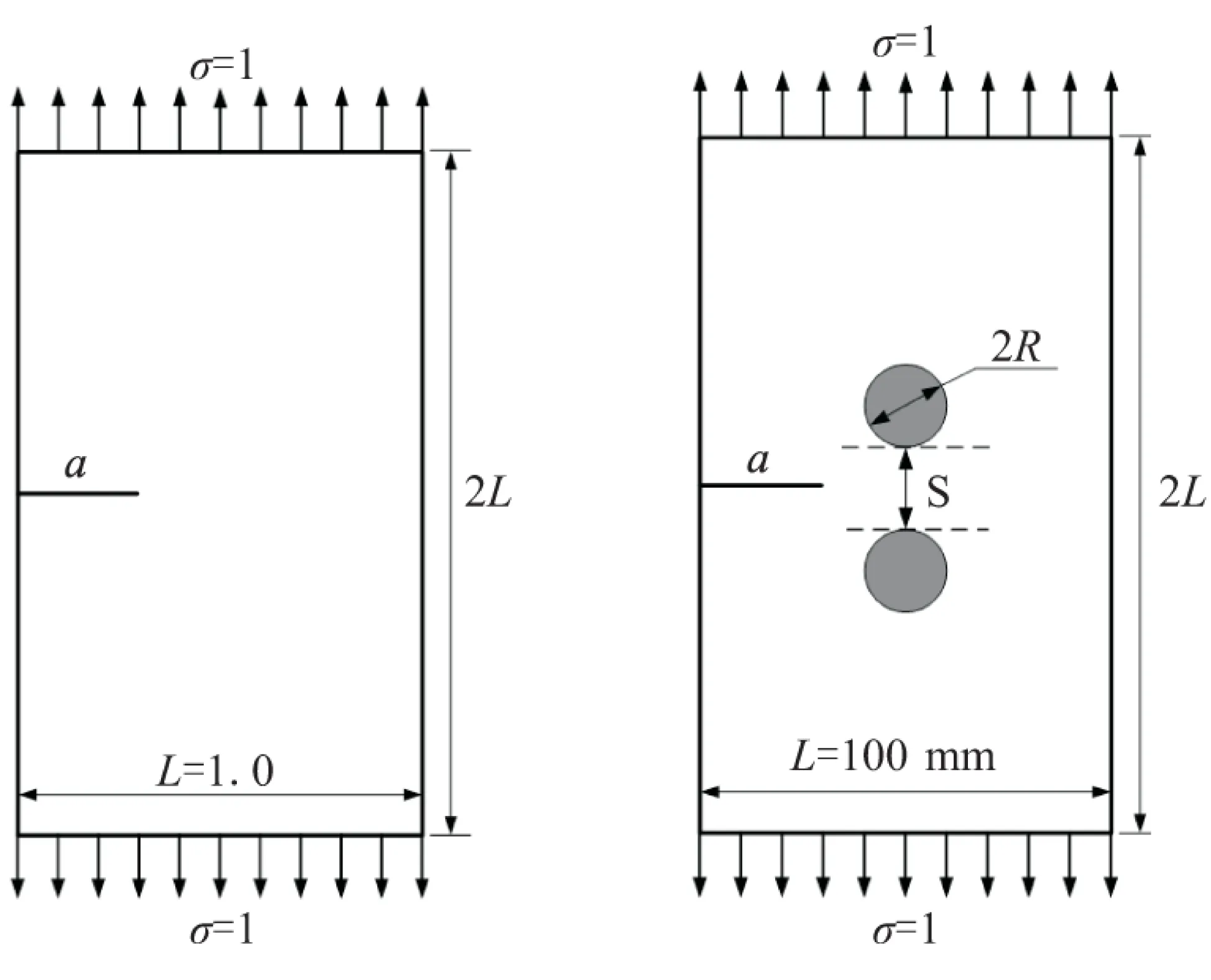
(a)均质平板　　　(b)含对称分布夹杂平板

图5　应力强度因子数值结果相对于节点数的收敛性

(a)XFEM　　　　　　　　(b)更新网格法

图7　不同S值下的裂纹扩展速率比

当S=5 mm，裂纹扩展到夹杂附近时，裂尖距离夹杂很近，此时积分域内将包含材料界面。图8是使用标准交互积分以及本文方法计算S=5 mm时，裂纹扩展过程中的无量纲能量释放率。从图8可看出，当积分域包含材料界面时，标准的交互积分方法计算的结果出现了很大的波动，而考虑了材料界面影响的交互积分能够得到合理的结果。

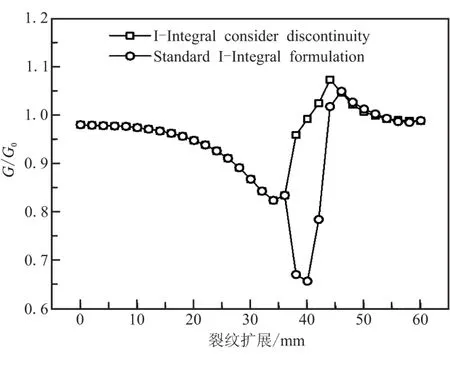
图8　交互积分方法对数值结果的影响

3.2.2夹杂材料对裂纹扩展速率的影响

除夹杂与裂纹的距离之外，夹杂对能量释放率的影响程度还与材料性质相关。图9为保持夹杂与裂纹距离不变的情况下，改变夹杂材料时裂尖无量纲能量释放率的变化。由图9可见，硬夹杂对裂纹扩展速率影响的严重程度与EⅠ/E的大小成正比；软夹杂对裂纹扩展速率的影响的作用规律与硬夹杂相反，裂纹首先加速扩展，在经过夹杂中心位置之后，又有小幅的减速；然后，逐渐趋于在匀质材料中的扩展速率，影响的严重程度与EⅠ/E的大小成反比。

从3.2节的模拟结果可发现，位于裂纹扩展路径两侧的夹杂会影响疲劳裂纹扩展速率，软夹杂对加速裂纹扩展，而硬夹杂会抑制疲劳裂纹扩展，影响程度与夹杂和母材的弹性模量比、半径以及到裂纹路径的距离有关。

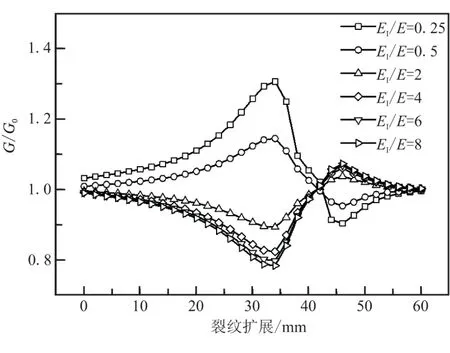
图9　不同EⅠ/E下的裂纹扩展速率比

3.3夹杂对裂纹扩展路径的影响

3.3.1裂纹经过单个夹杂

考察图10所示的方形平板(W=L=100 mm)，平板含一条边缘裂纹以及一个圆形夹杂。初始裂纹长度a0=30 mm，d=5 mm。分别取夹杂和板的弹性模量比EⅠ/E为2和0.5，取裂纹扩展步长为1 mm，计算裂纹扩展路径以及无量纲化的能量释放率G/G0，并与文献[14]的结果对比。

裂纹靠近夹杂时的扩展行为如图11所示。

图10　含夹杂边缘裂纹平板

从图11(b)可看出，大约x/r=-5～-6的位置开始，裂尖能量释放率受到了夹杂的影响，当裂纹扩展到x/r=-1的位置时，裂纹才开始偏离原来的扩展方向：硬夹杂迫使裂纹向偏离夹杂的方向扩展，软夹杂吸引裂纹向夹杂扩展；当裂纹越过夹杂中心点之后，夹杂对裂纹的影响逐渐减弱，裂纹路径逐渐恢复到Ⅰ型裂纹的形式；裂纹扩展路径如图11(a)所示。当裂纹刺入软夹杂后，裂尖处在一个被较硬基体包围的软材料内，因此能量释放率远低于裂尖位于夹杂外的情况。从图11(c)可看到，此时的应力强度因子KI出现了突变，直到裂纹刺穿夹杂后，应力强度因子才恢复到原先的变化趋势。

(a)裂纹扩展路径

(b)能量释放率

(c)含有软夹杂平板的应力强度因子

改变夹杂与裂纹的相对位置与弹性模量，比较不同情况下的裂纹扩展路径，对比结果如图12所示：夹杂离裂纹扩展路径越近，对裂纹路径的影响越大；对于硬夹杂，夹杂与母材的弹性模量比EⅠ/E越大，夹杂对裂纹的影响越大；对于软夹杂，夹杂与母材的弹性模量比EⅠ/E越小，夹杂对裂纹的影响越大。

从本节算例的结果可看出，在纯拉伸状态下，裂纹沿着垂直于载荷的方向扩展，当附近存在夹杂时，裂纹会首先向材料刚度小的方向扩展，在越过夹杂之后逐渐恢复到垂直于载荷的方向。

(a)d增大时裂纹扩展路径

(b)EI增大时裂纹扩展路径

3.3.2裂纹经过一对夹杂

考虑文献[14]中裂纹经过一对夹杂的情况，夹杂半径R=5 mm，EⅠ/E=6.43，v=0.33，v1=0.17，2个夹杂的圆心连线与水平面的夹角θ分别为60°和30°，距离S=3R。母版的尺寸、材料以及加载方式与3.3.1节相同，裂纹增量为1 mm。模拟结果如图13所示。对于θ=30°的情况，裂纹在刺入夹杂之前的路径与文献[14]的计算结果基本吻合，裂纹跨过第一个夹杂之后，裂尖后方的区域被加强了，由于位置关系，第二个夹杂对裂纹的抑制作用无法迫使裂纹完全偏离夹杂而只是方向略往上偏，最终刺入夹杂。由于此时无量纲能量释放率远大于裂尖在夹杂外的情况，影响了曲线特征的显示，故没有显示该段的数据曲线。从图13(d)的应力强度因子曲线可看出，裂尖的应力强度因子KI在裂纹刺入夹杂之后出现了突变，远大于裂尖在母材中的情况，直到裂纹刺穿夹杂后才恢复到原先的变化趋势。图14是进入夹杂影响区域后裂尖在几个典型位置的y方向应力云图，反映了一对夹杂相互作用下裂尖附近应力场的分布情况。

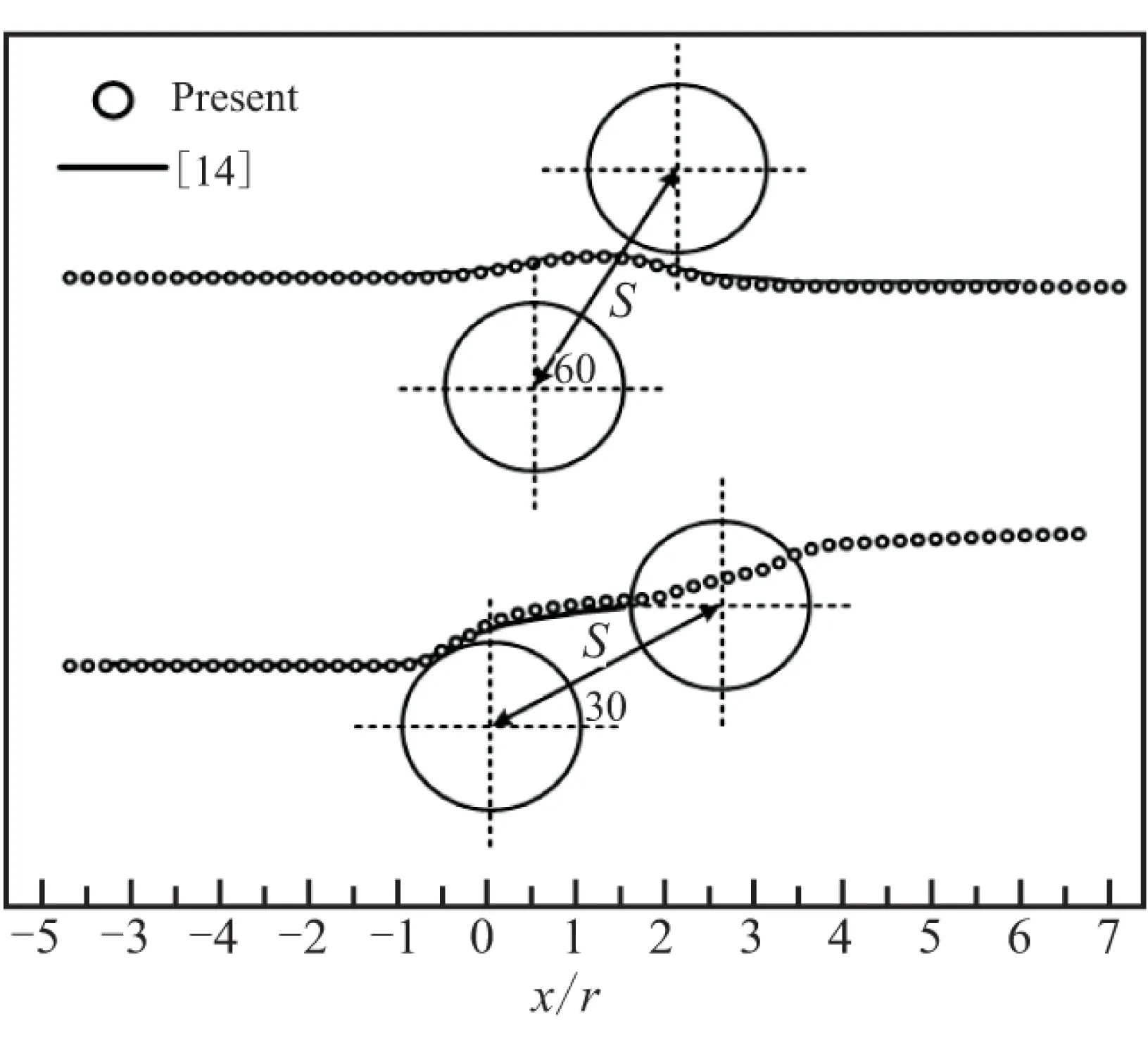
(a)裂纹扩展路径

(b)θ=60°能量释放率

(c)θ=30°能量释放率

(d)θ=30°应力强度因子

(a)Step 20，当θ=60°　　　　(b) Step 30，当θ=60°

(c)Step 25，当θ=30°　　　　(d) Step 35，当θ=30°

3.3.3裂纹经过一组不规则分布的夹杂

在实际情况中，夹杂通常是成群存在的。使用图6所示的模型和加载方式，在板中心的矩形区域设置图15所示的一组12个夹杂，图中H=20 mm，圆形夹杂的半径R=3 mm，椭圆形夹杂的长轴半径a=3.75 mm，短轴半径b=2.5 mm，夹杂与母材的弹性模量比EⅠ/E=10。取初始裂纹长度a0=25 mm，裂纹增量为1 mm，计算裂纹扩展路径。裂纹经过夹杂区域时的扩展路径如图15所示，裂纹方向只有轻微的变化；从图16可看出,裂尖处在夹杂区域时无量纲能量释放率始终小于1，表明两侧的硬夹杂抑制了疲劳裂纹的扩展。

图15　裂纹经过一组12个夹杂

图16　无量纲能量释放率

4　结论

(1)与更新网格方法的对比结果证明,使用扩展有限元方法结合水平集方法模拟疲劳裂纹在含夹杂体中的扩展寿命具有很好的精度，且在使用较稀疏网格的情况下即可获得较高的计算精度。

(2)刚度大于母材的夹杂能降低附近的裂纹扩展速率，并能迫使裂纹向偏离自己的方向扩展；虽然夹杂在较远的位置(大约5～6倍夹杂半径)就会影响裂尖的能量释放率，但裂纹直到非常靠近夹杂时才会改变扩展方向。

(3)当夹杂刚度小于母材，或者多个夹杂综合作用时，裂纹可能刺入夹杂，此时应力强度因子以及能量释放率出现突变，直到裂纹刺穿夹杂，应力强度因子的变化才回复到原先的变化趋势。

[1]Tamate O.The effect of a circular inclusion on the stresses around a line crack in a sheet under tension[J].International Journal of Fracture Mechanics,1968,4(3):257-266.

[2]Atkinson C.The interaction between a crack and an inclusion[J].International Journal of Engineering Science,1972,10(2):127-136.

[3]Erdogan F,Gupta G D,Ratwani M.Interaction between a circular inclusion and an arbitrarily oriented crack[J].Journal of Applied Mechanics,1974,41(4):1007-1013.

[4]Thomson R D,Hancock J W.Local stress and strain fields near a spherical elastic inclusion in a plastically deforming matrix[J].International Journal of Fracture,1984,24(3):209-228.

[5]Zhang J,Katsube N.A hybrid finite element method for heterogeneous materials with randomly dispersed elastic inclusions[J].Finite Elements in Analysis and Design,1995,19(1):45-55.

[6]Wang Y B,Chau K T.A new boundary element method for mixed boundary value problems involving cracks and holes:Interactions between rigid inclusions and cracks[J].International Journal of Fracture,2001,110:387-406.DOI:10.1023/A:1010853804657.

[7]Knight M G,Wrobel L C,Henshall J L,et al.A study of the interaction between a propagating crack and an uncoated/coated elastic inclusion using the BE technique[J].International Journal of Fracture,2002,114(1):47-61.

[8]Kitey R,Phan A V,Tippur H V,et al.Modeling of crack growth through particulate clusters in brittle matrix by symmetric-Galerkin boundary element method[J].International Journal of Fracture,2006,141(1-2):11-25.

[9]Melenk J M,Babuška I.The partition of unity finite element method:basic theory and applications [J].Computer methods in applied mechanics and engineering,1996,139(1):289-314.

[10]Belytschko T,Black T.Elastic crack growth in finite elements with minimal remeshing[J].International Journal for Numerical Methods in Engineering,1999,45(5):601-620.

[11]Dolbow J,Belytschko T.A finite element method for crack growth without remeshing[J].Int.J.Numer.Meth.Engng.,1999,46(1):131-150.

[12]Sukumar N,Chopp D L,Moes N,et al.Modeling holes and inclusions by level sets in the extended finite-element method[J].Computer Methods in Applied Mechanics and engineering,2001,190(46):6183-6200.

[13]Yu H,Wu L,Guo L,et al.Investigation of mixed-mode stress intensity factors for nonhomogeneous materials using an interaction integral method[J].International Journal of Solids and Structures,2009,46(20):3710-3724.

[14]Wang Z,Ma L,Wu L,et al.Numerical simulation of crack growth in brittle matrix of particle reinforced composites using the XFEM technique[J].Acta Mechanica Solida Sinica,2012,25(1):9-21.

[15]Natarajan S,Kerfriden P,Mahapatra D R,et al.Numerical analysis of the inclusion-crack interaction by the extended finite element method[J].International Journal for Computational Methods in Engineering Science and Mechanics,2014,15(1):26-32.

[16]Duflot M.A study of the representation of cracks with level sets[J].International Journal for Numerical Methods in Engineering,2007,70(11):1261-1302.

[17]Sethian J A.A fast marching level set method for monotonically advancing fronts[J].Proceedings of the National Academy of Sciences,1996,93(4):1591-1595.

[18]Hutchinson J W.Mixed mode cracking in layered materials[J].Advances in Applied Mechanics,1991:63-191.

[19]Kim J H,Paulino G H.Consistent formulations of the interaction integral method for fracture of functionally graded materials[J].Journal of Applied Mechanics,2005,72(3):351-364.

(编辑：薛永利)

Fatigue crack behavior in metallic panels with inclusions using XFEM

SHU Yi-xiu，LI Ya-zhi，SHANG Hai-jiang，JIANG Wei

(College of aeronautics，Northwestern Polytechnical University，Xi’an710072，China)

Fatigue crack propagation behaviour is remarkably affected by inclusions in homogenous material because of the stress redistribution.For the purpose of analyzing the influence pattern of inclusions on crack when a crack propagates in non-homogeneous material, an interaction integral method combined with extended finite element method(XFEM)was presented and implemented in ABAQUS using the secondary development environment.Both crack and inclusion are implicitly simulated using enrichment functions and level set method within XFEM framework.The maximum hoop stress criterion was used for crack path prediction.The situation of a crack which propagates through an area containing symmetric or asymmetric inclusions was simulated to analyze the influence of inclusions and their material properties on crack propagation rate and crack propagation path.The situation of a crack penetrating into an inclusion in certain cases was simulated and analyzed.Some of the simulations results agree well with the available results of XFEM,and are validated by the FEM remeshing approach.

fatigue crack propagation；extended finite element method；interaction integral；stress intensity factor；material interface

2015-05-13；

2015-06-24。

束一秀(1988—)，男，博士，研究方向为结构多部位损伤及疲劳断裂。E-mail：shuyixiu@mail.nwpu.edu.cn

V250

A

1006-2793(2016)04-0547-08

10.7673/j.issn.1006-2793.2016.04.018