基于区间值相似度的加权模糊推理
孙晓玲
(合肥师范学院数学与统计学院,安徽合肥 230601)
基于区间值相似度的加权模糊推理
孙晓玲
(合肥师范学院数学与统计学院,安徽合肥 230601)
在相似度的方法用于区间值模糊推理的过程中,为合理地计算区间值加权模糊产生式规则的输入事实与规则前件之间的相似度,给出区间值相似度的计算公式.在此基础上提出基于区间值相似度的加权模糊推理算法.为体现规则前件断言对于规则结果的重要性程度,在区间值模糊产生式规则中加入了权值参数.为了采用该算法,给出区间值排序的方法.最后用实例说明所给出的推理算法更符合实际需要,可操作性强,便于应用.
区间值模糊产生式规则;区间值相似度;加权模糊推理;区间值模糊推理;区间值排序
0 引言
随着社会经济的发展,人们碰到的知识和信息的不确定性和不完备性的持续增加,单纯用数值来处理这些信息是很不合理的,而区间值可以用来表示这些信息,因此近年来关于区间值有关问题的研究正受到很多研究者的关注.区间值模糊推理是区间值模糊集的推理,在实际应用中,一个对象的隶属度往往不容易确定,而区间值隶属度相对而言较易确定,并且区间值模糊推理方法可以减少推理过程中模糊信息的丢失.曾文艺等提出了模糊产生式规则的推理方法[1],给出了加权模糊匹配函数和区间值排序算法.李凡、符海东等给出了区间数相似度的计算公式与区间数排序的可能度公式之间的关系,根据区间数与目标区间数相似程度的不同,提出新的对区间数进行排序的方法[2-3].Zhang等人给出基于S-OWA算子的加权区间值模糊推理算法[4],该算法采用S-OWA算子为区间值模糊产生式规则前件各个命题分配权值,算法较灵活简单.区间数相似度的计算公式与区间数排序的可能度公式之间的关系,根据区间数与目标区间数相似程度的不同,提出新的对区间数进行排序的方法[5-7].
由于在模糊推理中,规则前件对推理的支持程度不同,对规则所做的贡献不同,因此前件中各个命题的重要程度也不一样,但已有文献中将区间值模糊产生式规则的前件与事实命题匹配时较少考虑给规则的前件各个命题分配权值,这样就不能够体现前件中的不同命题对于规则结果的重要性程度,另外,已有文献对于基于多层模糊推理的区间值模糊推理方法也没有涉及.为了更好的模拟人类的决策思维和推理过程,本文提出基于区间值相似度的加权模糊推理算法,首先给出区间值加权模糊产生式规则的定义,然后给出区间值模糊产生式规则的前件断言与结果之间的相似度的计算方法,最后基于此方法给出区间值加权模糊推理结果的计算方法.
1 区间值的概念与区间值排序
回顾区间值的相关概念,给出区间值相似度的计算公式以及区间值排序的方法.
1.1区间值的定义
隶属函数经常被用来描述模糊集合,但由于经常存在模糊集隶属函数对事物的本质规律描述不清楚,或者由于决定隶属函数的因素过多,导致其形式过于复杂,计算出的隶属度与实际值相差很远.但在很多情况下,区间值隶属函数较容易确定,且表达形式简单,更符合实际需要,因此被大量的采用.近年来,有较多关于区间值模糊推理的研究,主要有D-S证据,可能性理论,粗糙集,Vague集等.下面是关于区间值的一些基本概念.
定义1 记a=[a1,a2]={x|0≤a1≤x≤a2≤1},则称a为[0,1]上得一个区间值.特别地,若a1=a2,则a退化为一个实数.[0,1]上全体区间值构成的集合记作I,其中I={[a1,a2],a1≤a2,为区间值a的中心.
1.2区间值相似度
将2个区间值按照某特性进行比较时,通常可通过区间值的相似度或距离来体现比较的结果.区间值相似度是区间值模糊推理的基础,表示2个区间值的接近程度.本节将给出区间值相似度的定义、计算公式以及相关定理.
定义2 设有区间值a=[a1,a2],b=[b1,b2],则称a与b之间的匹配程度为它们的相似度.
定义3 设有区间值a=[a1,a2],b=[b1,b2],且设la=a2-a1,lb=b2-b1,则可用如下公式对区间值a和b的相似度进行计算
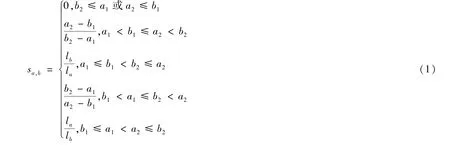
从几何意义上看,sa,b可表示为,其中,|a∩b|,|a∪b|分别为a与b相交部分和a与b相并部分的长度,“∩”和“∪”分别表示“交”和“并”运算.
根据上面定义可得区间值相似度有如下性质:
定理1 sa,b=1当且仅当a=b,即a1=b1,a2=b2,此时称a与b完全相似.
定理2 对任意的3个区间值a,b,c,有如下结论成立:
1)(自反性):s(a,a)=1;
2)0≤s(a,b)≤1,s(a,b)=1⇔a=b;
3)(对称性):s(a,b)=s(b,a);
4)(传递性):s(a,b)=1,s(b,c)=1,则s(a,c)=1,即:如果a和b完全相似,b和c完全相似,则a和c完全相似[5-6].
1.3区间值排序
区间值的序关系是区间值理论的基础,在模糊决策中,常利用模糊量特别是模糊数对备择对象建模,因此备择对象的选择和排序可最终归结为模糊量的选择或排序.由于模糊量本无自然序,所以需要寻找合适的方法确定备择对象的序关系,区间数[8-9]是模糊数的一种,讨论其排序就很有必要.
一般可以根据均值和半径来判断2区间值的大小,均值越大且半径越小的区间值越大,若均值相等,则半径越小的区间数越大.还可以采用均值与半径的商作为区间值排序的依据,e越大,则相应的区间值越大.
2 区间值加权模糊推理
2.1区间值模糊量词与区间值模糊谓词的概念
模糊推理中,常用模糊语言值来表示模糊命题的确定性程度或相应事件发生的可能性程度.所谓模糊语言值是指表示大小、长短、高矮、轻重、快慢、多少等程度的一些词汇.之所以提出用模糊语言值来表示程度的不同,主要是由于这样做更加符合人们表述问题的习惯.用这种方法表示的模糊量词称为区间值模糊量词.对于模糊谓词,将其隶属函数也用区间值表示,称之为区间值模糊谓词.常见模糊量词的区间值[3]如表1所示.
2.2区间值加权模糊产生式规则
在区间值模糊集理论的基础上,我们给出区间值模糊产生式规则的一般形式:
规则R:if(p1,t1,w1)and(p2,t2,w2)and…and,(pn,tn,wn)then Q(CF x)
其中规则前件中的p1,p2,…,pn分别表示断言,每个断言可以包括模糊量词和模糊谓词,或兼而有之.t1,t2,…,tn分别表示断言pi(1≤i≤n)的确定性程度.由于在模糊推理中,规则前件对推理的支持程度不同,对规则所做的贡献不同,因此前件中各个命题的重要程度也不一样,wi是用来表示断言pi对于规则结果Qi的重要性程度的权值.根据专家关于每个断言对产生式规则后件影响程度的经验值或统计值,给规则R赋予权值w={w1,w2,…,wn},wi=1表示完全有影响,wi=0.5表示影响程度为中等,wij= 0表示影响程度是无,常见断言影响程度的权重定义[1]如表2所示,若规则前件仅有一个断言,则不需要给该断言赋予权值.Qi表示规则R的后件,x为确定性因子CF的值,表示规则R的确定性程度.

表1 常见模糊量词的区间值

表2 常见断言影响程度权重
2.3区间值加权模糊推理算法
在知识基中应用区间值加权模糊推理可以遵循以下步骤计算推理的结果及其确定性程度的区间值:
由图5可知,掺加粉煤灰对混凝土在28 d时的水、气体渗透系数的影响大体规律是一致的。掺量在30 %以内,随着粉煤灰的掺量增加,混凝土水和气体渗透系数均随粉煤灰掺量的增加有较明显的降低,表明粉煤灰能有效地降低混凝土的水与气体渗透性。而粉煤灰掺量超过了30 %后,则混凝土的水与气体渗透性有所增加。因此,大掺量粉煤灰不利于降低混凝土的水和气体渗透性[4,9]。但总体上,掺加粉煤灰之后,混凝土的水和气体渗透性均低于对比组1的,其中,降低混凝土气体渗透性的最佳掺量是30 %,而降低混凝土水渗透性的最佳掺量是40 %。
步骤1:由领域专家给出一组带有权值,阈值参数的区间值加权模糊产生式规则以及匹配事实;
步骤2:根据式(1)计算匹配事实pi′(1≤i≤n)分别与区间值加权模糊产生式规则Ri(1≤i≤n)的n个前件断言pj(1≤j≤n)之间的相似度sij(pi′,pj),再根据公式

计算这些相似度的整体相似度,并与阈值所给λ作比较,若SWi≥λ,则规则激发,若SWi<λ,则规则不激发.这里参数λ是阈值,用于指出相应知识在什么情况下可被应用,若可以,则激发规则,推出结果,并计算出结果的确定性因子.
步骤3:在多个规则的知识库中,若根据步骤2判断出能够激发的规则有多条,可利用公式

计算出各条规则结果的确定性程度的区间值,最后利用区间值排序算法,得到最优区间,从而做出决策.
3 算法分析
将2个区间值模糊集按照某特性进行比较时,通常可通过区间值模糊集的相似度或距离来体现比较的结果,区间值相似度是区间值模糊推理的基础.为采用区间值加权模糊产生式规则进行推理,文献[2-3]给出了表示区间值加权模糊产生式规则的前件与匹配事实相似程度的模糊匹配函数,通过将匹配函数值与阈值作比较确定可激发的规则,最后计算推理结果.这里匹配函数的涵义并不明确,不符合相似度的性质.
本文所给的区间值加权模糊推理算法是在式(1)基础上给出的,该算法由于考虑了区间值模糊推理过程中区间值模糊产生式规则前件对于推理结果的重要性程度,因此当区间值模糊产生式规则有多个前件时,可根据式(2)计算考虑权值条件下多个前件与匹配事实的整体相似度,由整体相似度与阈值比较的结果确定可激发的规则从而计算可激发规则确定性程度的区间值并最终做出决策.该推理算法更加接近实际推理并且推理过程更加高效.
4 算例
汽车发动机所有可能的故障表现为:
1)发动机不能启动;2)发动机加速不良;3)发动机怠速不良;4)发动机怠速过高;5)发动机转速不稳;6)发动机回火.
这些故障表现的全体构成集合为:

导致这些故障的原因分别为:
1)蓄电池电压过低;2)点火时间过晚;3)进气系统漏气;4)节气门被卡不能关闭;5)空气滤清器滤芯堵塞;6)混合气过稀.
这些故障原因构成的集合为:

发动机故障表现所具有的确定性程度分别为:

领域专家根据经验给出各前件断言的权重为:

区间值加权模糊产生式规则的阈值为:λ=0.5.
知识库中含有以下6条规则R1,R2,…,R6分别为:

用户输入的与规则前件断言匹配的事实分别为:

根据式(1)可以分别计算出匹配事实p1′与第1条规则R1的各个前件断言匹配后得到的相似度分别为:

这些相似度的整体相似度为


由上面结果可知规则R3,R5,R6将被激发执行,得到规则后件结果的确定性程度为:

用1.3中介绍的区间值排序的方法对这3个区间值进行排序可得:

由计算结果可知最大区间值为Q6=[0.536,0,67],这表示故障最有可能是由原因q2导致,其确定性程度的区间值为[0.536,0,67].
5 结束语
为研究区间值加权模糊推理,给出了计算区间值之间的相似度计算公式,以及区间值排序的方法,提出的区间值加权模糊推理算法可以计算出区间值加权模糊推理的结果以及推理结果的确定性程度的区间值.由于在区间值模糊产生式规则中加入了权值参数,推理结果能够体现规则中的不同前件断言对规则结果的重要性程度.另外区间值加权模糊推理方法中还考虑了多规律知识系统中做决策时的最优选择问题,给出的方法可以使推理更接近实际情况,便于应用.
[1] 曾文艺,于福生,李洪兴.区间值模糊推理[J].模糊系统与数学,2007,21(1):68-74.
[2] 李凡,徐章艳.一个有效的区间值模糊推理方法[J].应用科学学报,2000,18(4):327-330.
[3] 符海东,雷大江.区间值加权模糊推理方法[J].计算机工程与应用,2005,41(6):57-59.
[4] Zhang Q S,Li B.Multidimensional interval-valued fuzzy reasoning approach based on weighted similarity measure[J]. Fuzzy Information and Engineering,2011,3(1):45-57.
[5] Chen S M,Lee L W,Shen VRL.Weighted fuzzy interpolative reasoning systems based on interval type-2 fuzzy sets[J].Information Sciences,2013,248(6):15-30.
[6] 许瑞丽,徐泽水.区间数相似度研究[J].数学的实践与认识,2007,37(24):1-8.
[7] 兰继斌,胡明明,叶新苗.基于相似度的区间数排序[J].计算机工程与设计,2011,32(4):1419-1421.
[8] 李大东.区间数的排序和它的一些应用[D].成都:西南交通大学,2004.
[9] 董九英.高校教师教学质量评估的区间数方法[J].计算机工程与应用,2010,46(17):246-248.
Weighted Fuzzy Reasoning Based on Interval Value Similarity Measure
SUN Xiao-ling
(School of Mathematics and Statistics,Hefei Normal University,Hefei Anhui 230601,China)
In the fuzzy inference method,similarity-based fuzzy reasoning method is a kind of simple and important method.This method is used for the interval valued fuzzy inference process.For the purpose of calculating the similarity measure between the input facts and antecedent portion of the interval value weighted fuzzy production rules,interval value similarity measure calculation formula is proposed.On the basis of the interval valued similarity measure,a weighted fuzzy reasoning algorithm is proposed.The weight parameter is added to the interval valued fuzzy production rules to reflect the importance degree of the antecedent assertion for the reasoning result.In order to use the algorithm,a kind of interval value ranking method is proposed.Finally,an example is illustrate to show the proposed reasoning algorithm is more consistent with the actual needs,strong operability and convenient for application.
interval valued fuzzy production rules;interval value similarity measure;weighted fuzzy reasoning;interval valued fuzzy reasoning;interval value ranking
TP273+4
A
1671-6876(2016)03-0193-06
[责任编辑:李春红]
2016-04-15
安徽省高校自然科学研究重点资助项目(KJ2016A580)
孙晓玲(1977-),女,安徽合肥人,副教授,硕士,研究方向为不确定性模糊推理等.E-mail:sxl-hftc@126.com

