双重广义线性模型在车损险费率厘定中的应用
赵明清,陈玉澎,张晓晓
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
【统计应用研究】
双重广义线性模型在车损险费率厘定中的应用
赵明清,陈玉澎,张晓晓
(山东科技大学 数学与系统科学学院,山东 青岛 266590)
双重广义线模型是对广义线性模型的扩展,其对反应变量的均值与散度参数同时建立模型,提高了模型运用的灵活性与适应性。将双重广义线性模型应用到车损险费率厘定中,既考虑了费率期望值与费率因子之间的关系,又考虑了变量的分散程度与费率因子之间的关系,并以欧洲一家保险公司的汽车保险损失数据为样本进行实证研究,把无索赔优待等级、地区、车型与年均行驶里程数作为费率因子,建立了费率厘定模型。结果表明,所得到费率结构合理,符合实际。
双重广义线性模型;散度参数;车损险;费率厘定
一、引 言
中国于2003年启动车辆保险条款费率管理制度改革,2015年正式发布《深化商业车险条款费率管理制度改革试点工作方案》,明确提出了商业车险改革的时间表与路线图。经过十几年的探索,车险费率市场化工作取得了长足进步,但要真正全面实现仍需很长一段时间。推进费率市场化需要更加精准的定价与公平合理的费率结构,精算技术的发展与运用是其实现的重要保证,只有建立科学合理的精算假设,运用灵活适当的精算模型才能保证保险公司针对不同的客户提供差别化的定价、个性化的费率。
广义线性模型(GLM)作为对经典线性模型的推广,由Neledr于1972年提出。McCullagh等人首次将GLM应用到精算领域中[1]317-358。自此,GLM在非寿险费率厘定中得到了广泛的应用,并且已成为车险费率厘定的标准方法。然而,伴随着精算理论的发展以及实务上对费率厘定精度要求的进一步提高,GLM在应用中也暴露出了一些缺陷,为此学者们对其进行了多种扩展。Pregibon等人提出了关于反应变量均值与散度参数同时建立模型的双重广义线性模型(DGLM),将传统的广义线性模型进行进一步地推广[2];Smyth引进DGLM的极大似然估计,考虑了总体服从正态、逆高斯分布时的情形[3];Smyth使用限制性极大似然估计对DGLM的参数进行了估计,并以实例进行了验证[4];王大荣考虑了DGLM中的变量选择问题,提出了新的模型选择准则[5];吴刘仓等采用最近距离插补法和反距离插补法对缺失数据情况下的DGLM参数估计进行了研究[6];Smyth把DGLM应用到非寿险定价中,对车损险费率进行预测,但在实证研究中剔除了地区因素,得到的费率结构并没有体现地域差异[7]。目前,国内将DGLM与车损险费率厘定相结合的研究文献尚没有见到。
本文应用DGLM对索赔次数数据缺失情形下的车损险费率厘定进行研究,将地区因素纳入到费率因子中,并对相关参数进行了优化选择,使得到的费率结构更加合理,符合实际。
二、车损险费率厘定的DGLM
在通常的GLM中,只建立反应变量Y的期望值μ与解释变量之间的回归关系,而假设散度参数φ是固定的常数,这种假设虽然可以简化模型,但在某些情况下与实际情况并不相符。因为除了正态分布、二项分布、伽玛分布与泊松分布等标准分布外,φ很少是已知的[8]。DGLM弥补了这种局限性,其形式如下:
(1)
其中,yi为反应变量Y的第i个观测值,yi间相互独立且服从某一类指数族分布;n为样本容量;μi为yi的均值,g(μi)=Xiβ为均值主模型的连接函数;ωi为yi对应的先验权重;V(μi)是方差函数;gd(φi)=Uiγ为散度子模型的连接函数,其反应变量为均值主模型的单位偏差,衡量了Y与μ之间的距离;Xi=(Xi1,Xi2,…,Xip)和Ui=(Ui1,Ui2,…,Uiq)分别为均值主模型与散度子模型解释变量的第i组观测值,主模型与子模型的解释变量可以不同;β=(β1,β2,…,βp)T为均值主模型的p×1维待估参数向量,γ=(γ1,γ2,…,γq)T是散度子模型的q×1维待估参数向量。
DGLM允许对反应变量期望值和散度参数同时建立广义线性模型,而且方差与期望值的关系式也发生了改变,φi已不再是一个固定的常数。采用DGLM建立车损险费率模型,既要考虑费率期望值与费率因子之间的关系,又要考虑变量的分散程度与费率因子之间的关系[9]。
假设共有n个费率单元(即样本容量为n),Ni为第i个费率单元的索赔次数随机变量,mi为其风险单位数随机变量,Ci为其索赔额随机变量,则Pi=Ci/mi表示每一风险单位的平均索赔额随机变量。设Ni~Poi(λimi),λi为该费率单元内每一风险单位的期望索赔次数,单次索赔的发生是独立的,单次索赔额服从期望为τi、形状参数为α的伽玛分布。可以证明[7]:
μi=E(Pi)=λiτi
(2)
(3)
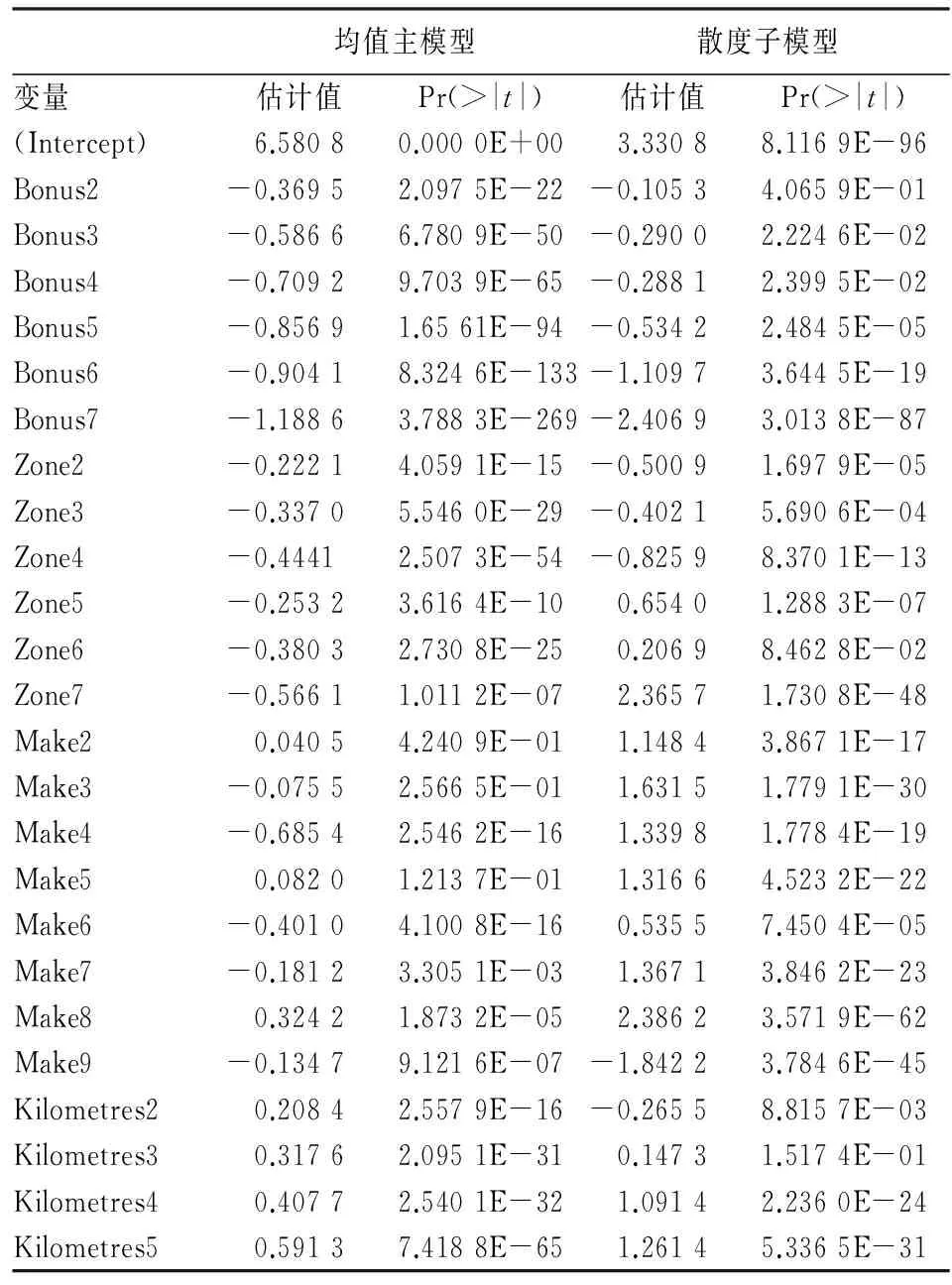
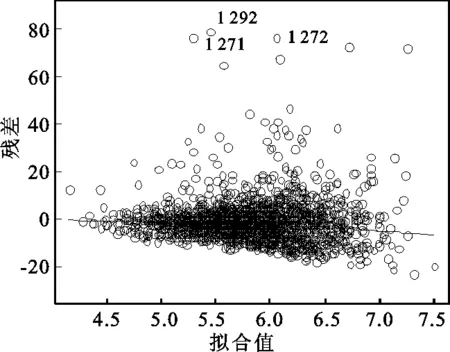
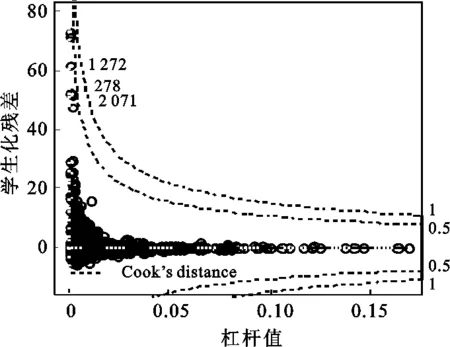
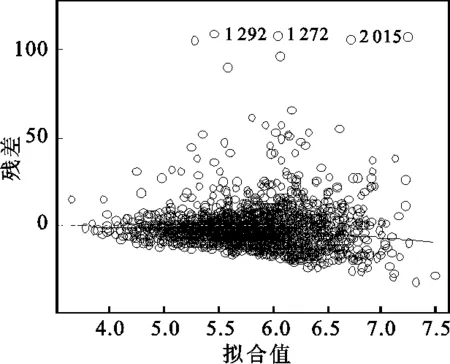
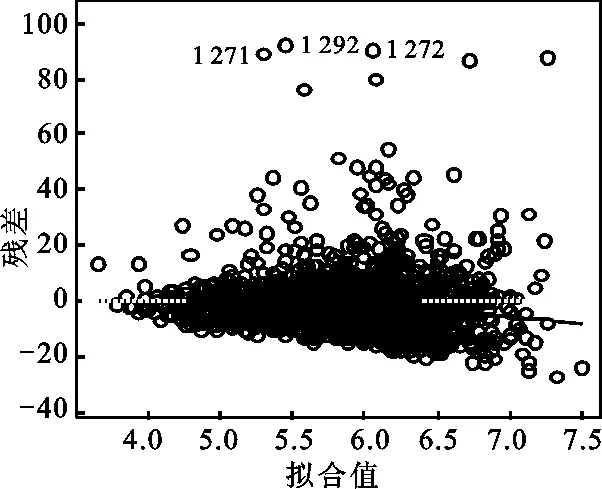
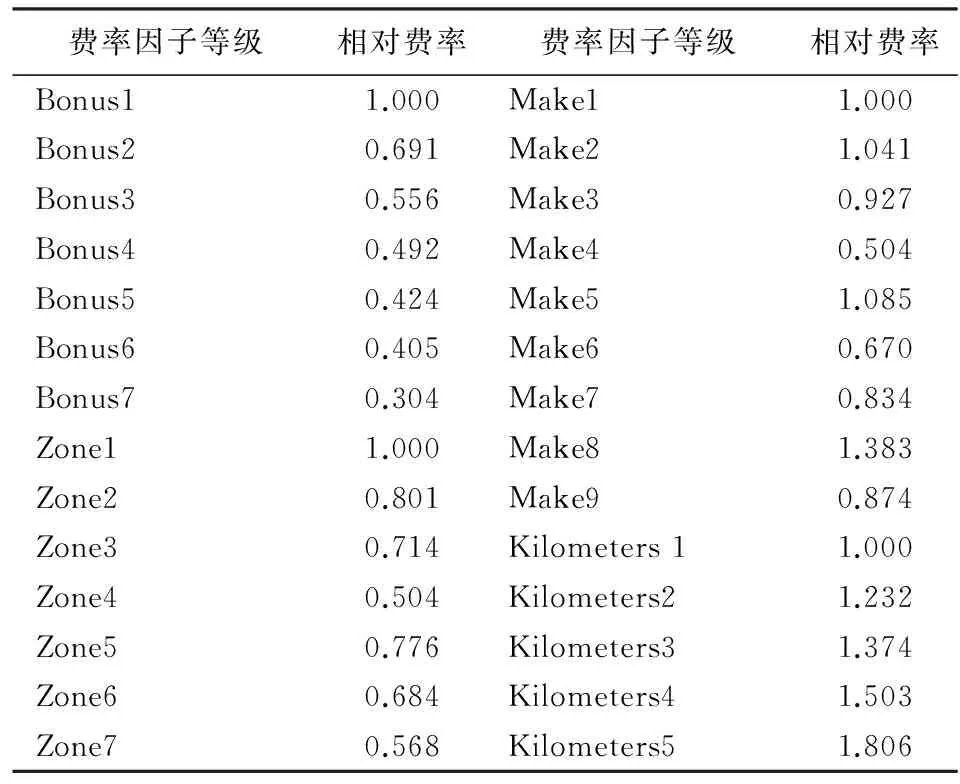
μi即为该费率单元内每一风险单位的费率期望值(以下简称费率期望值)。方差函数中p=(α+2)/(α+1),因为α>0,所以1 (4) 其中,φ=1,ωi=mi/φi,Xi为均值主模型的费率因子设计矩阵中第i个费率单元对应的行向量。 (5) Ui为散度子模型的费率因子设计矩阵中第i个费率单元对应的行向量。主模型与子模型的费率因子可以根据实际情况分别选择。 对GLM进行参数估计的经典方法是建立参数的似然方程,通过迭代加权最小二乘法对方程求解。该方法对于DGLM同样适用,在两个模型间交替使用极大似然估计法可以得到β和γ的估计值。当固定γ与p的取值时,可以通过对均值主模型使用极大似然估计法对β进行估计;当固定β与p的取值时,同样可以使用极大似然估计法对子模型的γ进行估计。具体过程可参见Smyth和梅长林文献[7] [11]56-67。 在得到模型的参数估计结果后,需要对参数的显著性、模型的拟合优度及稳健性进行检验。 综上所述,应用DGLM厘定车损险费率的主要步骤有:搜集数据,对数据进行分类、整理、描述;确定均值主模型与散度子模型的费率因子;确定模型的相关参数与连接函数,建立DGLM;利用极大似然估计法对参数进行估计;对参数估计进行显著性和稳健性检验,对模型进行拟合优度检验;根据通过检验的DGLM计算费率。 本文使用R软件进行数据分析,数据来源于瑞典一家保险公司的第三方汽车保险损失数据,可通过访问www.statsci.org/data/general/motorins.html获得。 该组数据包含7个变量:年均行驶里程数(Kilometers,5个等级)、地区(Zone,7个等级)、无索赔优待等级(Bonus,7个等级)、车型(Make,9个等级)、风险单位数(Insured)、索赔次数(Claims)、索赔额(Payment),变量的分级依据及实际含义详见以上网址。在建模过程中未使用索赔次数数据,只利用其他6个变量的信息。 每一个费率因子选定一个等级作为基础水平,基础水平对应的模型参数取零,对其他等级估计相应的参数(包含截距项在内,均值主模型与散度子模型均有25个待估参数)。基础水平的选择不影响最终的费率估计结果,选择费率单元(1,1,1,1)为基础水平单元。 对模型(4)、(5)交替使用极大似然估计得到的参数估计结果如表1所示。 从表1的结果可以看出,相同的费率因子对均值与散度参数的影响程度、方向并不完全相同,但两个模型的参数在绝大多数因子等级上显示了较强的显著性,这说明对散度参数建立模型是有必要的。 表1 参数估计结果表 图1为残差与拟合值图,从图1中可以直观地看出几乎所有的拟合值的残差分布在(-40,40)这个区间内,只有很少的点超出此区间,说明模型拟合效果比较理想。 图1 残差与拟合值图 图2 学生化残差与杠杆值图 图2为学生化残差与杠杆值图,所有观测值对应的残差与杠杆值点都位于图上部两条虚线的下方,这说明当对每一风险单位的平均索赔额建立DGLM时只存在少数结果残差较大,模型是合适的(例如第278、第1 272与第2 071风险单元,平均索赔额都超过了6 000,可以视为特殊情形)。 在Tweedie类分布中,概率分布的具体形式由方差函数V(μ)=μp中p的取值决定。当改变p的取值时,模型估计得到的参数也会发生变化,进而会影响模型的拟合效果,所以本文采用改变p值,观察残差变化的方式来检验参数的稳健性。 令p在(1.13,1.23)的范围内变动,发现参数估计结果的符号及显著性没有发生明显的变化,误差均保持在(-0.01,0.01)内。以p取1.13和1.23时的残差为例(见图3、图4),与图1相比,当p=1.13时,残差值虽有一定程度的增大,但在可接受的范围内;当p=1.23时,残差值同样有所增加,但绝大部分残差值依然分布在(-40,40)的范围内。因此,DGLM的参数估计结果具有较好的稳健性。 图3 p=1.13残差与拟合值图 图4 p=1.23残差与拟合值图 模型通过检验,可以利用其参数结果计算费率。由于采用对数函数为连接函数,故费率期望值的计算公式为: (6) 表2 相对费率表 综合参数输出结果与估计费率可发现: 第一,随着无索赔优待等级的提高,相对费率在降低,这符合实际中的情况,对风险低的驾驶员应给予更大的优惠,降低其续年年费。无索赔优待系统各个等级的均值主模型参数在0.01水平下均是显著的,但个别散度子模型参数显著性较差。 第二,不同行驶区域对费率的影响程度并不相同,地区7的索赔次数是最少的,可能导致其显著性不强,输出的结果也证实了地区7的均值主模型参数显著性确实相对较低。 第三,在8个车型类别中,车型8的相对费率最高,达到了1.383;车型4的相对费率最低,为0.504;均值主模型中车型2、3、5的参数显著性最差,可以考虑将三者合并以提高影响力。 第四,均值主模型中年均行驶里程数各个等级的参数在0.01水平下都显著。年均行驶里程数越高,发生风险的可能性也在相应增加,这在相对费率的结果上得到了很好的体现,年均行驶里程在水平5(25 000公里以上)的相对费率增至1.806。 DGLM作为传统广义线性模型的推广,放松了散度参数为常值的假设,允许对均值和散度参数同时建立广义线性模型,提升模型运用的灵活性,改善模型的拟合效果。本文将DGLM应用到车损险费率厘定中,在无索赔次数数据情况下对纯保费直接建模,得到的费率结构符合实际,较为公平、合理。 纯保费的估计只是非寿险定价中的一个环节[12],除此之外,更多的要考虑公司的战略定位、市场环境、目标人群与外部监管环境等宏观因素,并对附加保费也要做出合理的估计。本文仅对DGLM模型在车损险费率厘定中的一个案例进行了分析,虽然得到了较为满意的结果,但是可否在非寿险精算领域中推广其应用还有待于进一步研究。 [1]McCullagh P, Nelder J A, et al. Generalized Linear Models (Second Edition)[M].London: Chapman and Hall,1989. [2]Pregibon D. Review:McCullagh P, J A Nelder, Generalized Linear Models[J]. Annals of Statistics, 1984, 12(4). [3]Smyth G K. Generalized Linear Models with Varying Dispersion[J]. Journal of the Royal Statistical Society, 1989(1). [4]Smyth G K, Verbyla A P. Adjusted Kikelihood Methods for Modeling Dispersion in Generalized Linear Models[J]. Environmetrics, 1999, 10(6). [5]王大荣. 分散度量模型中的变量选择[D]. 北京:北京工业大学, 2009. [6]吴刘仓, 邱贻涛, 詹金龙. 缺失数据下双重广义线性模型的参数估计[J]. 应用数学, 2014, 27(4). [7]Smyth G K, Jørgensen B. Fitting Tweedie's Compound Poisson Model to Insurance Claims Data: Dispersion Modelling[J]. Astin Bulletin, 2002, 32(1). [8]徐登可. 异方差模型的统计推断[D]. 北京:北京工业大学博士论文, 2013. [9]曾娟. 机动车辆保险分类费率厘定原理与方法研究[D]. 武汉:武汉理工大学博士论文, 2008. [10]卢志义, 刘乐平. 广义线性模型在非寿险精算中的应用及其研究进展[J]. 统计与信息论坛, 2007, 22(4). [11]梅长林, 王宁. 近代回归分析方法[M]. 北京:科学出版社, 2012. [12]陈正,汪飞飞.贝叶斯方法在调整保险费率中的应用[J].西安财经学院学报,2012(5). (责任编辑:张爱婷) Double Generalized Liner Models and Its Application in Ratemaking of Auto Damage Insurance ZHAO Ming-qing, CHEN Yu-peng,ZHANG Xiao-xiao (College of Mathematics and System Science, Shandong University of Science and Technology, Qingdao 266590, China) Double generalized linear model is an extension of the generalized linear model. It is used to establish the generalized linear model of mean and dispersion parameter, which improves the flexibility and adaptability of the model. The double generalized linear model is applied to the vehicle damage insurance ratemaking, not only the relationship between rate expectations and the rate factor is considered, but also the relationship between the degree of dispersion and the rate factors. The loss data of the insurance company in Europe is used as the sample to carry out the empirical research. The rate determining model is established with bonus, zone, make and annual mileage as the rate factors. The results show that the insurance rate structure is reasonable and practical. double generalized linear model; dispersion parameter; vehicle damage insurance; ratemaking 2016-01-15;修复日期::2016-04-28 国家自然科学基金青年项目《基于结构化大数据深度挖掘的非寿险保险公司经营风险模型研究》(61502280);山东省研究生教育创新计划资助项目《基于大数据的金融硕士专业学位研究生培养模式与实践措施研究》(SDYY14086);山东科技大学研究生科技创新基金项目《基于分层广义线性模型的非寿险定价研究》(YC150337) 赵明清,男,山东临朐人,教授,工学博士,研究方向:保险精算; F840.65 A 1007-3116(2016)10-0042-05 陈玉澎,男,山东海阳人,硕士生,研究方向:精算学与风险管理; 张晓晓,女,山东德州人,硕士生,研究方向:精算学与风险管理。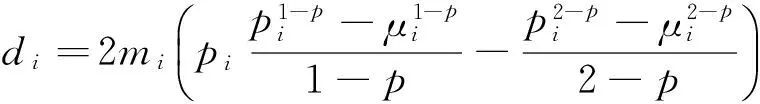
三、实证分析
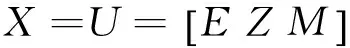
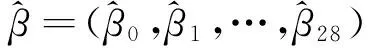
四、结 论

