基于信息可替代性的评价指标筛选研究
陈洪海
(南京财经大学 金融学院,江苏 南京 210023)
【统计理论与方法】
基于信息可替代性的评价指标筛选研究
陈洪海
(南京财经大学 金融学院,江苏 南京 210023)
提出一种指标筛选方法,旨在筛选出对评价结果影响显著、反映信息重叠程度低的评价指标。以相对离散系数作为指标的信息含量,依据提出的累计信息贡献率标准删除信息含量明显偏小的指标进行指标的初筛,克服现有研究仅利用相对离散系数进行指标筛选的不足。借鉴聚类分析的思想,取初筛后保留下来的一个指标与其余各指标构成Person相关系数平方的均值,反映该指标的信息可被其余全部指标替代的程度。通过信息可替代性标准剔除信息可替代性较大的指标,保证最终被保留的指标间反映的信息重叠程度低,克服现有研究仅通过两个指标间的相关性筛选指标难以有效降低评价指标集信息重叠的不足。此外,针对剔除信息重叠的指标与剔除对评价结果影响不显著的指标何者优先为宜的问题,提出了显著再相关的指标筛选标准。最后,通过一个实例说明指标筛选方法的可行性。
评价指标;指标筛选;信息可替代性;信息重叠
一、引 言
综合评价是为反映评价对象的全貌,按照某种方法将体现评价目的与内容的诸多指标的信息汇集成一个综合性指标,从整体上判别评价对象状态水平的评价方法。目前,综合评价方法在科技与经济评价等经济及社会发展的诸多领域中得到了极其广泛的应用,对有关部门科学决策发挥了非常重要的作用。综合评价的前提是评价指标体系的构建。而指标体系构建的合理性直接影响评价结果的合理性。综合评价的实践中常常会遇到体现评价目的与内容的指标数量很大,导致评价信息过度重叠。而相互重叠的那部分指标信息在综合评价时会被过度夸大,从而导致评价结果的合理性无法得到保证。同时,如果评价指标数量过于庞大也会导致评价系统迟钝及“数字黑洞”的出现。因此,必须对原始指标体系加以精简,通过指标筛选剔除部分反映信息重叠的指标。
目前,评价指标定量筛选方法主要包括两类。一是利用指标间的某种相关性,剔除反映信息重叠的部分指标;二是利用指标本身取值上的变异性,剔除区分度不显著、对评价结果影响弱的指标。通过相关性分析剔除反映信息重复的部分指标的方法主要包括如下三类。
一是利用Person相关系数或偏相关系数剔除反映信息重叠的指标。Person相关系数是采用皮尔逊积差相关法对两个指标间的相关性进行分析的一种线性相关系数。偏相关系数是在考虑了其它相关指标影响的条件下表示两个指标间相关程度的一种相关系数。这两种相关系数均能刻画两个指标间的线性相关程度。比如Mitra、韩伯棠、迟国泰等通过相关系数进行相关性分析,删除任意两个相关程度比较高的指标中对评价结果而言相对不重要的指标[1-3]。
二是利用互信息剔除反映信息重叠的指标。互信息是信息论中主要利用信息熵量化的一种无参、非线性的衡量指标间相关程度的工具[4]。互信息表示两个指标间共有信息的含量,可以反映两个指标间的相互关联强度的大小。为了实现指标的筛选功能,通常会采取剔除互信息较大的指标中相对不重要的指标或与其它方法相结合的方式来实现[5-8]。互信息的不足在于其对临界特征的概率影响较为敏感[9],而且仅用互信息进行指标筛选的效果并不理想[10]。
三是利用聚类分析间接剔除指标间的重叠信息。聚类分析包括Q型聚类分析和R型聚类分析。两种聚类分析的适用对象分别为样品和指标。R型聚类分析可将指标集分成若干不同的子类,不同之类间指标相关程度低,而同一子类内的指标间相关程度高。现有研究通常通过R型聚类分析将原始指标集分成若干个子类,再在每个子类内仅选择最重要的一个指标,从而实现评价指标间信息重叠程度的降低[11-13]。但是目前聚类分析子类数量的确定方法依然存在争议,而且容易陷入局部极优[14]。
上述利用相关性分析筛选指标方法需要确定相关程度高的指标中哪一个对评价结果影响最大。目前,对评价结果影响程度的确定主要通过两种方式。一是结合指标的内涵、综合评价的目的、目标及专家的经验确定指标对评价结果影响程度。二是通过模糊隶属度、灰色关联度、主成分的负载系数、变异系数等定量分析的方法确定。
指标集内部指标间是相互影响、相互作用的。因此,利用指标间的相关性筛选指标应该依据每个指标与其余全部指标构成的指标集间的相关性来决定指标的取舍,而不是仅利用两个指标间的(偏)相关系数或互信息来决定指标的取舍。因为Person相关系数、偏相关系数或互信息测度的仅是两个指标间的相关性,并不能度量一个指标与其余全部指标间的相关性。因此,现有的利用指标间的相关性筛选指标的方法并不能有效减低指标集间的信息重叠。
针对现有研究存在的上述问题,本文提出了基于指标信息可替代性的指标筛选方法。在综合评价中指标筛选的两大核心任务分别是剔除对综合评价结果影响较弱的指标及降低评价指标间的信息重叠程度。本文借鉴聚类分析测度两指标集间相似性的类平均法思想,将指标Xi与其余每个指标间的相关系数平方的均值作为指标Xi的信息可替代性,反映指标Xi蕴含的信息被其余指标可替代的程度。在此基础上,提出通过指标集内全部指标信息可替代性的平均值,反映指标集内各个指标的信息能被其余指标替代的平均程度。从而,提出了信息可替代性指标筛选标准,剔除了信息可替代性大于平均信息可替代性的指标,降低了待筛指标集的整体信息重叠,克服了现有研究仅仅基于两两指标间的相关程度无法有效降低指标集整体信息重叠的不足。同时,通过借鉴主成分分析筛选主成分的累计方差贡献率的思想,基于指标的相对离散系数提出了累计信息贡献率的概念,反映信息含量较大的指标占全部待筛选指标信息含量的比例。进而,根据提出的累计信息贡献率指标筛选标准剔除信息含量明显偏小的指标,克服现有研究单独使用相对离散系数无法筛选指标的不足。此外,通过提出显著再相关的指标筛选标准,明确了应先剔除对评价结果影响弱的指标再剔除信息重叠程度高的指标的筛选次序,弥补了现有研究在这一方面的匮乏。
二、指标筛选原理
(一)基于信息可替代性的指标筛选
1.指标信息可替代性的测度。针对指标初筛后保留下来的指标,通过一个指标Xi与其余指标的相关系数平方和的均值,反映指标Xi与其它指标构成的指标集间的信息重叠程度,并称其为指标Xi的信息可替代性。
2.通过信息可替代性指标筛选标准剔除对评价结果影响弱的指标。指标Xi的信息可替代性越大,指标Xi与其余全部指标间的信息重叠程度就越高,指标Xi所反映的信息越容易被其余指标构成的指标集所蕴含的信息替代,指标Xi越应予以剔除;反之亦然。通过剔除信息可替代性大于全部指标平均信息可替代性的指标,减低评价指标集间的信息重叠程度,克服现有研究仅利用两个指标间的相关性而不是一个指标与其余全部指标间的相关性遴选指标的不足。这便是信息可替代性指标筛选标准。
(二)基于累计信息贡献率的指标初筛
1.指标信息含量的测度。指标Xi的相对离散系数Ci是指标Xi的样本标准差与样本均值的比值,代表了指标Xi取值变异程度的大小,称其为指标的信息含量[13]。信息含量Ci越小,说明该指标蕴含的信息越少,对综合评价结果影响越弱,指标Xi越应予以剔除;反之,一个指标信息含量越大,该指标蕴含的信息越多,对评价结果影响越显著,该指标越应予以保留。
2.通过累计信息贡献率标准实现指标的初筛。在确定了指标信息含量的基础上,借用主成分分析筛选信息含量较大的主成分的思想[15],通过几个较大的指标的信息含量之和与全部指标的信息含量之和构建指标的累计信息贡献率,并借此剔除信息含量明显偏小的指标实现指标的筛选,保证保留下来的指标皆对评价结果影响显著,克服现有研究单独使用相对离散系数无法删除指标的不足。这便是累计信息贡献率指标筛选标准。
(三)显著再相关的指标筛选标准
剔除反映信息重叠的部分指标与剔除对评价结果影响弱的指标,是目前较为流行的两类指标筛选方法。仅通过剔除反映信息重叠的部分指标进行指标筛选的方法并不合理,很有可能存在这样的情形:保留下来的一个评价指标的信息与其它指标反映的信息少有重叠。但是这个指标所蕴含的有价值的信息很可能是全部指标中最少的一个,很可能是对评价结果影响最不显著的一个。因此,剔除反映信息重叠的部分指标并不能保证保留下来的评价指标对评价结果有显著的影响。因此,在指标筛选的实践中必须将剔除反映信息重叠的部分指标与剔除对评价结果影响弱的指标这两类指标筛选方法组合使用。这就涉及到两类方法在组合运用中先后顺序的问题。
在应该优先剔除反映信息重叠的部分指标还是优先剔除对评价结果影响较弱指标的问题上,目前尚无相关研究成果可供借鉴。不过,不难理解的是应优先剔除对评价结果弱的指标。因为,纵使一个指标与其它指标信息重叠程度再低,但是如果对评价结果影响弱也是没有意义的。如果先剔除反映信息重叠的指标极有可能保留过多对评价结果影响较弱的指标,徒然增加剔除对评价结果影响弱的指标的不确定性。反之,则不存在这样的弊端。因此,我们认为这两类指标筛选方法的组合运用遵循如下的逻辑顺序为好:先剔除对评价结果影响不显著的指标,再剔除反映信息重叠的部分指标,顺序不可颠倒。这便是显著再相关的指标筛选标准。
三、指标的筛选模型
依据显著再相关的指标筛选标准,先基于累计信息贡献率剔除对评价结果影响较弱的指标,再利用指标的信息可替代性剔除反映信息重叠的部分指标。本文方法不受指标单位不同的影响。同时由于本方法仅是进行指标的筛选不进行综合评价,从而亦不受指标正、负向问题的影响。基于这两点,在指标筛选过程中无需进行标准化处理,只需指标原始数据即可。
(一)基于累计信息贡献率的筛选方法
步骤1计算指标Xi的信息含量Ci(i=1, 2, ..., n),即指标Xi的相对离散系数。其计算公式为:
(1)
信息含量Ci表示指标Xi的信息蕴含量的大小,反映了该指标对综合评价结果影响的大小。
步骤2将指标按照信息含量由大至小的顺序进行排序。假设全部n个原始指标X1, X2, …, Xn按照信息含量由大至小顺序排序后为Xn1, Xn2, …, Xnn。其中Xni是全部n个原始指标中信息含量第i大的。
步骤3计算累计信息贡献率rp,即信息含量较大的前p个指标Xn1, Xn2, …, Xnp占全部n个指标信息含量的比重之和,即:
(2)
步骤4信息含量大的指标的筛选。若:
rp≥r0>rp-1
(3)
则保留信息含量较大的前p个指标,剔除其余指标。
主成分分析理论在筛选主成分时通常保留累计方差贡献率达到85%以上的信息含量比较大的主成分[15],以反映原始指标集的绝大多数信息。借此思想,我们保留信息含量较大且累计信息贡献率在r0=85%以上的p个指标,以保证原始指标集的信息仅有少量丢失。
(二)基于信息可替代性的指标筛选方法
步骤5计算全部p个指标之间的Person相关系数矩阵R=(rij)p×p。Person相关系数计算公式为:
(4)

步骤6计算指标Xi的信息可替代性Ri(i=1, 2, …, p),即p个指标中的一个指标Xi与其余p-1个指标构成的子类Di,(p-1)间的相关度[15]192-215:
(5)
信息可替代性Ri的构建,借鉴了聚类分析最常用的测度两指标集间相似性的类平均法的思想,它是指标Xi与其余p-1个指标构成的指标集合Di,(p-1)内每个指标间的相关系数平方的均值。它反映了指标Xi所反映的信息被其余p-1个指标可替代的程度,是对指标Xi所反映的信息的独特性价值的大小的度量。Ri越大,说明指标Xi所反映的信息越可以被其余p-1个指标反映的信息所代替;反之,Ri越小,说明指标Xi所反映的信息越不能够被其余p-1个指标反映的信息所代替,指标Xi越重要。
(6)


(7)
则删除指标Xi(i=1, 2, …, p),保留其余指标。
四、实例分析
(一)数据来源
实例中采用了包括“R&D经费支出占GDP比重”等反映大连市科技发展水平的14个指标,列于表1第2和第4列。这14个指标2000-2013年的数据来源于大连统计年鉴(2001-2014)[16]。

表1 实例指标
(二)指标的筛选
1. 基于累计信息贡献率的指标筛选
步骤1计算指标Xi的信息含量Ci。将各指标数据构成的矩阵代入式(1),得到指标Xi的信息含量Ci(i=1, 2, …, 14),列于表2第2列。
步骤2指标信息含量的排序。将表2第2列指标信息含量数据按照由大至小的顺序排序后列于表2第3列。
步骤3计算累计信息贡献率rp。将表2第3列的数据依次代入式(2),得到各指标累计信息贡献率rp(p=1, 2, …, 14),列于表2第5列。
步骤4确定暂时保留的指标。由表2第5列可知表2第4列前9个指标的累计信息贡献率r9=87.781%,刚好满足式(3)。因此根据累计信息贡献率指标筛选标准,保留表2第4列前9个指标,删除后5个指标。初筛后,指标暂时被保留的具体情况列于表2第6列。
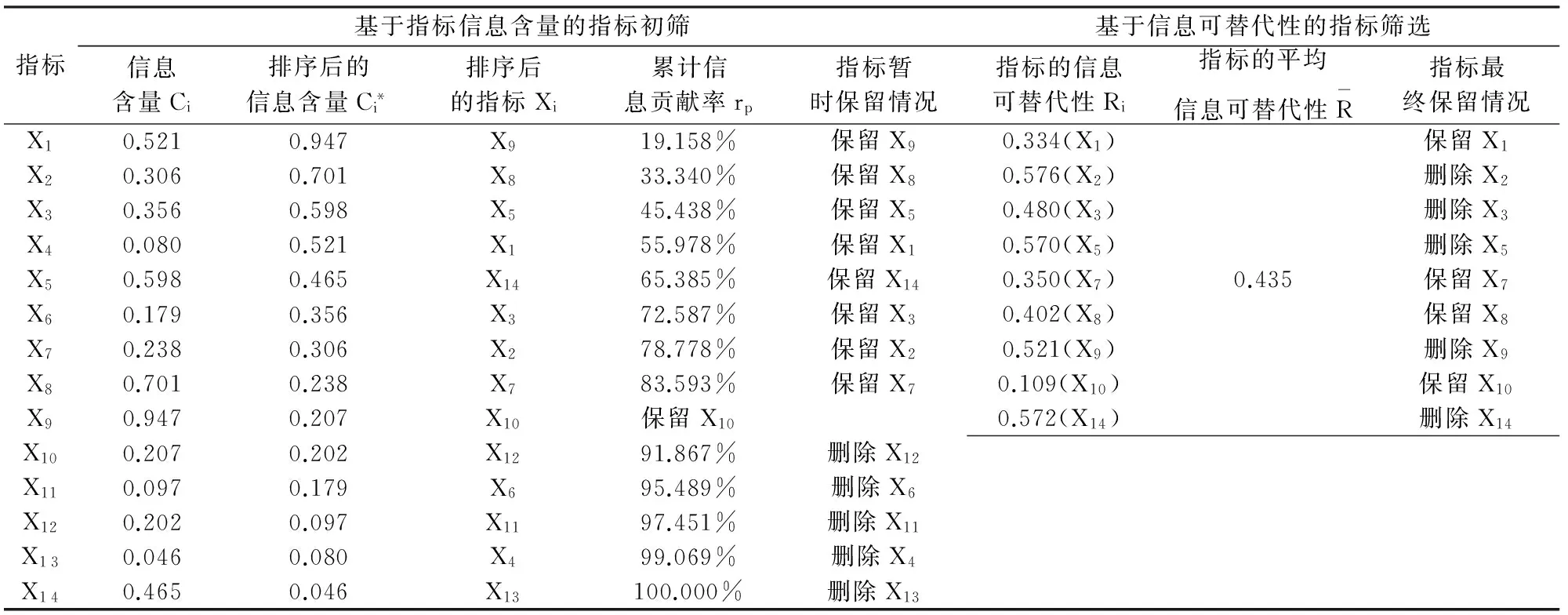
表2 指标的筛选
2.基于信息可替代性的指标筛选
步骤5计算暂时被保留下来的全部指标的Person相关系数矩阵。将暂时保留下来的9个指标的原始数据代入式(4),得到相关系数矩阵R=(rij)9×9,列于表4第2~10列。表4中相关系数绝对值普遍较大,说明指标间存在较高的信息重叠。因此,应降低指标间的信息重叠,避免重叠信息在综合评价中被过分强调。
步骤6计算指标Xi的信息可替代性Ri。将表3第2~10列除对角线上的元素“1”以外的数据分别代入式(6),得到9个暂时保留指标Xi(i=1, 2, 3, 5, 7, 8, 9, 10, 14)的信息可替代性,分别记为Rj(j=1, 2, …, 9),列于表2第7列。同时,将与信息可替代性Rj对应的指标列于表2第7列的括号内。以表2第7列的第5行的“0.350(X7)”为例,它表示指标X7的信息可替代性为0.350。

表3 相关系数矩阵R
五、结束语
通过显著再相关的指标筛选标准确定了指标筛选方法的组合顺序:先剔除对评价结果影响弱的指标,再剔除信息重叠程度高的部分指标。该标准弥补了现有研究缺乏相关标准的不足。通过借鉴主成分分析理论保留主成分的思想,基于指标的相对离散系数提出累计信息贡献率指标筛选标准,并以此标准剔除对评价结果影响较弱的指标,克服了现有研究仅仅使用相对离散系数难以实现指标筛选功能的不足。
通过测度一个指标与其它指标构成的指标集间反映信息的重叠程度,提出了基于信息可替代性指标筛选标准。指标的信息可替代性越大,说明该指标与其余指标反映的信息重叠程度越大,越可被其余指标所替代,越应予以剔除。反之亦然。通过删除信息可替代性大的指标,保证了最终保留下来的评价指标间反映信息重叠程度比较低,克服了现有研究仅仅基于两两指标间的信息重叠无法有效降低指标集信息重叠的不足。最后,以反映城市科技发展水平的14个指标的筛选为例说明了本文方法的可行性。
[1]Mitra P, Murthy C A, Pal S K. Unsupervised Feature Selection Using Feature Similarity [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(3).
[2]韩伯棠, 王莹. 中国科技人力资源评价指标体系构建方法研究 [J]. 北京理工大学学报:社会科学版, 2006, 8(6).
[3]迟国泰, 陈洪海. 基于信息敏感性的指标筛选与赋权方法研究 [J]. 科研管理, 2016, 37(1).
[4]范雪莉, 冯海泓, 原猛. 基于互信息的主成分分析特征选择算法 [J]. 控制与决策, 2013, 28(6).
[5]Peng H, Long F, Ding C. Feature Selection Based on Mutual Information: Criteria of Max-dependency, Max-relevance, and Min-redundancy [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(8).
[6]Hild K E, Erdogmus D, Torkkola K, et al. Feature Extraction Using Information-theoretic Learning [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006, 28(9).
[7]Meyer P E,Schretter C, Bontempi G. Information-theoretic Feature Selection in Microarray Data Using Variable Complementarity [J]. IEEE Journal of Selected Topics in Signal Processing, 2008, 2(3).
[8]Estevez P A,Tesmer M, Perez C A, et al. Normalized Mutual Information Feature Selection [J]. IEEE Transactions on Neural Networks, 2009, 20(2).
[9]何绍荣, 梁金明, 何志勇. 基于互信息和关系积理论的特征选择方法 [J]. 计算机工程, 2010, 36(13).
[10]裘国永, 王娜, 汪万紫. 基于互信息和遗传算法的两阶段特征选择方法 [J]. 计算机应用研究, 2012, 29(8).
[11]顾雪松, 迟国泰, 程鹤. 基于聚类-因子分析的科技评价指标体系构建 [J]. 科学学研究, 2010, 28(4).
[12]周立斌, 李刚, 迟国泰. 基于R聚类-变异系数分析的人的全面发展评价指标体系构建 [J]. 系统工程, 2010, 28(12).
[13]石宝峰, 迟国泰. 基于信息含量最大的绿色产业评价指标筛选模型及应用 [J]. 系统工程理论与实践, 2014, 34(7).
[14]刘靖明, 韩丽川, 侯立文. 基于粒子群的K均值聚类算法 [J]. 系统工程理论与实践, 2005, (6).
[15]汪冬华. 多元统计分析与SPSS应用 [M]. 上海: 华东理工大学出版社, 2010.
[16]大连市统计局, 国家统计局大连调查队. 大连统计年鉴 [M]. 北京: 中国统计出版社, 2001-2014.
(责任编辑:马慧)
Study of Evaluation Indices Screening based on Information Substitutability
CHEN Hong-hai
(School of Finance, Nanjing University of Finance and Economics, Nanjing 210023, China)
An indices screening method is proposed for screening indicators of impact on the evaluation results significantly and indicators with low information overlap. The coefficient of variation of an indicator is used as its information content. According to the proposed standard of accumulative information contribution rate to delete the indices with significantly smaller information content in the initial screening indices. And this method overcomes the defect that only using coefficient of variation is unable to screen indices. This paper takes the ideas of cluster analysis, uses the mean value of Person correlation coefficient squared between an index and the other all indices to reflect the degree that information of the index can be replaced all other indicators. The indices with the greater information substitutability are deleted based on the standard of information substitutability. This guarantees that the information overlap degree among the final reserved indices is low, and overcomes the deficiency that the existing research is difficult to reduce information overlap effectively of an evaluation indices set only by means of the correlation between any two indices. In addition, deleting indicators with high information overlap and deleting indices of impact on the evaluation results weakly should all be carried out, but there is a problem of what priority. In order to solve this problem, the significance-correlation standard is proposed. Finally, a numerical illustration is presented to illustrate the effectiveness of the indices screening method.
evaluation index; indices screening; information substitutability; information overlap
2015-11-09;
2016-03-20
国家自然科学基金项目《基于违约风险金字塔原理的小企业贷款定价模型》(71171031);国家自然科学基金项目《基于存量与增量叠加风险控制的全资产负债优化模型》(71471027)
陈洪海,男,辽宁辽中人,金融工程博士,研究方向:复杂系统评价。
F222.3∶C829.22
A
1007-3116(2016)10-0017-06

