基于均衡关系的中国人口死亡率预测模型
柳向东,范洋洋
(暨南大学 经济学院, 广东 广州 510632)
【统计理论与方法】
基于均衡关系的中国人口死亡率预测模型
柳向东,范洋洋
(暨南大学 经济学院, 广东 广州 510632)
人口死亡率反映了人口的死亡程度,准确预测死亡率是人口科学及人口经济学研究的重点之一,同时也是长寿风险测量的重要数据基础。基于Lee-Carter模型,探索中国大陆与台湾地区死亡率的相关性,通过协整分析考虑两地死亡率的长期均衡关系,创新性地建立基于相关性的向量误差修正模型(VECM),克服传统自回归移动平均模型(ARIMA)使用有限数据进行预测的局限性;均方预测误差作为检验标准,结果表明:基于VECM模型的预测效果比传统的预测效果更佳;基于中国大陆地区和台湾地区的死亡率长期均衡关系,可以为两地联合长寿债券的定价提供重要参考。
死亡率预测;Lee-Carter模型;长期均衡关系;死亡率相关性;误差修正模型
一、引 言
人口死亡率是衡量一定规模人口每单位时间的死亡数目,反映人口的死亡程度,与人口健康状况、人口质量密切相关,也直接影响人口结构,是人口科学及人口经济学研究的重点,同时也能为长寿风险识别和量化提供重要的数据基础。随着社会经济的发展、医学的进步和公共卫生新技术的应用以及教育水平的提升,中国人口死亡率呈长期下降趋势,人均寿命的延长使人口老龄化程度不断加剧,从而使得政府在制定养老相关政策、人寿保险精算行业在寿险产品的定价、企业的养老金计划以及个人的退休计划等方面都面临着巨大的压力。科学、准确地预测未来人口死亡率能有效地识别和量化长寿风险,对政府、企业及个人都有重要指导意义。
近年来,死亡率模型中广受推崇的是Lee和Carter提出的Lee-Carter模型[1]。该模型考虑了死亡率的动态性,各参数的意义明确直观,简单易懂,在实际问题中应用性较强。之后,根据各国人口死亡率的不同特征,不少学者对Lee-Carter模型进行了扩展改进。在国外,Brouhns等针对分年龄分性别的死亡率预测问题,在Lee-Carter模型中嵌入泊松回归模型[2];Czado等建立了对数双线性泊松回归模型,并采用贝叶斯估计对死亡率进行了预测[3];Delwarde等提出了不同的统计方法对Lee-Carter模型的三个参数进行估计[4];Renshaw等将两个相依的时期效应引入Lee-Carter模型,提出了多因素死亡率模型,并于2006年提出了考虑出生年效应的随机死亡率模型[5-6]。在国内,Lee-Carter模型及其各种扩展形式也同样被学者使用并拓展。黄顺林等运用基于出生年效应的Lee-Carter模型对中国男性人口死亡率数据进行拟合,并将预测结果用于养老金系数的估计[7];李志生等基于中国人口死亡率数据得出了加权最小二乘法是估计Lee-Carter模型参数的最佳方法[8];王晓军等利用贝叶斯信息准则、似然比检验,比较各随机死亡率模型,结果表明Carins-Blake-Dowd两因素模型的一个扩展模型的拟合效果最优[9];有学者针对中国有限数据且存在缺失的情况,采用“双随机过程”进行建模;还有学者使用函数型方法分析了中国人口数据,并建立函数型死亡概率预测模型对未来死亡率进行了预测。
针对中国大陆人口死亡率数据,Lee-Carter模型的各种扩展形式也没能更多地挖掘出死亡率数据中包含的信息。Yang等基于Lee-Carter模型建立了多国死亡率连贯模型来对死亡率进行预测[10];Yang等又通过协整分析找到美国和英国人口死亡率的相关性,并建立了多国人口死亡率预测模型对长寿债券进行定价[11]。在多国或多地区背景下,利用死亡率的相关性建立死亡率预测模型能够更多地挖掘并利用死亡率历史数据中的信息,而协整分析能够找到多国或地区之间死亡率的长期均衡关系。段白鸽针对台湾地区充足死亡率数据和大陆地区有限死亡率数据,展现出大陆地区和台湾地区未来人口死亡率呈现趋同化发展的现象[12]。
本文基于经典的Lee-Carter模型,探索研究中国大陆地区与台湾地区人口死亡率的相关性,以两地区死亡率残差的差分进行相关性的描述,并通过协整分析找出两地区死亡率的长期均衡关系,创新地建立基于相关性的误差修正模型(VECM)对未来死亡率进行预测,并与基于传统ARIMA模型对死亡率的预测效果进行比对,从而得到更加精准的死亡率预测模型。
二、基于Lee-Carter模型的死亡率预测模型
(一)Lee-Carter模型
Lee-Carter模型结构如下:
lnmx,t=ax+bxkt+ex,t
(1)

利用最小二乘法对参数进行估计时,由于参数kt和bx是通过先后两步分别进行估计得到的,即使对模型求解的时候使用的是死亡率的对数,也并不需要对kt的估计值进行调整。
(二)基于台湾地区相关性的死亡率模型
国内学者在进行死亡率预测的过程中,往往将其单纯地建立在国家的原始数据上,他们尝试最大化地利用这些原始数据的信息,但是由于中国大陆地区数据的有限性,使死亡率预测存在一定的局限性。Yang提出国与国之间的死亡率也存在一定的关系,并画出了英国66岁、76岁、86岁、96岁女性人口死亡率与65岁以上年龄段的英国男性以及美国女性与美国男性的相关性图,这将引导我们对于国家与国家、地区与地区之间死亡率相关性问题进行探索。本文以中国大陆地区与台湾地区人口死亡率的相关性作为脉络,探讨考虑相关性与不考虑相关性的死亡率预测效果的变化情况。
1.关于相关性人口死亡率模型的建立。参考对多国相关模型的探讨,建立考虑与其他地区死亡率有相关性的死亡率模型:
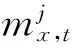
(2)
这里用矩阵的形式更加清晰地表示基于多个国家或地区相关性的死亡率预测模型:

(3)

(4)

(5)

2.建立关于Kt的VECM模型。对于经典的Lee-Carter模型或者其扩展模型,一般是采用ARIMA模型对时间序列Kt进行预测。然而,考虑到本文利用大陆地区与台湾地区人口死亡率的相关性,传统的ARIMA模型将不再适用,这里将创新性地建立基于相关性的VECM模型对Kt进一步预测。在建模之前,首先要通过单位根检验来看序列之间是否能够进行协整分析;其次再在结果的基础上进行协整分析来了解国家或地区之间是否存在一个共同的变化趋势,即长期均衡关系;最后根据分析结果构建合适的基于相关性的VECM模型。
协整分析要求Kt中每一个子序列都是非平稳的,并且都满足I(p)过程,即存在p个单位根。Kt的p阶VECM模型可以表示为:
(6)

为了便于后面的推导,本文将VECM模型整理为VAR模型如下:
(7)

由于VECM模型中的残差项εt与Lee-Carter模型中的残差差分项Δex,t是相互独立的,进而可以得到Kt+n+1的公式:
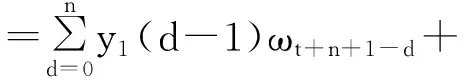
(8)
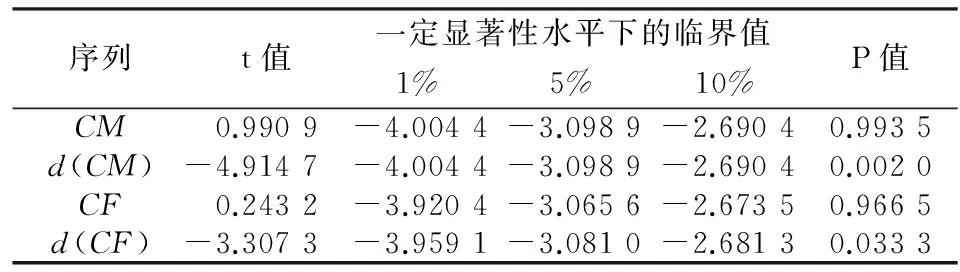
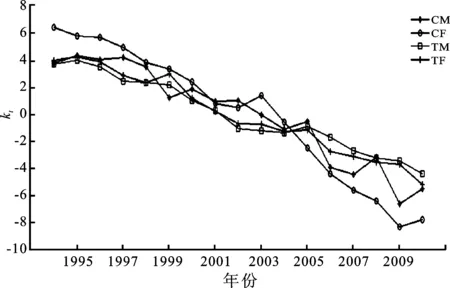
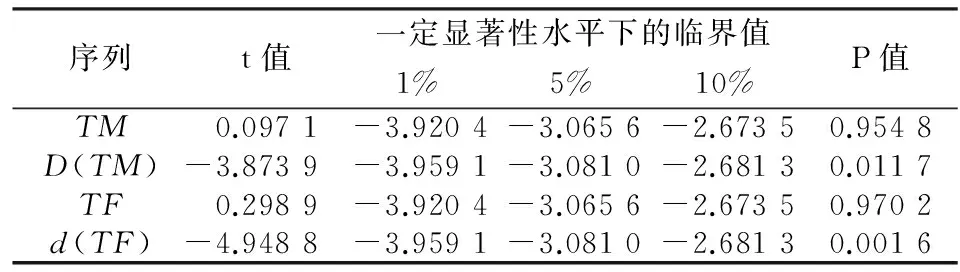
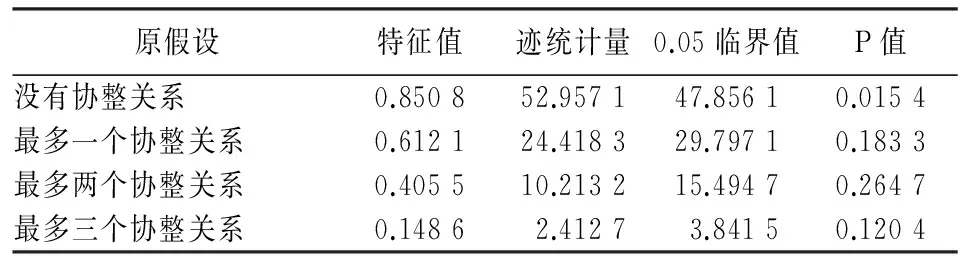
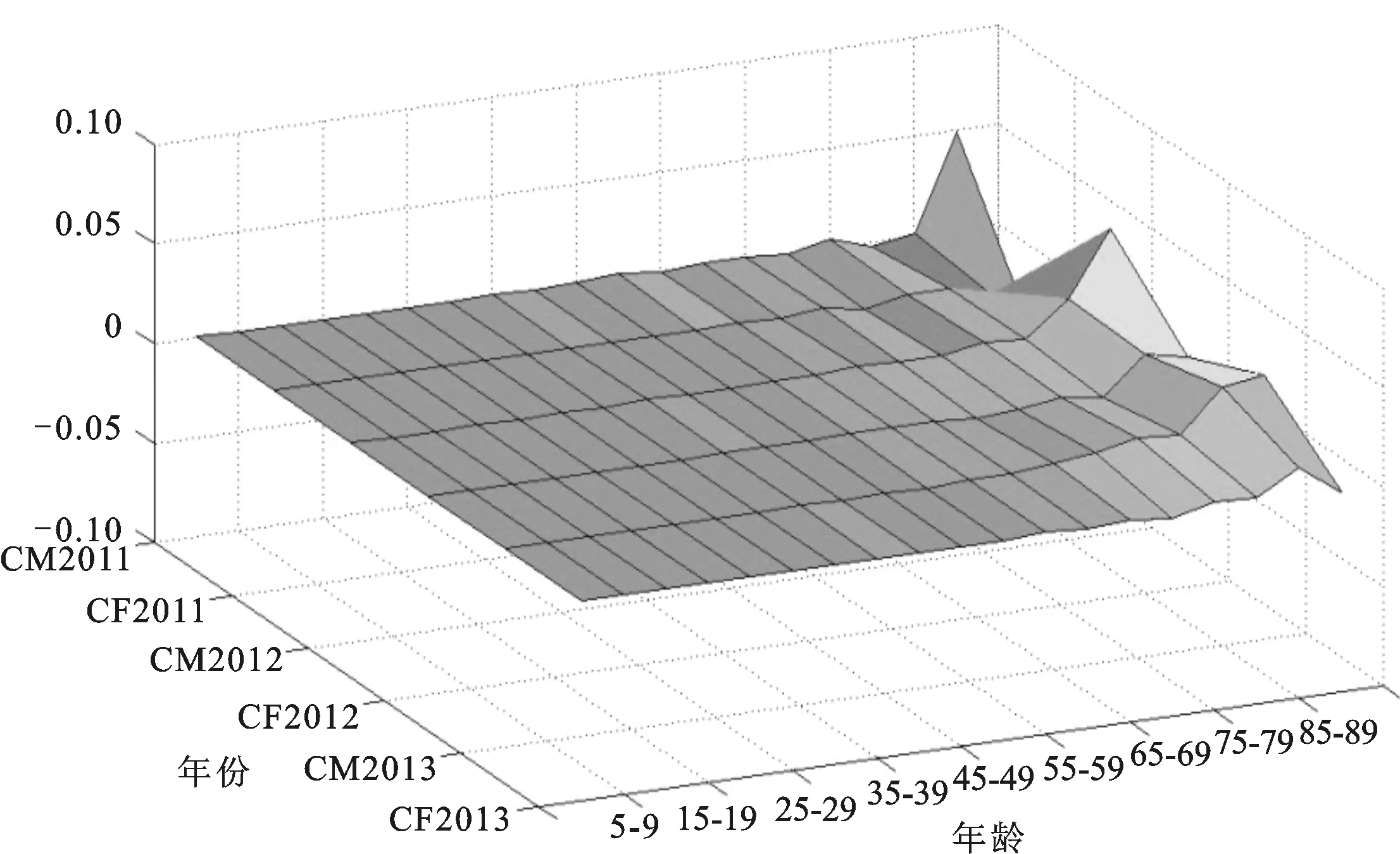
其中yd(h)=y1(h-1)φd+1(d (d=1,2,…,p;h=1,2,…,n) (h=1,2,…,n) y1(-1)=I2Nθ0(0)=I2Nyi(0)=φi (i=1,2,…,p) 3.考虑国家或地区相关性的人口死亡率预测模型。根据方程(2),可以得到以下的差分方程: lnMx,t+n+1-lnMx,t =bx(Kt+n+1-Kt)+ex,t+n+1-ex,t (9) 整合方程(8)和方程(9)可得: (10) (11) (n=1,2,…,T;j=1,2,…,2N) (12) (13) 中国大陆地区所采用的原始数据是1994—2014年全国人口分性别、分性别死亡率的数据。1994—2006年的数据来自《中国人口统计年鉴》,2007—2014年数据来自《中国人口与就业统计年鉴》,其中2000年的数据来自《第五次人口普查数据》,2010年数据来自《2010年人口普查资料》。本文以5岁为一个年龄段对死亡率进行分组计算,年龄段分为0~4岁、5~9岁、10~14岁、…、80~84岁、85~89岁、90岁以上,一共19组。对于原始数据需要进行以下处理:1995年、2000年、2005年、2010年数据年龄均截至100岁,需要将90岁以上人口数量合并到一组重新计算人口死亡率;1996年末组年龄截至85岁,对85~90岁以及90岁以上这两个年龄组采用相邻年份同组死亡率均值补齐。对于台湾地区,其原始数据来源于人类死亡率数据库(Human Mortality Database, HMD),选择了1994—2010年以5年为一个年龄段的死亡率数据。由于数据需要与中国大陆地区数据相一致,所以需对台湾地区数据进行合理处理。首先,将台湾地区0岁人口的死亡率与1~4岁人口的死亡率合并到一个分组,成为0~4岁年龄组;其次,由于台湾地区人口死亡率在90岁以上统计均有五个分组,分别为90~94岁、95~99岁、100~104岁、105~109以及110+,最后将这五组的人口死亡率合并成一组为90岁及以上人口死亡率。死亡率的合并是由公式mx,t=(Dx,t/Ex,t)计算得到,其中Dx,t为x岁的人在时间t的死亡人数,Ex,t为x岁的人在时间t的风险暴露人数。 (一)传统人口死亡率模型预测 传统的死亡率预测模型是仅以本国或本地区死亡率数据为依据,基于ARIMA模型对时间因子序列kt进一步预测。将中国大陆地区1994—2010年的数据带入Lee-Carter模型中,运用最小二乘估计法(OIS)得到参数ax、bx、kt的估计值。在对参数kt进行预测前首先需要对各个序列进行单位根检验,检验结果如表1。 表1 中国大陆人口死亡率时间因子序列ADF单位根检验表 注:表中序列名称CM、CF表示中国大陆男性、女性人口死亡率的时间因子序列。 从表1的结果可以看出,在一定的显著性水平下,无论男性还是女性的时间因子序列均存在单位根,而当序列在进行差分后,两个序列在5%的显著性水平下拒绝原假设,所以结果显示男性与女性的时间因子序列均为平稳序列。ADF检验结果表明两组原始序列为一阶单整序列,可以进行进一步的ARIMA模型预测。 利用R软件包中自带函数可以对序列kt进行预测。软件结果表明,最适合中国男性死亡率时间因子预测的ARIMA模型为ARIMA(1,1,0),最适合中国女性死亡率时间因子预测的ARIMA模型为ARIMA(0,1,0)。用对应的ARIMA模型对时间因子kt进行2011—2013年的预测得到表2的结果,将其带入Lee-Carter模型中便可得出人口死亡率数值。 表2 基于ARIMA模型对中国人口死亡率时间 因子kt的预测结果表 (二)考虑相关性的人口死亡率模型预测 将台湾地区的相关数据带入Lee-Carter模型中,可得出台湾地区男性与女性对于参数ax、bx、kt的估计值。结合中国大陆地区,参数ax、bx、kt估计值表示如图1。 图1 参数ax、bx、kt的估计值图 参数ax为死亡率的水平指数,可以看出参数估计曲线呈浴盆状:在0~4岁组及高年龄组较高,这与现实的情况相符,因现实生活中婴儿抵抗力较低,所以在婴幼儿阶段死亡率较高;随着抵抗力及成长力的加强,死亡率跟随下降,并在10~14岁组死亡率达到最低,因为这段时期生命成长的力量非常强大;此段时期过后,由于人的成长力逐渐减小,受外界各种因素及生命生长机理的影响,随着年龄的不断增加,死亡率呈现递增趋势。另一方面,无论是从大陆地区还是台湾地区的模拟趋势,均可知女性的死亡率水平指数低于男性。 对于bx,大陆及台湾地区的大体趋势是相同的,由于数据量较少在拟合后有些波动,在低年龄组人口的bx值较高,在年龄较小时,排除自身生命发展的影响,对死亡率水平指数的变化都比较敏感;而在高年龄组中bx取值比较稳定,并有趋于0的趋势,这主要是因为高年龄组人口的实际死亡率对死亡率水平指数的变化并不敏感;而分性别对比,男性在高年龄组的敏感度比女性大,说明男性人口结构变化会比女性更加显著。 参数kt估计值随着年份增加呈现向下倾斜的趋势,表明中国人口死亡率随着时间的推移在不断减小,从趋势上可以看出基本呈线性,说明整体减小的速度也较为稳定;在性别上,1994年女性的估计值要大于男性,但随着年份推移,直至2010年,女性的估计值均小于男性,表明女性死亡率的减小速率大于男性的速率。 表3 台湾地区人口死亡率时间因子序列ADF单位根检验表 注:TM、TF表示中国男性、女性人口死亡率的时间因子序列。 在确定模型正确的滞后阶数时,本文用了三个标准,分别为Log-likehood、AIC(AkaikeInformationCriterion)、SBC(SchwarzBayesianCriterion),这三个准则均要求数值越小则模型越好。鉴于采用的历史数据年份相对较少,这里只能在滞后一阶以及滞后二阶中进行选择,结果如表4。三种准则下均是滞后一阶的效果更好,在滞后一阶时的数值均比滞后二阶时的数值小,故对于误差修正模型(VECM)来说,最佳滞后的阶数为一阶。 表4 最佳滞后阶数确定表 通过ADF检验确定中国大陆地区及台湾地区时间因子序列均为I(1)序列,满足协整检验的前提,表5是对四组时间因子序列进行Johansen迹统计量检验的结果。在原假设为没有协整关系时,从Johansen检验结果可以看出,在该假设下计算的迹统计量为52.957 1,大于临界值47.856 1且概率P值为0.015 4,可以拒绝该原假设,认为至少存在一个协整关系;同理,对于下一个原假设,最多存在一个协整关系,在该假设下的迹统计量值为24.418 3,小于临界值29.797 1且P值为0.183 3,这时不能拒绝该原假设,从这两个假设中可以得到序列间存在一个协整关系。 表5 Johansen协整检验表 根据中国大陆地区及台湾地区人口死亡率的时间因子序列,可以得到式(14)的VECM(1)模型,即: (14) 利用误差修正模型(VECM)对时间因子kt在2011—2013年的预测值见表6。 表6 基于VECM模型对中国人口死亡率时间 因子kt的预测结果表 由于本文针对中国数据确定的误差修正模型为VECM(1),故p=1带入式(6)、(7)、(8)可得:φ1=Π+I4,θ1(1)=y1(0)=φ1,θ2(2)=y1(0)φ1=φ12,…,θn(n)=φ1n,从而将推导式及通过VECM(1)模型得到的结果带入式(10)、(11)、(12)、(13),可得到中国大陆男性及女性分年龄段的人口死亡率。 (三)基于VECM模型预测残差分析 对模型预测结果进行残差分析能够检验模型的拟合效果。图2给出了中国大陆2011—2013年男性及女性分年龄段模型拟合残差图。从三维立体图来看,在年龄变化趋势上,死亡率预测残差在0~4岁至80~84岁年龄组几乎为0,而在85~90岁及90岁+年龄组女性死亡率预测残差也基本为0,但男性的残差值有少许波动;在年份变化上,同一年龄没有明显的变化趋势,高年龄段的个别年龄变动存在不确定性,本文在高年龄组也是按照5岁一个年龄段进行预测的,这样会使高年龄组相对于低年龄组的残差值较大。从总体上,拟合残差在年龄和年份变化上没有明显的变动趋势,这也表明残差的独立性。 图2 基于VECM模型的预测残差图 (四)模型预测效果的分析比较 为了得到死亡率相关性在死亡率预测过程中对预测效果的影响,本文用两种模型预测出的2011—2013年的死亡率分别与这三年的实际人口死亡率作对比,对比结果见表7。以最小均方预测误差(MSPE)作为模型好坏的评判标准,均方预测误差为: (15) 将模型预测结果与实际值带入式(15)中,得到的结果如表7。除2011年中国大陆女性的预测结果ARIMA模型预测的误差稍小以外,结果表示考虑相关性后用VECM模型的预测结果的均方误差比不考虑相关性低,特别对于2012年,VECM模型的预测比ARIMA模型的预测效果好很多,而且各年份女性死亡率的预测效果要略好于男性,这说明在总体上考虑相关性的人口死亡率预测方法要优于传统基于ARIMA模型的预测方法。 表7 模型均方预测误差对比结果表 考虑死亡率之间的相关性可以大大增加对死亡率数据中相关信息的利用率。基于中国人口死亡率的有限性,如果只单纯以本国数据为基础,尝试各种新的随机模型形式以增加模型的复杂性,也不能挖掘出数据中更多的信息,因为依据的数据量有限。 将中国大陆地区的死亡率数据与台湾地区的死亡率数据相结合,运用最小二乘法对Lee-Carter模型参数进行拟合估计,并通过协整分析创新地建立基于相关性的VECM模型,探讨分析死亡率之间的相关性,并找出长期均衡关系,得到基于相关性的未来人口死亡率的预测值;为了验证相关性对预测效果的影响,运用2010年之前的数据对2011—2013年的数据进行预测,并与在未考虑相关性下运用传统ARIMA模型进行预测的效果进行对比,以均方预测误差作为模型检验的标准,表明基于长期均衡关系的预测结果更好;相比于传统的方法,基于相关性及均衡关系预测方法不仅能利用中国分年龄分性别死亡率数据给出更可信的预测效果,而且预测结果还清晰地表明中国人口死亡率呈现浴盆状特征,无论男性还是女性都存在一个稳定的下降趋势,而在下降速率上女性显著高于男性呈现一个更稳定的状态。然而,本文在分年龄方面,以5岁为一个年龄组,这使对高年龄段的预测会受到一定影响,如果考虑单个年龄的死亡率预测,也许更能清晰地说明基于死亡率相关性的预测模型更优。 相关性能有效地弥补死亡率数据的局限性,使其预测效果更为准确,而在死亡率预测过程中求得的相关性可以继续应用于基于两地的长寿风险债券的定价问题上。死亡率持续下降的趋势值得深层次的研究,在未来,通过两地区死亡率的相关性可以预测生存概率,可以进一步制作生命表,并对新生儿的预期寿命进行预测,也可以应用到长寿风险的深层次探讨中。 [1]LeeRD,Carter,LR.ModelingandForecastingUSMortality[J].JournaloftheAmericanStatisticalAssociation, 1992, 87(419). [2]BrouhnsN,DenuitM,VermuntJK.APoissonlog-BilinearRegressionApproachtotheConstructionofProjectedLifetables[J].Insurance:MathematicsandEconomics, 2002, 31(3). [3]CzadoCDelwardeA,DenuitM.BayesianPoissonLog-bilinearMortalityProjections[J].Insurance:MathematicsandEconomics, 2005, 36 (3). [4]DelwardeA,DenuitM,PartratC.NegativeBinomialVersionoftheLee-CarterModelforMortalityForecasting[J].AppliedStochasticModelsinBusinessandIndustry, 2007, 23(5). [5]RenshawAE,HabermanS.Lee-CarterMortalityForecastingwithAge-specificEnhancement[J].Insurance:MathematicsandEconomics, 2003, 33 (2). [6]RenshawA,HabermanS.ACohort-basedExtensiontotheLee-CarterModelforMortalityReductionFactors[J].Insurance:MathematicsandEconomics, 2006, 38(3). [7]黄顺林,王晓军.加入出生年效应的死亡率预测及其在年金系数估计中的应用[J]. 统计与信息论坛, 2010(5). [8]李志生,刘恒甲.Lee-Carter死亡率模型的估计与应用 [J]. 中国人口科学, 2010(3). [9]王晓军,黄顺林. 中国人口死亡率随机预测模型的比较与选择[J]. 人口与经济, 2011 (1). [10]YangSS,YueJC,YehYY.CoherentMortalityModelingforaGroupofPopulations[C]∥Livingto100Symposium,2011. [11]YangSS,Chou-WenWang.PricingandSecuritizationofMulti-countryLongevityRiskwithMortalityDependence[J].Insurance:MathematicsandEconomics, 2013, 52(2). [12]段白鸽. 中国全年龄段人口平均预期寿命的动态演变[J]. 人口与经济, 2015(1). (责任编辑:郭诗梦) Mortality Forecasting for China Based on the Long-run Equilibrium Relations LIU Xiang-dong, FAN Yang-yang (Department of Statistics, School of Economics, Jinan University, Guangzhou 510632, China) Human mortality rates, which reflect the extent of deaths, are one of the key researches of Population Science and Population Economics. Accurately mortality forecasts are also the significant data for the measurement of longevity risk. Based on Lee-Carter model, this paper considers mortality correlations and the long-run equilibrium of mortality rates between China mainland and Taiwan province for mortality forecasts, and innovatively proposes a VECM model based on the correlations which differs from the traditional ARIMA model that is only based on the limited information of mortality data. The method of the minimum mean square prediction errors (MSPE) is used for criteria. Our results show that the forecasting based on the VECM model is better than traditional Lee-Carter model. Mortality rates between China mainland and Taiwan province can also provide important reference for pricing a multi-region longevity bonds. Mortality forecasting; Lee-Carter model; long-run equilibrium; Mortality correlation; VECM model 2016-03-31;修复日期:2016-06-07 国家自然科学基金面上项目《带Levy跳的多因子市道轮换框架下的仿射利率结构研究》(71471075);教育部人文社会科学研究一般项目《基于市道轮换框架下带Levy跳的高频数据的波动率研究》(14YJAZH052);中央高校基本科研业务费专项资金资助项目(暨南跨越计划)《PMCMC算法在市道轮换框架下利率结构模型中的应用》(15JNKY003) 柳向东,男,湖南浏阳人,理学博士,教授,博士生导师,研究方向:统计学及其应用; F222.3 A 1007-3116(2016)10-0003-07 范洋洋,女,四川南充人,硕士生,研究方向:统计学及数量经济。



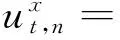

三、中国人口死亡率的预测



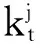
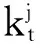




四、结 论

