多输入不确定离散系统的变结构控制
陈秀琴,赵 娜,李钧涛
(1.信阳职业技术学院数学与计算机科学学院,河南 信阳 464000;2.河南师范大学数学与信息学院,河南 新乡 453007)
多输入不确定离散系统的变结构控制
陈秀琴,赵 娜,李钧涛
(1.信阳职业技术学院数学与计算机科学学院,河南 信阳 464000;2.河南师范大学数学与信息学院,河南 新乡 453007)
目的 针对一类多输入离散不确定系统,提出一种新的变结构控制器设计。方法 利用Lyapunov理论和变结构控制理论,分析当系统参数扰动和外界扰动满足一定条件时,通过设计观测器的方法,对不确定项提出了一种新的估计,按照所设计的不确定项估计量,能够使不确定项估计误差不超过ε/(1-λ);并且当不确定项变化缓慢时,能够使观测误差趋近于零。结果 根据变结构控制理论分析,系统的抖振是难以避免的,所以如何处理不确定项是降低抖振的关键,通过设计不确定项的估计量解决了这一问题。通过选择合适的切换函数和控制器,可使系统所有状态落入一个确定的区域,特别是当不确定项变化缓慢时,闭环系统能够渐近稳定,并且可使系统抖振指数衰减至零。最后给出的仿真实例也验证了该方法的有效性。结论 给出的滑模变结构控制器可以有效地降低系统抖振,提高系统的性能。
不确定离散系统;滑模控制;不确定性估计量;抖振
0 引 言
由于离散系统的状态是严格限制在一个时间序列,不能完全发生在切换面。因此这种系统增加了控制的难度。近来,离散系统引起了学者的广泛关注,并从不同角度如切换面、干扰补偿、抖振克制等提出了多种设计方法[1-12]。尽管这些方法在某些条件约束下能改善系统的动态性能和降低抖振。但是这些方法设计较复杂且易增大系统误差。基于滑模变结构控制理论,提出了利用不确定性观测器估计外界扰动,用观测值来设计控制器的新方法,而且适当选取观测器可以使观测误差充分小。和常规方法相比,所设计的控制器能够有效降低抖振,特别是当不确定性变化缓慢时能使系统抖振指数衰减到零。最后,基于MATLAB 6.5软件对多输入离散不确定系统进行分析和数值模拟,验证了该滑模控制方法的优良性能。
1 设计不确定性估计量
考虑下面的多输入离散不确定系统:
x(k+1)=(A+ΔA)x(k)+(B+ΔB)u(k)+d(k)
(1)
其中x∈Rn是系统状态变量,u∈Rm是控制输入,A、B是已知常数矩阵,且(A,B)可控,B矩阵是满列秩,ΔA、ΔB代表参数扰动,d(k)是未知有界的外部干扰。
目的是设计滑模控制器使闭环系统在参数扰动和未知外部干扰下渐近稳定,并且降低系统抖振。
假设1ΔA、ΔB、d(k)满足以下条件:

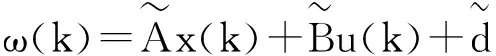
x(k+1)=Ax(k)+B(u(k)+ω(k))
(2)
x1(k+1) =A11x1(k)+A12x2(k)=A1x(k)
x2(k+1)=A21x1(k)+A22x2(k)+B2u(k)+f(k)
=A2x(k)+B2u(k)+f(k)
(3)
其中f=(k)=B2ω(k)。
根据变结构控制理论知,系统的抖振是难以避免的,所以如何处理不确定性是降低抖振的关键,下面通过设计不确定性的估计量来解决这个问题。
根据式(3),提出如下的不确定性估计量:
μ(k+1)=-λμ(k)+(λ+1)[x2(k)+A2(k)]+B2u(k)]
(4)
(5)
假设2 ‖f(k+1)-f(k)‖≤ε,其中ε>0。
推论 根据式(4)和式(5)来设计不确定性估计量,能够使不确定性估计误差不超过ε/(1-λ)。
证明 由式(3)和式(5)式得:
=(λ+1)[A2x(k)+B2u(k)+f(k)]+λμ(k)-(λ+1)[x2(k)+A2x(k)+B2u(k)]
=(λ+1)f(k)+λμ(k)-(λ+1)x2(k)
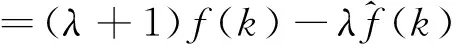
(6)



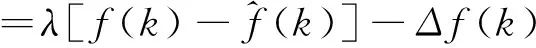
=λef(k)-Δf(k)
(7)
解方程(7)可得:
‖ef(k+1)‖≤λ‖ef(k)‖+ε≤λ2‖ef(k-1)‖+λε+ε

(8)
则

(9)
所以当k足够大时,估计误差不超过ε/(1-λ)。
如果不确定性变化缓慢,即Δf(k)≈0时,从假设2知可以取ε=0,即:


2 滑模控制设计
由式(3)得:
x1(k+1)=A11x1(k)+A12x2(k)
(10)

选择切换函数:
s(k)=[C1,I]x(k)=Cx(k)
(11)
即滑模动态为:
x1(k+1)=(A11-A12C1)x1(k)
(12)
定义边界层为:
Sδ={x(k);‖s(k)‖≤δ}
(13)
下面可以取控制器
(14)


证明 把式(14)代入式(11)得:
s(k+1)=Cx(k+1)=CAx(k)+B2u(k)+f(k)


(15)
如果系统状态在k时刻超出边界层,即,‖s(k)‖>δ,则有
s(k+1)=αs(k)-ef(k)
‖s(k+1)‖≤α‖s(k)‖+‖ef(k)‖


(16)
如果不确定性变化缓慢,即f(k)≈f(k-1),根据式(15)有
如果系统状态在k时刻超出边界层,即‖s(k)‖>δ,则有
=αs(k)=α2‖s(k-1)‖=…=αk+1‖s(0)‖
→0
(17)
因此,闭环系统所有状态将落入边界层Sδ内,并且能使系统抖振指数衰减至零。
3 数值仿真
(18)
考虑下面的不确定离散时间系统:
x(k+1)=(A+ΔA)x(k)+(B+ΔB)u(k)+d(k)

设计扰动观测器
u(k+1)=-λμ(k)+(λ+1)[x2(k)+A2(k)+B2u(k)]

图1 估计量的变化曲线图
(19)
其中f(k)=0.1x1(k)-0.2x2(k)+0.1u(k)+0.1sin(0.05k),x(0)=(4.5,-7),λ=0.1。不确定性的估计量仿真结果如图1所示,有效地显示了不确定性估计的精确度。
取切换函数为
s(k)=Cx(k)=2x1(k)+x2(k)
(20)
根据(14)设计控制器
其中α=0.5,β=0.7,δ=0.6,仿真结果如图2和图3所示。


4 讨 论
研究了一类多输入离散不确定系统的变结构控制。基于扰动观测器,给出了一种新的鲁棒变结构控制器,该控制器能够有效地降低抖振,特别是当不确定性变化非常缓慢时,可以使系统抖振指数衰减至零。
[1]孙林,郑煜,姚娟.不确定离散奇异系统的鲁棒非脆弱H∞状态反馈控制[J].山东大学学报:理学版,2011,46(01):35-41.
[2]潘海鹏,李建宁,张益波.输入受限不确定离散系统的灰色滑模控制[J].控制工程,2009,16(06):659-661.
[3]蔡国梁,周维怀,郑松,等.不确定离散系统全程滑模变结构控制[J].江苏大学学报:自然科学版,2010,24(03):363-368.
[4]徐启敏,焦贤发.不确定双线性随机离散时间系统的鲁棒控制[J].合肥工业大学学报:自然科学版,2011,34(06):949-953.
[5]梁东颖.一类不确定离散时滞系统鲁棒H∞可靠控制的设计方法[J].广西科学院学报,2013,29(02):75-79.
[6]段玉波,姚进,毕二刚,等.不确定离散系统的神经网络自适应控制方法研究[J].自动化技术与应用,2012,31(03):4-8.
[7]陈衍峰,刘维玲.具有饱和约束不确定离散系统的最优控制[J].通化师范学院学报,2010,31(10):4-5.
[8]谢立,田翔,陈耀武.不确定离散时滞系统的鲁棒H_∞弹性滤波[J].东南大学学报:自然科学版,2009,(S1):240-243.
[9]刘毅,冯佳昕,赵军.一类不确定离散切换模糊时滞系统的鲁棒输出反馈控制[J].东北大学学报:自然科学版,2009,30(01):13-16.
[10]何召兰,王茂,黄昆,等.不确定离散切换系统的滑模控制[J].控制与决策,2009,24(05):789-793.
[11]蒋诗泉,刘思峰,刘中侠,等.三次时变参数离散灰色预测模型及其性质[J].控制与决策,2016,31(02):79-86.
[12]郭继峰,高存臣.离散多时滞广义不确定系统的变结构控制[J].系统科学与数学,2009,29(12):1679-1688.
[责任编辑:关金山 英文编辑:刘彦哲]
Variable Structure Control for Uncertain Multi-Input Discrete-Time System
CHEN Xiu-qin1,ZHAO Na1,LI Jun-tao2
(1.School of Mathematics and Computer Science,Xinyang Vocational and Technical College,Xinyang,Henan 464000,China;2.College of Mathematics and Information Science,Henan Normal University,Xinxiang,Henan 453007,China)
Objective This paper proposes a design of a new variable structure controller against a class of multi-input discrete uncertain systems.Methods By using Lyapunov theory and variable structure control theory,it is analyzed that when the system parameters perturbation and external disturbances satisfy certain conditions,a new estimation for uncertainties is proposed with the method of designing observer.According to the estimator designed in this paper,the estimating error of uncertainty is less than standard.And when if uncertainties change slowly,the observation error is close to zero.Results According to the variable structure control theory,the system’s chattering is difficult to avoid.So how to deal with uncertainties is the key to reduce the chattering.The design of uncertainty estimator is used to solve the problem.The appropriately selected switching function and controller can make all states of the system fall into a certain area.Especially when the uncertainty change is slow,the closed-loop system is asymptotically stable,which can make the system chattering exponential decays to zero.Finally the simulation examples verify the effectiveness of the proposed method.Conclusion Sliding mode variable structure controller given in this paper can effectively reduce the chattering of the system and improve the performance of the system.
uncertain discrete-time system;sliding mode control;uncertainty estimator;chattering
国家自然科学基金(61203293);河南省重点科技攻关计划(122102210131)
陈秀琴(1981-),女,河南信阳人,信阳职业技术学院讲师,理学硕士。
O 415.5
A
10.3969/j.issn.1673-1492.2016.07.001

