新课改背景下高中数学小组合作教学模式的实践与探究

丁永信

（正宁一中）

新课改背景下高中数学小组合作教学模式的实践与探究

丁永信

（正宁一中）

新课改要求学生具有自主、合作学习意识及合作能力。在这种意识与能力的培养过程中，小组合作学习不失为一种兼顾学生学习能力与个性成长的有效教学模式。通过亲身的教学实践探索，以“函数的单调性”为教学案例，分析总结了小组合作学习对教师和学生的影响。

新课程改革；小组合作学习；高中数学；案例探究

一、小组合作学习模式的内涵

合作学习概念的界定应至少涉及以下几个层面：（1）合作学习是以小组活动为主要方式的学习活动；（2）合作学习是同伴之间互帮互助的学习活动；（3）合作学习是在强调小组的总成绩的同时也重视个体成绩的学习活动；（4）合作学习是以达成某种目标而全面展开的学习活动；（5）合作学习是在教师的指导下分配和指定学习任务学生主要参与完成的学习活动。

而根据新教改的要求，在教学过程中，教师应给学生提供充分的空间以展示自己的才能，让学生亲身感受学习过程中问题的提出、探究及解决途径，以达到掌握科学的研究学习方法的过程，在整个过程中全面培养学生的自主探究意识、合作创新意识，让学生感受学习的乐趣、成功的喜悦，进而提升学生的自主学习能力、问题处理能力以及合作学习能力，使学生形成正确的学习观和价值观。由此，小组合作学习的教学模式则被界定为：学生先根据教师提供的学案进行自觉、主动、独立的探究学习，在学习的过程中，标注出自己不懂的问题再与组内成员合作探讨、互帮互助寻求解决途径，最后在老师的点拨下得出正确结论并理解所学知识且达到熟练掌握运用的程度。

二、学习小组的建立

学习小组建立的原则：组间同质，组内异质。组间同质，是指组与组之间学生的综合素质基本相同，男女搭配基本平衡，便于在组间开展竞争。学生综合素质包含德、智、体、美等各个方面，具体指学生的纪律表现、行为习惯、学习总成绩、单科成绩、艺体特长等。组内异质，是指同一组内的学生具有层次性，学生的分布呈阶梯状，以利于传、帮、带，分散待优生，降低学习管理难度。

三、小组合作学习在“函数的单调性”教学中的实践探索

本案例以人教版高中数学教科书（必修）第一册（上）第二章第三节的内容“§2.3函数的单调性”为教学内容。函数的单调性是初中有关内容的深化和提高，为后面学习指数函数、对数函数及数列这些特殊的函数打下基础，与不等式、求函数的值域、最值、导数等都有着紧密的联系。因此，该教学环节在整个函数学习过程中起到至关重要、承上启下的作用，如何使学生准确把握函数的单调性的内涵，本节课在学生认识了函数的单调性概念基础上，让学生通过小组合作的学习方式，自己观察、探索研究获得函数单调性。

教师做出指令，要求学生分别作出函数y=x+1，y=-x+1，y=x2，y=（x≠0）的图象，小组合作讨论：观察自变量变化时，函数值有什么变化规律？

教师根据学生讨论的情况适时指导学习小组，八个小组中有六个小组的讨论初见成效，但是很明显有两个小组的学生茫然地作图，只有为数不多的几个学生在小声议论，教师根据学生的作图情况，选取了几个学生的作图投影，引导学生观察图象，由于第一和第二个图的变化规律比较简单，教师只请了一个组的代表发言。

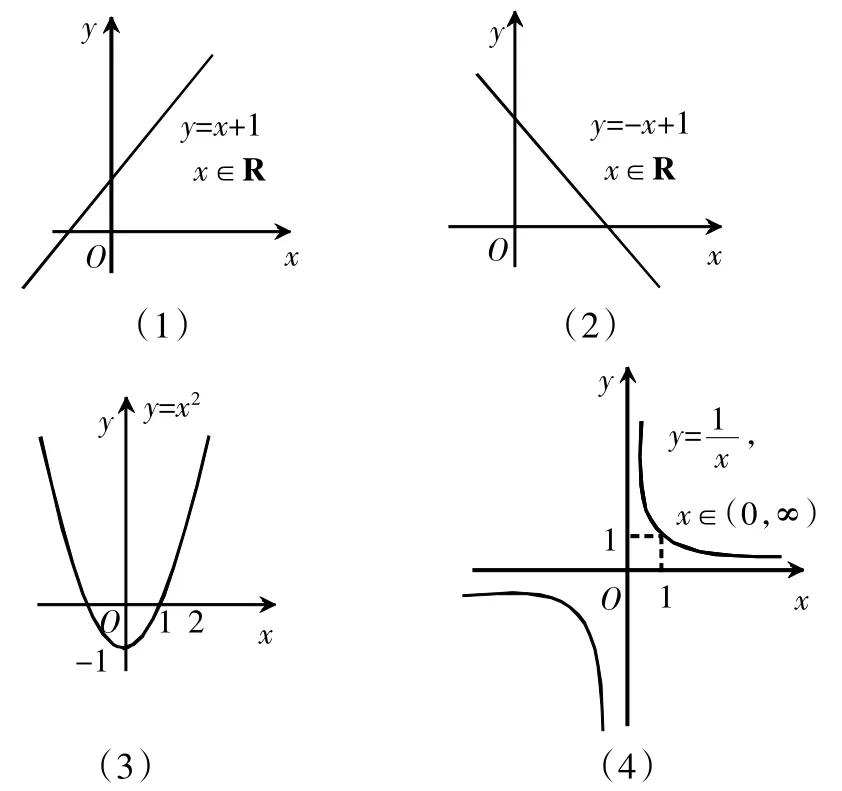
【小组1】从左往右上升，y随x的增大而增大；第二个图象从左往右下降，y随x的增大而减小。

【小组2】第三个图象函数y=x2在［0，+∞）上y随x的增大而增大，在（-∞，0）上y随x的增大而减小。

【小组3】第四个图象函数y=x2在（0，+∞）上y随x的增大而减小，在（-∞，0）上y随x的增大而减小。

......

而后，教师引导学生明确函数的局部性质，需要根据定义域的取值范围进行讨论。

第一、第二的函数图象较为简单，各个小组都能准确判断及理解单调性与图象的关联性。

对第三、第四个图象的讲解是难点，教师抽查了3个小组的部分学生回答，让学生组内讨论得出函数这两个性质是对定义域内固定区间而言的，此时函数的单调性是函数的局部性质，而后教师进行了补充讲解。

通过探索，培养了学生的观察能力和运动变化的观点，同时充分利用图形的直观性，渗透了数形结合的思想，学生在探索的过程中品尝到了自己劳作后的甘甜，感受到耕耘后的丰收喜悦，更激起了学生的探索创新意识。

总之，新课改的关键是教师和学生在教学活动中角色的转换，即学生成为学习的主人，处于主体地位，而教师则是学生学习的服务者和引导者，处于主导地位，小组合作式教学模式则可以充分地使师生在教学活动中发挥相应的作用，有利于学生的学习和发展。

徐东红.新课改背景下高中数学互动合作学习模式探析［J］.未来英才，2014（4）.

·编辑薄跃华