基于“关注思维,提升学力”的高中数学教学设计的探究
——由一堂公开课引发的教学设计优化探究
王燕萍
(浙江省桐庐中学)
基于“关注思维,提升学力”的高中数学教学设计的探究
——由一堂公开课引发的教学设计优化探究
王燕萍
(浙江省桐庐中学)
以一堂“方程的根与函数的零点”引发出教学设计优化,从课堂教学优化的实例分析着手,着重从巧设情境激活思维的启迪点,提升转化划归的学力;暴露问题激发思维的冲突点,提升自学阅读的学力;精选例题培养思维的着力点,提升学以致用的学力;探究实践构建思维的关联点,提升抽象概括的学力;活动多元攻克思维的突破点,提升辩证分析的学力等方面对教学设计优化进行探究。
教学设计;巧设情境;自主学习
一、巧设情境激活思维的启迪点,提升转化划归的学力
对引入的逐次优化:第1稿引入:从不同的视角看y=x-1,有什么样的理解?
第2稿引入:当李宗伟把羽毛球挑到后场后,羽毛球的高度随时间变化的函数关系式为:h=-t2+t+1,林丹若能在羽毛球落地前把球回过去,至多需要几秒?
第3稿引入:当李宗伟把羽毛球挑到后场后,羽毛球的高度随时间变化的函数关系式为:h=-t2+t+1,林丹若能在羽毛球落地前把球回过去,至多需要几秒?
在不冲淡教学重点的前提下引入这些学生感兴趣的题材能引发学生思维,有效激发学生的学习主动性和探究欲。这稿的引入,形式新颖,贴近生活。在上课之前我就用优酷播放了林丹和李宗伟的羽毛球比赛视频,有多方面的目的和好处,如下:
1.提前吸引了学生的注意力,在学生没有任何压迫感的情况下,不知不觉中提前进入课堂状态。巧设问题情境,即时激活学生思维,找到思维的启迪点,提升分析问题的学力。
2.通过这个实例中问题的设置让学生体会数学是来源于生活的,数学是有用的。在对学生的思维进行开发之际,要引导学生学会如何从数学角度探究生活问题。
3.在分析“林丹若能在羽毛球落地前把球回过去,至多需要几秒?”的过程中,转化为方程思想,接着又在分析方程的根的几何意义的过程中引出函数的零点概念,体现了函数的零点与方程的根之间的“动与静的结合”“整体与局部的转化”“函数与方程的思想”“特殊到一般的递进”,感受到数学学习的脉脉相关,自由转化的奇妙性和奇趣性。
二、暴露问题激发思维的冲突点,提升自学阅读的学力
对概念掌握的逐次优化:对于概念辨析时用到的两个小练习:
练1.判断(-1,0),(3,0)是否是函数y=x2-2x-3的零点?
练2.函数y=(fx)的图象如下,则其零点为

虽然我在3稿中都用的是这个练习,但是对怎么用这两个练习的设计是不同的。首先,用两个小练习的意图是很明显的,就是通过这两个练习的顺利完成达到从代数和几何两个角度去求函数零点的目的。但在前两次中,我是打算直接在课堂中用问答模式,然后师生共同纠错分析的方式进行。在正式上课的过程中,我将这两个练习设置到了预习作业,也就是在课堂前置作业中完成,这样就给课堂教学争取了更多的时间,另外也培养了学生自学概念的能力。将常见的错误类型直接在课堂中拍照呈现,然后让学生自己发现概念的准确表述,认识到自己在自学概念的过程中认识上产生的盲点,增强概念把握的准确性和印象的深刻性。很多学生在预习过后会顾名思义地误认为(-1,0),(3,0)是函数y=x2-2x-3的零点。让其中一个学生作为代表去回顾零点的概念,自己感悟出“零点是实数,零点不是点”的严格要求。让学生直面自己在阅读自学过程中的问题,自己参照课本找到思维冲突点,提升自学阅读的学力。这对以后学习直线的截距及函数的极值点等相类似的概念都会起到辅助作用。
三、精选例题培养思维的着力点,提升学以致用的学力
对例题设置的逐次优化:都是求函数的零点,第1稿的形式过于单薄,不能覆盖所有的题型,而且例题在难度上梯度不够,还不能提炼出求函数零点的主要解决方法。第2稿在呈现形式上就较第1稿丰满,但在知识和方法上有重复的嫌疑。第3稿则在前两稿的基础上进一步优化:
1.两个例题的选择有梯度,有连贯性,而且具有典型性,对能利用图象的,直接解方程求的,含参的,不能直接求的都有涉及,4个小题的搭配比较合理。例题分析,突破重点,培养各种类型求函数零点的思维着力点,提升把握概念、学以致用的学力。
2.例1的4个小题的解决过程中,达到进一步感悟从代数和几何两个等价转化角度理解函数的零点概念。第(3)小题又对高中阶段重要的二次函数的零点有了一个小结,培养了数形结合、分类讨论的思想。第(4)小题的设计达到引出零点存在定理的目的,通过观察、归纳、猜想自然过渡到下一环的教学过程情境中,使得课堂内容设置环环相扣,引人入胜。通过对例1(4)的变式,过渡到例2,实现解决对于不能精确求出函数零点的问题,可以通过“一分为二”和“从一而终”两个角度分析零点的个数以及判断零点所在的大致区间。
3.例2的多角度分析和探究,其中“一分为二”和“从一而终”都是从形的角度去分析,而“定理+单调性”就实现了数的角度探究,而且对其中一个教学重点即“零点存在性定理”在理论学习过后,例2的出现又恰好使“零点存在性定理”得到了应用,加深了印象,进一步在问题解决的过程中突破教学难点。鼓励一题多解,肯定了思维的多样性。
四、探究实践构建思维的关联点,提升抽象概括的学力
对本质揭示的逐次优化:在定理感知中3稿虽然都用了下面这个探究过程:如图①、②、③、④中分别有A,B两点,试用连续不断的一条或几条函数曲线(如用一次函数曲线,二次函数曲线等)将A,B两点连接,则连线一定会与x轴有交点的图是___。

图1

图2

图3

图4
但探究的形式作了优化处理,前2稿是引导学生作图,然后归纳判断,而第3稿则采用了“闭眼脑补”的形式。主要原因是在课堂实践的过程中,根据学生课堂实践的活动,发现学生其实认为这是一个很容易得出结果的问题,根据生活经验都可以得出正确的结论,这个地方让他们兴师动众,大张旗鼓地作图探究就显得有些形式化了。而且在后面的用计分类的过程,本身就需要通过作图去判断命题的真假,这里再作图就显得重复和多余了。而且在探究过程中去掉了一些影响判断的干扰条件,如只留下有需要的x轴,和A,B两点与x轴的位置关系,对提高分析问题的能力起到一定的作用。随后尝试着将这种直观感知、生活经验转化为数学的语言描述,大大促进了学生数学思维品质的培养,提高了数学素养,认识了如何用数学的观点去剖析和解决实际问题的过程和途径。将问题抽象概括为数学问题,构建出两点与x轴的位置关系,与函数值的同号或异号的思维关联点,提升抽象概括、直观感知数学的能力。
五、活动多元攻克思维的突破点,提升辩证分析的学力
1.教学中,始终体现学生为主体,教师为主导,学思结合的理念,循序诱导,最终让学生一点一点到达存在性定理。在定理感知过程中,通过例1(4)的探究实现了通过归纳猜想初步获取定理,通过“闭眼思过”的形式进一步肯定了定理,通过“将直观感知转化为数学语言”培养了抽象概括的能力。
2.在定理辨析过程中,用计分类,实质上是从“增加结论限制”“条件和结论互换”“减少条件”“条件和结论均否定”“小范围改大范围”“大范围改小范围”即命题与逻辑的多种角度对定理的条件和结论的关键点进行解读,增强定理理解的深刻性和定理把握的准确性。
3.在“变形计”各计正误的判断过程中,用计分类的过程中,再次对定理感知中分别位于x轴同侧和异侧的两点进行连接,不仅一环扣一环,而且在“巩固数形结合,反例推翻的方法应用的有效性来进行命题正误判断”过程中发挥了作用。
基于“关注思维,提升学力”的高中数学教学设计,重点可以以关注如下思维,提升如下学力为主:
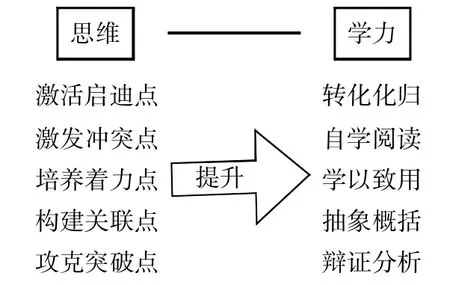
知识的获得与技能的形成,全靠思维运作;思维的运作又会让学生把知识掌握得更加透彻到位。在活跃的思维中,学生的学力自然就得到了提升。在这一次主题教研活动过程中,通过反思的行为改进有利于教师反思自我,形成困惑,成为下一次行动改进的起点。
钱健.探究式教学案例及反思[J].中学数学月刊,2012(5).
·编辑李建军

