多角度分析，“最”能解决二次函数难题

郑小雨

（福建省宁德市民族中学）

多角度分析，“最”能解决二次函数难题

郑小雨

（福建省宁德市民族中学）

二次函数是初中数学学习的重点与难点，是各类考卷中的必考题型。身为教师，通过思路清晰、综合有效的教学使学生掌握这部分知识内容是教师的重要使命。根据多年的教学经验，浅谈几点有效解决二次函数求最值问题，提高学生学习效果的教学策略，具有一定的参考意义。

初中数学；二次函数；多角度；区间

二次函数求最值类的问题千变万化，然而只要掌握一定的技巧，学会多角度分析，定能找到解题思路，以不变应万变，顺利解决难题。本文以二次函数求最值问题的题型为基础，进行了解题模式的探讨。

一、确定区间，结合图象性质

数形结合是解决数学问题的有力武器，在解决二次函数求最值的问题中也不例外，通过结合图象性质，快速准确地确定区间，开辟出解题思路。

1.定轴定区间，直接判断

当二次函数所给的函数区间固定，对称轴固定时，我们可以通过做出函数图形，清晰直观地判断和计算出函数的最值。这类题型比较简单，所以我在教学中，主要教会大家准确地做出函数图形，从而解决问题。

比如，对于定轴定区间函数求最值问题：求函数y=-x2+4x-3在区间［1，4］的最大值及最小值。首先我们分析二次函数的表达式，二次项系数小于零，说明函数图象开口向下，函数的对称轴为x==2。然后我们根据区间范围，函数的对称轴，开口方向可以做出该二次函数的草图。通过观察这一函数的图象，我们可以得出二次函数的最大值应在对称轴处取得，二次函数的最小值在端点x=4处取得，通过将x轴的坐标轴代入函数表达式，即可求出相应的最大值与最小值，从而得解。

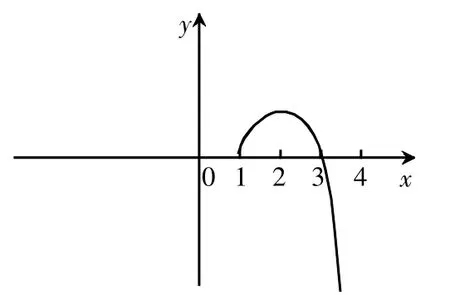
图1

2.定轴动区间，相对位置

定轴动区间类的二次函数其对称轴确定，然而闭区间是不确定的。这类问题考查的是对称轴与函数区间的相对位置关系，当函数区间发生变化时，随着与对称轴的相对位置发生变化，函数的最值也可能会发生变化，所以学生要掌握分类讨论的思想，讨论不同情况下的函数最值。

例如，求函数y=x2+2x-1在区间［t，t+2］上的最大值与最小值。这道题的类型属于定轴动区间类问题，首先我们确定函数的对称轴为x=-1。随着t的取值不同，我们发现可以将这一问题分为三种情况进行讨论，一是当对称轴位于区间［t，t+2］的函数右侧时，二是当对称轴位于区间［t，t+2］的函数内时，三是当对称轴位于区间［t，t+2］的函数的左侧时，进而可以将t的值也划分为三个范围进行讨论。在第一种情况下，t+2＜-1，t＜-3，通过观察二次函数y= x2+2x-1在［-∞，+∞］上的图象可以发现，位于对称轴左侧的函数图象是单调递减的，因此t＜-3时，函数在x=t处取得最大值，为t2+2t-1，在x=t+2处取得最小值，为（t+2）2+2（t+2）-1。在第二种情况下，-3≤t≤-1，由于对称轴在区间范围内，对称轴处函数取得最小值，为-2。然后通过比较函数区间端点与对称轴的距离大小可以取得函数的最大值，因此第二种情况进而再分两小类问题讨论，当-3≤t＜-2时，函数最大值在x=t处取得，为t2+2t-1，当-2≤t≤-3时，函数最大值在x=t+2处取得，为（t+2）2+2（t+2）-1。在第三种情况下，同样观察如图2所示图象，我们能够发现区间范围内的函数图象在对称轴右侧时，函数是单调递增的。因此，t＞-3时，二次函数在x=t处取得最小值t2+2t-1，为在x=t+2处取得最大值（t+2）2+2（t+2）-1。

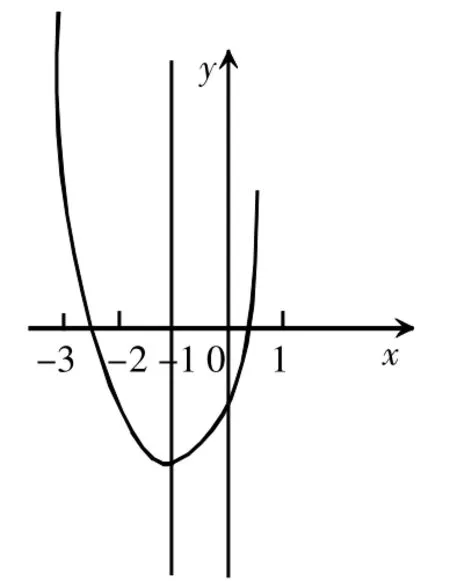
图2

讲完例题后我向学生强调了这类题型的易错点。定轴定区间类的二次函数求最值问题相对来说是最简单的求最值问题，然而学生因为粗心大意也会发生错误，比如画错开口方向，大家一定要记住二次项系数大于零开口向上，二次项系数小于零开口向下。然后端点处和对称轴处的函数值只要将对应的x值代入函数表达式，便可准确地求出，进而做出函数图象。

在这部分知识的教学中，我通过强调做函数图象的细节，引导学生在做题时通过直接地观察，准确地得到最值，提高了课堂的效率。

在上述例题的教学中，我通过引导学生进行分类讨论，将问题分为各种情况然后求出最值，思路清晰，条理明确，能够完整准确地确定该类二次函数的最值，取得了很好的教学效果。

3.定区间动轴，考虑变量

对于定区间动轴类的二次函数问题，由于区间固定而对称轴不确定，因此函数的最值也会随着对称轴与区间的相对位置变化而发生变化，因此解决这类问题同样需要进行分类讨论，与定轴动区间类最值问题相似。

例如，求二次函数y=x2-ax+1在区间［0，2］上的最小值。我引导学生依照定轴动区间问题的求解思路，将该问题分成三种情况进行讨论。通过计算，可得到二次函数对称轴为x=a，当区间范2

围内的函数位于对称轴左侧时，即a＞4时，函数在区间［0，2］内是单调递减的，因此二次函数在x=2处取得最小值，为5-2a。当对称轴包含在区间范围内的函数时，即0≤a≤4，由于该二次函数开口向上，所以在对称轴处取得最小值，为a2-a2+1。分析到这一步的42时候我向学生强调了求最大值的做法，这道题仅让求最小值，而恰好对称轴处为最小值，若这道题还要求求出最大值的话，学生也应按照定轴动区间类问题中这种情况下的解题思路再次进行分类讨论。当区间范围内的函数位于对称轴右侧时，即a＞0时，函数在区间［0，2］内是单调递增的，因此，二次函数在x=0处求得最小值1。

图3

在上述问题的教学中，我通过引导学生利用定轴动区间类最值问题的求解技巧与思路，顺利地探求出动轴定区间类问题的求解方法，通过这样类比与分类的讨论思想，让学生成功地理解与学会了这部分数学知识，高效地完成了教学目标。

二次函数的对称轴位置、函数区间都会对二次函数的最值造成影响，学生在解题时，一定要看清题目对对称轴和区间的要求，多角度分析问题，采取正确的解题策略。

二、含有系数，字母视为常数

有时求最值问题所给的二次函数的系数是用字母表示的，对于这类问题的求解方法是将字母视为常数，并根据字母所表示的系数的位置不同，可能需要进行分类讨论。

二次函数的表达式可写作y=ax2+bx+c，当所给函数的常数项用字母表示时，自然将其视为常数处理。例如，求二次函数y=x2+ 2x+a在区间［0，1］上的最大值。二次函数在［0，1］上单调递增，x=1时函数的最大值为3+a。当所给函数的一次项系数用字母表示时，这类问题就是上述所讲的动轴定区间类问题，将字母视为常数，再结合自变量的范围，按照分类讨论的思想进行求解。当所给函数的二次项系数用字母表示时，例如，求二次函数y=ax2+4x-3（a≠0）在区间［1，3］内的最大值。对这一例题进行分析，a的大小首先影响的是开口大小，因此首先分为a＞0和a＜0这两大类进行讨论。当a＜0时，对称轴x=-4/2a＞0，转化为动轴定区间问题。当0＜-2/a＜1即-2＜a＜0时，二次函数在［1，3］内单调递减，x=1时取得函数最大值为a+1；当1≤-2/a≤3即-2/3≤a≤-2时，函数在对称轴处取得最大值，为-4/a-3；当-2/a＞3即a＜-2/3时，函数在［1，3］内单调递增，x=3处求得最大值为9a+9。当a＞0时，对称轴x=-＜0，函数在［1，3］内单调递增，最大值在x=3处取得，为9a+9，从而得出了变量a在不同取值范围内二次函数的最大值情况。

在上述教学中，我通过教授学生将含有字母的系数视为常数的思想，引导学生攻克了含有参数的二次函数求最值问题，加深了学生对二次函数的理解与运用。

三、实际应用，正确列函数式

二次函数在实际生产生活中也有很广泛的应用，通过利用二次函数求最值的方法，我们能够解决最优化问题。对于二次函数在日常生活中的应用问题进行分析，正确列出函数表达式是非常关键的步骤。

例如，某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台。为了响应国家“家电下乡”政策，商场决定降价。冰箱售价每降低50元，平均每天能多售出4台。那么每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润为多少？求解这道题，我们首先应当确定冰箱的利润y与每台冰箱降价x的函数表达式，y=（2400-x-2000）（×4+8）=-x2+24x+ 3200。我们可以做出该函数的图象，对称轴为x=150。

然后结合自变量x的取值范围，我们可以求得二次函数在对称轴处取得最大值，也就是说，当冰箱降价150元时，商场的利润最大为5000元。然后我对二次函数应用题进行了总结，这类问题学生首先应该读清题意，确定正确的函数表达式，然后应用定轴定区间二次函数求最值的求解方法，即可求得应用题中的最优结果。

图4

在上述教学中，我对如何将实际生活问题转化为数学二次函数极值问题的处理方法进行了讲解，引导学生学会有效地结合函数图象进行解题，应用二次函数的性质，成功地求解出应用题的正确答案，进一步加深了学生对二次函数知识的掌握。

多角度分析是促进思维、加快解题速度的一种好方法。综上所述，学生只要切实掌握确定函数区间的技巧，把握住含有系数的二次函数与二次函数的实际应用解法，就能成功地克服部分二次函数难题。总之，从多角度分析和解决问题，有助于迅速找到解题思路，提高学生的数学素养。

［1］徐薇.浅谈初中数学二次函数最值问题的求解［J］.数理化解题研究：初中版，2015（13）：26.

［2］许艳.二次函数中最值问题的求解［J］.中学生数学，2015（6）：13-14.

［3］杨寒英.二次函数最值问题及其解决方法［J］.中学教学参考，2014（32）：50.

·编辑李建军