质疑式数学概念教学的策略研究
(作者单位:山东大学附属中学,山东济南 250000)
◎学科教学◎
质疑式数学概念教学的策略研究
■王道远
数学概念是揭示现实世界空间形式与数量关系本质特征属性的思维形式,也是数学基础知识和基本技能的核心。其根本任务是准确地理解数学概念的内涵和外延,使思考问题、推理证明有所依据,能有创见地解决问题。因而,数学概念课的教学尤为重要。
一、理论介绍
基于传统教育学、心理学理论,概念教学主要有概念的形成和内化两种方式。
概念的形成一般是针对由弱抽象形成的概念。如果某些数学对象的关键属性主要是在对大量同类数学对象的不同例证进行分析、类比、猜测、联想、归纳等活动的基础上,独立概括出来的,那么这种概念获得的方式就叫做概念形成。这一过程主要涉及以下相关因素:①感知、辨别各种刺激模式。②抽象出各刺激模式的共同属性,并提出假设。③在特定的情境中修正、检验假设,形成概念。④把新概念一般化,并用数学的语言符号表达。
概念的同化一般是针对由强抽象形成的概念。如果学习过程是已定义的方式直接向学生呈现概念的关键特征,实际上是新的数学概念在已有概念的基础添加其他新的特征性质而形成。这时,学生利用自己的认知结构中已有的相关知识对概念进行加工、改造,从而理解新概念的意义。这种获得概念的方式叫做概念同化。
这两种方式偏重于概念的逻辑结构教学忽视数学概念本身的涵义,数学概念具有“过程”——“对象”的双重性,概念教学既是逻辑分析的对象又是具有现实背景和丰富寓意的教学过程,近些年新兴起了APOS理论,让学生从概念的现实原型、概念的抽象过程、数学思想的指导作用、形式表述和符号化的运用等多方位理解一个数学概念,使之符合学生主动建构的教育原理。关于APOS理论,杜宾斯基认为,学生学习数学概念是要进行心理建构的这一建构过程,要经历以下的4个阶段:第一阶段:操作阶段,第二阶段:过程阶段,第三阶段:对象阶段,第四阶段:概型阶段。从数学学习心理学角度分析,以上4个学习层次分析合理地反映了学生学习数学概念过程中真实的思维活动。其中的“活动阶段”是学生理解概念的一个必要条件,通过活动让学生亲身体验,感受概念的直观背景和概念间的关系;“过程阶段”是学生对活动进行思考,经历思维的内化、压缩过程,学生在头脑中对活动进行描述和反思抽象出概念所特有的性质;“对象阶段”是通过前面的抽象,认识到了概念本质,对其赋予形式化的定义及符号,使其达到精致化,成为一个具体的对象,在以后的学习中以此为对象去进行新的活动;“概型阶段”的形成要经过长期的学习活动来完善,起初的概型包含反映概念的特例、抽象过程、定义及符号,经过学习建立起与其他概念、规则、图形等的联系,在头脑中形成综合的心理图式。APOS理论揭示了数学概念念学习的本质是具有学科特色的学习理论。
二、流程设计
将APOS理论应用于传统的教育心理学中有关概念的原理,结合山东大学附属中学的实际学情、数学质疑式教学以及翻转课堂的教学研究,我们针对不同的概念形成了两种比较具有代表性的课堂流程:
(一)基于APOS理论的质疑式概念形成的教学环节设计

概念形成的教学模式需要对具体的,直接的感性材料进行观察、感知、操作等活动,比较耗时,一般适合概念体系中起着基础和核心作用的少数抽象概念的学习,如函数、分式的概念。
(二)基于APOS理论的质疑式概念同化的教学环节设计
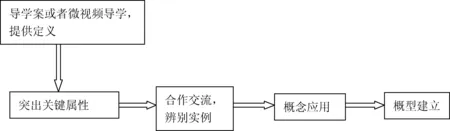
概念同化在课堂上直接给出定义,板书到黑板上或者课件上,由师生共同分析概念的内涵,把握概念的本质属性,结合预习提出的问题,进一步辨别概念的外延,去伪存真,把握概念。适合不易归纳总结的抽象性比较强的概念,如单项式、多项式、同类项等概念的学习。
APOS理论强调把数学概念寓于现实社会背景中,学生通过活动亲身经历、体验数学与现实的联系,从中经历完整的学习过程,用数学的方法组织和建立数学概念,这样建立起来的概念具有丰富的内涵,其中包含着概念的现实原型、概念的抽象过程、数学思想方法和概念的形式化对象等,如代数式、轴对称现象。通过APOS理论对于传统教学的优化,更加注重概念的建构过程,在学习过程中重现了概念探索的完整过程。
三、案例分析
北师大版八年级(上)第四章《函数》
(一)教学目标
1.知识技能目标:(1)学生通过直观感知,领悟函数概念的意义,能列举生活中的函数实例;(2)学生通过对实际问题中数量之间相互依存的关系的探索,学会用函数思想去进行描述,初步理解对应。
2.过程与方法目标:(1)通过实践与探索,学生参与函数概念的形成过程,领悟数学的应用和初步函数模型,提高分析问题和解决问题的能力;(2)引导学生体会函数思想,逐步形成较好的思维品质。
3.情感目标:(1)学生经历对实际问题数量关系的分析探究,学会合作学习。
(二)重、难点
1.重点:函数概念的形成过程。
2.难点:理解函数概念,突破难点的关键是通过实例帮助学生从函数的本质进行引导理解。
(三)教学过程

第一环节:引入。
世界万物都是在不停地运动变化的,这些运动变化都有一定的规律,如何来研究这些运动变化并寻找变化规律呢?数学上常常用函数来刻画各种运动变化,从今天开始,我们将通过实际问题进入函数的世界,一起领略函数及其图象的美。
第二环节:合作交流,聚焦问题。
给出讨论的问题:
1.在三个实例中,确定自变量、因变量分别是什么?
2.因变量随自变量如何变化?
3.对于自变量的每一个值,有没有因变量的值和它对应,值有几个?
4.在三个实例中,共同点是什么?
第三环节:结合问题,质疑提升。
预设学生的问题:
1.自变量的取值范围是什么?
2.怎样算自变量的取值范围?
3.所有函数都能用图像表示出来吗?
4.函数有何分类?
5.我们可以直接在图像中看出是否为函数吗?其他形式呢?
6.是函数式数吗?是什么?怎样表示两个变量的函数关系?如何快速判断是否函数?无规律的变量变化是函数吗?怎么表示?
结合学生提出的问题及导学案中给出的实例,进一步深化学生对于函数的理解。经过师生的共同讨论,总结出三个实例的共同点就是:有一个变化过程,都有两个变量,给定其中某一个变量的值,相应地就确定了两一个变量的值,这个值并且是唯一的。(学生可能回答不到位,注意引导)。
第四环节:抽象共性,形成概念。
我们把具有这些共同特征的对应关系称为函数。
函数的概念:一般地,在某个变化过程中,有两个变量x和y,如果对于任意一个x的值,就相应地确定了唯一的y值,就称y是x的函数,其中,x是自变量,y是因变量。
概念的内涵:函数概念中的“任意一个”“唯一”,你是怎么理解的?理解函数的概念把握三点:一个变化过程,两个变量,对于自变量的每一个值,因变量都有唯一的值与它相对应即一种对应关系。判断两个量是否具有函数关系也应以这三点为依据,主要是第三点。
概念的外延:通过分析三个实例,可以把握函数的三种表示方式:图像、表格、关系式渗透数学史的知识:函数这个词是1895年李善兰首先翻译过来的,“函”是随……而变化的事物,强调了变化,两个变量之间的依存关系。
显然,在实际生活中,自变量的取值必须有意义,符合实际情况,在纯粹数学问题中,自变量的取值应该是让数学式子有意义。有关自变量的取值范围问题,我们将在陆续的学习中学到。
总之,中学的数学概念教学在数学教学中处于核心地位。教师要围绕这核心展开教学,在概念的理解和数学思维方式上给予讨论、质疑、训练,让学生在理解概念(理解其中的数学思想和方法)的基础上对细节问题、变化问题深入思考。并且,我们知道一个数学概念由“过程”到“对象”的建立有时是比较漫长的。如函数概念“过程”到“对象”的抽象需要经过多次反复,螺旋上升,直到学生在头脑中建立起数学知识的直观结构。教师在今后的教学中要注意学生对知识的概型建立,即加强知识间的联系和应用,帮助学生在头脑中建立起完整的数学概念的心理图示。
(作者单位:山东大学附属中学,山东济南250000)
(责任编辑:甄鸿启)

