数学教学回归教材的探究与反刍*
●岳 峻 韩长峰
(太和中学 安徽阜阳 236600)
数学教学回归教材的探究与反刍*
●岳峻韩长峰
(太和中学安徽阜阳236600)
教材是数学知识和思想方法的重要载体.教师的教学引领应立足于教材,强化回归教材的意识,掌握回归教材的方法,提升回归教材的引领技能,注重提升学生数学学科的核心素养.
数学教学;回归教材;探究;反刍;核心素养
数学教育专家总是反复强调必须追根溯源、回归教材,但一线教师对回归教材的理解有一定的偏差,误认为是所学知识的一味重复或机械相加,没有太大的意义,或者无暇投入,因此只是口头上重视回归教材,行动上难以落实,陷于疲惫的题海战,也有悖于《数学课程标准》的理念.
教材是编者集体智慧的结晶,是数学知识和数学思想方法的重要载体[1],又是教师的“教”和学生的“学”的主要资源,承载着新课程改革的理念和导向,渗透着创新精神和实践能力的培养,同时体现着高考改革的发展趋向.教材的结构是反复考量的,语言是字斟句酌的,例题是千锤百炼的,习题是精挑细选的,教材中每个素材的选取、问题的设置、规律的呈现等都具有极高价值.这就要求数学教学的根基必须在教材,切实落实“回归教材”.
笔者以2016年1月参加的联考阶段性测试试题为例,谈谈回归教材的探究与反思,供大家指正.
1 试题呈现,思路简析
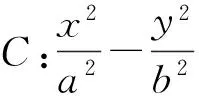
()
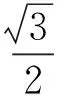

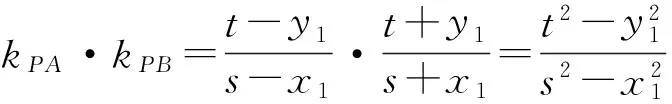
又因为点P,A∈C,所以
b2s2-a2t2=a2b2,b2x21-a2y21=a2b2,
2个式子相减可得
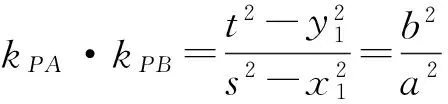

2 回归教材,追根溯源
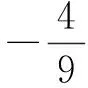
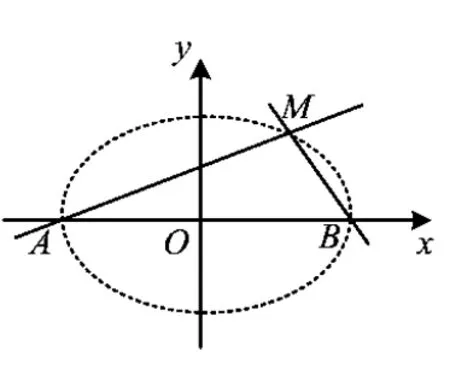
图1

图2

例4已知△ABC的2个顶点A,B的坐标分别为(-5,0),(5,0),且AC,BC所在直线的斜率之积为m(其中m≠0),试探求顶点C的轨迹.
例5设A,B的坐标分别为(-1,0),(1,0),直线AM,BM相交于点M,且直线AM的斜率与直线BM的斜率之商为2,问:点M的轨迹是什么?为什么?
例6已知点A,B的坐标分别为(-1,0),(1,0),直线AB,BM相交于点M,且直线AM的斜率与直线BM的斜率之差是2,求点M的轨迹方程.
例7已知点A,B的坐标分别为(-1,0),(1,0),直线AM,BM相交于点M,且它们的斜率之和是2,求点M的轨迹方程.
3 探究之旅,变式引申
3.1归纳拓展——定点字母化
我们不妨先探究其中一种情形,另一种可以由类比得到.通过简单的探究即可得知:
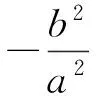

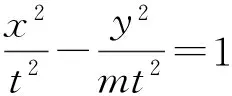
若m=-1时,点M的轨迹方程是x2+y2=t2(其中|x|≠1),显然也符合上式,因此变式3不仅包含了变式1和变式2,还包含了椭圆的极限曲线——圆.
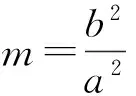
变式4设A,B的坐标分别为(0,-t),(0,t)(其中t>0),直线AM,BM相交于点M,且它们的斜率之积为m(其中m≠0),则点M的轨迹方程是

这自然得到有心圆锥曲线的第三定义:平面内的动点与2个定点的直线斜率之积等于非零常数m(其中m≠0)的点的轨迹为有心圆锥曲线.
3.2初步探究——命题逆化
上述变式的逆命题是否成立呢?亦即已知曲线方程和曲线上异于顶点的动点与相对2个顶点连线的斜率乘积会有什么结论呢?



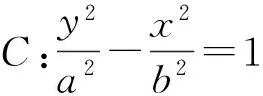
3.3深入探究——定弦运动化
变式5~变式8中弦AB的中点是原点O,且端点落在坐标轴上,试想:若弦AB的中点是原点O,但端点不落在坐标轴上,则结果又如何?



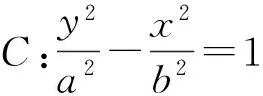
3.4意犹未尽——运算推广
教材上的后3题是将直线AM,BM的斜率之积分别调整为斜率之商、斜率之差、斜率之和,那么点M的轨迹方程又将会是什么呢?
变式13已知平面内的定点A,B的坐标分别为(-a,0),(a,0)(其中a>0),直线AM,BM相交于点M,且它们的斜率之商是m(其中m≠0),则点M的轨迹方程为
(1-m)x=±a(m+1)(其中|x|≠a).
变式14已知平面内的定点A,B的坐标分别为(-a,0),(a,0)(其中a>0),直线AM,BM相交于点M,且它们的斜率之差是m(其中m≠0),则点M的轨迹方程为
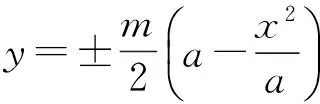
变式15已知平面内的定点A,B的坐标分别为(-a,0),(a,0)(其中a>0),直线AM,BM相交于点M,且它们的斜率之和是m(其中m≠0),则点M的轨迹方程为

显然当m=0时,变式14和变式15中点M的轨迹方程分别为直线y=0,x=0.
4 回归教材的反思
4.1强化回归教材的意识
回归教材,力促教材例习题的引领活力,展现习题功能,挖掘习题潜能.高考数学试题具有“源于教材,而高于教材;题在书外,但根在教材”的特点.年年岁岁题相似,岁岁年年意不同,万变不离其宗,其中的“宗”就是教材.教材中的题目大多都蕴含着深刻的背景、丰富的数学文化、数学思想,很多高考试题都源自教材中的定理或定理中的思想方法,或是例题、习题的重新整合、挖掘、引申等.有的高考题直接从教材的例、习题移植而来;有的高考题用教材的例、习题改编而来;有的高考题从教材的例、习题类比深化而来,即便是综合题也是教材例题、习题的组合、加工、引申、拓展和类比,充分体现教材乃高考数学试题之根之所在[2].
正如罗增儒语:教材是课程的载体,因此高考命题最具体、最方便的依据其实是教材.教材是中、低档试题的直接来源;教材是考试内容的具体化;教材是高考命题的基本依据;教材是解题能力的基本生长点.
因此,教师的教学引领应立足于教材,对教材中有潜在本质规律的例题、习题进行适当地挖掘、类比,使教材中的每一个例题、习题的作用发挥极致,从学生认识规律角度,由浅及深,展开变式,引领学生在其思维水平的“最近发展区”递进式地探索,逐步提升学生的数学思维素养.这就是数学教学的核心之所在.
4.2掌握回归教材的方法
1)注重教材定理、公式的推导过程.
当前,不讲基础而一味钻难题的做法是不可取的.2010年四川省数学高考试题中出现cos(α+β),sin(α+β)的推导,2011年陕西省数学高考试题出现了叙述并证明余弦定理,2013年陕西省数学高考文科试题出现等差数列前n项和Sn的公式推导,理科数学出现等比数列前n项和Sn的公式推导……
数学是一种科学的思维方法,要学会思考;数学也是一种操作活动,要熟练技能;数学还是一种问题解决的方法,要学会解题.高三数学教学不能简单地理解为学生熟记公式、定理和结论,然后进行题海训练,而应注重定理、公式的推导过程,培养良好的解题习惯、发展分析和解决问题的能力,领悟思维的诱导、调整、进阶、完善,领悟其蕴含的丰富的数学文化、数学方法、数学思想,重新全面梳理知识、方法,促使学生有层次地、递进地理解数学本质,从而提升学生的数学思维素养.
2)注重教材例题、习题的变式训练.
教材例题、习题看似平淡无奇,其实是呈现简洁、极富韵味的好题,值得细细品味.高三复习教学应诱导学生把特殊问题纳入更一般的范围,从特殊推广到一般,揭示事物的普遍规律,促使学生从会解一道题到会解一类题,由低层次到高层次,把数学思维提高到由例及类的层次,加速数学思维的优化.例如,人教版《全日制普通高中教科书(选修2-1)数学》第73页的第6题:
例8直线y=x-2与抛物线y2=2x相交于点A,B,求证:OA⊥OB.
分析其已知条件:①直线l:y=x-2是一条定直线,其斜率为1,在x轴上的截距为2;②抛物线C:y2=2x的特征量2p=2,而直线l所过的定点M(2,0)的横坐标恰好为2,是巧合还是有规律可循?
拓展思路1直线“活”起来[3]
①直线l的斜率不变,在x轴上的截距变为1,结论还成立吗?(不成立.)
②直线l的斜率变为3,在x轴上的截距不变,结论还成立吗?(成立.)
③直线l的斜率变为-1,在x轴上的截距不变,结论还成立吗?(成立.)
④直线l的斜率变为k,在x轴上的截距不变,结论还成立吗?(成立.)
⑤直线l的斜率不存在,在x轴上的截距不变,结论还成立吗?(成立.)
……
拓展思路2曲线“动”起来
①抛物线C变为C:y2=3x,其他条件不变,结论还成立吗?(不成立.)
②抛物线C变为C:y2=-2x,其他条件不变,结论还成立吗?(不成立.)
③抛物线C变为C:x2=-2y,其他条件不变,结论还成立吗?(不成立.)
④抛物线C变为C:x2=2y,其他条件不变,结论还成立吗?(不成立.)
……
拓展思路3条件共“舞”
①直线l的斜率变为k,在x轴上的截距不变,抛物线C变为:y2=2px(其中p>0),结论何时成立?(提示:2p=2.)
②直线l的斜率变为k,在x轴上的截距变为4,抛物线C变为:y2=2px(其中p>0),结论何时成立?(提示:2p=4.)
③直线l的斜率变为k,在x轴上的截距变为2p,抛物线C变为:y2=2px(其中p>0),结论成立吗?(成立.)
……
拓展思路4逆化命题
①直线l与抛物线C:y2=2px(其中p>0)相交于点A,B,若OA⊥OB,则直线l有何特征?
②直线l与抛物线C:y2=2px(其中p>0)相交于异于顶点的2个动点A,B.若OA⊥OB,则直线必过定点吗?
……
拓展思路5披上“神秘”外纱
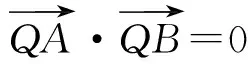
拓展思路6类比引申
①原点O是抛物线C的顶点,原点O变为抛物线C任意一点,是否还有类似的结论呢?
②抛物线C变为圆锥曲线中的椭圆、双曲线,是否还有类似的结论呢?
③抛物线C变为圆,结论是否成立?
……
3)注重教材阅读、探究的思维启示.
新课标教材充实了许多具有生活气息的阅读材料,吸引了学生的注意力,关注了学生的非智力因素对学习的影响,倡导学生的认知与兴趣、情感紧密地联系起来,实现情知并行、情知互动、情知交融,也设置了饶有情趣的探究问题,激发了学生学习的激情,促使学生产生探究的原动力和内在需求.
高三数学的复习教学,应对本原性的问题多一些思考,结合教材提供的阅读材料、探究问题的思维启示,创设开放、互动、新型的教学体验环境,促使学生体会知识的发生和发现过程,引领学生学会审题,学会思维,把教材中“省略”的思维信息慢节拍地找寻出来,提升数学探究教学的高效.
4)注重教材方法、思想的潜移默化.
形式化是数学的基本特征之一.在数学教学中,学习形式化的表达是一项基本要求.但是不能只限于形式化的表达,要强调对数学本质的认识,否则会将生动活泼的数学思维活动淹没在形式化的海洋里.新课程为了促进学生对数学内容本质的理解,建立内容本质与形式表达之间的有机联系,使数学形式化过程适应学生的学习心理,并在建构数学形式化认知结构的同时,获得全面发展,在“强调本质,注意适度形式化”方面作出了努力.
高中数学复习应返璞归真,努力揭示数学概念、法则、结论的发展过程和本质,注重教材方法、思想的潜移默化.数学教学要讲逻辑推理,更要讲道理,通过典型例子的分析和学生自主探索活动,使学生理解数学概念、结论逐步形成的过程,体会蕴涵在其中的数学方法、数学思想潜移默化,把数学的学术形态转化为学生易于接受的教育形态.
4.3提升回归教材的引领技能
凸显数学本质,引领学生思维,既是高中数学新课程的核心理念之一,也是数学学科的自身诉求.数学教学的一个重要任务就是抓住基础,抓住数学的核心,培养学生的数学思维素养,进而才能提高学生分析问题、解决问题的能力,提高学生的转化与化归的能力,才能化无限为有限,才能多题归一[4].
“做题不在多,理解则灵;难度不在大,有意才行”,教学时,教师要有意识地选准具有示范性、发散性、延伸性的试题,加以引申、拓宽、变化,引导学生从形式的“变”发现本质的“不变”,从本质的“不变”探索形式的“变”的规律,旁通知识的横向联系,注意知识结构的重组与概括,揭示其内在的联系与规律,精学一题、妙解一类,固化于型、内化于心,进而形成一个条理化、有序化、网络化的高效的有机认知结构,从中提炼出数学思想、数学方法.这就是数学教学的核心.
5 结束语
作为教师,务必将教材视为高三复习的“红色根据地”,在领会教材的编写特点、把握教材、理解教材、理清知识发生发展的来龙去脉的基础上,着力揣摩教材的编写意图,明确教材的脉络结构,深刻领悟数学知识的作用和蕴含的人文素养的文化价值,做到跳出教材、活用教材,提升自身的教学品味.也只有让学生时刻把“举一反三”“触类旁通”放在心上,经常实践,学会独立思考,才能提升学生数学学科的核心素养.
正如章建跃博士语:高考复习,回归教材、回归基础才是正道.急功近利的高考复习可以休矣!
[1]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003.
[2]岳峻.提升数学思维素养的教学实践与反思[J].中学数学,2015(12):94-96.
[3]岳峻,阮艳艳.细品圆锥曲线与直线一例[J].数理天地,2016(2):4-5.
[4]岳峻.透析考题信息提升解题驱动力——赏析2015年湖北卷第21题[J].中学教研(数学),2015(8):30-32.
�2016-04-25;
2016-06-01
岳峻(1968-),男,安徽阜阳人,中学高级教师.研究方向:数学教育.
O123.1
A
1003-6407(2016)10-01-05

