基于散射参数法的EMI滤波器电磁噪声抑制效果预测
王世山 龚 敏 宋 峥
基于散射参数法的EMI滤波器电磁噪声抑制效果预测
王世山 龚 敏 宋 峥
(江苏省新能源发电与电能变换重点实验室(南京航空航天大学) 南京 210016)
EMI滤波器是抑制传导噪声的重要手段之一,尤其是高性能的EMI滤波器的应用,对电力电子设备的干扰具有很好的抑制作用。基于传输线理论得到并联传输线的共模及差模参数,通过推导和测试得到噪声源阻抗、负载阻抗及其等效结构,求解得到基于阻抗法的插入损耗(IL)。但是,在高频条件下,EMI滤波器及传输线不仅存在自寄生参数,还存在互寄生参数,这些互寄生参数很难通过阻抗法来等效。本文在传输线等效共模与差模参数频率特性的基础上,根据传输线理论得到噪声源阻抗及负载阻抗;以共模滤波器为例,基于阻抗法预测滤波器对噪声的衰减能力,并与实际测试值进行比较。然而,由于阻抗法不能很好地预测高频条件下的噪声衰减,本文以波的“入射与反射”为核心,进一步提出一种利用S参数来预测阻抗不匹配条件下噪声衰减的方法,研究表明,散射参数法由于考虑了元件间的互寄生参数,具有更好的高频性能。
EMI滤波器 差模噪声 共模噪声 阻抗不匹配 S参数
0 引言
根据国际电磁兼容标准,所有的电力系统及电力电子设备的电磁干扰均需在所选标准线以下。在150kHz~30MHz间主要是传导干扰为主,而电磁干扰(Electromagnetic Interference, EMI)滤波器是抑制传导干扰的主要手段之一[1],因此,设计合适的滤波器不仅有利于抑制噪声,使其满足抑制标准,还有利于减小滤波器的体积,防止过设计[2]。
迄今为止,EMI滤波器的设计方法主要有以下几种:一种是假设源、负载阻抗均为50W,阻抗匹配条件下对EMI滤波器各参数值进行设计[3];另一种是假设噪声源阻抗与频率呈函数关系,而负载阻抗为LISN端恒定阻抗,通过测试噪声源阻抗的最大值及最小值实现最坏条件下的EMI滤波器设计[4]或最坏情况下的设计[5]。
然而,受测试要求及环境条件的影响,EMI滤波器与LISN及待测实物间均存在功率传输线,噪声测试电路如图1所示,这些功率传输线使得噪声的源、负载阻抗值并不是保持特定值不变[6,7],而是随着频率的变化而变化。且处于高频段时,衰减特性受到寄生参数的影响[8,9]。因此预测实际测试电路中EMI滤波器对噪声的抑制效果时,不仅要考虑滤波器本身及引线对噪声的衰减能力,在高频时还要考虑寄生参数影响。

图1 噪声测试电路
文献[10]提出了一种用于提高EMI滤波器特性的方法,均是基于阻抗匹配情况,即在源、负载阻抗均为50W条件下对平面EMI滤波器进行设计,而当源、负载阻抗并非为50W时,该滤波器有时不仅不能抑制噪声,反而会放大噪声。文献[11]着重研究了存在引线的条件下,谐振峰的变化及其与负载端引线长短的关系。文献[12]提出了散射参数(S参数)的观点,但并未对存在传输线的情况进行详细推导与验证。文献[13,14]较为全面地分析了EMI滤波器的高频特性,并对源、负载阻抗为某一非50W定值时进行研究,但是实际中噪声源阻抗并非是一个定值,而是随着频率的改变而变化。因此,该方法并不具有的通用性。
总之,文献研究并未考虑传输线对源、负载阻抗的影响以及如果噪声的源、负载阻抗同时变化对噪声衰减的影响。
鉴于以上原因,本文以共模EMI滤波器为研究对象,对其抑制效果进行预测,尤其对散射参数法及传统方法进行深入探索,并将其预测结果进行比较,证明本文提出方法的有效性。
1 传输线对噪声负载阻抗的影响
在实际电路中,EMI滤波器负载阻抗为LISN的阻抗及传输线阻抗之和,其值随着频率的变化而变化。
根据传输线理论,假设传输线无损耗,其微单元的等效电路如图2所示[15]。图2中,D、D、D分别为传输线单元长度、单位长度电感、单位长度电容,且D<<(能传输电波长)。
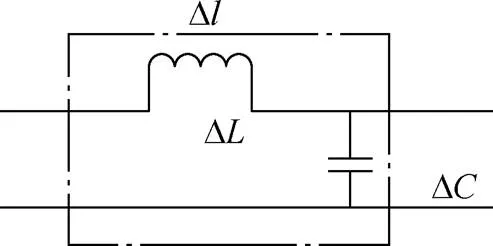
图2 传输线单位长度等效电路
1.1 传输线的等效差模、共模等效参数
图3为传输线的等效电路。如图3中所示,当两个导线通入同向电流时,两导线间不存在电容,仅导线与地之间有电容,即共模电容;而当两导线通入差模电流时,不仅存在导线与地之间的电容,还存在导线与导线之间的电容,即差模电容。
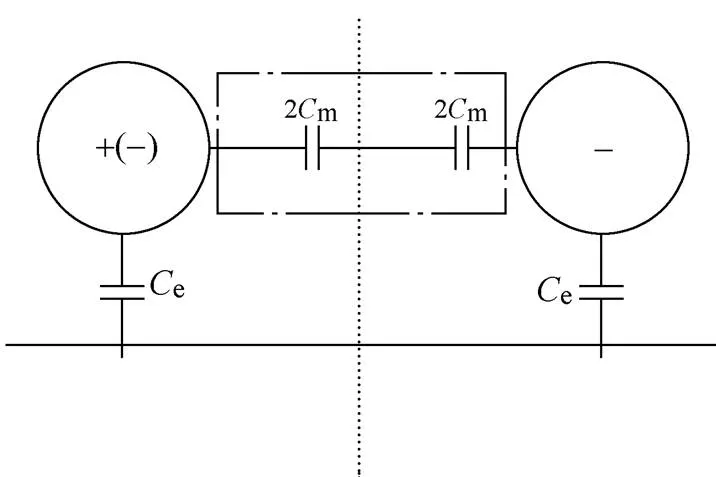
图3 传输线的等效电容
两平行传输线布置如图4所示,对于差模噪声,两连接线流入的噪声电流大小相同、方向相反,即两导线间的虚线为零电位面[16];对于共模噪声,两连接线中的电流大小与方向均相同。
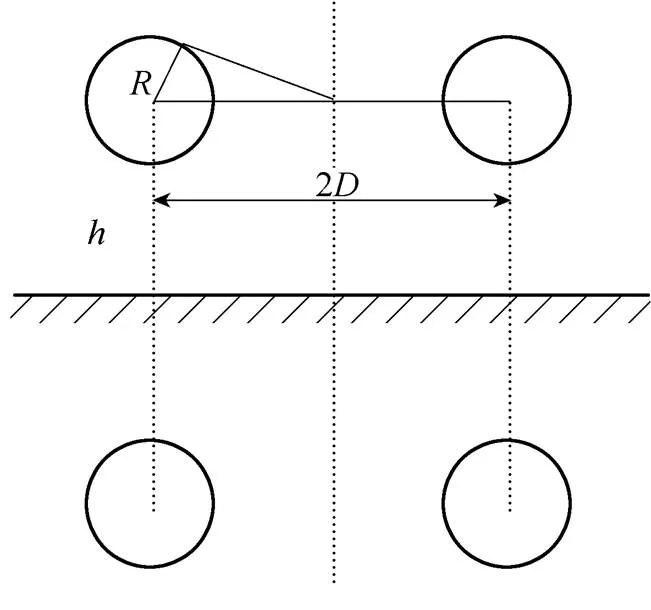
图4 平行传输线
根据传输线理论,可以求得两条传输线间的共模、差模电容,从而差模、共模电感分别为
式中,为电磁波真空中的传播速度,=3×108m/s。
因此,对于共模滤波器而言,其单根传输线与地之间的阻抗为
两根导线与地之间的阻抗为
对于差模滤波器,单根导线与地的阻抗为
两根导线间的阻抗为
1.2 基于传输线理论的噪声负载阻抗分析
传输线的特征阻抗0及传播常数由其分布参数和频率参量决定,假设传输线损耗较小可以忽略不计,则其值分别为
式中,1为单位长度传输线电感;1为单位长度传输线电容,当传输线损耗为0,即=0时,则=j。
图5所示为存在传输线时的滤波器负载阻抗模型。由图5得到传输线上任意一处的电压和电流可以表示为
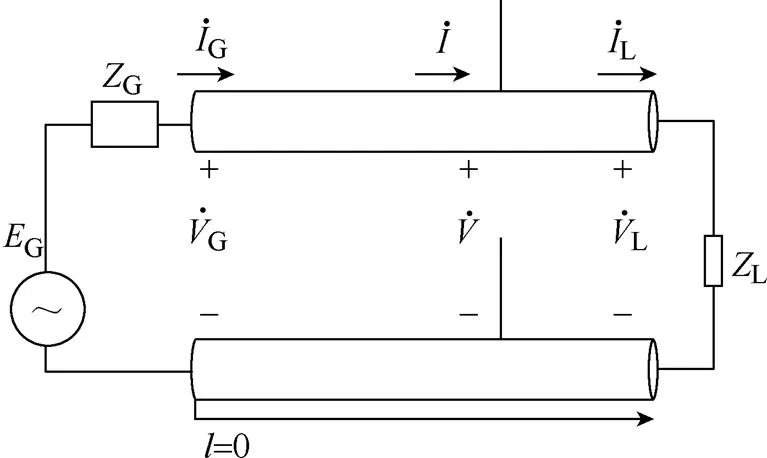
图5 存在传输线时滤波器负载阻抗
同时,有
式中,为传输线的总长度,联立式(11)和(13)可得
根据式(15)及式(16)可知
将1、2代入式(9)、式(10)可分别求出传输线上任意一处的电压与电流值,从而求得输入阻抗in。

(20)
1.3 差模、共模EMI滤波器噪声负载阻抗的测试
为了方便测试,特性阻抗为
式中,OC为开路传输线阻抗;OS为短路阻抗。对应式(8)中,为
以共模滤波器为例,根据测试得开路阻抗约为8 500W,短路阻抗约为0.1W,计算得到0约为100W,由于传输线长为1m,计算出的值,从而可以计算出in=50W。
2 传输线对噪声源阻抗的影响
2.1 基于传输线理论的噪声源阻抗分析
对于噪声源阻抗S而言,由于存在传输线阻抗C,因此,噪声源阻抗不仅包括噪声源自身阻抗,还包括传输线阻抗,其值随着频率的变化而变化。
阻抗的连接方式一般有两种:RLC并联与RLC串联。当RLC并联时,噪声源阻抗与电压可等效为并联结构;当RLC串联时,噪声源阻抗与电压可等效为串联结构如图6所示,对应特性见表1。
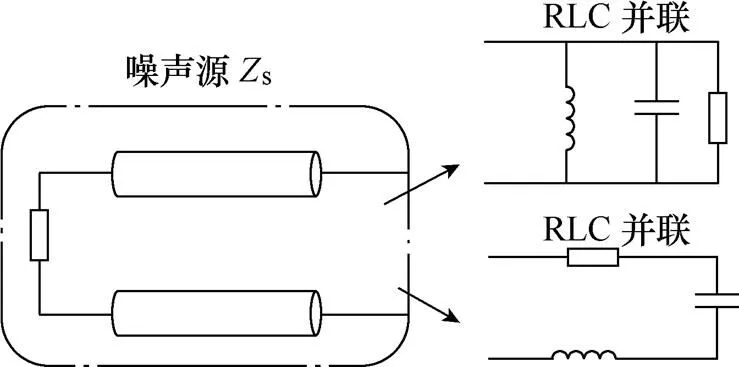
图6 共模噪声源等效结构
表1 RLC串、并联阻抗及特性曲线
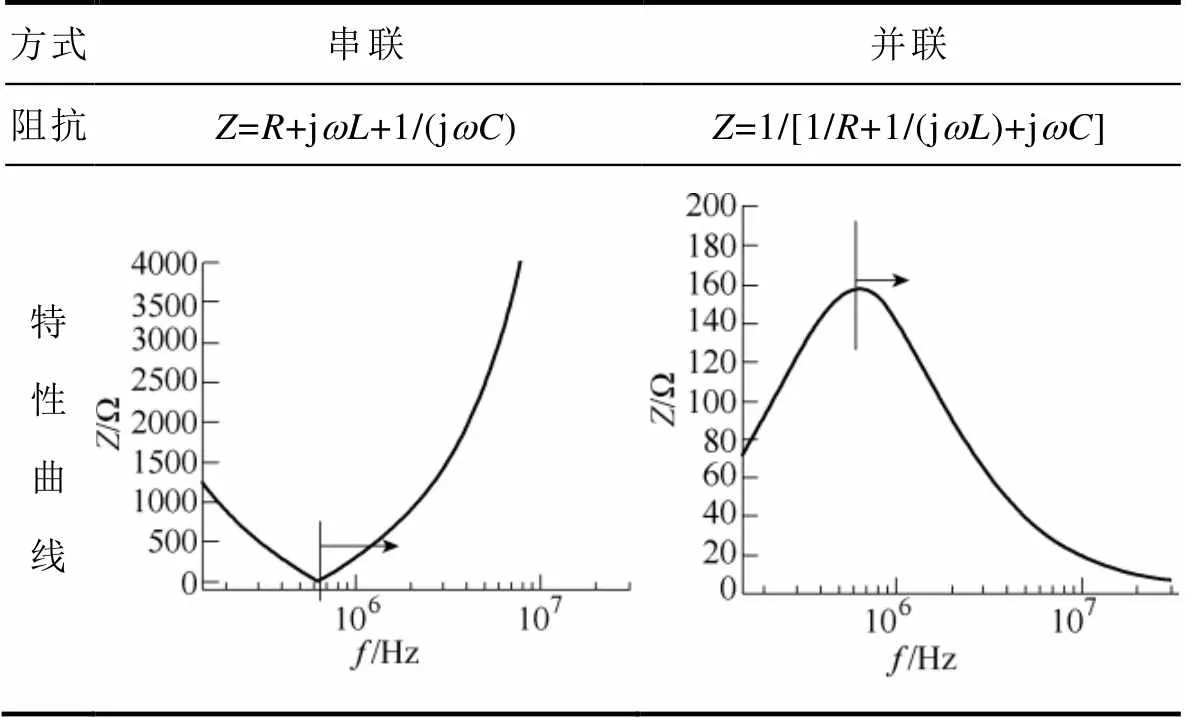
Tab.1 Series and parallel impedance and their characteristic curves of RLC
共模噪声源阻抗多次测试结果如图7所示。测试显示,噪声源阻抗随着频率的增大,先减小,后增大,因此可等效为RLC串联电路,即阻抗与噪声电压串联电路,且曲线在高频段存在一系列的谐振,这是由于传输线存在电感与电容。
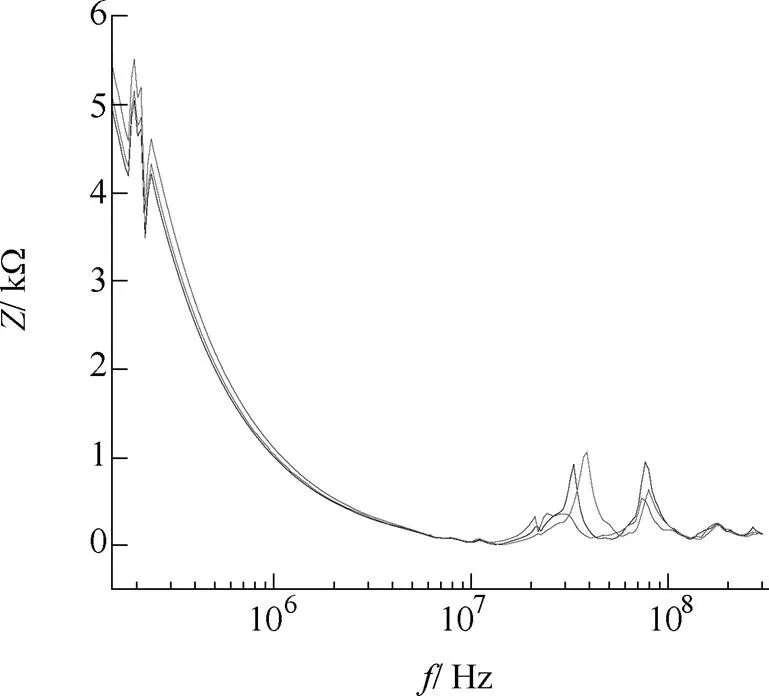
图7 共模噪声源阻抗测试值(多次)
根据以上分析,噪声源阻抗可等效为RLC串联结构,因此等效测试电路如图8所示,EMI滤波器源、负载之间均存在传输线,因此噪声源阻抗为传输线阻抗与负载阻抗之和,可通过阻抗分析仪Agilent 4395A测试得出,即
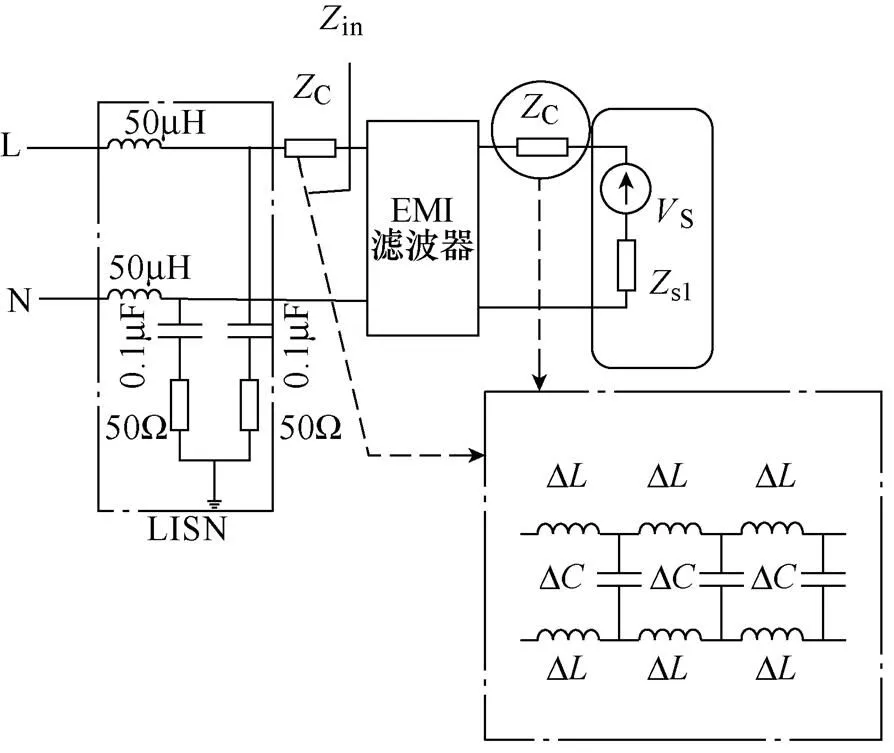
图8 等效测试电路
2.2 差模(DM)滤波器噪声源阻抗
同样,采用以上方法多次测试差模噪声源阻抗测试结果如图9所示,曲线同样与RLC串联结构相似。为了方便等效,同样简化为噪声源与阻抗串联结构。因此,差模噪声源阻抗的测试电路亦如图8所示。其中,高频段的一系列谐振也是由传输线引起。
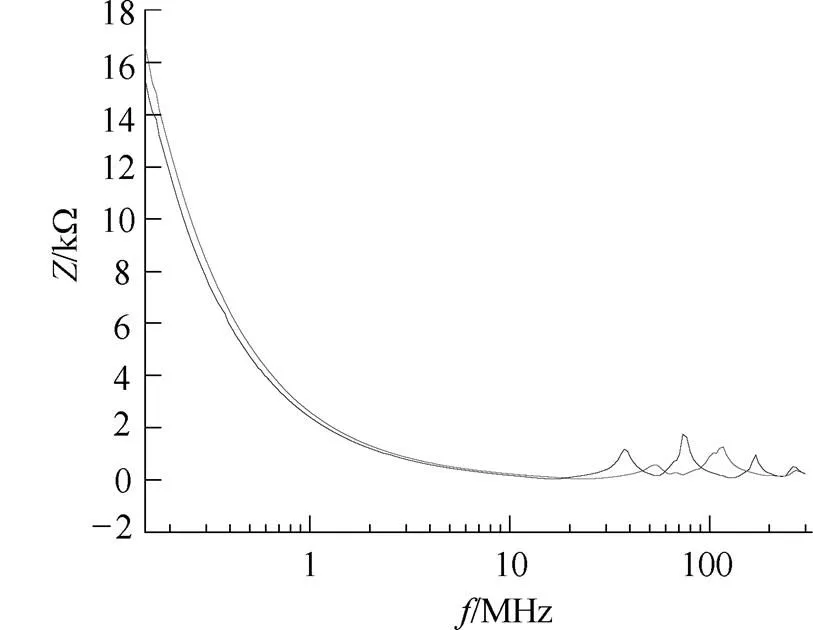
图9 差模噪声源阻抗值(多次)
2.3 阻抗法条件下EMI滤波器衰减
设计的EMI滤波器电感为220mH,共模电容为2.2pF,差模电容为47nF,因此,实际条件下共模滤波器与差模滤波器的衰减和阻抗法预测的EMI滤波器衰减如图10所示。图10a表示共模滤波器的实际衰减与阻抗法预测曲线的比较,可见采用阻抗法来预测EMI滤波器的噪声时,在低频段吻合较好,预测噪声曲线在实际噪声衰减曲线的中间位置,这是因为在低频段自寄生参数及互寄生参数的影响小。但是随着频率的升高,高频段拟合特性越来越差,由于寄生参数随频率的变化而变化,尤其是互寄生参数的存在,使得阻抗法无法再很好地预测噪声衰减。同理,图10b为差模滤波器的阻抗法预测曲线与实际衰减曲线,与共模滤波器类似,在低频段吻合较好,高频段偏离较大。因此,阻抗法一般用来预测低频的噪声衰减比较准确,而高频的衰减则需要寻找其他方法来进一步验证。

(a)共模滤波器
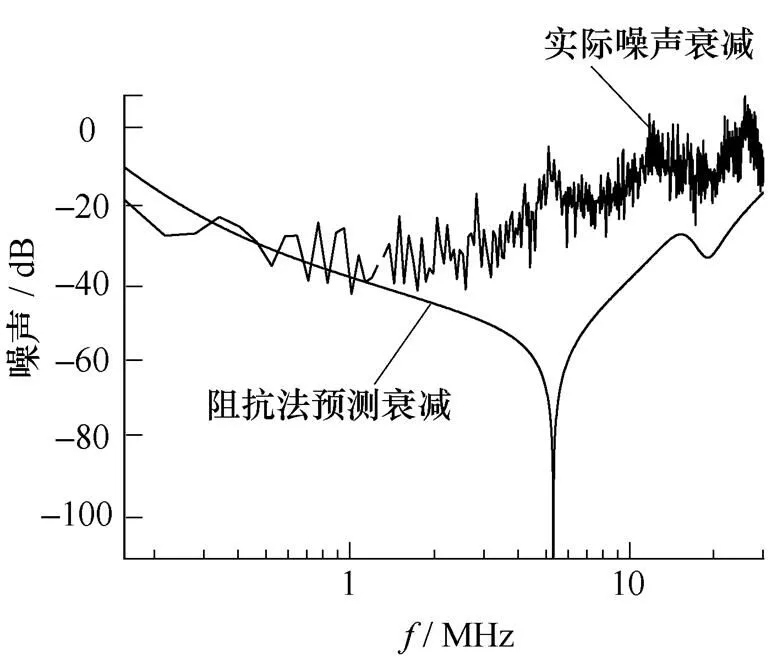
(b)差模滤波器
图10 阻抗法与实际噪声比较
Fig.10 Comparison of the actual measured noise and predicted noise with impedance method
3 S-参数法对EMI滤波器衰减预测
3.1 传统EMI滤波器S参数
无源EMI滤波器网络在小信号激励下工作状态近似为线性网络,如图11所示。采用S参数来预测EMI滤波器的衰减时,根据传输线理论,可得其插入增益(插入损耗)为[12]

图11 小信号激励下的EMI滤波器
针对单级EMI滤波器,若源、负载阻抗改变,则反射系S和L会发生改变,从而改变噪声衰减。
然而当噪声源与EMI滤波器之间及EMI滤波器与负载之间存在引线,且引线长度无法忽略时,则电压衰减不再如式(24)所示,需考虑引线对其影响。多级S参数计算过程如下:

EMI滤波器的 T参数矩阵S参数 → 滤波器与负载间引线S参数↓ → 噪声源与滤波器间引线S参数 →
考虑元件间的相互耦合,差模、共模EMI滤波器均可以等效为T形结构,如图12所示。采用网络分析仪测得S参数,代入式(25)~式(27)即可求出其等效T矩阵的各个阻抗。
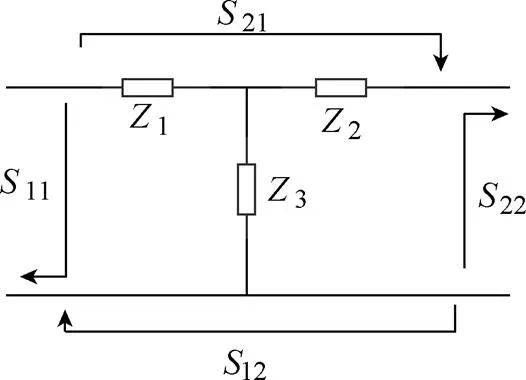
图12 S参数等效电路
根据图12二端口网络,可得理想条件下单级EMI滤波器的T参数矩阵。
然而,实际中EMI滤波器与负载及噪声源之间均存在传输线,因此,预测噪声源衰减时,还要考虑其两侧传输线对噪声衰减的影响,所以考虑引线阻抗的EMI滤波器传输矩阵如图13所示,其表达式为
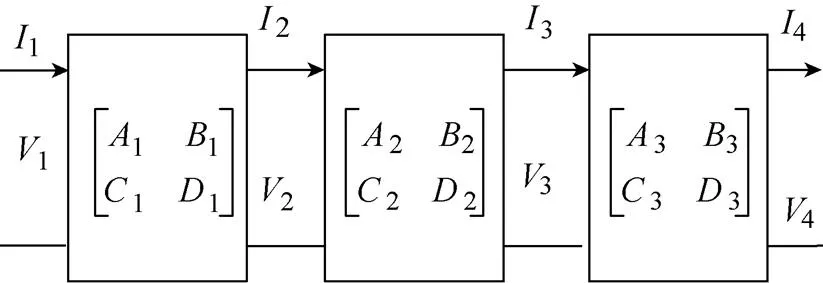
图13 考虑引线阻抗的EMI滤波器传输矩阵
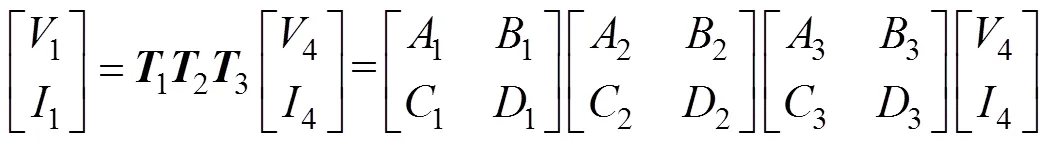
在非理想条件下,可先得出滤波器与传输线总的T参数矩阵,如式(32)所示,从而进一步得到噪声衰减量。其中,矩阵1为噪声源与EMI滤波器间传输线矩阵,2为单级EMI滤波器自身矩阵,3为EMI滤波器与负载间传输线矩阵。
以共模滤波器为例,采用网络分析仪可得其S参数值如图14所示,差模则不再详细列出。
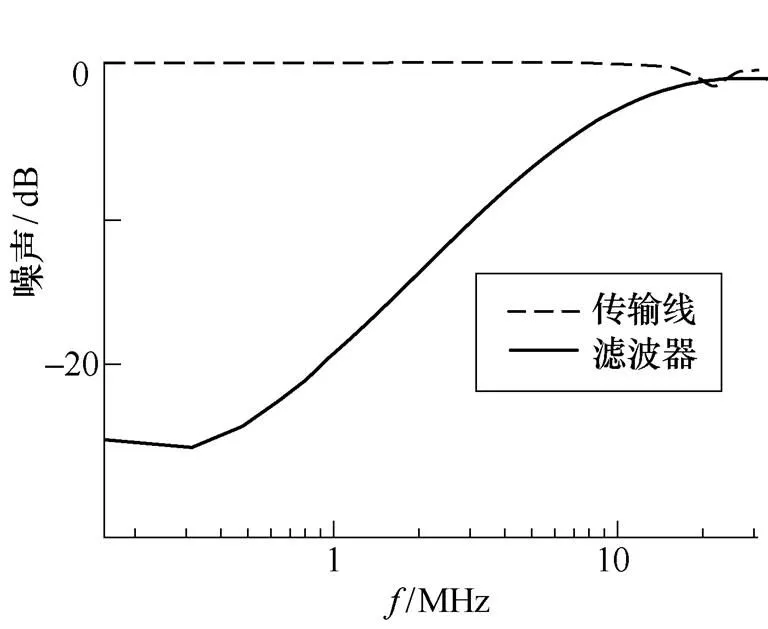
(a)11
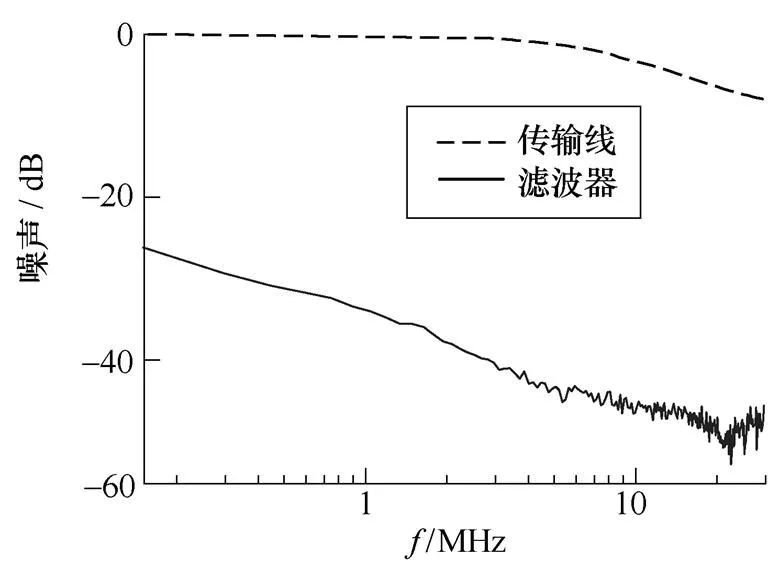
(b)21
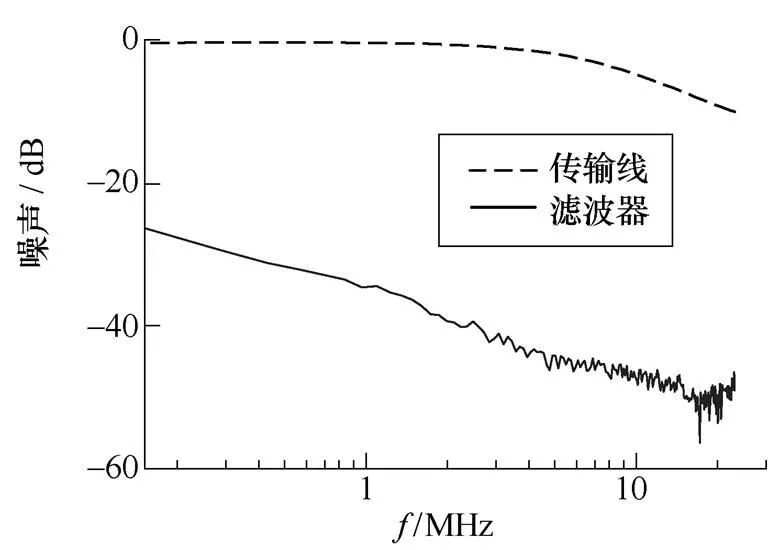
(c)12
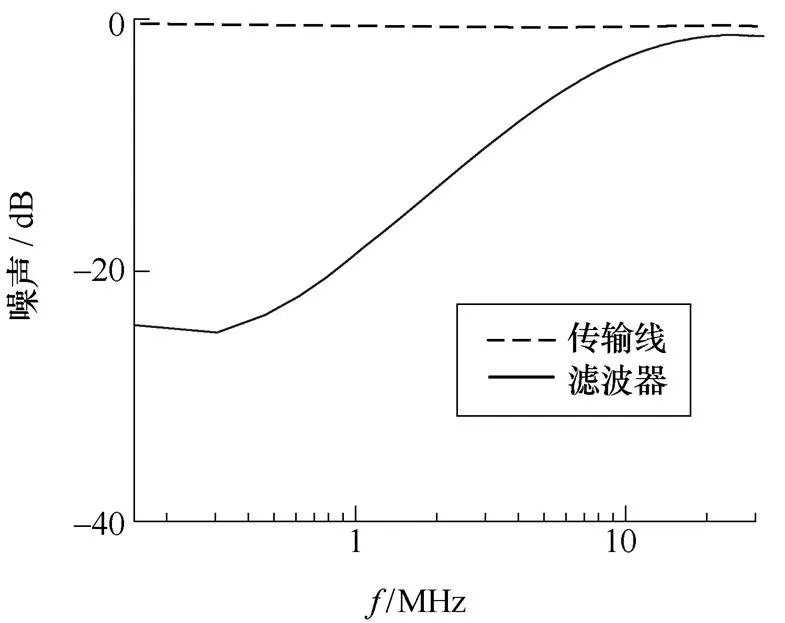
(d)22
图14 传输线及滤波器S参数
Fig.14 S parameters of transmission line and EMI filter
3.2 基于包络线的噪声预测与测试
实验中,网络分析仪用于在普通环境下实现对噪声的预测,而实际噪声衰减是在电磁屏蔽室中进行的,因此噪声测试环境变化使得滤波器噪声幅值衰减存在随机性。尤其是高频段,会使得实际衰减曲线与预测曲线的谐振点无法一一对应,因此,本文提出了“包络线”的概念,取实际噪声衰减的最大值与最小值点,连起来所得的曲线为该噪声的包络线,只要预测曲线基本落于实际衰减曲线的包络线内,就可认为此次预测具有一定的现实意义。
包络线包括包络线上限(最大值)及包络线下限(最小值),其中,包络线上限表达式为
式中,为所选点序号;为噪声曲线所取点数。当同时大于两侧点的取值时,即为噪声的包络线上限参考点,如此依次取出频率段150kHz~30MHz之间的参考点,连接即可得到包络线上限。
类似地,当X同时小于两侧点的取值时,X即为噪声的包络线下限参考点为
若包络线上、下限取点过多,包络线的变化过快不利于图形分析时,则可以通过循环上述步骤,进一步筛选所取的参考点,直到满足绘制要求为止。
本文以分立元件组成的EMI滤波器为研究对象,其测试电路如图15所示。

图15 实际衰减测试电路
共模滤波器的实际噪声曲线与S参数预测曲线如图16a所示,图16b则为实际衰减的包络线。
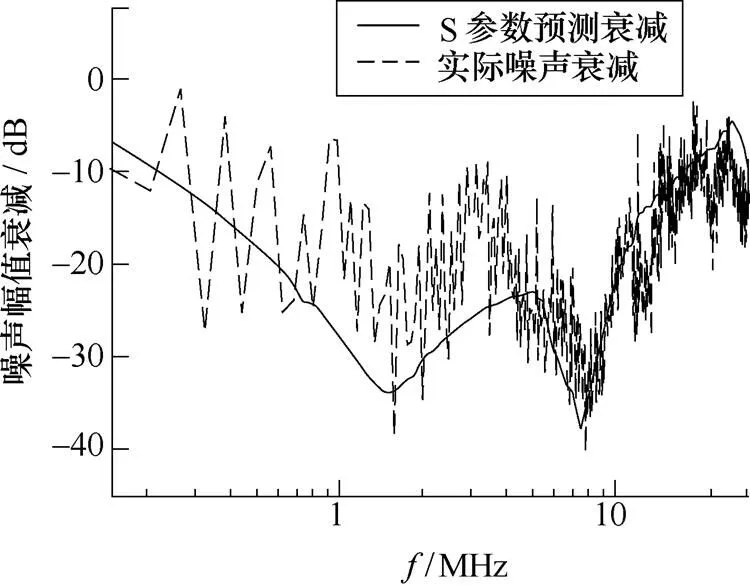
(a)共模实际衰减曲线与S参数预测曲线
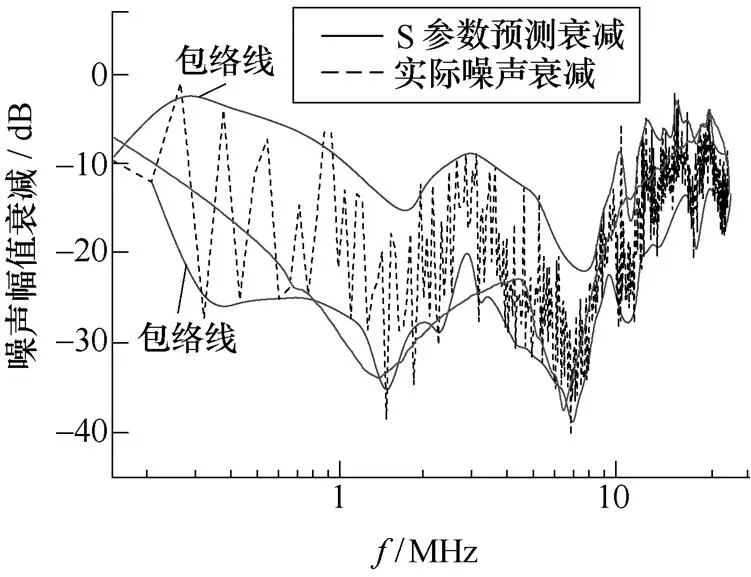
(b)共模滤波器包络线
图16 共模滤波器S参数法与实际噪声衰减比较
Fig.16 Comparing the actual measured noise and predicted noise by S-parameters method for CM filter
同样,差模滤波器的实际噪声曲线与S参数预测曲线,以及实际衰减包络线如图17所示。
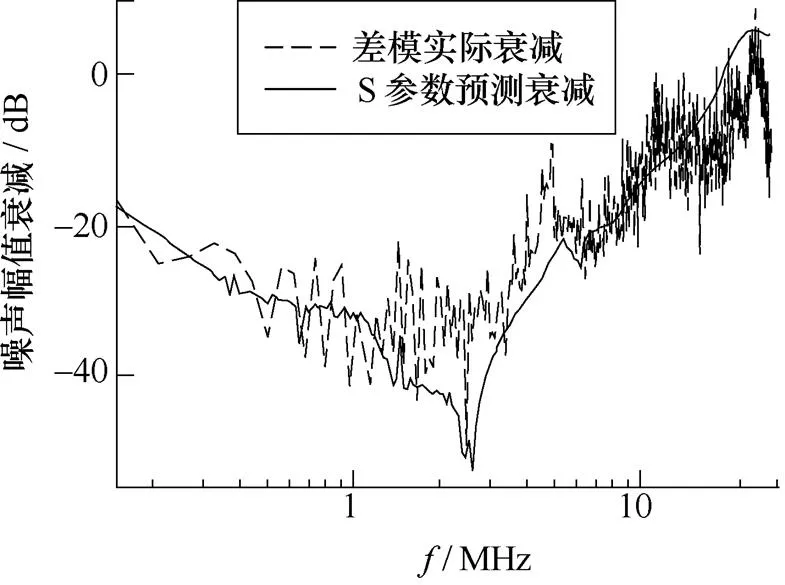
(a)实际衰减曲线与S参数预测曲线
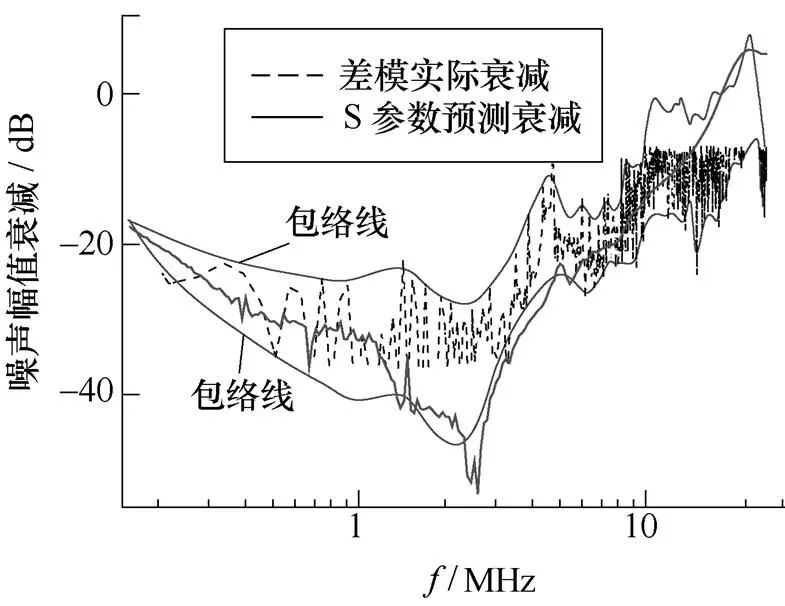
(b)滤波器包络线
图17 差模滤波器S参数法与实际噪声衰减比较
Fig.17 Comparison of the actual measured noise and predicted noise by S-parameters method for DM filter
由图16和图17可见,处于低频段时,与阻抗法预测曲线类似吻合较好,S参数预测曲线位于实际噪声衰减曲线的中间位置;随着频率的升高,预测曲线虽不再位于实际测量曲线的中心位置,但仍然基本处于包络线内,因此采用S参数法来预测EMI滤波器的衰减与实际测量值比较接近,尤其在高频段拟合效果远远优于阻抗法。同时,基于以上分析可知,S参数法同样可以用于多级级联EMI滤波器的衰减预测。
为了进一步说明包络线在噪声比较中的重要意义,本文测试了另外一个差模滤波器,如图18所示,其实际衰减曲线与采用S参数的噪声预测曲线如图19所示。

图18 差模滤波器
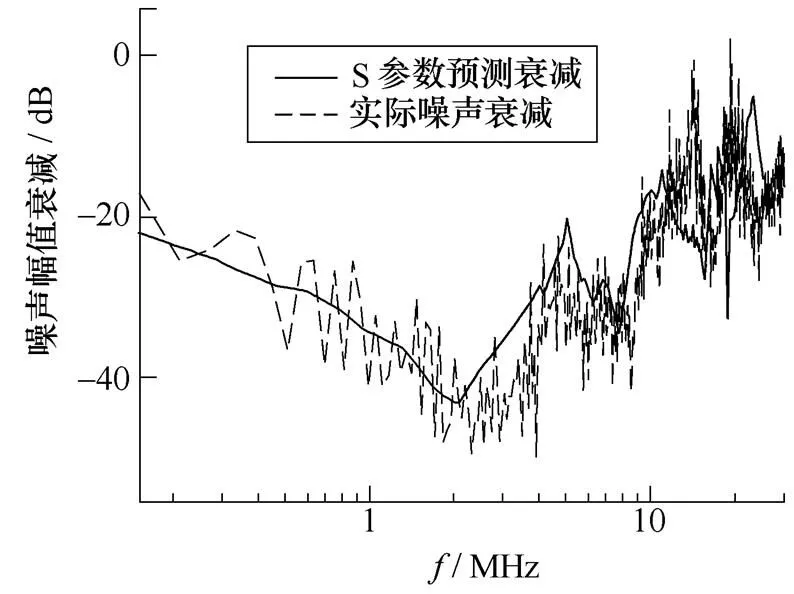
(a)实际衰减与S参数预测
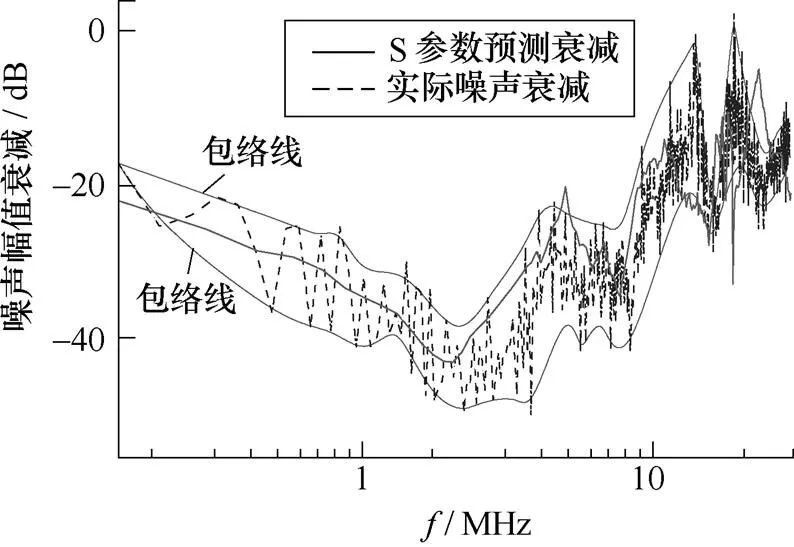
(b)包络线
图19 另一差模滤波器S参数法与实际噪声衰减比较
Fig.19 Comparison of the actual measured noise and predicted noise by S-parameters method for another DM filter
图19中低频段吻合曲线均较好,预测曲线在实际噪声曲线的中间位置,这与之前的分析相符。比较图17与图19,前者采用整个频段测试的方法,而后者采用网络分析仪对噪声频率分段测试,可见随着频率的升高,当取点数越多时,噪声曲线波动越明显,峰值点也越多。这种峰值点与单位频段内取值点数有关,还与噪声测试环境有关,因此采用包络线对噪声衰减预测能力评估时,可忽略部分由以上两种原因产生的峰值点,从而使得评估过程具有更好的普遍性与现实意义。
4 结论
本文以共模EMI滤波器为研究对象,基于S参数法及阻抗法来预测其电压衰减,并与实际电路的衰减进行比较,得到以下结论:
1)由于传输线的存在,EMI滤波器的源、负载阻抗不匹配。此时,理想条件下的S参数对传统滤波器电压衰减的预测方法不再适用,因此本文提出了一种改进后的S参数预测法,该方法考虑了传输线对噪声衰减的影响。
2)噪声预测有两种方法:S参数法及阻抗法。通过实验可见,由于S参数法不仅考虑了元件的寄生参数,还考虑了元件间的互寄生参数,因此在高频段拥有更好的衰减特性。
3)S参数法可分别测试传输线和滤波器的S参数,通过T矩阵进行计算,此方法同样适用于计算多级EMI滤波器的噪声衰减,为多级EMI滤波器噪声抑制的预测提出了一种新的方法。
参考文献
[1] 钱照明, 程肇基. 电力电子系统电磁兼容设计基础及干扰抑制技术[M]. 杭州: 浙江大学出版社, 2000.
[2] Fang Luo, Dong Dong, Dushan Boroyevich, et al. Improving high frequency performance of an input common mode EMI filter using an impedance mismatching filter[J]. IEEE Transactions on Power Electronics, 2014, 29(10): 5111-5115.
[3] 金亮亮, 周荔丹, 姚钢, 等. 适用于并网逆变器的新型LCL滤波器[J]. 电力系统保护与控制, 2016, 44(11): 1-8.
Jin Liangliang, Zhou Lidan, Yao Gang, et al. A novel LCL filter adopted in grid-connected inverter[J]. Power System Protection and Control, 2016, 44(11): 1-8.
[4] Sheng Ye. New EMI filter design methods for DC-DC and AC-DC switching power supplies[D]. Kingston: Queen’s University, 2003.
[5] 马伟明. 独立电力系统及其电力电子装置的电磁兼容[M]. 武汉: 武汉水利电力大学出版社, 2000.
[6] 陈恒林, 陈玮, 冯利民, 等. 通过改变噪声源阻抗抑制高频共模噪声[J]. 电力电子技术, 2006, 40(6): 124-125.
Chen Henglin, Chen Wei, Feng Limin, et al. High frequency common mode EMI noise suppression for switching converters by impedance control[J]. Power Electronics, 2006, 40(6): 124-125.
[7] Wang Shuo, Fred C Lee, Willem Gerhardus Odendaa. Characterization and parasitic extraction of EMI filters using scattering parameters[J]. IEEE Transa- ctions on Power Electronics, 2005, 20(2): 502-510.
[8] Bo Hu, Kye Yak See, Weng Yew Chang Richard. Evaluation of ferrite core EMI suppression under realistic working conditions[C]//2008 Asia-Pacific Sympsoium on Electromagnetic Compatibility, Singapore, 2008: 774-777.
[9] 陈恒林. EMI滤波器高频建模一寄生效应研究[D]. 杭州: 浙江大学, 2007.
[10] Huang Huifen, Deng Liangyong, Hu Binjie, et al. Techniques for improving the high-frequency performance of the planar CM EMI filter[J]. IEEE Transactions on Electromagetic Compatibility, 2013, 55(5): 901-908.
[11] Fang Luo, Dushan Boroyevich, Paolo Mattavelli. Improving EMI filter design with in circuit impedance mismatching[C]//Twenty-Seventh Annual IEEE, Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, 2012: 1652-1658.
[12] 石磊磊, 王世山, 徐晨琛. 二端口网络散射参数理论及其在平面EMI滤波器测试中的应用[J]. 电工技术学报, 2013, 28(2):78-85.
Shi Leilei, Wang Shishan, Xu Chenchen. Theory of scatter parameters of two port network and its application in the test of planar EMI filter[J]. Transactions of China Electrotechnical Society, 2013, 28(2): 78-85.
[13] 张佳佳, 张逸成, 韦莉, 等. 基于插入损耗的噪声源阻抗修正计算方法[J]. 电工技术学报, 2015, 30(4): 80-87.
Zhang Jiajia, Zhang Yicheng, Wei Li, et al. A revised calculation method for noise source impedance based on insertion loss[J]. Transactions of China Electro- technical Society, 2015, 30(4): 80-87.
[14] 洪博, 王莉, 毛健美, 等. 一种航天器一次母线故障在线检测定位方法[J]. 电工技术学报, 2016, 31(5): 118-125.
Hong Bo, Wang Li, Mao Jianmei, et al. An online detection and locating method for spacecraft bus faults[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 118-125.
[15] David M, Pozer. Microwave engineering[M]. 3rd ed. Beijing: Publishing House of Electronics Industry, 2008.
[16] 冯慈璋. 电磁场[M]. 西安: 西安交通大学出版, 1979.
[17] Wang Shuo. Characterization and cancellation of high-frequency parasitics for EMI filters and noise separators in power electronics applications[D]. Virginnia: Virginia Polytechnic Institute and State University, 2005.
Predicting the Suppression Effect of EMI Filter Based on the S-Parameter Method
(Jiangsu Key Laboratory of New Energy Generation and Power Conversion Nanjing University of Aeronautics and Astronautics Nanjing 210016 China)
Electromagnetic interference (EMI) filter is an important component to suppress the conducted EMI noise, especially the EMI filter with high performance. Based on the transmission line theory, the common mode (CM) parameters and differential mode (DM) parameters of parallel transmission lines are obtained, and the source and load impedances are received through calculation and test. Furthermore, the insertion loss (IL) can be calculated by the impedance method. However, in the high frequency, the parameters of EMI filter and transmission line involve not only the self-parasitic parameters but also the mutual parasitic parameters. These mutual parasitic parameters are very difficult to calculate or be equivalent by the impedance method. Therefore, the parameters of CM and DM filters with transmission line are explored. Then, according to the transmission line theory, the noise source and load impedance are calculated. Taken CM filter as an example, the attenuation of noise is predicted by the impedance method, and is compared with the actual test value. However, the prediction on attenuation of noise is inaccurate at high frequency. Thus, this paper further presents a method (S parameter) to predict the attenuation accurately under the conditions of impedance mismatch, where the key of this method is the incident and reflected waves. It is shown that due to the consideration of the interaction among the parasitic elements, the S-parameter method has better high-frequency performance.
EMI filter, differential noise, common noise, impedance mismatching, S-parameters
TM93
王世山 男,1967年生,博士,副教授,研究方向为电力电子系统的电磁兼容,电气设备的多物理仿真技术。
E-mail: Wangshishan@ nuaa.edu.cn(通信作者)
龚 敏 女,1989年生,硕士研究生,研究方向为电力电子系统电磁兼容。
E-mail: 824022597@qq.com
2015-07-25 改稿日期 2016-05-07
国家自然科学基金(51177071),台达环境与教育基金会《电力电子科教发展计划》(DREK2013004),江苏高校优势学科建设工程项目,南京航空航天大学研究生创新基地(实验室)开放基金(kfjj201412)和中央高校基本科研业务费专项资金资助项目。

