基于粗糙集理论和生命初态信息的继电器寿命预测方法
李玲玲 张士暖 李志刚 贺鹏举
基于粗糙集理论和生命初态信息的继电器寿命预测方法
李玲玲 张士暖 李志刚 贺鹏举
(河北工业大学电磁场与电器可靠性省部共建重点实验室 天津 300130)
工作寿命是表征产品可靠性的重要特征量。对于继电器这类长寿命产品,以寿命为指标进行产品筛选的方法目前还未得到深入研究。近来通过对继电器寿命试验数据进行分析发现:继电器个体的寿命与其生命初期的性态有关,初期性态较好的个体其寿命也较长,反之则寿命较短。本文基于这一发现提出了继电器的个体寿命预测与筛选方法,即首先通过寿命试验获取一组样本在生命初期的性能参数值与寿命值,然后利用粗糙集理论中的属性约简提取一组与寿命相关的性能参数,并建立一组寿命决策规则。此后对于任一同型产品,只要测出其生命初态信息即可根据这组规则预测其寿命,进而完成以寿命为指标的继电器产品筛选。本文最后进行了实例分析,结果表明了该方法的有效性。
继电器 生命初期特征 寿命预测 产品筛选 粗糙集理论
0 引言
工作寿命是表征工业产品可靠性的重要特征量。对于继电器而言,不同行业、系统和设备对其工作寿命有着不同要求,因此很多时候需要以寿命为指标进行继电器的筛选。例如在车辆系统中,扬声器继电器要求百万次左右的工作寿命,前灯继电器50万次,而其他一般的继电器达3~10万次即能满足需要[1]。特别地,当继电器服役于某些对可靠性要求极高、一旦投入使用即不易修复甚至根本无法修复的系统(例如太空站、海上石油平台和人造卫星等)时,每个继电器个体都被要求拥有比其所服役的系统更长的工作寿命。为此不得不进行历时较长、条件严苛的筛选试验,从而占用大量人力物力并产生高昂费用,况且这种历时较长的筛选试验本身也会减少继电器个体的剩余寿命,使其有效服役期缩短。随着我国太空技术与军工技术等的迅猛发展,当前迫切需要一种以寿命为指标对包括继电器在内的电子电器进行筛选的方法,且该方法不会过多压缩其有效服役期。
以寿命为指标的产品筛选首先需要对产品寿命做出预估、预测。当前,产品寿命预测的方法可分为两类:一类是基于抽样检测理论,根据样本的寿命数据推测整体的寿命分布以及与寿命有关的可靠性特征量(如平均寿命、中位寿命等)。这类方法适用于批产品而非个体的寿命预测,对于以寿命为指标的产品筛选意义不大,因为即使是同一批次的产品,不同个体的寿命也是有差别的,表征整体性能的寿命指标并不能充分表达个体的情况。另一类方法是根据产品个体的性能参数变化特征推测其寿命,此类方法建立在产品个体的性能退化机理之上,可以体现同一批次下不同产品个体的寿命差别,故其适用对象为产品个体。
在上述第二类方法中,当前的研究大多集中于基于神经网络[2]、回归分析[3,4]、小波和ARMA分析[5]等数学方法建模的预测。这类数值型预测方法所需数据量较大,计算过程复杂。事实上,在为太空站这类对可靠性要求极高的系统筛选基础电子器件(例如继电器)时,并不需要确切掌握每个器件的工作寿命,而只要求这些器件的寿命长于系统自身的服役期,这种情况下,用于器件筛选的寿命预测应侧重于定性而非定量。另外,较复杂的自控系统所含继电器成百上千,例如某型军用运输机采用了300多只航天继电器,某大型人造卫星采用的继电器数量达1 500多只[6],如果每个继电器都基于数值型预测方法进行筛选,则计算量太过庞大。简言之,以系统寿命为筛选依据的基础器件寿命预测不便于采用上述数值型预测方法。
通过对长期所积累的不同型号继电器的寿命试验数据进行分析,一个规律近来被发现,即:继电器个体的寿命与其生命初期的性态有关,初期性态较好的个体其寿命也较长,反之则寿命较短。本文基于这一发现,运用粗糙集理论建立了继电器产品初期性能参数和寿命的决策表,然后根据所建立的决策表和继电器的初期性能参数信息即可预测继电器个体的寿命等级(即寿命的大致范围),最终实现以寿命为指标的继电器产品筛选。
1 继电器寿命试验数据特征分析
继电器的触点是最易侵蚀破坏的部位,其故障率占总故障率的80%以上[7]。继电器通电后,其触点并不是马上就达到稳定闭合状态,而是要经历弹跳和动态接触这两个过程。在触点的弹跳过程中,弹跳时间是刻画这一过程的重要参数;而在动态接触过程中,动态波动时间和动态接触电阻则是刻画该过程的重要参数;触点稳定吸合后的性能则由静态接触电阻刻画。动态接触电阻是指触点闭合或断开时,随触点压力大小而变化的接触电阻;静态接触电阻是指触点稳定闭合状态下的触点间电阻。因动态接触电阻、静态接触电阻不易直接测量,故通过测量触点间的动态接触压降峰值(即动态峰值压降)、静态接触压降来分别替代。
本文选取了12只某型号电磁继电器作为试品,分三组进行了可靠性寿命试验(每只试品选择一对触点),同步监测并记录了这些试品随触点动作次数变化的四个性能参数(弹跳时间、动态波动时间、动态峰值压降和静态接触压降)。12只试品的寿命实测值和估算值见表1,这里注释如下:
(1)试品寿命由其触点动作次数表示,“次”表示继电器试品正常工作时其触点通、断各一次。
(2)三组试品分别在-20℃、20℃、55℃三种环境温度下采用定时截尾方式各自进行试验,定时分别为330万次、492万次和140万次。至试验截止时仅第5、6号试品失效,寿命分别为232万次和242万次。失效类型前者为静态接触电阻大幅增加而后者为触点黏连,其余试品均未失效。
(3)试验中,试品的线圈加额定电压,但触点并非带额定负载,而是带载一个微弱电信号,因此表中的“寿命”并非严格意义上的电寿命或机械寿命。但因触点实际所带负载远小于额定值,故表中试品的寿命值应更接近于其机械寿命。
(4)本文方法须对试品做全寿命试验,以获得每个试品的寿命值。但受试验条件所限,目前仅对该型号继电器的12个试品分组进行了定时截尾试验,未获得全部试品工作寿命的实测值。为填补缺失的信息,本文采用小波包变换与RBF神经网络相结合的方法[8]对各试品的各项性能参数进行了预测,一旦发现试品的任一性能参数预测值超过限定值则视其为失效,由此获得了各试品寿命的估算值,见表1,相关的数据处理过程从略。
表1 三种温度下继电器试品的寿命实测值和估算值
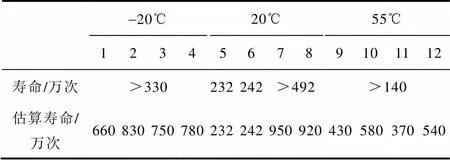
Tab.1 The actual and estimated life of the tested relays at the temperature of -20℃, 20℃ and 55℃
由表1数据可知:即使在同一环境温度下,各试品的寿命也会出现较大差别。例如试品5、试品7虽然都工作于20℃,但前者通断232万次即失效而后者工作至492万次仍完好,估算其寿命可达到950万次。经对试验数据进行全面分析发现,试品在寿命指标上的优劣于其生命初期的性能参数上即有所体现,或者说,试品在生命初期的性态好坏预示着其工作寿命的长短。图1、图2分别为20℃下试品5和试品7在生命初期关于动态波动时间、静态接触压降这两项性能参数的对比。
由图1、图2两图易见,寿命较短的试品5在生命初期的动态波动时间较大,在生命最初时刻的静态接触压降也较大;而寿命值相差较大的试品5和试品7在生命最初时刻之后的一段时间内,其静态接触压降却相差不大。
总结表1、图1和图2,可知继电器的个体寿命与工作温度以及生命初期的性态有关,初期性态较好的个体其寿命也较长,反之则寿命较短。然而,继电器的个体寿命受多个因素影响,并非所有的影响因素都是同等重要的,甚至有些是不必要的、冗余的,这些不必要的因素不但会增加预测的运算量,还会干扰预测结果。对此,可借助于粗糙集理论删减冗余信息。
2 粗糙集理论的基本知识
粗糙集理论由波兰学者Z.Pawlak创建于1982年,其主要优势是不需任何先验知识与信息,被作为一种数据挖掘和知识发现的有力工具而成功应用在模式识别、机器学习和过程控制等领域。
在粗糙集理论[9]中,知识被认为是一种对研究论域对象具有分类能力的信息。知识表达系统也称为信息系统,多元组表示的信息系统如下:=<,,,>,其中为研究对象的非空有限集,称为论域;为属性的非空有限集,,为条件属性,为决策属性;是属性值的集合,,V为属性的值域;是一个信息函数,它为每个对象的每个属性赋予一个信息值:,,。
设是上的一个等价关系,/表示的所有等价类组成的集合。若且,则(即中所有等价类关系的交集)也是一个等价关系,称为上的不可区分关系,记为ind()。这样,表示与等价关系族相关的知识。
定义1 上近似、下近似与正域
称为集合的正域。
定义2 知识的约简与核
约简是与信息系统的属性全集具有相同基本集的最小属性子集。令信息系统=<,,,>,设,如果是独立的,且ind()=ind(),则是的一个约简。
属性的核是信息系统的属性集的所有必要属性构成的集合,记为core(),常称为的核。记red()为的所有约简集合,则有
即的所有约简的交集构成的核。
定义3 决策规则可信度
3 基于粗糙集理论的继电器寿命预测方法
基于粗糙集理论的预测过程可划分为两大步骤,即决策规则的建立与匹配,对应于知识工程中的知识获取与使用。以下对这两个步骤进行分述。
3.1 继电器寿命决策规则的建立
决策规则的建立(或称获取)方法如下:
(1)建立继电器寿命预测的信息系统。将继电器寿命试验中的相关数据视为信息系统=<,,,>,其中,表1中的试品为研究对象;属性集=∪,其中条件属性由试验条件以及用于描述继电器触点性态的四个性能参数组成,且有={环境温度,弹跳时间,动态波动时间,动态峰值压降,静态接触压降}={1,2,3,4,5},继电器试品寿命作为决策属性集,有={继电器寿命};属性值的集合通过试验测试得到。
信息系统的数据经常是以关系表的形式给出的。关系表的每一行对应一个具体的研究对象,每一列代表某个属性不同的属性值。在粗糙集理论中,称这个关系表为决策表。继电器寿命预测中任意一个试品的不同属性值构成了决策表中的一行,全部试品的同一属性值构成了决策表中的一列。运用粗糙集理论处理决策表时,要求决策表中的值用离散数据表示。然而继电器产品寿命预测问题中的条件属性2~5和决策属性的值域都是实数域上的一个连续区间,故需对这些属性的值进行离散处理。常用的离散化方法包括经验法、等距离散化、等频离散化、基于布尔逻辑与粗糙集相结合的离散化、基于属性重要性的离散化方法等[10]。对属性值离散化后形成原始决策表。
(2)继电器寿命决策表的约简。原始决策表中含有5个条件属性,但并非所有的条件属性都是同等重要的,甚至有些是不必要的、冗余的,不加删减地选用所有条件属性不但会增加计算量,还可能引入无关的随机信息影响预测结果,因此在导出决策规则之前需先进行属性约简。常用的约简算法有基于区分矩阵的算法[11]、基于属性依赖度的算法[12]、基于分类质量的算法[13]和基于信息熵的算法[14]等。不同算法的特点不同,约简结果也不尽相同,但约简所得的核是一致的。经过属性约简,可得到对继电器寿命最有表征力的最简属性集,该集合保留了与原决策信息系统具有相同决策能力的条件属性。实际预测中仅考虑约简后的条件属性即可。
(3)继电器寿命决策规则的建立。最简决策表只是原有知识表达系统的精简表达,并没有形成有效的决策规则。产生决策规则通常有两种方式:一种方法是将约简后的决策表直接用产生式规则表示出来,并给出每条规则的可信度,这样得到的决策规则即是标准决策规则;另一种为了提髙决策规则与新对象匹配的可能性,在生成标准决策规则后,采用近似规则生成算法增加规则数量[15]。近似决策规则是提高决策规则对新对象的匹配能力的一种方法,然而在分类系统的实际应用中,仍然会经常发生新对象找不到匹配规则的现象,此时需要恰当的规则匹配算法实现决策规则与被预测对象的匹配。
3.2 继电器寿命决策规则的匹配
对继电器产品的寿命预测,实际上是根据被预测对象的条件属性进行规则匹配,把获得匹配的规则结论中关于继电器寿命的值赋给待预测产品,以此作为该产品的寿命预测值,这里,继电器的寿命预测值是一个区间值而非一个确定的实数。
被预测对象和决策规则的匹配分为以下几种情形(类似问题在其他一些文献[16]中也被讨论过):①对象与一条规则相匹配;②对象与多条规则相匹配,且结论相同;③对象与多条规则相匹配,但结论不同;④对象与任一规则均不匹配。
情形①和②的预测结果是确定的;情形③规则之间有冲突,即条件一致,结论不同,因此预测结果有一定的可信度,但并不完全确定。可用投票法、对象跟踪法等方法[17]解决;在情形④中,不存在与被预测对象相匹配的规则。目前解决此类问题的主要方法有部分匹配法和相近规则法。部分匹配法是将被预测对象的部分属性与决策规则进行部分匹配,而相近规则法则是通过某种算法从决策规则中找出与预测对象属性最接近的决策规则。此外还有其他一些规则匹配法,例如文献[18]使用了一种距离度量法来匹配规则。具体方法为:
设被预测对象为,条件属性值为{1(),2(),…,y()},规则集中规则的条件属性值为{1(),2(),…,y()}。统计规则集中所有规则的条件属性值与的条件属性值不匹配的数目,将该数目最小的规则取出,构成候选规则集。若候选规则集中只有1条规则,以该规则为匹配规则,否则按式(5)度量各候选规则与的距离,即相似程度,以距离最近的规则为匹配规则。
式中,ymax和ymin分别是y最大值和最小值;为决策规则中条件属性的个数。
确定规则后,将的决策属性值划归该规则的决策类别,即由规则的结论确定的寿命预测结果。
3.3 数据处理与应用实例
3.3.1 继电器寿命决策表的构建与约简
从第1节所述12组继电器寿命数据中,随机选用其中的9组(用1~9表示)建立寿命决策规则,剩下的3组(用10~12表示)用来验证规则的有效性。提取1~9的试验最终寿命数据及其生命中最初10万次内的性能参数数据,并对生命中最初10万次内的性能参数数据做平均值统计,得到9个试品的性态参数与寿命信息表,见表2。
表2 继电器性能参数与寿命信息表
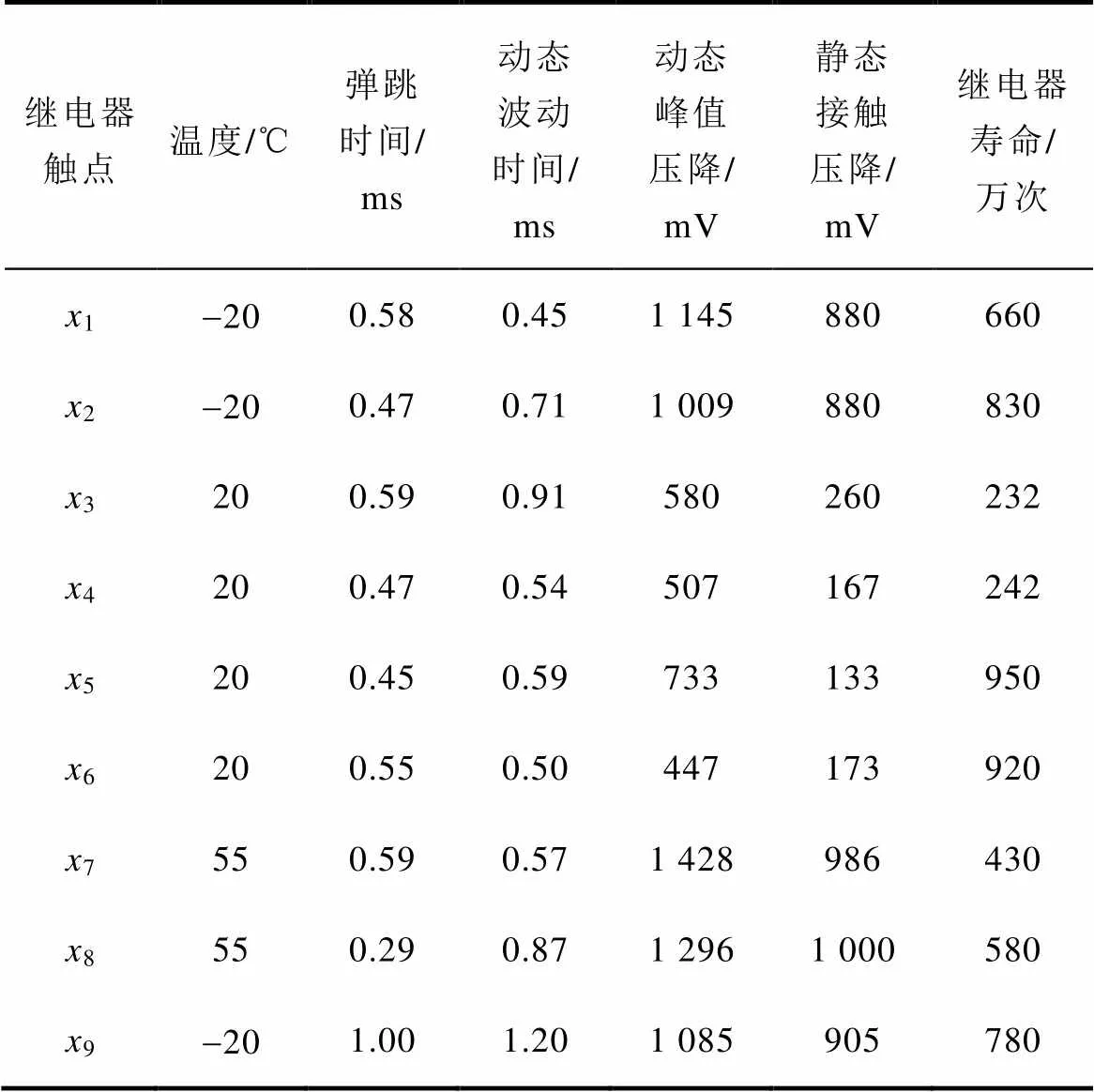
Tab.2 Information table of parameter performance and life of relays
其中,决策属性(继电器寿命)的离散可根据产品的实际筛选需求进行,本实例中将其划分为1、2、3三个等级(也可以认为是三个模糊语言值,例如“小、中、大”),条件属性则根据数据特点采用经验法进行离散。具体离散方法如下:
对于环境温度,“1”表示其值属于[L, 0℃这一区间;类似地,“2、3”分别表示其值属于[0,50℃和[50,H]℃区间。其中,L、H分别为继电器可正常工作的环境温度下限、上限,这两个值一般由产品生产厂家提供,也可以通过实验获得。
对于弹跳时间,“1、2、3”分别表示其值属于[0,0.5ms、[0.5,0.8ms、[0.8,+∞ms区间。
对于动态波动时间,“1、2、3”分别表示其值属于[0,0.6ms、[0.6,1.0ms、[1.0,+∞ms区间。
对于动态峰值压降,“1、2、3”分别表示其值属于[0,600mV、[600,1 000mV、[1 000,+∞mV区间。
对于静态接触压降,“1、2、3”分别表示其值属于[0,400mV、[400,800mV、[800,+∞]mV区间。
对于继电器的寿命,“1、2、3”分别表示其值属于[0,600万次、[600,900万次、[900,+∞]万次 区间。
数据处理过程如下:
(1)继电器寿命决策表的建立。按照上述离散规则,对表2进行离散操作,并按条件属性和决策属性分类,其中1,2,…,5均为条件属性,分别表示环境温度、弹跳时间、动态波动时间、动态峰值压降、静态接触压降;为决策属性,表示工作寿命。如此便得到继电器的寿命决策表,见表3。
表3 继电器寿命决策表
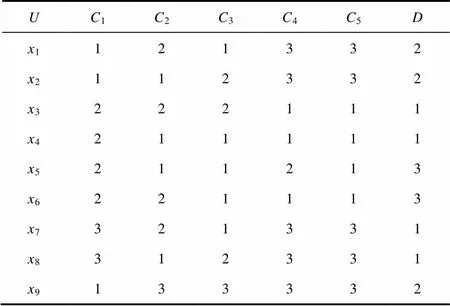
Tab.3 Life decision table of relays
(2)继电器寿命决策表的约简。求取与继电器寿命有关的最简属性集,可基于粗糙集理论中的属性约简来完成。以下是对表3所示的继电器寿命决策表的属性约简过程,即条件属性“”对决策属性“继电器寿命”的约简。具体约简过程如下:
记和之间依赖度为,=说明属性集={温度, 弹跳时间,动态波动时间,动态峰值压降,静态接触压降}对继电器寿命的分类是充分集合,完全依赖于。
由以上计算可知,1~4分别相对于不可单独约简,5相对于可单独约简。因此,得到的核为={环境温度、弹跳时间、动态波动时间、动态峰值压降},这也是约简所得的最简属性集。
3.3.2 继电器寿命决策规则的获取
通过前述的属性约简及求核,可以得到简化的寿命决策表见表4。
表4 继电器寿命决策规则表
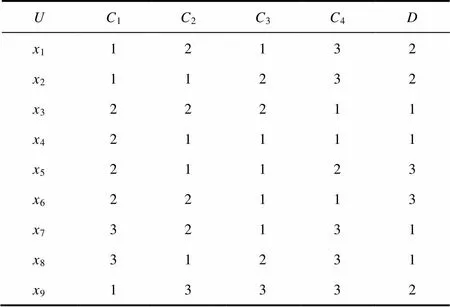
Tab.4 Life decision rules table of relays
根据表4可得到如下一组决策规则:
Rule1:(1,1)∧(2,2)∧(3,1)∧(3,3)→(,2)
Rule2:(1,1)∧(2,1)∧(3,2)∧(3,3)→(,2)
Rule3:(1,2)∧(2,2)∧(3,2)∧(3,1)→(,1)
Rule4:(1,2)∧(2,1)∧(3,1)∧(3,1)→(,1)
Rule5:(1,2)∧(2,1)∧(3,1)∧(3,2)→(,3)
Rule6:(1,2)∧(2,2)∧(3,1)∧(3,1)→(,3)
Rule7:(1,3)∧(2,2)∧(3,1)∧(3,3)→(,1)
Rule8:(1,3)∧(2,1)∧(3,2)∧(3,3)→(,1)
Rule9:(1,1)∧(2,3)∧(3,3)∧(3,3)→(,2)
根据式(4)求得本实例中每条决策规则的可信度均为1,说明所得决策规则都是确定性规则。实际应用中可将1作为决策规则的初始可信度,在出现与决策规则相冲突(条件属性值相同,决策属性值不同)的实例后,可根据冲突的频率、基于概率论方法调整规则可信度(通常为小于1的正实数)。当规则可信度下降到一定阈值(比如0.5),此条规则就不适宜再直接使用,此时需要重新选择样本进行规则提取,从而实现对规则组的修正、补充。
3.3.3 寿命预测及决策规则有效性分析
根据寿命决策规则对继电器1012进行寿命预测,首先提取1012的生命初期性能参数数据,并做平均值统计,再利用前述的离散化方法进行离散分类,然后匹配决策规则进行寿命预测。被预测继电器的生命初期性能参数信息见表5。
表5 待预测继电器的工作寿命与性能参数
Tab.5 The working life and performance parameters of the predicted relays

继电器编号数据温度/℃弹跳时间/ms动态波动时间/ms动态峰值压降/mV工作寿命/万次 x10实际值-200.530.481 035750 离散值12132 x11实际值550.590.491 218540 离散值32131 x12实际值550.401.001 230370 离散值31331
对照3.3.2建立的寿命决策规则,继电器10匹配第一条规则,并且可信度为1,对应预测寿命等级为2,与实际寿命结果一致(10实际寿命为750万次);继电器11匹配第七条规则,并且可信度为1,对应预测寿命等级为1,与实际寿命结果一致(11实际寿命为540万次);然而,决策规则中没有与继电器12相匹配的规则,这里参照文献[18]中的距离度量法进行规则匹配。根据上述方法,发现继电器12的候选规则只有一条规则,即Rule8,故以该规则为匹配规则。Rule8对应的寿命等级为1,所以可推测继电器12的寿命等级为1。这一推测与继电器实际寿命370万次一致。
4 结论
通过分析继电器的寿命试验数据,发现继电器个体的寿命与其生命初期的性态有着某种关系。本文基于这一发现,提出了一种基于粗糙集理论的继电器寿命预测方法,预测的精细程度取决于寿命的离散分类等级数。离散分类等级数越高,每一等级所表征的区间越窄,预测结果也就越精细。当仅需判断继电器个体是否能达到期望的寿命值时,寿命的离散分类等级数为2即可,分别代表“达到”和“未达到”,这种简单易行的方法为以寿命为指标的产品筛选带来极大便利。
与当前常用的继电器产品寿命预测和产品筛选方法相比,本文方法的特点体现在:①简单、快捷、运算量小、所依赖的信息量少,仅需测出继电器个体在生命初期的性能参数数据。②寿命预测的对象为继电器产品个体而非批产品,因此非常适用于以工作寿命为指标的继电器产品等级划分与筛选。③由于仅需对继电器在其生命初期的性能参数进行测试,故在筛选过程中不会过多压缩其有效服役期,同时也大大降低了产品筛选的成本。
该方法亦可推广应用于其他产品的寿命预测与产品筛选,只要该产品的寿命与其生命初期特征具有相关性。
参考文献
[1] 张又衡. 车辆继电器寿命综合实验台[D]. 长春: 吉林大学, 2007.
[2] 张菲菲, 李志刚. 基于BP神经网络的继电器剩余寿命预测[J]. 低压电器, 2012(1): 11-14.Zhang Feifei, Li Zhigang. Remaining lifetime prediction of relay based on BP neural network[J].Low Voltage Apparatus, 2012(1): 11-14.
[3] 李华, 孙东旺, 贺鹏举, 等. 基于超程时间回归模型的继电器寿命预测方法[J]. 电工技术学报, 2013, 28(S2): 414-417. Li Hua, Sun Dongwang, He Pengju, et al. The method of relay life prediction based on the regression model of super-path time[J]. Transactions of China Electrotech- nical Society, 2013, 28(S2): 414-417.
[4] Ye Xuerong, Yu Qiong, Zhai Guofu. Reliability assessment for electromagnetic relay based on time parameters degradation[C]//2010 11th International Conference on Electronic Packaging Technology & High Density Packaging, Xi’an, 2010: 1269-1272.
[5] Yu Qiong, Qi Ming, Wang Shujuan, et al. Research on life prediction based on wavelet transform and ARMA model for space relay[C]//4th IEEE Conference on Industrial Electronics and Applications, Xi’an, 2009: 1275-1280.
[6] 任立. 航天继电器可靠性寿命试验分析系统的研究[D]. 哈尔滨: 哈尔滨工业大学, 2009.
[7] 王淑娟, 余琼, 翟国富. 电磁继电器接触失效机理判别方法[J]. 电工技术学报, 2010, 25(8): 38-44.Wang Shujuan, Yu Qiong, Zhai Guofu. Discrimination method of contact failure mechanisms for electro- magnetic apparatus[J]. Transactions of China Electro- technical Society, 2010, 25(8): 38-44.
[8] 冯兴杰, 潘文欣, 卢楠. 基于小波包的RBF神经网络网络流量混沌预测[J]. 计算机工程与设计, 2012, 33(5): 1681-1686.Feng Xingjie, Pan Wenxin, Lu nan. Research on chaotic prediction method of network traffic based on wavelet packet[J]. Computer Engineering and Design, 2012, 33(5): 1681-1686.
[9] Liu Guilong. Rough set theory based on two universal sets and its applications[J]. Knowledge-Based Systems, 2010, 23(2): 110-115.
[10] 高爽, 冬雷, 高阳, 等. 基于粗糙集理论的中长期风速预测[J].中国电机工程学报, 2012, 32(1):32-37.Gao Shuang, Dong Lei, Gao Yang, et al. Mid-long term wind speed prediction based on rough set theory[J]. Proceedings of the CSEE, 2012, 32(1): 32-37.
[11] Yanyan Yang, Degang Chen, Ze Dong. Novel algo- rithms of attribute reduction with variable precision rough set model[J]. Neurocomputing, 2014, 139(2): 336-344.
[12] Kai Zheng, Jie Hu, Zhenfei Zhan. An enhancement for heuristic attribute reduction algorithm in rough set[J]. Expert Systems with Applications, 2014, 41(15): 6748-6754.
[13] 高晓红. 基于分类质量的决策系统属性约简新算法[J]. 计算机与现代化, 2010(1): 19-22. Gao Xiaohong. Novel attribute reduction algorithm of decision system based on classification quality[J]. Computer and Modernization, 2010(1): 19-22.
[14] Jing Tian, Quan Wang, Yu Bing. A rough set algo- rithm for attribute reduction via mutual information and conditional entropy[C]//Fuzzy Systems and Know- ledge Discovery(FSKD), Shenyang, 2013: 567-571.
[15] Wang Yun, Wu Zhiqiang. Generating algorithm of approximate decision rules and its application[C]// Granular Computing(GrC), San Jose, CA, 2010: 830- 833.
[16] Qiong Wu, Xin Pan. A novel remote sensing classify- cation rule extraction method based on discrete rough set[C]//Fuzzy Systems and Knowledge Discovery (FSKD), Shanghai, 2011: 330-334.
[17] 杨传振, 朱玉全, 陈耿. 一种基于粗糙集属性约简的多分类器集成方法[J]. 计算机应用研究, 2012, 29(5): 1648-1650. Yang Chuanzhen, Zhu Yuquan, Chen Geng. New classifier ensemble method based on rough set attributereduction[J]. Application Research of Computers, 2012, 29(5): 1648-1650.
[18] 龙丹丽, 黎静华, 韦化. 粗糙集法解多环境因素影响的母线负荷预测问题[J]. 电网技术, 2013, 37(5): 1335-1340. Long Danli, Li Jinghua, Wei Hua. Solution of multi environmental factor-influenced bus load forecasting by rough set method[J]. Power System Technology, 2012, 37(5): 1335-1340.
The Life Prediction Method of Relay Based on Rough Set Theory and Relay’s Initial Life Information
(Province-Ministry Joint Key Laboratory of Electromagnetic Field and Electrical Apparatus Reliability Hebei University of Technology Tianjin 300130 China)
Working life is an important feature of product reliability. However the productscreening method using life as the sole index hasn’t been thoroughly studied for long life products such as relays. After the life test data of relays was analyzed,a fact was foundrecently that there are some relations between relay’s initial working state and its working life, i.e., better performance of the initial state, longer life expectancy of the individual relay, and vice versa. Based on the fact, a method of the individual relay’s life predicting and screening was presented. Firstly, obtained the initial state performance parameters values and life values of the sample relays through life test. Secondly, extracted a set ofparameters associated with life based on the method of attribute reduction from the rough set theory, then established a set of life decision rules based on the extracted parameters. After that, for any one of the relay whose model same as the samples, its life could be predicted only according to its initial state information and the rules, then the screening using life as the sole index could be achieved. At last, the availability of the above method was proved by a practical example of relay.
Relay, initial state information, life prediction, product screening, rough set theory
TM581.3
李玲玲 女,1968年生,博士,教授,博士生导师,研究方向为电器可靠性、电力系统及其自动化。
E-mail: lilingling@hebut.edu.cn
李志刚 男,1958年生,博士,教授,博士生导师,研究方向为电子电器、电器可靠性及其检测技术。
E-mail: zgli@hebut.edu.cn(通信作者)
2014-07-28 改稿日期 2014-09-19
国家自然科学基金(61072100、51377044),河北省自然科学基金(E2014202230)和河北省高校创新团队领军人才培育计划(LJRC003)资助项目。

