拉格朗日微分中值定理中间点集的稳定性

何基好

(贵州大学理学院，贵州贵阳　550025)

拉格朗日微分中值定理中间点集的稳定性

何基好*

(贵州大学理学院，贵州贵阳550025)

先给出拉格朗日微分中值定理本质中间点的定义，再研究其定理中间点集的稳定性，最后得到闭区间[a，b]上大多数一阶导函数都连续函数的中间点集在Baire分类意义下均为稳定的，并给出其中间点集为本质连通区的一个充分条件。

拉格朗日微分中值定理；一阶导函数都连续的函数；中间点

拉格朗日微分中值定理[1]:设函数f(x)在闭区间[a，b]上连续，在开区间(a，b)内可导，则至少∃ ξ∈[a，b]，使得

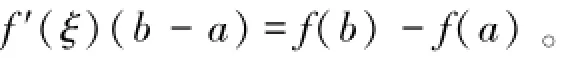
该定理是高等数学微分学中一个非常重要的定理，有着广泛的应用。该定理中点ξ称为函数f(x)在闭区间[a，b]上的中间值点，简称f的中间点。文献[2]、[3]等都研究了f的中间点的渐近性。对于闭区间[a，b]上的一阶导函数都连续的函数f(x)，这样的中间点是不唯一的。本文研究其函数f(x)的中间点集的稳定性，即当函数f(x)产生微小扰动时，f(x)的中间点集是不是也产生微小扰动，有例子表明该结论不一定成立。为此，先给出拉格朗日微分中值定理本质中间点的定义，再研究其定理中间点集的稳定性，最后得到闭区间[a，b]上大多数一阶导函数都连续函数的中间点集在Baire分类意义下均为稳定的，并给出其中间点集为本质连通区的一个充分条件。

1　预备知识

设X和Y是两个Hausdorff拓扑空间，F:X→P0(Y)是一个集值映射，即∀x∈X，F(x)是Y中的非空集合。

定义11)如果对Y中的任意开集G，G⊃F(x)，存在x的开邻域O(x)，使得∀x′∈O(x)，有G⊃F(x′)，则称集值映射F在x是上半连续的。

2)如果对Y中的任意开集G，G∩F(x)≠Ø，存在x的开邻域O(x)，使得∀x′∈O(x)，有G∩F(x′)≠Ø，则称集值映射F在x是下半连续的。

3)如果集值映射F在x既上半连续又下半连续，则称F在x是连续的。

4)如果∀x∈X，集值映射F在x是连续的(或上半连续的，或下半连续的)，则称F在X上是连续的(或上半连续的，或下半连续的)。

5)如果∀x∈X，F(x)是紧集，且集值映射F 在x处上半连续的，则称F是X上的一个上半连续紧值映射，简称usco映射。

C1[a，b]表示定义在闭区间[a，b]上的所有一阶导函数都连续的函数构成的集合，∀f，g∈C1[a，b]，定义度量ρ和范数｜｜·｜如下:

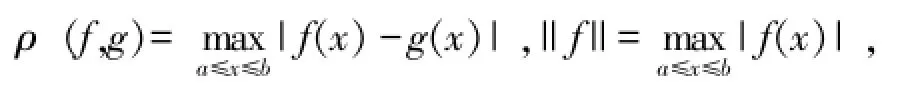
易见C1[a，b]是Banach空间[3]。

设X⊂R＝(-∞，+∞)是非空有界闭区间，P0(X)表示X的所有非空子集构成的集合，∀A，B ∈P0(X)，定义

为A和B之间的Hausdorff距离。特别，当A＝[a，b]，B＝[c，d]时，有h(A，B)＝max{｜c-a｜，｜d-b｜}。

以下引理1为Fort定理，参观文献[4-5]。引理1设X是一个Baire空间，Y是一个度量空间，F:X→P0(Y)是一个usco映射，则存在X中一个稠密剩余集Q，使∀x∈Q，F在x是下半连续，从而是连续的。

2　结论

∀f∈ C1[a，b]，记 E(f)＝{ξ∈ [a，b]: f′(ξ)(b-a)＝f(b)-f(a)}为函数f的中间点集，则E定义一个由C1[a，b]到[a，b]的集值映射，映射E具有以下性质:

引理2映射E是一个usco映射。

证明由于闭区间[a，b]是紧的，要证映射E是紧值的，只需证∀f∈C1[a，b]，E(f)是闭集。

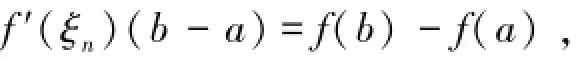
又因为f′∈C1[a，b]，从而f′(ξ)(b-a)＝f(b)-f(a)，即ξ∈E(f)，故E(f)是闭集。由于闭区间[a，b]是紧的，要证映射E是上半连续的，只需证其图像

综上所述，映射E是一个usco映射。

定义21)∀f∈C1[a，b]，若对ξ的任意开邻域O(ξ)⊂[a，b]，∃δ>0，使得对任意满足ρ(f，g)<δ的g∈C1[a，b]，都有O(ξ)∩E(g) ≠Ø，则称ξ∈E(f)为f的本质中间点。

2)∀f∈C1[a，b]，若∀ξ∈E(f)，ξ都是f的本质中间点，则称f是本质的。

3)∀f∈C1[a，b]，设Eα(f)是E(f)的非空闭子集，若对[a，b]中的任何开集O，Eα(f)⊂O，存在δ>0，使得对任意满足ρ(f，g)<δ的g∈ C1[a，b]，都有O(ξ)∩E(g)≠Ø，则称Eα(f) 是E(f)的本质连通区。

4)∀f∈C1[a，b]，如果G在f是连续的，则称f的中间点集E(f)是稳定的。

由定义1及定义2得到定理1。

定理1映射E在f∈C1[a，b]处下半连续的充要条件为f是本质的。

由引理1、引理2和定理1可得到定理2。

定理2存在C1[a，b]中一个稠密剩余集Q，使得对∀f∈Q⊂C1[a，b]，E在f处是下半连续的，从而f∈Q是本质的，E在f处是连续的，即E(f)是稳定的。

由定理2易知，仍然∃ f∈C1[a，b]，使得映射E在f处是不连续的，即E(f)是不稳定的。

例1设[a，b]＝[0，1]，f(t)＝t，t∈[0，1]，则E(f)＝[0，1]，下面说明映射E在f处是不连续的，即E(f)是不稳定的。

此例说明，当C1[a，b]中的一阶导函数都连续的函数f产生微小扰动时，但f的中间点集E(f)会产生较大扰动，即中间点集不稳定，虽然不能得到E(f)是稳定的，但可以得到E(f)为本质连区的一个充分条件。

定理3设f∈ C1[a，b]，若E(f)＝[α，β]⊂[a，b]，则E(f)是本质连通区。

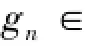
推论1设f∈C1[a，b]，若E(f)为单点集{x0}，则x0是f的本质中间点，此时映射E在f处是连续的。

注1设f∈C1[a，b]，若E(f)不是单点集，则f可能没有本质中间点。

例2设[a，b]＝[0，1]，f(t)≡0，t∈[0，1]，则E(f)＝[0，1]不是单点集，下面说明f没有本质中间点。

事实上，∀x0∈[0，1]，若x0∈(0，1)，取充分小的δ>0，使得(x0-3δ，x0+δ)⊂[0，1]。

∀ε>0，令

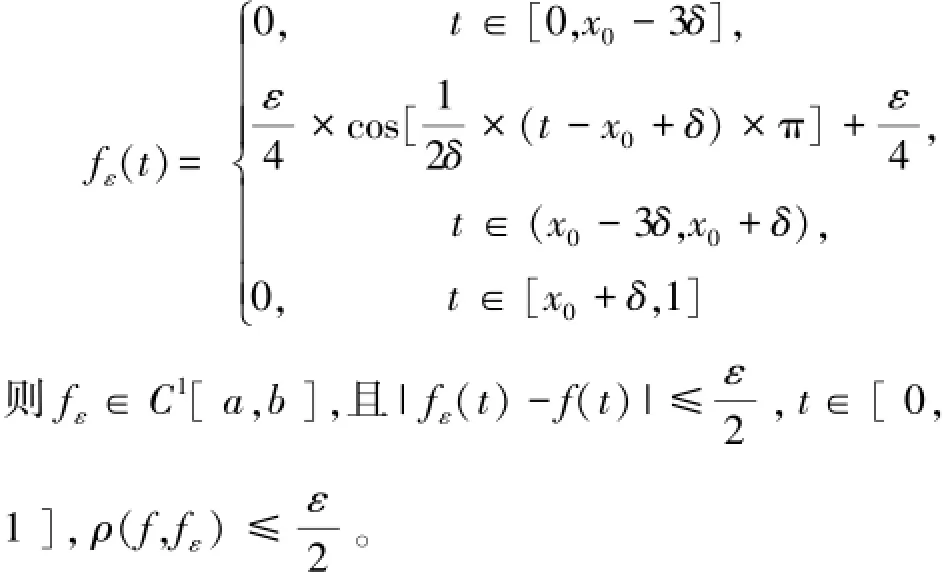
所以E(fε)＝[0，x0-3δ]∪{x0-δ}∪[x0+δ，1]，从而E(fε)∩(x0-δ，x0+δ)＝Ø，故x0不是f的本质中间点，即f没有本质中间点。

同理可推x0＝0与x0＝1均不是f的本质中间点，即f没有本质中间点。

[1]马知恩，王绵森.高等数学简明教程[M].北京:高等教育出版社，2005.

[2]张新元，王骁力.一类函数第一积分中值定理中值点的渐近性[J].数学的实践与认识，2011，41(4):228-233.

[3]江泽坚，孙善利.泛函分析[M].北京:高等教育出版社，1998.

[4]Fort M K.Points of continuity of semicontinuous functions[J].Publ. Math.Debrecen，1951(2):100-102.

[5]俞建.博弈论与非线性分析续论[M].北京:科学出版社，2011.

[6]罗群.积分第一中值定理中值点集稳定性的注记[J].肇庆学院学报，2011，32(5):5-7.

(责任编辑:曾晶)

The Stability of Intermediate Value Point Set of Lagrange Mean Value Theorem for Differential

HE Jihao*
(College of Science，Guizhou University，Guiyang 550025，China)

The concept of essential intermediate value point in lagrange mean value theorem for differential is introduced，and the stability of the intermediate value point set is discussed.It proves that the intermediate value point set of most the first-order derivative and continuous function(in the Baire category sense)is stable；and a sufficient condition for the existence of one essential component in the intermediate value point set of the first-order derivative and continuous function is obtain.

lagrange mean value theorem for differential；the first-order derivative and continuous function；intermediate value point

O172.2

A

1000-5269(2016)01-0013-03DOI:10.15958/j.cnki.gdxbzrb.2016.01.04

2015-06-18

贵州省科学技术基金(黔科合J字[2014]2058号)

何基好(1976-)，男，讲师，硕士，研究方向:基础数学，Email:jhhe76＠sina.com.

何基好，Email:jhhe76＠sina.com.