具有部分缺失数据的两个Pareto分布总体参数的估计与检验

龙　兵，王秋节，习长新

(荆楚理工学院数理学院，湖北荆门　448000)

具有部分缺失数据的两个Pareto分布总体参数的估计与检验

龙兵*，王秋节，习长新

(荆楚理工学院数理学院，湖北荆门448000)

在数据缺失样本下研究了Pareto分布的参数估计和假设检验。在门限参数已知的条件下给出了形状参数的极大似然估计，证明了估计量的相合性和渐近正态性，并给出了两总体形状参数之差的置信区间和假设检验，最后通过蒙特卡洛随机模拟说明了估计的优良性。

Pareto分布；缺失数据；极大似然估计；假设检验

在利用统计方法处理试验数据时，经常会遇到数据缺失的情况，如在进行寿命试验时，由于试验数据不易观测或者受访者不愿意透露，如何根据缺失数据进行统计推断是统计分析中的一个重要问题。文献[1-4]分别讨论了几何分布总体、幂分布总体、对数正态分布总体、及瑞利分布总体的参数估计与假设检验问题；文献[5]讨论了在缺失数据样本下两个二项分布总体的参数估计问题。文献[6-7]讨论了在定数截尾缺失数据样本下，两个指数分布、Rayleigh分布总体的参数及假设检验问题；文献[8]讨论了在定时截尾下两个几何总体参数的估计。本文进一步讨论在数据缺失样本下pareto分布的参数估计和假设检验，在门限参数已知的条件下给出了形状参数的极大似然估计，证明了估计量的相合性和渐近正态性，并给出了两总体形状参数之差的置信区间和假设检验。

1　极大似然估计及其渐近性质

设样本观测数据分别来自两个Pareto分布总体，其密度函数为:

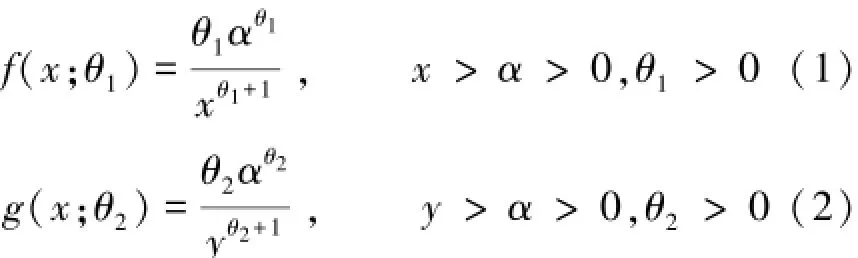
其中θ1，θ2称为形状参数，α称为门限参数，在本文中假设两个总体的门限参数已知。

假设对上述两个Pareto分布进行n次独立观测，每次样本观测值以概率1-P被丢失，以概率P被观测。用(Xi，δi)，i＝1，2，…，n表示来在第一个总体的观测值，其中Xi表示来自第一个Pareto分布总体(1)的第i个样本观测值，并且如果第i个观测值丢失，记为δi＝0，否则记为δi＝1。第二个Pareto分布总体的样本观测值为(Yi，ηi)，i＝1，2，…，n。其中Yi表示来自第二个Pareto分布总体(2)的第i个样本观测值，并且如果第i个观测值丢失，记为ηi＝0，否则记为ηi＝1。

下面用极大似然估计方法对未知参数θ1进行估计，基于上述样本观测值(Xi，δi)，i＝1，2，…，n，可得到似然函数为:

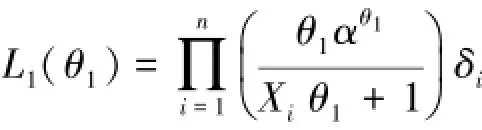
对数似然函数为:

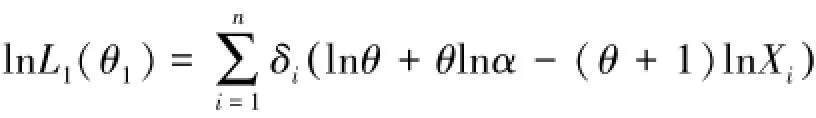
对参数θ1求导:

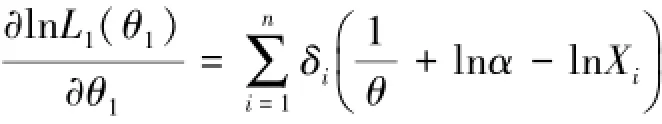
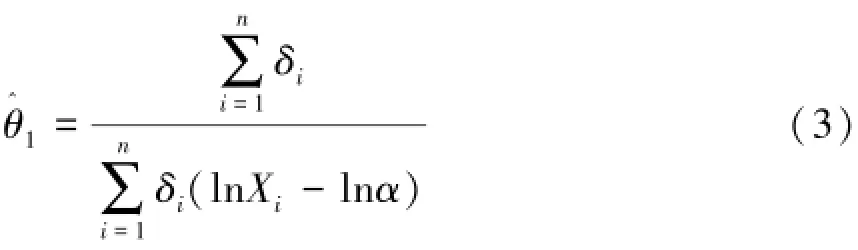
同理，基于样本观测值(Yi，ηi)，i＝1，2，…，n，也可以得到θ2的极大似然估计为:

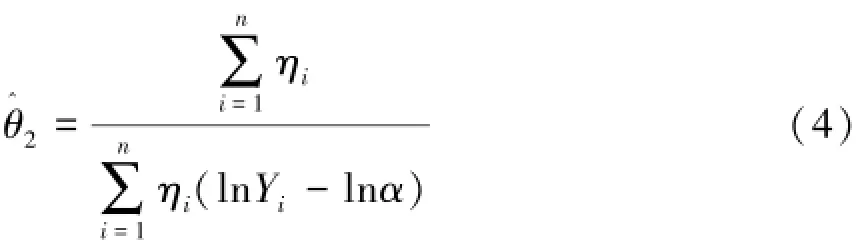
由θ1的极大似然估计可得到如下定理:

定理1若(Xi，δi)，i＝1，2，…，n，是来自Pareto分布总体(1)的样本观测值，则有

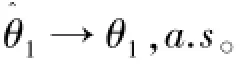
证明:由于{δi(lnXi-lnα)，1≤i≤n}为独立同分布随机变量，因此由强大数定律可得到

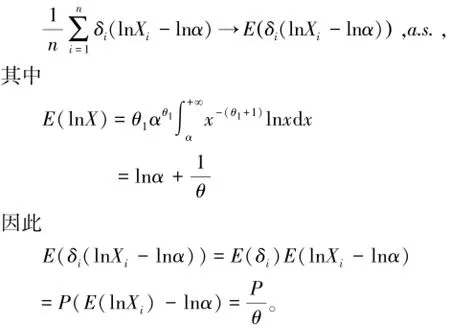
同样由强大数定律得

引理1[9]，设

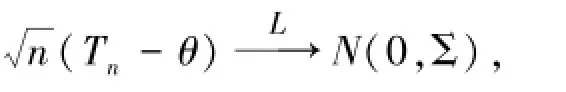
其中Σ＝(σij)k×k。又设g(t1，…，tn)对各ti有连续偏导数，则当n→∞时，有

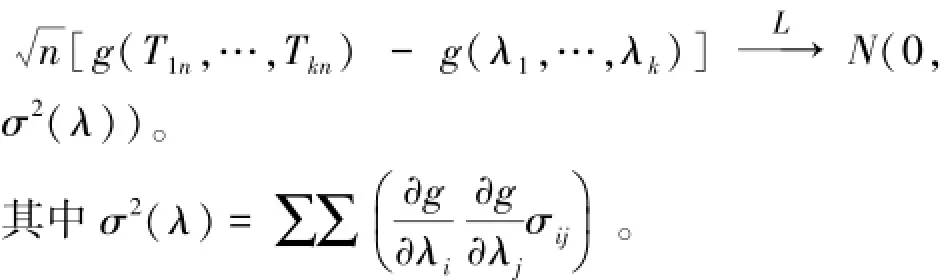
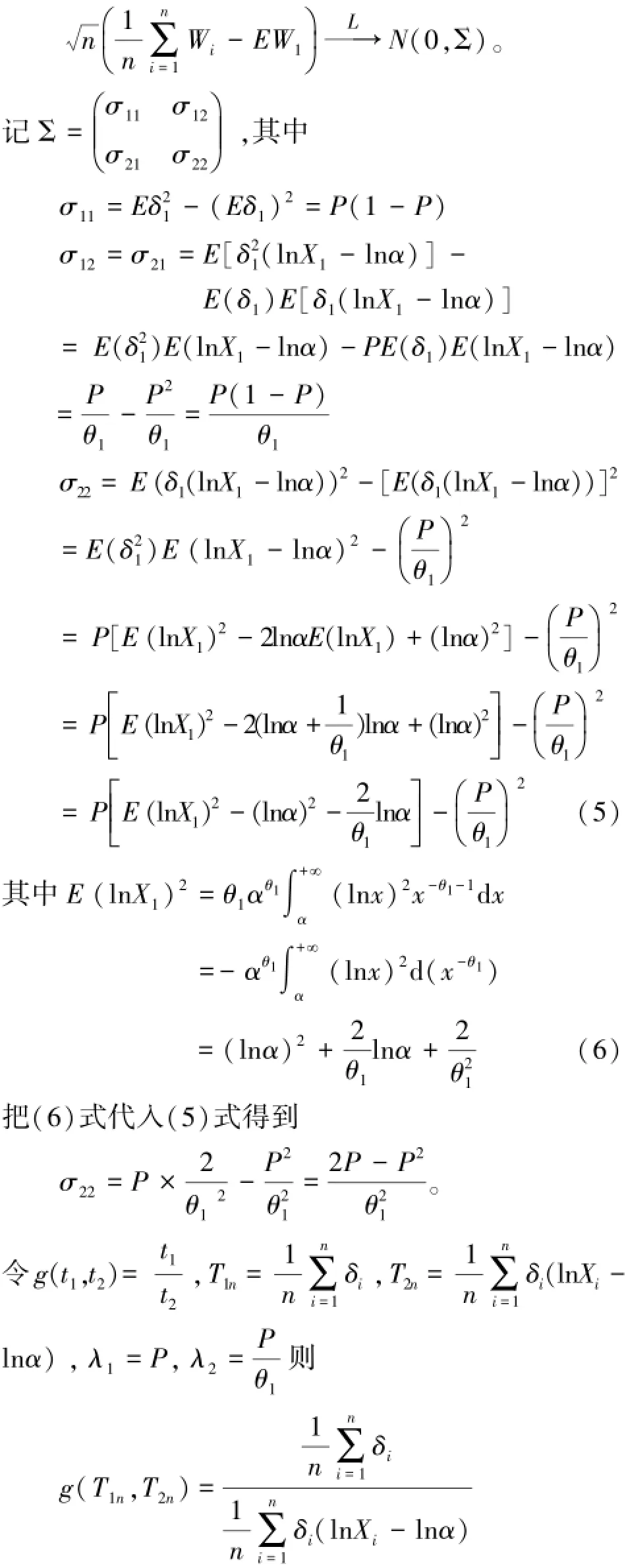
2　两总体参数之差的区间估计及参数之比的假设检验

在实际中，人们常常要比较两个参数的大小，

这样就可以归结到参数之差的置信区间问题。对于本文中讨论的问题可得到如下定理。

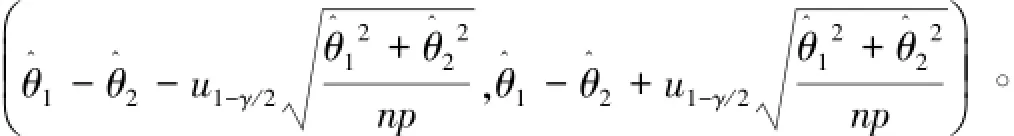
其中uγ为标准正态分布的γ下分位数。

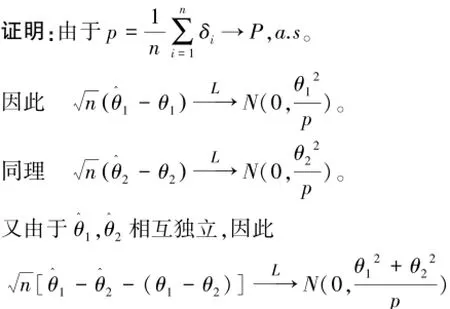
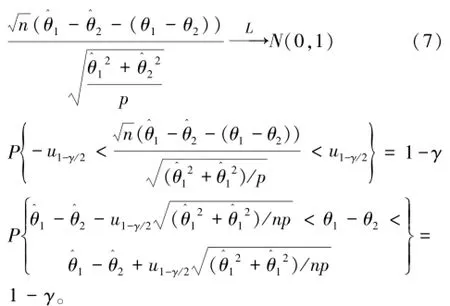
因此θ1-θ2的置信水平为1-γ的近似置信区间为

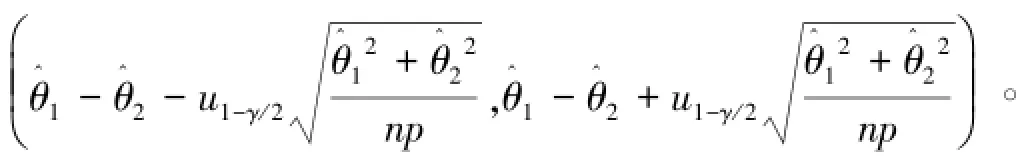
(I)对于假设检验问题

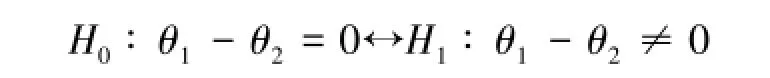
当H0成立时，

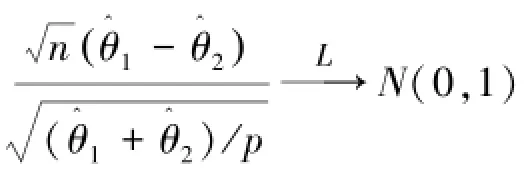
对于给定的显著性水平γ(0<γ<1)，检验的拒绝域为

同理可得，对于给定的显著性水平γ(0<γ<1)，检验的拒绝域为

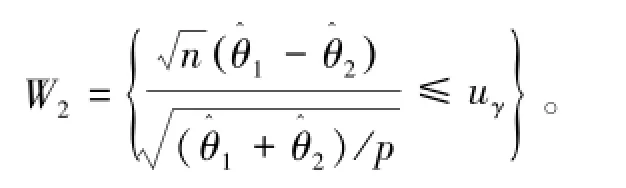
(III)对于假设检验问题

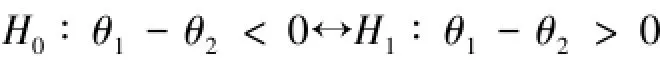
同理可得，对于给定的显著性水平γ(0<γ<1)，检验的拒绝域为

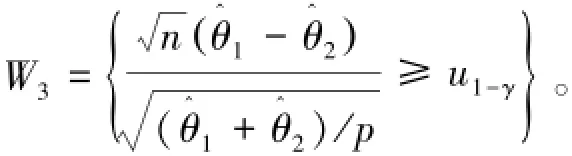
3　随机模拟

当α＝2时，在参数θ1，θ2取不同的真值的情况下，在计算机上通过随机模拟的方法，分别产生两个服从Pareto分布(1)(2)的样本，且样本容量n＝100。取缺失概率1-P＝0.1，置信水平1-γ＝0.95，利用上述两个样本可以得到参数θ1，θ2的估计，以上过程重复1000次，可以得到参数估计的均值、均方误差及置信区间的上下限均值，模拟结果列于表1中。

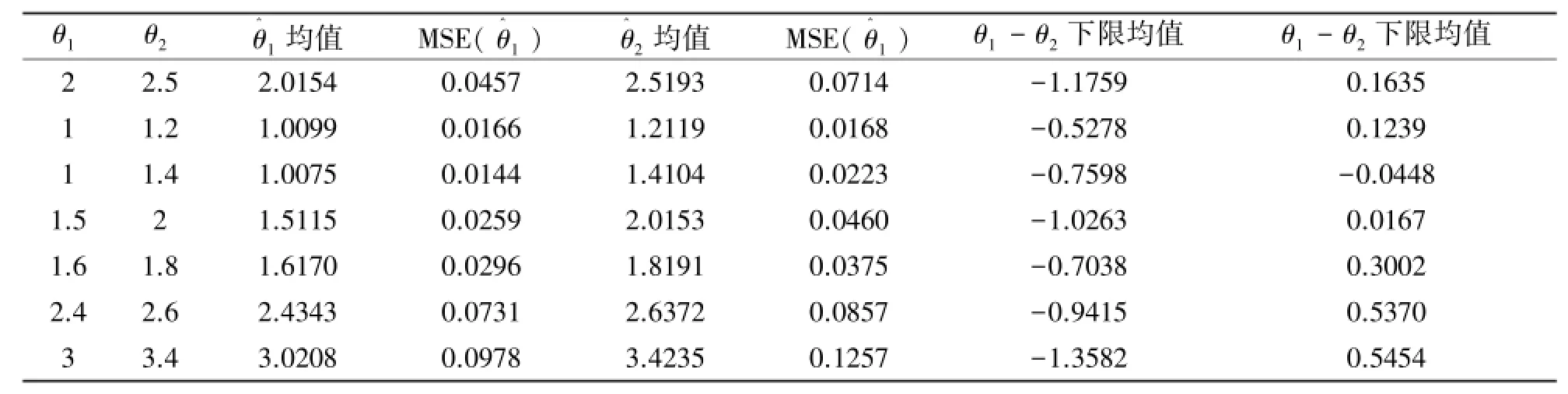
表1　参数估计的均值、均方误差及置信区间的上下限均值

从上表中的数据可以看到，对形状参数的估计都很接近参数真值，并且均方误差较小。

θ1-θ2的真值介于下限均值与上限均值之间。

[1]赵志文，宋立新，刘银萍.具有部分缺失数据的两个几何分布总体参数的估计与检验[J].统计与决策，2010，5:22-23.

[2]赵志文，刘银萍.具有部分缺失数据的两个幂分布总体参数的估计与检验[J].吉林师范大学学报(自然科学版)，2008，29 (3):103-104.

[3]赵志文，赖民，宋立新，等.具有部分缺失数据的两个对数正态分布总体参数的估计与检验[J].统计与决策，2009，20:7-9.

[4]赵志文，付志慧.具有部分缺失数据的两个瑞利分布总体参数的估计与检验[J].北华大学学报(自然科学版)，2008，9(3): 202-204.

[5]李洪毅，欧祖军.具有部分缺失数据的两个二项分布的估计[J].甘肃联合大学学报，2009，23(3):8-9.

[6]赵志文，王思洋，王瑞庭，等.定时截尾下具有部分缺失数据两个指数总体参数的估计与检验[J].吉林大学学报(理学版)，2009，47(1):26-30.

[7]赵志文，M.S.Abdalroof，盛丹姝.定时截尾下具有缺失数据两个Rayleigh分布总体参数的估计与检验[J].吉林大学学报(理学版)，2013，51(6):1090-1094.

[8]孙坤，任亮.定时截尾下具有缺失数据的两个几何总体参数的估计[J].统计与决策，2012，7:38-41.

[9]茆诗松，王静龙，濮晓龙.高等数理统计学[M].北京:高等教育出版社，2013.

(责任编辑:曾晶)

Parameter Estimation and Hypothesis Testing of Two Pareto Distribution with Missing Data

LONG Bing*，WANG Qiujie，XI Changxin
(College of Mathematics and Physics，Jingchu University of Technology，Jingmen 448000，China)

Parameter estimations and hypothesis were studied on Pareto distribution under missing data samples. Maximum likelihood estimation of the shape parameters was discussed.The consistency and asymptotic normality of the estimators were proved.Moreover，the difference of the confidence interval and hypothesis test between the two general shape parameters was given.Finally，Monte Carlo simulation was used to illustrate the excellent performance of the estimator.

Pareto distribution；missing data；maximum likelihood estimation；hypothesis testing

O212.7

A

1000-5269(2016)01-0009-04DOI:10.15958/j.cnki.gdxbzrb.2016.01.03

2015-12-02

荆楚理工学院院级科研项目(ZR201504)

龙兵(1973-)，男，副教授，研究方向:数理统计，Email:qh-longbing＠163.com.

龙兵，Email:qh-longbing＠163.com.