气隙静态偏心故障下汽轮发电机励磁绕组受载及其力学响应分析*

蒋宏春，　伍世良，　何玉灵，　仲　昊，　唐贵基

(1. 华北电力大学 机械工程系，河北 保定　071003；2. 柳州发电有限责任公司，广西 柳州　545000)



气隙静态偏心故障下汽轮发电机励磁绕组受载及其力学响应分析*

蒋宏春1，伍世良2，何玉灵1，仲昊1，唐贵基1

(1. 华北电力大学 机械工程系，河北 保定071003；2. 柳州发电有限责任公司，广西 柳州545000)

以QFSN-600-2YHG汽轮发电机为研究对象，分析了转子励磁绕组在气隙静态偏心下的变形、应力及应变响应。首先对转子绕组结构及其受载情况进行了分析；然后在SolidWorks中建立了绕组的三维模型，并将其导入至Ansys中，通过加载偏心后的电磁力载荷计算得到了绕组的力学响应数据。结果表明转子绕组的变形、应变和应力具有空间对称性，转子绕组变形量从靠近大齿的绕组向远离大齿的绕组逐渐减小且存在轴向滑移；转角部分应力和应变最大，直线部分的应变和应力最小；1、16、2、15、8号绕组的转角和圆弧部分较为危险。这些结论对转子结构优化及绕组固定设计具有参考价值。

汽轮发电机； 励磁绕组； 气隙静态偏心； 力学响应

0　引　言

大型汽轮发电机的故障有多种，其中气隙静态偏心是较为常见的一种。气隙静态偏心会使得气隙分布不对称并导致磁场畸变，从而加剧定转子振动，引发绕组绝缘磨损和移位变形。因此，研究气隙静态偏心故障下转子绕组的力学响应具有积极意义。

有关气隙静态偏心故障的文献多集中于偏心磁场的研究和故障下电气特性或定转子振动特性的分析。文献[1]针对转子偏心时电磁场的复杂性，建立了精确的电磁场分析模型；文献[2]针对电机回转偏心检测的问题,提出了基于电流信息与位置信息的电机偏心特征辨识方法；文献[3- 4]分别分析了偏心故障下定子和转子的振动特性。这些分析结论对于偏心故障的诊断有着重要的参考价值。

关于绕组的力学响应方面，国内外学者在转子的定子端部绕组受力方面做了较多的研究工作，也有部分学者对于转子绕组的结构和受力情况进行了分析，理论上和实际应用中都取得了很多可喜的成果。文献[5]以国产600MW大型汽轮发电机端部结构为分析对象，对定子绕组端部的受力特性进行了理论研究，总结了出现极值点的位置规律。文献[6]在研究发电机磁场分布的基础上，利用虚位移原理，通过有限元方法研究计算得到了转子偏心前后绕组电磁力的分布图。欧美、日本等发达国家，由于经济发展快，电力行业更加成熟，在大机组转子材料的研究开发上、在转子热应力的计算上、在转子寿命损耗的评估上都取得了进展，成为可以借鉴的经验[7-9]。这些成果大多利用有限元分析方法，为本文的分析提供了很好的理论参考和技术借鉴。

本文以QFSN-600-2YHG汽轮发电机为研究对象，采用有限元分析方法对气隙静态偏心下转子绕组进行分析，得到了转子绕组的变形、应力及应变，总结出了极值点出现的位置，可以对转子结构的优化和绕组固定的设计提供参考。

1　绕组受力及其力学响应分析

1.1分析对象简介

本文分析对象为QFSN-600-2YHG型汽轮发电机励磁绕组。该型发电机转子共32槽，分布如图1(a)所示。

转子每极下共有8组线圈，其中1号线圈为6匝、2～8号线圈为8匝。每匝导体由上下两根铜排组成。每个线圈由2段直线部分、2段圆弧部分和4个圆角部分组成。各部分均单独加工制造后经中频感应钎焊焊成一体，其中直线部分嵌装在转子齿槽中，并通过槽楔、槽封实现限位和固定；圆弧部分为励磁绕组端部部分，置于转子齿槽外部。N极线圈和S极线圈串联后组成完整的转子线圈，如图1(b)所示。

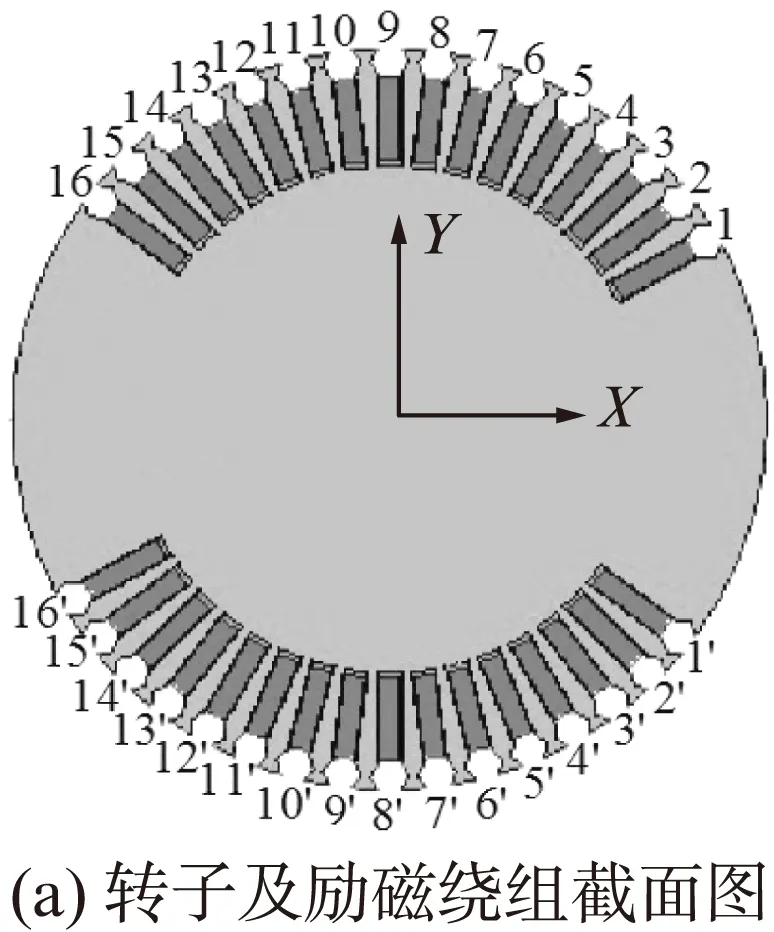
图1　汽轮发电机转子励磁绕组结构示意图

1.2转子绕组受力分析

气隙静态偏心主要通过改变定转子间的气隙径向长度分布来影响发电机的气隙磁导，但对气隙磁势影响较小。发电机的气隙磁密由气隙磁势和气隙磁导相乘得到。气隙静态偏心情况下，发电机的气隙分布和定转子磁势关系如图2所示。

图2　发电机偏心气隙及其磁势示意图

基于图2，空间角度α处的气隙磁动势分布可写为

f(α,t)=Fscos(ωt-α)+

Frcos(ωt-α+2π+ψ)

(1)

式中：Fs——定子绕组基波磁势幅值；

ω——电角频率，ω=2πf；

Fr——转子绕组基波磁势幅值；

ψ——发电机内功角。

不同周向位置的气隙磁导经幂级数展开并忽略二次以上高次谐波分量后为

Λ0(1+ζcosα)

(2)

式中：μ0——磁导率；

δ0——无偏心时气隙大小；

ζ——相对偏心率，ζ=e/δ0；

e——绝对偏心值，见图2(a)；

Λ0——无偏心时的气隙磁导，Λ0=μ0/δ0。

所以绕组I处的磁密可描述为

B′(αI,t)=f′(αI,t)·Λ′(αI,t)=Λ0[FscosαI+

Frcos(2π+ψ-αI)][1+

(3)

因此，绕组I所受电磁力为

FI0+FI0ζcos(αI-ωt)

(4)

式中：l、i—绕组的长度和电流；

1.3绕组力学响应分析

由式(4)可知，气隙偏心时转子绕组I上所受的电磁力由两部分组成。一部分为无偏心时电磁力FI0，另一部分为偏心所产生的增量ΔFI0，两者的变化趋势分别如图3和图4所示。对于某一固定槽号的绕组而言，其FI0恒定，不随时间变化(在转子转动过程中，各槽绕组与气隙磁场相对静止，均以同步速同向旋转)，但不同绕组的电磁力在空间分布上符合余弦性变化规律。由于只有一对极，所以应力和应变与电磁力一样，在空间上呈现对称性。ΔFI0为脉动循环变载荷，各绕组间相差一定的相位角，但其幅值较小，所以偏心时绕组力学响应依然会保持其空间对称性。

图3　无偏心时电磁力

图4　静偏心下1-8槽绕组受力情况

由图3、图4可知，电磁力在靠近大齿处(磁极处)最大，力学响应会随着与大齿距离的增大而减小。定性而言，由于转角处形状突变，易存在应力集中，所以这就是最有可能出现的最大应力位置。

2　励磁绕组力学响应计算

2.1励磁绕组模型建立

本文采用三维建模软件SolidWorks完成对转子绕组三维模型的建立。由于转子绕组在N极和S极上具有对称性，首先扫描得到一极转子绕组的三维图，然后把转子绕组零件模型保存成两份进行装配，在装配好了的基础上再画出一根线匝使N极绕组和S极绕组串联起来即可得到完整的转子绕组模型，如图5所示。

图5　励磁绕组三维模型

2.2静态响应分析

在Ansys Workbench中导入所建模型，定义材料为copper alloy，进行自动网格划分。转子绕组安装在转轴的转子绕组槽里，转子绕组的固定只有其直线部分，且视为弹性固定，又由于转子绕组的直线部分顶面与底面、左侧面与右侧面的弹性固定可以等效在顶面和其中一个侧面，所以在分析设置时仅需要在绕组直线部分的顶面与一个侧面添加弹性支撑即可。之后对各绕组的直线、圆弧和转角部分添加载荷。本文参考文献[5]得到的转子绕组电磁力幅值的分布图，将数据汇总得到表1。由表1可见，电磁力幅值并非随着与大齿距离的增大而减小，这是由槽的结构不同造成的。由于有限元仿真中设置转子绕组的边界条件时，需要加载的是平均压力，故表1中将电磁力转化为平均压力。需要提出的是，编号在同一行的绕组虽然它们的压力值大小相同，但是方向是相反的，现设定同一行的绕组，编号小的压力值为正，编号大的压力值为负。

表1　各绕组的电磁力

图6是转子绕组在静态电磁力下的变形结果放大670倍后的效果图。从图6中可知，转子绕组变形最大的地方发生在转子绕组的起始位置(8号绕组端部)，变形量为1.1198mm。这是因为转子绕组的端部不像转子绕组的直线部分那样有弹性支撑，并且8号绕组所受的压力是最大的。转子绕组变形最小的地方发生在N极绕组和S

图6　转子绕组在静态电磁力下的变形结果

极绕组串联线匝上，变形量为0.32004mm。N极绕组和S极绕组在轴向上有一定的滑移，这是N极绕组和S极绕组相对应的绕组的变形量大小有些许差异的原因之一。从总体上说，N极绕组和S级绕组的变形是对称的。

图7是转子绕组在静态电磁力下的应变结果放大670倍后的效果图。从图7中可知，转子绕组应变最大的地方发生在8号绕组的第一个转角处，应变量为4.882×10-6，这是因为8号绕组的端部变形最大，在绕组的转角部分形成了最大的应变。转子绕组的直线部分几乎都是转子绕组应变最小的地方，应变量为1.7955×10-9，这是因为转子绕组的直线部分固定在转轴的转子绕组槽里面，并且有槽楔等弹性支撑。此外，大部分绕组应变最大的地方都发生在绕组的转角部分，小部分绕组应变最大的地方发生在绕组的圆弧部分。从总体上说，N极绕组和S极绕组的应变是对称的。

图7　转子绕组在静态电磁力下的应变结果

转子绕组在静态电磁力下的应力结果如图8所示。从图8中可知，转子绕组应力最大的地方发生在8号绕组的第一个转角处，应力值为5.2794×105Pa，这也是造成8号绕组端部的应变最大的原因。转子绕组的直线部分几乎都是转子绕组应力最小的地方，应力值为157.48Pa。同样，这是因为转子绕组的直线部分固定在转轴的转子绕组槽里面，并且有槽楔等弹性支撑，不容易引起转子绕组的应力。对于整个转子绕组来说，

图8　转子绕组在静态电磁力下的应力结果

其应力大体上是对称的。多数绕组的最大应力发生在它的转角部分，一些绕组的最大应力发生在圆弧部分，比如说15、16号绕组。

2.3瞬态响应分析

转子绕组在变载荷下的变形结果放大44000倍后的效果图如图9所示，需要指出的是，变形结果选取的是0.02s时刻下的。由图9可见，转子绕组变形最大的地方发生在2号绕组和15号绕组的直线部分，此外，还有小部分发生在8号绕组的端部(起始的圆弧部分)，最大变形量为4.47×10-3mm。转子绕组变形最小的地方发生在9、10、11、12、13号绕组的转角部分，最小变形量为6.5528×10-6mm。就整个转子绕组来说，这一时刻下其变形是对称的，而且转子绕组变形量变化的趋势是靠近大齿的绕组向远离大齿的绕组逐渐减小。另外，转子绕组也有一定的轴向滑移。

图9　转子绕组在变载荷下的变形结果

图10为转子绕组在瞬态电磁力下的应变结果放大44000倍后的效果图。由图10可见，转子绕组应变最大的地方发生在16号绕组的圆弧部分以及1号绕组的转角部分，最大应变量为1.9751×10-7。转子绕组的直线部分几乎都是转子绕组应变最小的地方，最小应变量为3.8537×10-12mm，并且，N极绕组的最大应变主要发生在绕组的转角部分，S极绕组的最大应变主要发生在绕组的圆弧部分。

图10　转子绕组在瞬态电磁力下的应变结果

图11为转子绕组在瞬态电磁力下的应力结果放大44000倍后的效果图。由图11可知，转子绕组应力最大的地方发生在16号绕组的圆弧部分，最大应力为21390Pa。N极绕组的圆弧部分和整个绕组的直线部分均是最小应力发生的地方，最小应力为0.3939Pa

图11　转子绕组在瞬态电磁力下的应力结果

2.4对比分析

对比图6和图9可知，转子绕组静态电磁力下的变形要比瞬态电磁力下的大3个数量级，但是瞬态电磁力下N极绕组与S极绕组变形的对称性要比静态电磁力下的好。另外，静态电磁力下转子绕组的轴向滑移要比瞬态电磁力下的更为明显。

对比图7和图10可知，转子绕组的应变在静态电磁力下和瞬态电磁力下是相近的，并且，其最小应变都主要发生在转子绕组的直线部分，最大应变主要发生在转子绕组的转角部分。

对比图8和图11可知，虽然静态电磁力下的应力要比瞬态电磁力下的大1个数量级，但是应力在转子绕组上的分布大体一致，绕组转角部分或圆弧部分的应力比较大，绕组直线部分的应力比较小。这一结论与现场实际检修时所发现的结果相一致。图12为某厂经长期气隙偏心运行后励磁绕组的变形情况。由图12可以看出，绕组变形主要集中在转角和圆弧部分。这与本文理论分析和有限元计算所得的结果一致。

图12　某厂经长期气隙偏心运行后的绕组变形

3　结　语

本文对600MW汽轮发电机气隙静态偏心下的励磁绕组受载及其力学响应进行了分析，结论如下：

(1) 不论是否存在气隙静态偏心，汽轮发电机励磁绕组的变形、应变和应力在整体分布上具有一定的空间对称性。

(2) 转子绕组变形量从靠近大齿的绕组向远离大齿的绕组逐渐减小，且存在轴向滑移；转角部分应力和应变最大，直线部分的应变和应力最小；1、16、2、15、8号绕组的转角和圆弧部分较为危险。

(3) 有限元仿真结果与理论分析一致，对转子结构优化及绕组固定的设计具有一定的参考价值。

[1]PATSIOS C， CHANIOTIS A， TSAMPOURIS E， et al. Particular electromagnetic field computation for permanent magnet generator wind turbine analysis[J]. IEEE Transactions on Magnetics, 2011，46(8)： 2751-2754.

[2]刘飞,梁霖,徐光华,等.基于电流信息的电机回转偏心检测方法[J].电工技术学报,2014,29(7)： 181-186.

[3]唐贵基,何玉灵,万书亭,等.气隙静态偏心与定子短路复合故障对发电机定子振动特性的影响[J].振动工程学报,2014,27(1)： 118-127.

[4]ZHANG G Y， WEI J C， HUANG H Z， et al. A study on the nonlinear vibration of the generator rotor based on the unbalanced electromagnetic force and the oil film force coupling model[J]. Journal of Vibroengineering， 2013，15(1)： 23-36.

[5]张文战.汽轮发电机定转子电磁力分析及其应用研究[D].保定： 华北电力大学，2010.

[6]闫雪超. 大型汽轮发电机转子偏心磁场分析与电磁力计算[D].哈尔滨： 哈尔滨理工大学，2013.

[7]LEMAITRE J, CHABOEHE J L. Mechanics of solid materials [M]. Cambridge： Cambridge University Press, 1998.

[8]VISWANATHAN R. Damage mechanism sand life assessment of high-temperature components [J]. ASME International, 1989(1)： 49-62.

[9]李川，王明渝.高水头冲击式水轮发电机组交流励磁与调速协调控制策略[J].重庆理工大学学报(自然科学版)，2014(9)： 108-111.

Exciting Winding Load and Mechanical Response of Turbo-Generator under Static Air-Gap Static Eccentricity Fault*

JIANGHongchun1,WUShiliang2,HEYuling1,ZHONGHao1，TANGGuiji1

(1. Department of Mechanical Engineering， North China Electric Power University， Baoding 071003， China；2. Liuzhou Power Generating Co., Ltd.， Liuzhou 545000， China)

The acting load and the mechanical response of the exciting windings were investigated, taking QFSN—600-2YHG type turbo-generator as the study object. The 3D model of the exciting winding was firstly set up in SolidWorks and imported into Ansys. Then the corresponding mechanical response of the windings under the load generated by the air-gap eccentricity was calculated. The result showed that the deformation, the strain, and the stress of the winding were symmetric. The winding bars which were more near the main slot had a larger deformation. The stress and strain at the corner parts of the winding had the largest values, while at the straight line parts the values were the smallest. The corner arcs of the winding in Slot 1,16,2,15, and 8 were the most dangerous positions. The achievements offered a reference for the structure design and the winding fix improvement of turbo-generator.

turbo-generator； exciting winding； air-gap static eccentricity； mechanical response

国家自然科学基金项目(51307058)；河北省自然科学基金项目(E2015502013；E2014502052)；中央高校基本科研业务费专项基金项目(2015ZD27)

蒋宏春(1982—)，女，博士研究生，讲师，研究方向为电站设备状态监测，机械设计及理论。

何玉灵(1984—)，男，博士，副教授，研究方向为电站设备状态监测、控制与节能，振动分析与控制，系统动特性分析与改进。

TM 311

A

1673-6540(2016)08- 0046- 05

2016-03-25