改进的超椭圆曲线有序多重盲签名*

杨　青

(西安航空学院理学院　西安　710077)



改进的超椭圆曲线有序多重盲签名*

杨青

(西安航空学院理学院西安710077)

对已有文献提出的有序多重签名方案进行了分析和改进,提出快速和高效的基于超椭圆曲线的有序多重盲签名方案,并给出具体算法。比较和分析了改进方案的复杂度和安全性,与已有文献比较,改进方案的运算时间减少了2nTH+59.616n-38.87毫秒。改进方案具有运算量低,所需时间少,安全性高且易于实现等优点。

超椭圆曲线; 约化除子; 盲签名; 多重签名

Class NumberTP309

1　引言

1989年Koblitz[1]提出了超椭圆曲线密码体制,其安全性是建立在超椭圆曲线的Jacobian群离散对数问题上的。与椭圆曲线密码体制相比,超椭圆曲线的安全性更高,所用基域更小。在相同的安全强度下,RSA所用的基域为1024bit,椭圆曲线所用的基域为160bit,而对亏格为2的超椭圆曲线所用基域为80bit,对亏格为3的超椭圆曲线所用基域约为55bit。为了满足我们的安全需要[2],在超椭圆曲线上建立阶为2160大小的群。当亏格为3时,也要选择安全的超椭圆曲线以避免攻击[3]。

盲签名是指签名者只是完成对文件的签名工作并不了解所签信息的内容。它具备盲性和不可追踪性,在电子投票和银行电子现金系统方面具有广泛的应用。在1983年,chaum首次提出盲签名概念,并建立了基于RSA的盲签名方案[4]。多重数字签名是指多个人合作对同一份消息进行签名。在1994年,Harn L提出了基于Meta-ElGamal方案的多重签名方案[5]。签名者按照串行的顺序进行签名称为有序多重签名。如文献[6～7]是将椭圆曲线双线性对用于多重签名方案。

本文对文献[13]的多重签名方案进行了分析和改进,提出了更为快速和高效的基于超椭圆曲线的有序多重盲签名方案。分析签名结构,给出具体签名算法和验证算法,并且证明了算法的正确性和安全性。最后,比较和分析了改进方案的安全性和复杂度,应用于超椭圆曲线密码系统。该算法具有快速、高效且易于实现的特点。在有序签名结构中,签名者的公钥按照签名顺序的倒序生成,由后往前依次生成,可以避免在生成公钥时出现重复,节省计算量。

2　超椭圆曲线密码系统

本文略去对超椭圆曲线的有关概念的介绍,具体内容可参考文献[9～11]。构造一个映射函数φ[12]:J(C;Fq)→Zq2g,φ是一个从超椭圆曲线的Jacobian群中的元素到有限整数集的单射函数。

Zq2g={0,1,…,q2g-1},

φ(D)=ag-1q2g-1+…+a1qg+1+a0qg

+bg-1qg-1+…+b1q+b0

3　改进的有序多重盲签名方案

该算法有t个签名者(也称签名节点),签名过程可由消息发送者I,签名收集者C和t个签名者实现。

签名顺序为(A1,1,…,A1,i,…A1,t),A1,i为第i个签名者。

3.1签名者公钥的生成

有序签名者的公钥按照签名顺序的倒序生成,最后一个签名者A1,t的公钥由超椭圆曲线C上Jacobian群的一个基元D生成。所有签名者的公钥和私钥生成如下:

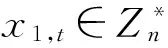
当所有签名者的公钥生成完后,系统公布签名顺序和所有签名者的公钥。每个签名者保存自己的私钥,并且系统公开参数还有超椭圆曲线C(Fq),φ,n,D。

3.2生成R

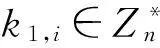
3.3盲签名的生成和验证

3.3.1消息m的盲化

3.3.2验证并生成签名

每一个签名者收到前一签名者的签名后,首先验证此签名是否有效。若之前签名有效,则继续签名,然后将自己的签名发送给下一位签名者;否则,拒绝签名。

1) 签名者A1,i进行如下步骤:

(1)A1,i收到A1,i-1的签名后,验证方程e=s1,i-1Y1,i+φ(R)Q1,i-1是否成立。若成立,则继续下一步骤,否则要求A1,i-1重签或拒绝签名。(A1,1不需验证)。

(2)A1,i计算s1,i=x1,is1,i-1-k1,iφ(R)modn,Q1,i=Q1,i-1+R1,i其中,s1,0=m′,Q1,0=0,Q1,t=R,(1≤i≤t)。并传递数组(s1,i,Q1,i)给A1,i+1。

2) 后续签名者A1,i+1,…,A1,t按照本节介绍的方法进行签名及验证。将最后一位签名者A1,t的签名(s1,t,Q1,t)作为m′的有序多重盲签名,发送给签名收集者C。C验证等式:e=s1,tD+φ(R)Q1,t是否成立。若成立,则宣布签名有效;否则无效。最后,C验证A1,t的签名有效后,则发送签名s1,t给消息发送者I进行脱盲变换,否则终止签名。

3.3.3盲签名的脱盲和验证过程

消息发送者I收到签名收集者C发送的签名s1,t后,计算s=(m′)-1ms1,t-βφ(H)。验证等式:mY1,1=sD+φ(H)H,若成立,则I宣布消息m的签名有效,否则无效。

4　算法正确性证明

定理1若等式e=s1,iY1,i+1+φ(R)Q1,i成立,则有序签名者A1,1,…,A1,i的签名有效。

证明:∵s1,i=x1,is1,i-1-k1,iφ(R)modnx1,i,s1,i-1=s1,i+k1,iφ(R)modn

∴x1,is1,i-1Y1,i+1=s1,iY1,i+1+k1,iφ(R)Y1,i+1,s1,i-1Y1,i=s1,iY1,i+1+φ(R)R1,i当i=1,2…,时,有

等式左右两端相加,得s1,0Y1,1=s1,iY1,i+1+φ(R)Q1,i。

∵s1,0=m′

∴e=m′Y1,1=s1,iY1,i+1+φ(R)Q1,i

定理2若等式mY1,1=sD+φ(H)H成立,则原始消息m的有序盲签名有效。

证明:∵由定理1的证明可知s1,i-1Y1,i=s1,i·Y1,i+1+φ(R)R1,i成立。

∴e=m′Y1,1=s1,iY1,i+1+φ(R)Q1,i

∴当i=t时,m′Y1,1=s1,tY1,t+1+φ(R)Q1,t

∵Y1,t+1=D,Q1,t=R

∴m′Y1,1=s1,tD+φ(R)R

又∵m′=α-1φ(H)-1φ(R)mmodn

∴α-1φ(H)-1φ(R)mY1,1=s1,tD+φ(R)R

∴s1,tD=α-1φ(H)-1φ(R)mY1,1-φ(R)R

∵s=(m′)-1ms1,t-βφ(H)

∴s=αφ(H)φ(R)-1s1,t-βφ(H)

∴sD=αφ(H)φ(R)-1s1,tD-βφ(H)D=αφ(H)φ(R)-1[α-1φ(H)-1φ(R)mY1,1-φ(R)R]-βφ(H)D=mY1,1-αφ(H)R-βφ(H)D=mY1,1-φ(H)(αR+βD)=mY1,1-φ(H)H

∴mY1,1=sD+φ(H)H

5　方案分析

5.1效率分析

1) 本文的有序多重盲签名方案分别与文献[8,13～14]的方案进行了效率分析,如表1、表2和表3。我们的操作平台是Pentium IV 3GHZ,512 MB RAM和Windows XP操作系统,运行时间单位为ms(毫秒)。在特征为2的域上,选取亏格为2的超椭圆曲线。Lange[15]给出亏格为2的超椭圆曲线除子加法和倍点运算的高效计算公式,除子加法运算的运算量为1I+3S+22M,除子倍点运算的运算量为1I+5S+22M,其中I,S,M分别表示有限域上的求逆、平方和乘法,1I=30M,1S=0.8。1THEM=56TML≈12.88ms,1THEA=55.4TML≈12.742ms。为便于比较计算量,假定签名者人数均为n,结果见表2、3。本文的有序多重盲签名方案总的计算量为(2n+3)THEM+2nTHEA+(n+1)TML,总的运算时间为51.014n+38.87(ms)。与文献[13]的有序签名比较,本文的运算时间减少2nTH+59.616n-38.87(ms)。由表3知,与文献[8,14]相比本文提出的方案具有最少的运算量,所需时间最短,且易于实现等优点。

表1　各种密码体制下的操作运算转换关系(单位:ms)

表2　其他文献和本文方案的运算量比较

表3　已有文献和本文方案的运算时间(单位:ms)

5.2安全性分析

1) 方案满足盲性。首先将原始消息m盲化后为m′,然后每个签名者对m′进行签名。要求解原始消息m需要求解基于超椭圆曲线的离散对数问题,而这一问题在计算上是不可行的,因此本方案满足盲性。

2) 防止相邻签名者私自串通改变签名顺序。签名收集者事先确定签名顺序后,等所有签名者的公钥生成完后再公布。因为每个签名者在所有公钥生成完前并不知道前后签名者是谁,从而无法与相邻签名者串通,所以防止了相邻签名者调换签名顺序。同时,每个签者的公钥公开,对应的私钥是秘密的,想要求解私钥相当于求解基于超椭圆曲线的Jacobian群上的离散对数问题,这是不可行的,从而能够抵抗伪造攻击。

6　结语

本文改进了文献[13]提出的多重签名方案,提出改进的有序多重盲数字签名方案。并给出具体算法,更符合实际应用。最后,分析和比较了改进方案和已有文献的计算效率,得出改进方案具有运算量低,所需时间少,且易于实现等优点。同时,改进方案具有高安全性能。

[1] Koblitz N. Hyperelliptic Cryptosystems[J]. Journal of Cryptology,1989,1(3):139-150.

[2] Avanzi R, Cohen H, Doche C, et al. Handbook of Ellipic and Hyperelliptic Curve Cryptography[M]. Boca Raton: Chapman & Hall,2005:348-351.

[3] Li M, Kong Fy, Zhu Dm. Fast addition formulae for Montgomery Ladder scalar multiplication on hyperelliptic curves[J]. Journal of Software,2013,24(10):2275-2288.

[4] Chaum D. Blind signatures system[C]//proc. Of CRYPTO’83. New York. USA: plenum press,1983:153-153.

[5] Harn L. New digital signature scheme based on discrete logarithm[J]. Electronics Letters,1994,30(5):396-398.

[6] Islam S. H., Biswas G. P. Certificateless short sequential and broadcast multisignature schemes using elliptic curve bilinear pairings[J]. Journal of King Saud University — Computer and Information Sciences,2014,26:89-97.

[7] Islam S. H., Biswas G. P. Certificateless strong designated verifier multisignature scheme using bilinear pairings[C]//Proceedings of the international conference on advances in computing Communications and informatics(ICACCI-2012),2012b:540-546.

[8] Harn L, Lin Cy, Wu Ct. Structured multisignature algorithms[J]. IEE Computers and Digital Techniques,2004,151(3):231-234.

[9] Yang Siman, Wu Hongfeng, Li Jiyou. Access structures of hyperelliptic secret sharing schemes[J]. Finite Fields and Their Applications,2016,37:46-53.

[10] Blake I, Seroussi G, Smart N, et al. Advances in Elliptic Curve Cryptography[M]. London: Cambridge University Press,2005:133-149.

[11] Wollinger T. Software and hardware implementation of hyperelliptic curve cryptosystems[C]//Bochum: Ruhr- University of Bochum,2004:19-35.

[12] You Lin, Sang Yongxuan. Effective generalized equations of secure hyperelliptic curve digital signature algorithms[J]. The Journal of china universities of posts and telecommunications,2010,17(2):100-108.

[13] Chu Hongwei, Zhao Yinliang. Two efficient digital multisignature schemes[C]//Proceedings of the International Symposium on Computational Intelligence and Design (ISCISD’08),2008:258-261.

[14] Yang Fuw-Yi, Lo Jenghung, Liao Caiming. Improvement of an efficient ID-based RSA multisignature[C]//Proceedings of the International Conference on Complex, Intelligent and Software Intensive Systems,2010:822-826.

[15] Lange T. Formulae for arithmetic on genus 2 hyperelliptic curves[J]. Applicable Algebra in Engineering, Communication and Computing,2005,15(5):295-328.

Improved Sequential Blind Multisignature Scheme Based on Hyperelliptic Curves

YANG Qing

(School of Science, Xi’an Aeronautical University, Xi’an710077)

Sequential multisignature algorithm by reference is analyzed and improved. Fast and efficient sequential blind multisignature scheme based on hyperelliptic curves is presented. the complexity and security of improved scheme are compared and analyzed. Comparing with

, improved scheme reduces computation costs 2nTH+59.616n-38.87ms. The results show that improved scheme has the advantages of low computation complexity, low consumption of time, high security and easy to achieve.

hyperelliptic curve, reduced divisors, blind signature, multisignature

2016年3月7日,

2016年4月20日

陕西省科技厅项目(编号:2013JM1019;2014K05-43);陕西省教育厅项目(编号:14JK1310);西安航空学院项目(编号:2015KY1218)资助。

杨青,女,硕士,讲师,研究方向:信息与代数编码。

TP309DOI:10.3969/j.issn.1672-9722.2016.09.026