基于多种群遗传算法的直升机编队目标分配*

周　凯　姜文志　陈邓安

(海军航空工程学院　烟台　264001)



基于多种群遗传算法的直升机编队目标分配*

周凯姜文志陈邓安

(海军航空工程学院烟台264001)

针对多直升机目标分配问题,提出了一种基于多种群遗传算法的多直升机目标分配方法。多种群遗传算法根据多直升机目标分配问题的特点,设计了竞争算子和迁移算子,加强了个体与群体中最优个体进行信息交换,实现多种群的协同进化的同时有效避免陷入局部最优,较为显著地提升了原算法的性能。仿真结果表明:多种群遗传算法能够有效解决多约束条件下多直升机目标分配问题,并且算法简单、灵活,易于实现和扩展。

多直升机协同; 目标分配; 多种群遗传算法

Class NumberV271.4; TP202

1　引言

直升机所具有的超机动和低空飞行的能力,适宜低空或者超低空作战。作为打击地(海)面和超低空中各种目标的主要装备,同时也是支援地(海)面和空中力量的重要保障,其主要作战方式是对面进行攻击[1]。在直升机作战应用中,直升机不仅仅以一个独立的个体存在于战场,而在大多数情况下,是以编队的形式出现。本文在研究直升机编队对海面多目标攻击问题时,与传统一对一相比,最显著的差别就是面对多个敌方目标需要根据我方资源为编队成员分配目标,主要考虑多个直升机之间如何进行冲突消解,有效并快速地完成多机多目标分配问题[2～3]。

神经网络,蚁群算法,粒子群算法等多种人工智能方法在协同目标分配决策领域有着非常好的应用前景。文献[4]中建立了较为一般化的防空火力分配的数学模型,并重新推敲了约束条件,设计了较为具体合适的遗传算法,并通过仿真实现了目标分配,得到了较优的结果,但数据量增大时,有可能出现早熟现象或者求解速度过慢甚至陷入停滞[4]。在传统算法中嵌入新的机制作为提高算法优化性能的一个重要且有效的途径,开发和应用实践表明,并行遗传算法都能不同程度地达到这要求。文献[5]通过随机和人为构造了种群,独自进行遗传操作,考虑到染色体的多样性,每个处理器都将自己最好的个体传送个相邻,相比基本遗传算法优势明显,能够使解空间很好的脱离早熟,得到最优解,但当规模扩大,复杂度增加时,其设计的遗传算法求解过程中求解时间较长[5]。为此,通过对复杂环境约束下的任务环境研究多机多目标分配问题分析,同时考虑到对寻优能力和快速性的双重要求,本文使用多种群遗传算法,在进化过程中增加了较好个体在群体中的传播,同时降低传输数据传输消耗,提高收敛速度和解的精度[6～8]。适宜应用到多机编队对水面快速目标打击的目标分配问题中。

2　直升机编队作战问题描述

2.1作战流程

直升机作战的基本流程是:收到敌目标情报→目标探测→数据处理(建立敌我态势图)→目标分配→方案制定→作战实施→打击效果评估,满足打击要求则执行其他任务,否则重新进行威胁判断并进行目标分配,继续打击。

根据直升机作战任务的流程分析,编队协同攻击的作战关系图如图1所示。

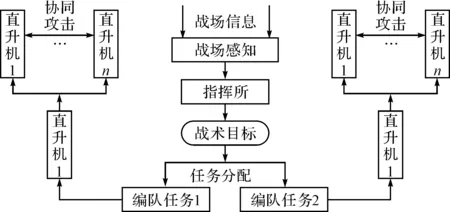
图1　编队作战关系图

2.2作战收益函数的构造

为了便于目标分配后续的量化计算,首先应该确定敌我相对作战能力。为此,通过以下的我机作战能力、优势度函数、快艇作战能力、目标相对价值来确定总的我相对敌作战收益函数值。

1) 直升机作战能力

直升机攻击能力由航程指数和武器效能指数两部分组成。两者相加得出的总值。航程指数是当量航程的自然对数,武器效能指数是当量载弹量的自然对数。主要影响因素最大航程、突防系数、远程武器系数、导航能力系数和最大载弹量和对地攻击效率系数[9]。计算公式如下:

ZF=[ln(N)+ln(M)]ε1ε2

(1)

N=R×Re×Rm×Rn

(2)

M=WB×Pa

(3)

式中N为当量航程,M为当量载弹量,ε1为电子对抗系数,ε2为探测能力系数,R为最大航程、Re为突防系数、Rm为远程武器系数、Rn为导航能力系数、WB为最大载弹量和Pa对面攻击效率系数由于作战能力指数与优势度指数差距比较大,需要对其进行处理,这里取直升机作战能力所占比重:

Li=ZFi/max(ZFi) (1≤i≤n)

(4)

2) 直升机优势度分析

直升机在执行打击过程中,编队成员会耗费自身资源的同时,还会受到来自地面目标的攻击。在打击过程中,直升机暴露在目标区域内,直升机能够成功打击目标不仅与编队成员的自身状态有关,同时与每一架直升机的态势有关,如位置、速度与目标距离;相对于打击目标的优势越好,则成功摧毁目标而保存自己的可能性越大。单纯考虑直升机和地面目标的毁伤能力是不实际的,只能单纯的给出毁伤值的累加。因此,在模型中引入优势函数S,它主要由相对距离优势Dij、相对速度优势Vij和相对角度优势Tij共同决定。理论分析和实战经验都表明:在具有角度优势的情况下,相对距离越大优势越小;距离越小,距离优势越大[10]。因此,角度优势和距离优势宜处理为相乘关系:

Sij=β1Vij+β2Dij×Tij

(5)

其中,β1、β2为权系数(0≤β1、β2≤1),具体的计算方法可借鉴文献[1,11]。

3) 快艇作战能力

将快艇作战效能作为总目标,结合快艇的系统特点,主要由四个方面组成侦查探测能力、作战指挥能力、武器系统能力、本艇生存能力。

ZM=Ef×Ep×Et×Em

(6)

式中ZM表示快艇作战能力,Ef表示侦查探测能力指数,Ep表示快艇作战指挥能力指数,Et表示本艇生存能力指数,Em表示武器系统能力指数(主要考虑舰炮对直升机的毁伤能力)。

4) 目标相对价值评估

导弹快艇目标价值评估主要来源于上一级指挥信息,主要考虑到导弹快艇对舰艇编队成员的威胁,选用以下几个因素来描述武器系统能力:导弹射程因素Rp;制导能力Gp;杀伤能力系数Yp;数量指数N[12]。因此,水面快艇对舰船的威胁指数计算模型可表示为

(7)

同时指挥舰更倾向于具有成功打击目标能力的直升机去攻击敌快艇解除威胁,构造期望权重矩阵Wij,目标相对价值Qij为

Qij=Wij×Edj

最后,直升机得到的相对于目标的作战能力效益值为

Fij=α1(LiSij/ZMj)+α2Qij

(8)

其中,α1、α2为权系数(0≤α1、α2≤1)。

则总的作战能力效益值为

(9)

3　多种群遗传算法目标分配研究

3.1目标分配的数学模型

基于作战效益函数,可构造直升机编队目标分配问题模型如下:

(10)

相应的约束条件:

目标分配时,每个目标均须分配一架直升机对其进行打击,即

对编队中的每一架直升机,至少给其分配一个地面目标,即

由于单架直升机配置的武器数量有限,且为保证直升机在目标区域内滞留的时间不至于过长,要求每架直升机攻击的目标的个数不能超过某个值[13],记各架直升机可攻击的目标的最大个数所组成的向量B=[b1b2…bn-1],则有

3.2单种群遗传算法

遗传算法(Genetic Algorithm,GA)是一种进化算法,通过对生物遗传和进化过程中选择、交叉、变异机理的模仿,来完成对问题最优解的自适应搜索过程[14]。遗传算法是通过给解向量编码、形成初始种群,然后用变异、交叉重组、自然选择等算子,进行反复迭代,最终求得最优解。GA算法的主要步骤如下:

1) 构造染色体

遗传算法编码方式采用二进制编码,利用长度为n×m的一维数组来表示矩阵Xn×m该数组可平均分成m段,每段都表示每一直升机所分配的目标的情况,1表示该目标被分配到此直升飞机去攻击,0表示该目标没有被分配到此直升飞机。

2) 个体适应度评价

3) 遗传算子

选择操作主要建立在对个体的适应度进行评价的基础之上。操作的主要目的是为了避免基因缺失、提高全局收敛性和计算效率。最常用的选择算子是基本遗传算法中的比例算子。交叉运算是遗传算法中产生新个体的主要操作过程,它以某一概率相互交换某两个个体之间的部分染色体。其具体操作过程是:先对群体进行随机配对;其次随机设置交叉点位置,其中的数字表示交叉点设置在该基因座之后;最后再相互交换配对染色体之间的部分基因。变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进行改变,它也是产生新个体的一种操作方法,首先确定出各个个体的基因变异位置,然后按照某一概率将变异点的原有基因支取反。

群体规模和遗传控制参数的设定均对GA算法的优化性能有较大的影响。当群体规模较小时,群体中的多样性程度降低,个体竞争性比较弱,随着进化的进行,群体很快趋于单一化,交叉操作产生新个体的作用渐趋消失,群体的更新只靠变异操作来维持,群体很快终止进化;当群体规模取值较大时,势必造成计算量的增加。遗传控制参数的设定涉及GA算法全局搜索和局部搜索能力的均衡,不恰当的设定很容易产生早熟、局部寻优能力较差等现象。

3.3多种群遗传算法

为了克服基本遗传算法所存在的上述问题,避免算法陷入局部最优解,引入多种群遗传算法进行改进,通过迁移算子[15]进行联系,实现多种群的协同进化,综合结果获取最优解。由于控制参数的设定在很大程度上影响算法的性能,各个种群取不同的控制参数,通过多个设有不同控制参数的种群协同进化,同时兼顾了算法的全局搜索和局部搜索。同时借助迁移算子把相对独立的种群联系起来,在进化过程中,把最优个体定期地引入其他种群,实现了种群之间的信息交互,保证了种群的多样性。个体自身进化修正策略的引入,各个个体分别与周边个体进行竞争与合作操作,在保留自身原本有用信息的基础上吸收最优邻居个体的有益信息,以实现有益信息在种群中的流动[16]。精华种群是在进化的每一代,通过人工选择算子选出其他种群的最优个体放入精华种群加以保存。算法结构图如图2所示。

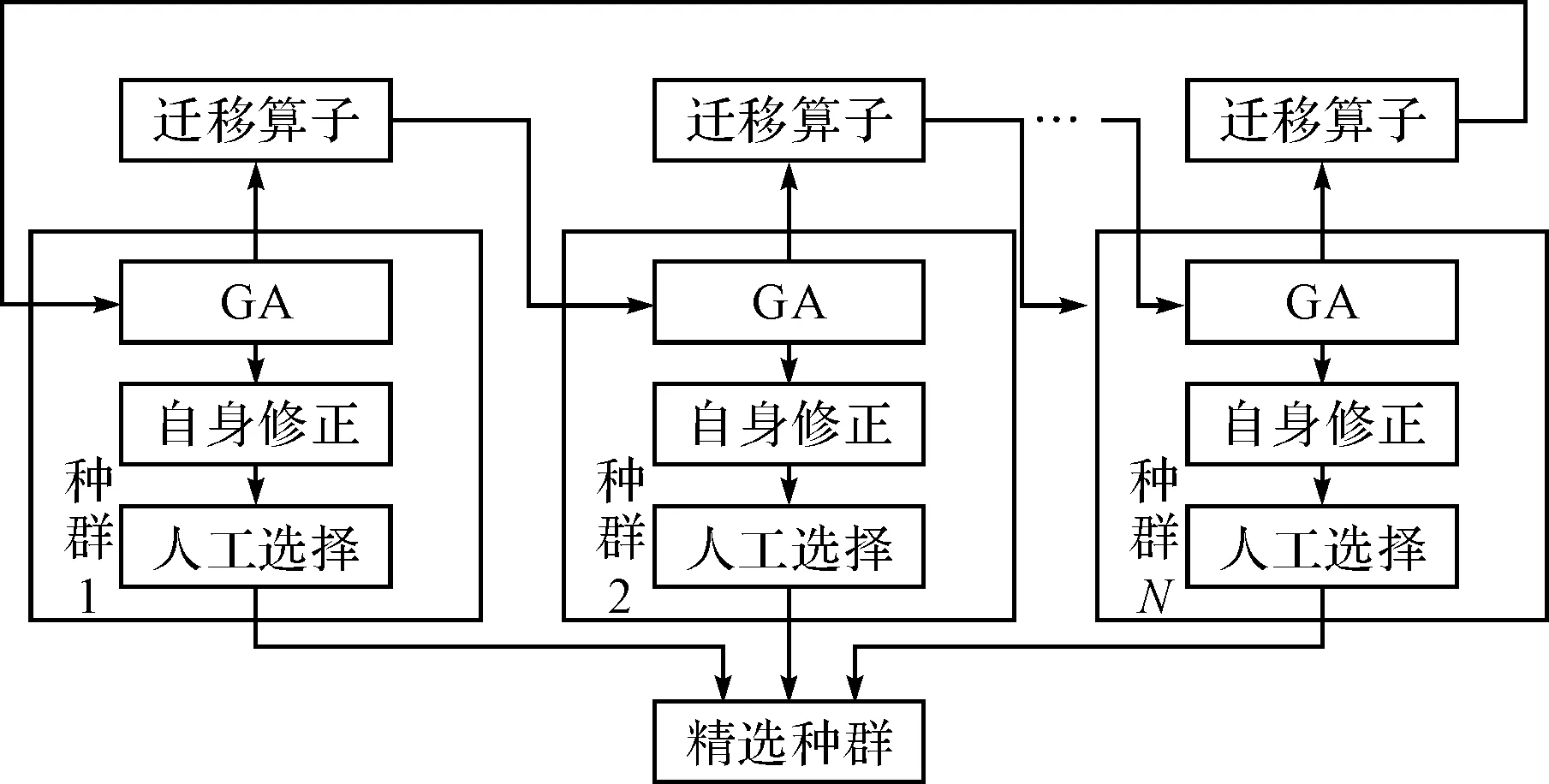
图2　多种群遗传算法结构图

3.4多种群算法描述

步骤1:遗传代数计数器初始化:gen←0,种群数目:MP。

步骤2:随机初始化群P1(t),P2(t),…,PMP(t)。

步骤3:分组计算各Pi(t)(i=1,2,…,MP)中个体的适应度。

由变异算子进行变异操作:

P‴i(t)←Mutate[P″i(t)]

步骤5:交叉和变异采用如下公式随机产生,从而保证MP个种群在不同的控制参数下协同进化在同步进化分组计算各P‴i(t)(i=1,2,…,MP)中个体的适应度。

Pc=0.7+(0.9-0.7)*rand(MP,1)

Pm=0.001+(0.05-0.001)*rand(MP,1)

步骤6:通过迁移算子immigrant把目标种群最劣的个体替换为源种群最优种群。

步骤7:人工选择算子将各种群最优个体存入精华种群。

步骤8:根据竞争算子,由周边个体进行竞争与合作操作,并记录更新各自适应度。假设Q‴ik(t)为第i个种群个体P‴ik(t)的几个邻居中拥有最大适应值的个体,P‴ik(t)在解空间的位置根据

P‴ik(t)′=Q‴ik(t)+rand(-1,1)(Q‴ik(t)-P‴ik(t))

i=1,2,…,MP

进行调整。k为每个种群中的个体数。

步骤9:终止条件判断:若不满足条件,则gen←gen+1,转向步骤4;若满足终止条件,则:输出优化结果,算法结束。

3.5实例验证

为了测试算法的性能,以直升机编队对海面敌快艇进行打击的目标分配问题为研究对象进行仿真实验。想定直升机编队共有5架直升机,面临敌5个水面目标,这5个目标对编队的威胁程度和收益值各不相同。根据直升机作战收益定义,计算得到直升机作战能力的相对比重如表1所示。优势度以及水面目标参数见表2～表4。

表1　直升机作战能力

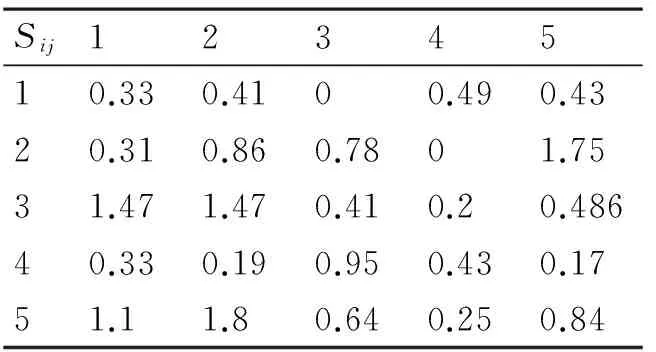
表2　直升机相对于目标的优势度

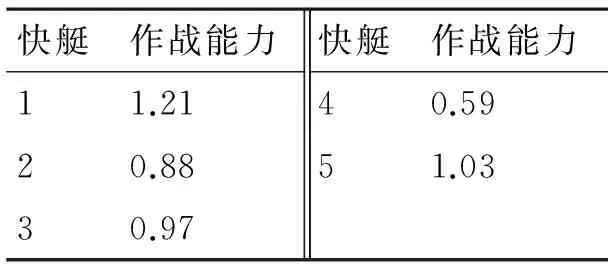
表3　快艇作战能力

表4　目标相对价值

取种群规模N=5,种群数量MP=5,保持最优值代数MAXGEN=30,交叉和变异概率分别在(0.7～0.9)和(0.001～0.05)随机取得的,而基本遗传算法采用种群规模25,进化代数30,交叉和变异分别为0.9和0.05控制参数。通过Matlab进行仿真验证,最优目标分配方案对应的最大收益值为:8.7766,对应的自变量取值:25431,即分配矩阵为

对比仿真结果,可以看出两种算法,均能收敛到最优的目标函数,但本文提出的多种群遗传算法收敛速度比基本遗传算法要快,平均在第6次迭代时达到最大收益值,而基本遗传算法需要13次迭代,如图3所示。虽然该算法融入新的机制在时间消耗方面有所增多,但在权衡寻优效率与寻优结果精度的基础上,本文提出的多种群遗传算法应用到目标分配在计算效率上有优势。

图3　两种算法的收敛速度比较

4　结语

本文首先分析了直升机作战过程,结合影响直升机对地作战的主要因素,建立了相应的数学模型,利用具有自适应全局搜索能力的遗传算法来解决直升机编队目标分配问题。针对遗传算法局部搜索能力弱的缺点,引入多种群遗传算法能够更快地寻求到全局最优值,从而提高了遗传算法的收敛速度和解的精度。算法实例表明,基于多种群遗传算法搜索能力好,收敛速度快,能够保证直升机对水面快速目标的打击。

[1] 麻士东,龚光红,等.目标分配的蚁群_模拟退火算法及其改进[J].系统工程与电子技术,2011,33(5):1183-1186.

MA Shidong, GONG Guanghong, et al. Hybrid srtatagy with ant colony and simulated annealing algorithm and its improvement in target assignment[J]. Systems Engineering and Electronics,2011,33(5):1183-1186.

[2] 浦鹏,张金春,孙喜菁.多机协同多目标分配战术决策研究[J].战术导弹技术,2007(2):57-61.

PU Peng, ZHANG Jinchun, SUN Xijing. The study of tactical decision of multi-target distribution in cooperative air combat[J]. Tactical Missile Technology March,2007(2):57-61.

[3] Liu Y F, Zhang A. Cooperative task assignment method of manned/unmanned aerial vehicle formation[J]. Systems Engineering and Electronics,2010,32(3):584-588.

[4] 季大琴.舰艇编队防空火力基于遗传算法的分配方案[J].军事运筹与系统工程,2007,21(1):37-40.

JI Daqin. Warship fomation air defense weapon-target assignment based on genetic algorithm[J]. Militrary Operations Research and Systems Engineering,2007,21(1):37-40.

[5] 季大琴,宋剑,范婷婷.基于并行遗传算法的舰艇编队防空火力分配方案[J].哈尔滨师范大学自然科学学报,2011,27(1):58-60.

JI Daqin, SONG Jian, FAN Tingting. Warship fomation air defense weapon-target assignment based on parallel genetic algorithm[J]. Natural Seiences Journal of Harbin Normal University,2011,27(1):58-60.

[6] Min C P, Shen L C. Hybrid genetic algorithem and constraint handling formultiple UCAV mission assigning[J]. Control and Decision,2006,21(7):781-786.

[7] Ye W, Zhu A H, Pan C P, et al. Cooperation mission assignment algorithm for multi-UCAV[J]. Systems Engineering and Electronics,2010,32(1):104-108.

[8] 任少伟,贺正洪,刘进忙.基于改进遗传算法的防空火力优化分配方法[J].火力控制与指挥,2004,29(3):81-84.

REN Shaowei, HE Zhenghong, LIU Jinmang. The optimized distribution Method of the anti-air fire based on the improved genetic algorithm[J]. Fire Control & Command Control,2004,29(3):81-84.

[9] 宋笔锋,刘晓东,等.作战飞机方案和关键技术的决策理论与方法[M].北京:国防工业出版社,2010:60-65.

SONG Bifeng, LIU Xiaodong, et al. Combat aircraft scheme and technology of decsion theory and method[M]. Beijng: National Defence Industry Press,2010:60-65.

[10] 王宏论.多机空战模拟系统研究[D].西安:西北工业大学,1995:25-35.

WANG Honglun. Research on simulation system of air combat[D]. Xi’an: Northwestern Polytechnical University,1995:25-35.

[11] 王强,丁全心,张安,等.多机协同对地攻击目标分配算法[J].系统工程与电子技术,2012,34(7):1400-1405.

WANG Qiang, DING Quanxin, ZHANG An, et al. Target allocation algorithm for multi-cooperative air-groubd attack[J]. Systems Engineering and Electronics,2012,34(7):1400-1405.

[12] 甄涛,王平均,张新民.地地导弹武器作战效能评估方法[M].北京:国防工业出版社,2005:52-54.

ZHEN Tao, WANG Pingjun, ZHANG Xinmin. Missile combat effectiveness evaluation method[M]. Beijng: National Defence Industry Press,2005:52-54.

[13] 曾国贵,姜长生.武装直升机空战关键技术问题研究[J].直升机技术,2002(3):29-32.

ZENG Guogui, JIANG Changsheng. Research of Key Technical Problems About Attack Helicopter Air-combat[J]. Helicopter Technique,2002(3):29-32.

[14] 梁旭,黄明.现代智能优化算法及其应用[M].北京:电子工业出版社,2012:35-43.

LIANG Xu, HUANG Ming. Modern intelligent optimization algorithm and application[M]. Beijing: Electronic Industry Press,2012:35-43.

[15] 史峰,王辉,等.MATLAB智能算法[M].北京:北京航空航天大学出版社,2011:69-70.

SHI Feng, WANG Hui. MATLAB intelligence algorithm[M]. Beijing: Beijing University of Aeronautics and Astronautics Press,2011:69-70.

[16] Zhao B, Guo C X, Cao Y J. A multiagent-based particle swarm optimization approach for optimal reactive power dispatch[J]. IEEE Transactions on Power Systems,2005,20(2):1070-1078.

Target Assignment of the Helicopter Fleet Based on Multiple Population Genetic Algorithm

ZHOU KaiJIANG WenzhiCHEN Dengan

(Naval Aeronautical and Astronautical University, Yantai264001)

A multiple population genetic algorithm(MPGA) was put forward for multi-helicopter cooperation target assignment problem. In the algorithm, adopting immigration operator and competition operator was applied so as to make the MPGA more suitable for multi-helicopter cooperation target assignment problem. Aiming at the shorting of premature and poor resulted from pure GA, the algorithm performance was enhance observably by enhancing interactive between individual and superior individual and achieve carrying out being in conjunction with of various populations evolution. The simulated results show that the MPGA algorithm can solve multi-helicopter cooperation target assignment effectively, which was simple, flexible and easy to implement and expand.

multi-helicopter cooperation, multiple population genetic algorithm, target assignment

2016年3月17日,

2016年4月21日

周凯,男,硕士研究生,研究方向:计算机应用。姜文志,男,教授,博士生导师,研究方向:计算机应用、武器装备与作战指挥一体化。陈邓安,男,副教授,研究方向:兵种战术指挥。

V271.4; TP202DOI:10.3969/j.issn.1672-9722.2016.09.015