基于Sugarscape的动态人工社会网络语言竞争模型*
李张强 毕贵红 王海瑞
(1.昆明理工大学信息工程与自动化学院 昆明 650500)(2.昆明理工大学电力工程学院 昆明 650500)
基于Sugarscape的动态人工社会网络语言竞争模型*
李张强1毕贵红2王海瑞1
(1.昆明理工大学信息工程与自动化学院昆明650500)(2.昆明理工大学电力工程学院昆明650500)
在Sugarscape人工社会模型的基础上提出了一个复杂agent网络人工社会模型。Sugarscape空间中有代表经济发展水平的资源分布及资源再生机制,空间资源禀赋的不同将空间分为不同区域,agent生活在Sugarscape空间中,可以模拟一个动态的人口生长社会,赋予agent社会半径,并利用社会半径在Sugarscape构建社会圈子网络。Sugarscape空间不同区域不同agent的语言地位根据区域人口居住格局和文化经济发展水平的不同可以改变。Sugarscape空间中的不同区域资源分布和再生方式也可以改变。这样模型可以初步模拟人口不同居住格局、不同人口流动和不同经济文化发展水平等条件下,语言竞争的态势和政策调控。
agent; Sugarscape; 人工社会; 社会圈子网络; 语言竞争
Class NumberTP393
1 引言
在中国,随着社会的发展,少数民族语言的多样性正在遭受严峻的考验。为拯救濒危语言,有必要对语言传播、竞争、调控的机理和动力学特性深入研究,以揭示语言衰退、消亡和共存的原因,进而寻求濒危语言保护和干预措施。
Abrams和Strogatz[1](2003)在Nature上发表的论文(AS模型)提出了一个简单的确定性系统动力学方程,用以描述在一个人群中两种语言竞争引起的语言使用模式变化情况。Patriarca和Leppänen[2](2004)、Kandler和Steele[3](2008)以及Patriarca和Heinsalu[4](2009)在AS模型基础上考虑了在异质地理环境上的人口扩散和增长影响。Mira和Paredes[5](2005)对AS模型作了存在双语者的扩展,Minett和Wang[6](2008)用稍微不同的方式在模型中引入了双语者模型,说明双语者的存在有利于语言保持与共存。从以上模型我们可以看出双语者、人口流动和空间的异质性相互影响能导致弱势语言和强势语言共存。语言竞争系统是复杂适应性系统(Beckner[7],2009),同时,人们在对话交流过程中形成了语言传播网络,传播网络与语言交流传播行为相互影响形成了语言的竞争与演化,所以语言竞争与演化本质上是语言在复杂网络上的传播问题。基于复杂agent网络的建模方法是语言竞争复杂系统动力学性质的另一类重要研究方法[8~12]。这些模型研究了小世界网络、无标度网络以及具有高聚类系数和度-度相关特征的社群结构网络对语言竞争的影响。
Hamill和Gilbert[14]给出了一种基于agent的社会圈子网络理论来构建具有多种实际社会网络统计特征的社会网络生成方法。Robert Axtell[13]提出了一个人工社会Sugarscape模型模拟动态的人口生长社会和社会资源的流动更新。本文在Sugarscape人工社会的基础上引入基于agent的社会圈子理论,构建一个复杂agent网络的动态人工社会语言竞争模型,其可以初步模拟人口不同居住格局、不同人口流动和不同经济发展水平等条件下,语言竞争的态势和政策调控。模型主要有以下特点: 1) 社会网络具有动态特性更加接近实际。agent个体具有性别属性和不同的社会交流圈子,能选择符合条件的异性组成家庭生育子女,且可动态移动及更新。 2) 语言地位能根据区域人口居住格局(杂居、分片聚居)和经济发展水平而改变,体现出在不同社会区域中同一语言可具有不同的语言地位。 3) 区域内及区域间的人口流动能多方面体现出人口流动对语言竞争传播的影响。
2 糖域社会圈子网络
2.1糖域(Sugarscape)模型
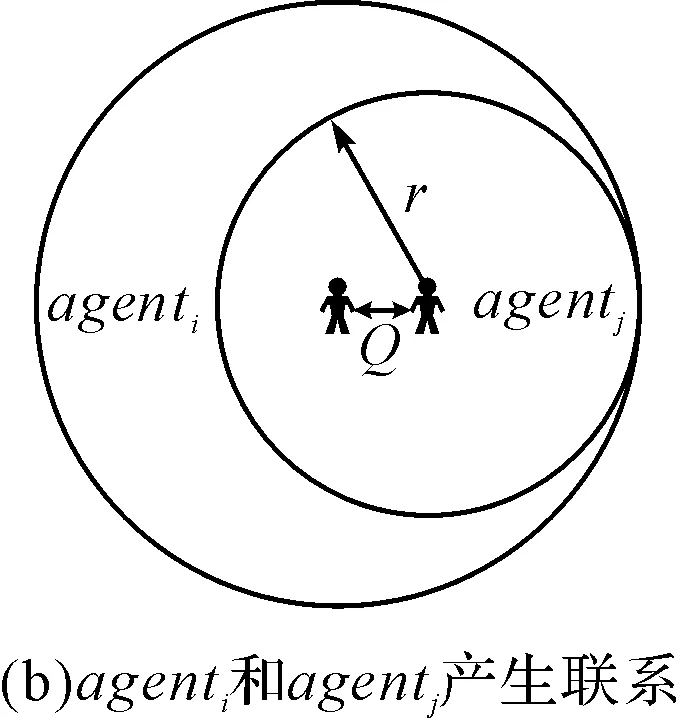
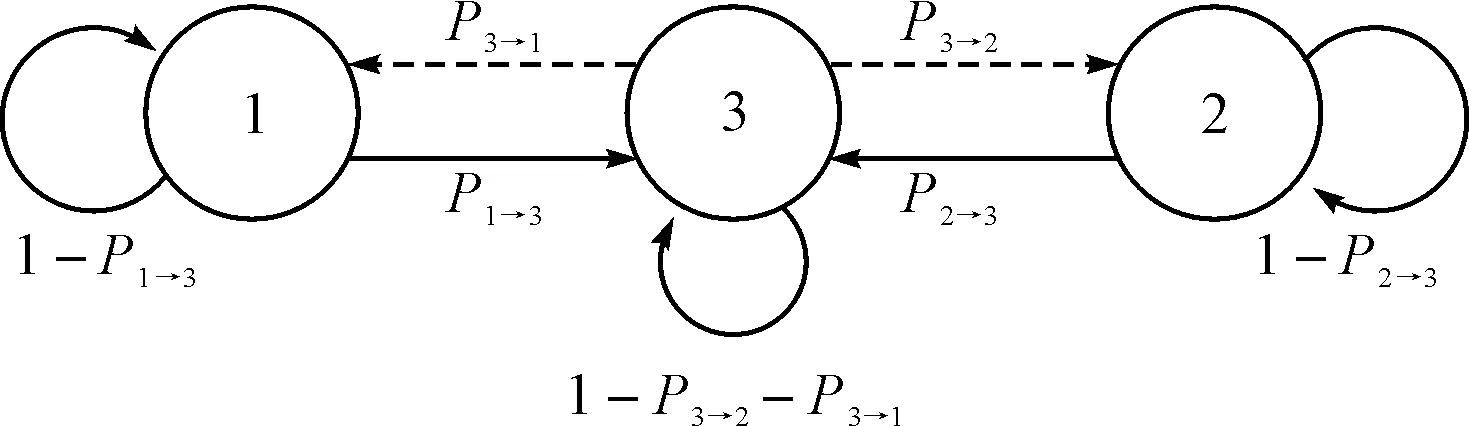
在Robert Axtell[13]提出的糖域(Sugarscape)模型中,有一个50×50个网格组成的二维仿真空间,空间中的每一个网格都有一个特定的坐标(x,y),坐标范围为-25 图1 糖量空间分布 如图1所示为本文所采用Sugarscape模型的两种糖量分布图,整个二维仿真空间按坐标y≥0或者y≤0分为上下对称的两个部分,上半部分为1区域,下半部分为2区域。 在语言竞争模型中,agent生活在这个二维空间中,并且能够自主地不断收集所在瓦片的糖资源,同时每个仿真周期内会进行新陈代谢从而消耗糖资源,当糖消耗完之后,agent个体就死去。本文中每一个网格位置,当糖被agent吸收后,立即恢复原有瓦片糖量。 2.2社会圈子网络模型 著名仿真学者Hamill[14]等提出一种基于agent的社会圈子网络理论来构建具有多种实际社会网络统计特征的社会网络生成方法。社会圈子网络模型中,个体拥有长度不等的社会交流半径,以个体自身为中心,社会半径长度为半径作圆形成个体的社会圈子,社会圈子大小的不同使个体交流范围产生差异。当两个体中心点的连线的长度Q小于等于连线两端个体较小社会半径r时,个体建立连接产生联系,图2(a)中Q>r,所以不产生联系;图2(b)中Q 如图3(a)杂居情况下初始时两种单语个体随机分布于整个仿真空间,图3(b)聚居情况下初始时单语1个体随机分布于1区域,单语2个体随机分布于2区域。 图3 社会圈子网络模型图 3.1双语竞争模型 3.1.1Castelló复杂agent网络语言竞争模型 (1) (2) 式(1)给出agenti从一种单语(A或B)变成双语AB的概率;式(2)反映agenti从双语到单语的转换概率。式中sA和sB表示单语A和单语B的语言地位,在一个拥有两种语言的社会中sA+sB=1;公式同时表明,两种单语间的转换需要通过双语AB过渡。 3.1.2V.Schwämmleagent有性别差异的语言竞争模型 在V.Schwämmle[16]提出的agent有性别差异的语言竞争模型中,用整数来表示语言的种类,分别是单语1、单语2以及双语3。产生后代的个体必须是两个性别相异的agent,父母的语言类型决定子代的语言类型,当父母语言类型一致时,子代的语言与父母语言一致;当父母的语言不一致时,引入了一个可调整的全局变量Pb(0≤Pb≤1)来表示产生双语后代的概率,如果产生的是单语子代,那么单语1和单语2的概率一样。 3.2动态agent网络语言竞争与演化 本文的语言竞争模型中,基于糖域模型并引入社会圈子网络,个体间语言传播和竞争模型借鉴Castelló[15]和V.Schwämmle[16]提出的模型。 3.2.1agent的属性 分布在二维世界中的仿真个体称之为agent,agent有很多自己的属性,agent的属性如表1所示。 表1 agent属性 图4 agent的视力范围 模型中agent在自己的视力(vision)范围内搜索符合规则的瓦片移动,agent能够在东西南北四个方向上看到vision个瓦片的范围。如图4所示,若vision=4,则agent能看到图中箭头方向的4个瓦片的范围。 二维仿真空间中,每个agent的社会圈子大小用社会半径societyRadial表示。现实社会中富有的人往往比贫穷的人社交范围更广,与之对应,将societyRadial分为三类:小社会半径(smallReach),中等社会半径(middleReach),大社会半径(bigReach)。 用areaiSj表示在i区域语言j的语言地位,混合杂居时area1S1=area2S1、area1S2=area2S2,并且area1S2+area2S1=1;分片聚居时不同区域内相同语言语言地位可能不同,但是在同一区域内两种单语的语言地位之和是1,即area1S1+area1S2=1,area2S1+area2S2=1。 3.2.2agent行为规则 agent的行为规则都是由糖域模型控制的,移动规则(MR)、繁殖规则(RR)、死亡规则(DR)、语言传播与竞争规则(TR)。 1) agent的移动规则(MR) 定义一个空的瓦片集合ps (1)以agent所在的瓦片为中心,agent的视力(vision)为范围,观察东南西北四个方向内的所有瓦片,如果这些瓦片中存在没被其它agent占据的空白瓦片,将这些空白瓦片放入集合ps中,并继续(2),否则agent不移动。 (2)在ps集合中取出糖量最大的瓦片,如果该瓦片的糖量值大于agent所在的瓦片糖量值,那么继续(1),否则不移动。 (3)agent移动到该瓦片。 (4)收集该瓦片的糖量,并更新agent糖量,即sugar=sugar+psugar。 2) agent的繁殖规则(RR) 本模型中,agent有性别属性,所以在仿真繁殖后代时模拟有性繁殖。 定义as为agent的一个集合,ps为一个瓦片集合。 (1)在已建立的社会圈子网络的基础上,遍历每个agent,如果agent有社会圈子,则进行(2),否则结束,不进行繁殖。 (2)对agent社会圈子中的其他个体,判断这些个体的性别,选中这些个体中和agent性别相反的个体,存入集合as,若as为空,则结束不进行繁殖,否则进行(3)。 (3)选取as任意一个agenti,判断agenti所在瓦片的东南西北四个方向的瓦片,判断其是否为空白瓦片,将不是空白的瓦片存入集合ps中。若ps为空,则结束,不进行繁殖。否则进行(4)。 (4)选取ps中的任意一个瓦片,在该瓦片上生成一个新的agent后代。 3) agent的死亡规则(DR) 在仿真模型中,agent的死亡主要两个属性确定,糖量(sugar)和年龄(age),当sugar≤0或者age>maxAge时,agent死亡。 在每个仿真周期遍历每个agent,判断其糖量(sugar)和年龄(age),以确定该agent死亡与否,同时随着agent的移动。更新所有agent的社会圈子网络,agent语言的传播和竞争发生在agent社会圈子内和agent产生后代的时候。 4) agent的语言传播与竞争规则(TR) 语言竞争模型中个体间的语言传播中语言转换和竞争借鉴Castelló[15]提出的式(1)、(2)以及V.Schwämmle[16]提出的模型中父母产生子代个体时的语言遗传方式,将语言的传播分为横向传播和纵向传播。横向传播就是agent个体之间通过社会圈子的联系,相互作用,从而agent的语言类型有可能发生转变。例如,在agenti的社会圈子中,agenti使用语言1,而在agenti的社会圈子网络中使用其他语言的agent占了大多数,agenti就可能学习另外一种单语,从而变成双语3,同样变成双语3的agenti也有可能因为社会圈子的原因而变成单语,称之为语言的遗忘。纵向传播就是在有性繁殖的agent产生后代时,父母辈agent通过自身的语言种类,影响子代的语言。 (1)agent语言的横向传播与竞争规则 社会圈子网络中的agent受到它所在社会圈子网络中其他agent个体的影响,而按一定的概率改变其语言状态行为称之为语言的横向传播。语言的横向传播分为语言学习和语言遗忘,单语者可能变成双语者,即1/2→3,称为语言学习;同理双语者可能变成单语者,即3→1/2,称为语言遗忘,双语3为agent语言转换的中间状态。如图5所示,为语言横向传播模型。 图5 语言横向传播模型 agent语言学习和语言遗忘的概率为P1→3、P2→3和P3→1、P3→2,仿真时判断一个agent是否进行语言学习或者语言遗忘,是通过编程产生一个0~1之间的随机浮点数和P3→2、P2→3、P3→1、P3→2的对比结果决定。当P3→2、P2→3、P3→1、P3→2大于随机产生的随机浮点数时,agent进行语言学习或语言遗忘。P3→2、P2→3、P3→1、P3→2的计算公式如下。 在1区域单语个体发生语言学习变成双语者和双语个体发生语言遗忘变成单语者的概率计算公式如下: P1→3=area1S2×σ2P2→3=area1S1×σ1 (3) P3→1=area1S1×(σ1+σ3) P3→2=area1S2×(σ2+σ3) (4) 在2区域单语个体发生语言学习变成双语者和双语个体发生语言遗忘变成单语者的概率计算公式如下: P1→3=area2S2×σ2P2→3=area2S1×σ1 (5) P3→1=area2S1×(σ1+σ3) P3→2=area2S2×(σ2+σ3) (6) 式中agent个体σ的计算,设agent所在社会圈子中其他agent的总数为n,使用语言1的单语者数量为n1,使用语言2的单语者数量为n2,使用双语3的人数为n3=n-n1-n2,则有: σ1=n1/nσ2=n2/nσ3=1-(σ1+σ2) (7) 当两个单语发生竞争,弱势的单语向强势单语转变时,如1→2时,不会发生直接转变,而是通过语言学习成为双语者3,而后通过语言遗忘过程遗忘单语1,即1→3→2。 语言横向传播模型的特点如下:(1 agent个体语言状态的改变受它的语言地位和所在社会圈子其他agent的影响;(2)语言的学习只发生在单语者身上,语言的遗忘只发生在双语者身上。 (2)Agent语言的纵向传播和竞争规则 父母辈的语言类型决定子代的语言类型称为语言的纵向传播,模型中提出语言的纵向传播和竞争规则借鉴了V.Schwämmle[16]提出的模型中父母产生子代个体时的语言遗传情况,①父母双方的语言相同,那么子代的语言一定和父辈相同,②父母双方的语言不一样,引入了产生双语后代的概率Pb,Pb在仿真模拟时设置成一个可调节的全局变量,当产生单语后代时,在V.Schwämmle[16]的模型中,产生单语1后代和单语2后代的概率一样,但在本文中,这种情况下产生单语1后代或者单语2后代的概率和单语1和单语2在该区域的语言地位正相关。 本模型以Netlogo[17]为平台,agent所处的仿真环境设定为50×50(2500个单元网格)的二维网格空间,在提出的基于Sugarscape社会圈子语言传播网络模型中,个体的移动、出生、死亡等行为规则都是基于Sugarscape,模型中分别仿真实现了混合杂居和分片聚居情况下双语的竞争。具体如表2所示。 4.1混合杂居情况语言地位对双语竞争的影响 如图6所示,为混合杂居情况下仿真参数为初始值时与改变语言地位至area1S1=area2S1=0.45、area1S2=area2S2=0.55,其他参数与初始值相同时,仿真演化版图和语言人口比例图。初始时单语1在全局的语言地位为0.4,单语2在全局的语言地位为0.6,此时单语2为强势语言,单语1为弱势语言。改变语言地位后,单语2仍然是强势语言,单语1为弱势语言,但是相比初始时,单语1语言地位从0.4增加到0.45,单语2语言地位从0.6减少到0.55。从图7可以看出,初始时候强势语言单语2迅速增加,并成为全局的主流语言,弱势语言单语1在总人口中占的比例迅速减少,并最终基本消亡,而作为中间状态的双语3随着单语1的减少而减少,在单语1消亡后也迅速消亡。改变语言地位后,强势语言单语2的增加速度和弱势语言单语1的减少速度都降低了,在全局形成单语2个体占大部分,单语1和双语3个体占小部分,并且单语1和单语2共存的局面。即在实际社会生活中,提高弱势语言的语言地位,便会提高该语言在经济、政治和文化方面的地位,增强持该种语言的自豪感,有利于保护弱势语言。 表2 仿真参数初始值 图6 杂居情况下改变语言地位人口比例对比图 4.2混合杂居情况双语后代遗传率Pb和个体社会半径对双语竞争的影响 如图7所示,为双语后代遗传率Pb和个体社会半径不同时语言人口比例对比图,情况一Pb=0.3、societyRadial分别为1、2、3,情况二Pb=0.35、societyRadial分别为1、2、2,两种情况下两种语言地位相同,单语1语言地位为0.45,单语2语言地位为0.55,其他参数值与表2中的仿真参数初始值相同。从图中可以看出,两种情况下两种语言都能共存,但是对比两种情况下两种语言的人口比例图,情况二更有利于弱势语言的生存,而情况一相对更有利于强势语言,即提高双语后代和减小个体的社会半径更有利于弱势语言的保护。在现实社会生活中,让更多的强势语言个体学习弱势语言,增加社会网络中双语人口的比例和个体相对小的社会交际圈子更有利于保护弱势语言。 图7 杂居情况改变遗传率和社会半径人口比例对比图 4.3混合杂居和分片聚居对双语竞争的影响 如图8所示,分别为参数值与表2中的仿真参数初始值相同时混合杂居和分片聚居仿真演化版图和语言人口比例对比图。仿真参数初始时,单语1为弱势语言,单语2为强势语言,所以结合两个图可以看出两种情况下,单语1个体总是随着仿真的进行越来越少,单语2个体则相反,但是在分片聚居的情况下弱势语言单语1个体减少的速度对比杂居情况更小,在现实社会中很容易找到例子,例如少数民族聚居地的少数民族语言总是能得到较好的保存和使用。 图8 杂居和聚居人口比例对比图 4.4分片聚居情况语言地位对双语竞争的影响 如图9所示,为在分片聚居的情况下仿真参数为表2中的仿真参数初始值和改变语言地位至area1S1=0.6、area2S1=0.4、area1S2=0.4、area2S2=0.6语言人口比例对比图。从图中可以看到改变语言地位后单语1和单语2可以很好的共存,并且两种语言的人口数相当。改变语言地位后,在仿真二维空间的上半部分即1区域,单语1为强势语言,在仿真二维空间的下半部分2区域,单语2为强势语言,在两种语言的各自区域形成优势语言区,由于语言地位的差异,外来语言人口进入该区域后,很容易被同化,这样就形成内向型社会,很好地保护了当地区域的语言。 图9 分片聚居情况改变语言地位人口比例对比图 根据仿真实验的结果,可以提出保护弱势语言的建议: 1) 语言地位对语言保护至关重要。在当前社会经济环境下,少数民族人员的母语和保护意识需要从以前的不自觉变为自觉,需要通过教育宣传措施增强语言和文化的自豪感和自信心。 2) 大力发展弱势语言区域的经济、加强基础公共设施的建设,为人们提供更好的服务,使得区域内的个体对母语的自豪感和自信心大大增强。 3) 分片聚居比混合杂居更有利于弱势语言的保护,可以考虑形成弱势语言聚居区。 4) 如果形成杂居的情况,建议在强势的单语个体中普及弱势语言,增加双语人口的比例。 5) 现代社会中个体的流动和交流大大增加不利于保护弱势语言,可以从个体的流动方面考虑保护弱势语言。 [1] Abrams D M, Strogatz S H. Modeling the dynamics of language death[J]. Nature,2003,424:900. [2] PATRIARCA M, LEPPNEN T. Modeling language competition[J]. Physica A: Statistical Mechanics and its Applications,2004,338(1):296-299. [3] KANDLER A, STEELE J. Ecological models of language competition[J]. Journal of Biological Theory,2008,3(2):164-173. [4] Patriarca M, Heinsalu E. Influence of geography on language competition[J]. Physica A: Statistical Mechanics and its Applications,2009,388(2-3):174-186. [5] Mira J, Paredes A. Interlinguistic similarity and language death dynamics[J]. Europhysics Letters,2005,69(6):1031-1034. [6] Minett J W, Wang W S Y. Modeling endangered languages: The effects of bilingualism and social structure[J]. Lingua,2008,118(1):19-45. [7] Beckner C, et al. Language is a Complex Adaptive System: Position Paper[J]. Language Learning,2009,59(S1):1-26. [8] Stauffer D, Castelló X, Eguíluz V M, et al. Microscopic Abrams-Strogatz model of language competition[J]. Physica A: Statistical Mechanics and its Applications,2007,374(2):835-842. [9] Castelló X, Eguíluz V M, Miguel M S. Ordering dynamics with two non-excluding options: bilingualism in language competition[J]. New Journal of Physics,2006,8(12):308-322. [10] Li X, Chen G. A local-world evolving network model[J]. Physica A: Statistical Mechanics and its Applications,2003,328(1-2):274-286. [11] Castelló X, Toivonen R, Eguiluz V M, et al. Anomalous lifetime distributions and topological traps in ordering dynamics[J]. Europhysics Letters,2007,79(9):66006(1-6). [12] Toivonen R, Castelló X, Eguiluz V M, et al. Broad lifetime distributions for ordering dynamics in complex networks[J]. Physical Review E,2008,79(1):016109. [13] Eptein J M, Axtell R. Growing artificial societies, social science from the bottom up[M]. Washington, D. C.: Brookings Institution Press; Cambridge, Mass.: MIT Press,1996. [14] Hamill L, Gilbert N. Social Circles: A Simple structure for Agent-Based social network models[J]. Journal of Artificial Societies and Social Simulation,2009,12(23):3-20. [15] Xavier Castelló, Víctor M. Eguíluz, Maxi San Miguel. dynamics of language competition: effects of bilingualism and social structure[J]. New Journal of Physics,2007,6(10):111-302. [16] V. Schwämmle. Simulation for competition of languages with an ageing sexual population[J]. International Journal of Modern Physics C,2008,9. [17] WILENSKY U. (1999) NetLogo.Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL, USA.[Z/OL].(2012)[2012].http://ccl.northwestern.edu/netlogo/. Language Competition Model with Dynamic Artificial Social Network Based on Sugarscape LI Zhangqiang1BI Guihong2WANG Hairui1 (1. College of Information Engineering and Automation, Kunming University of Science and Technology, Kunming650500) (2. College of Electric Power Engineering, Kunming University of Science and Technology, Kunming650500) This paper proposes a complex agent network artificial social model based on Sugarscape artificial social model. The distribution of resource in the Sugarscape space stand for the level of economic development and Sugarscape provides the rule of resource regeneration. The simulation space could be divided into two different area by the different resource of Sugarscape space. Agent lives in Sugarscape space to simulates a dynamic growing artificial society. Every agent has social radius and builds its social circle network by social radius in Sugarscape. Agents’ language may change its status because of the different living situations and the different levels of economic development. The distribution of resource and the rule of resource regeneration could be different in different Sugarscape areas. In this way the model could move on to the simulation of language competition under different agent living situation, different migration movements and different levels of economic cultural development and according to the results of simulation to get some policies in protecting endangered language. agent, Sugarscape, artificial society, social circle network, language competition 2016年3月30日, 2016年4月30日 国家自然科学基金项目(编号:61364022)资助。 李张强,男,硕士研究生,研究方向:复杂系统与复杂网络建模仿真。毕贵红,男,博士,教授,研究方向:社会与经济系统仿真。王海瑞,男,博士,教授,研究方向:计算机智能控制。 TP393DOI:10.3969/j.issn.1672-9722.2016.09.018


3 基于Sugarscape社会圈子网络的语言竞争模型



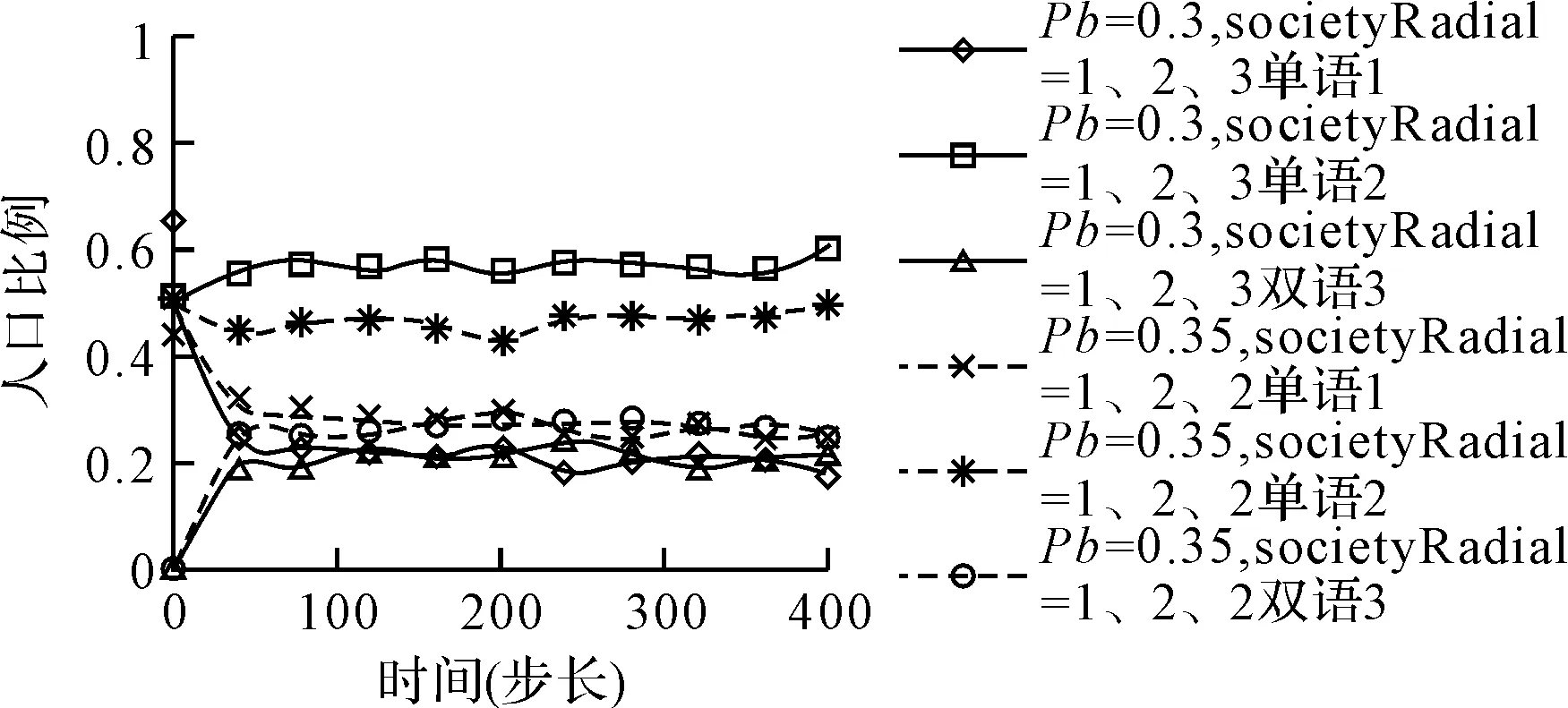
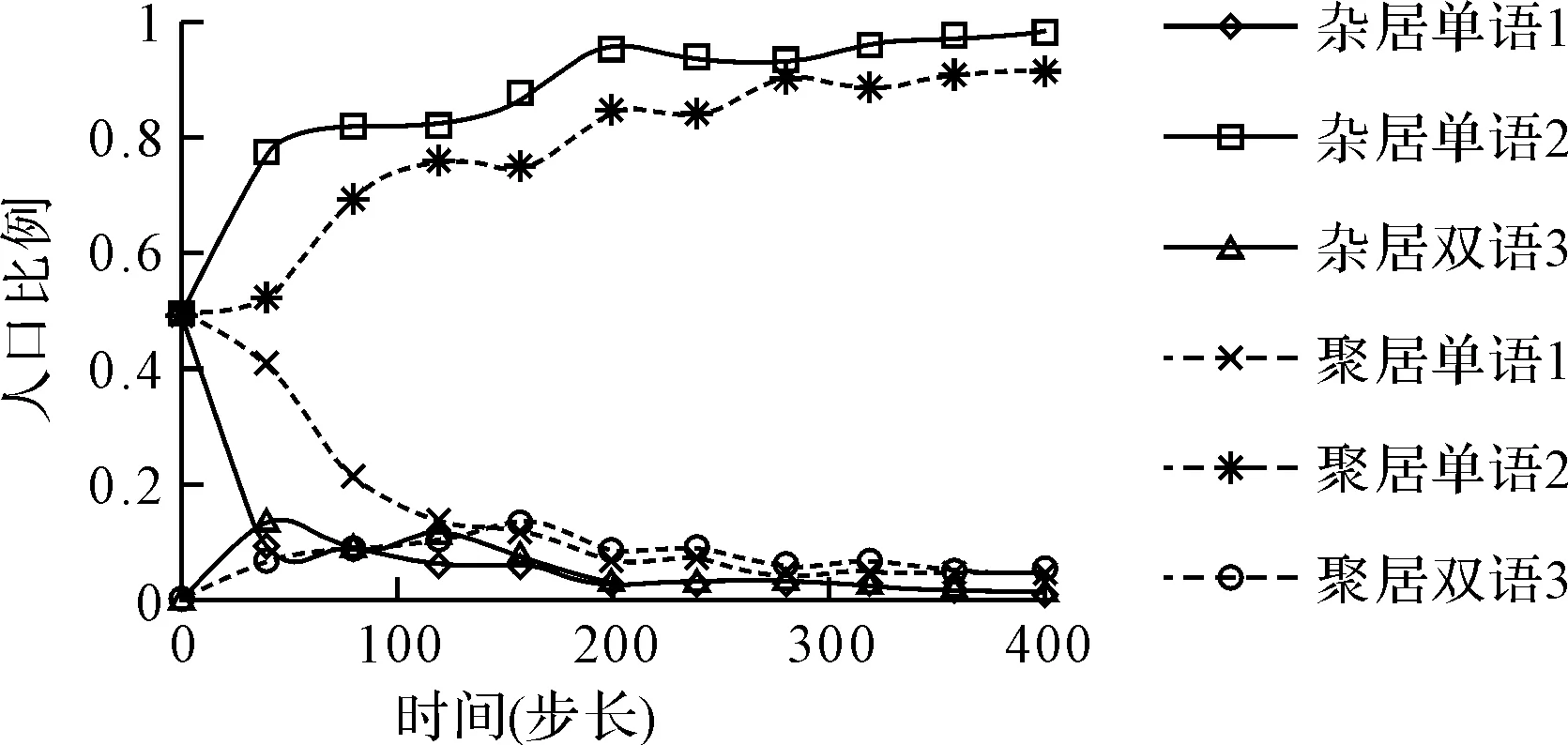
4 仿真结果分析



5 结语

