蚁群算法在旅行商问题(TSP)中的应用研究*

贾燕花

(山西工程职业技术学院　太原　030009)



蚁群算法在旅行商问题(TSP)中的应用研究*

贾燕花

(山西工程职业技术学院太原030009)

旅行商问题(TSP)是组合优化领域里的一个典型的、易于描述却难以处理的NP完全难题,其可能的路径数目与城市数目是呈指数型增长的,求解非常困难。蚁群算法是近年来新出现的一种随机型搜索寻优算法,已引起越来越多的关注和重视,论文进一步将这种新型的生物优化思想运用到旅行商问题(TSP)中,并给出用蚁群算法求解TSP,获得了较满意的效果。

蚁群算法P; 组合优化; TSP

Class NumberTP301

1　引言

受到自然界中真实蚂蚁集体行动的启发,意大利学者M.Dorigo于1991年在他的博士论文中首次提出了一种基于蚂蚁种群的新型优化算法——蚁群算法。并用该方法解决了一系列组合优化问题。蚁群算法在解决这类问题中取得了一系列较好的实验结果。旅行商问题(TSP)即给定n个城市之间的距离,要求确定一条经过各城市当且仅当一次的最短路线,这类似于生物界的蚂蚁的觅食行为。根据昆虫学家的观察和发现,蚂蚁从蚁穴出发到达食物地寻找食物时,会在没有任何提示下找出从蚁穴到食物源的最短路径,并且能随环境的变化而变化地搜索新的路径,产生新的选择路径的方法。蚂蚁能在其走过的路径上释放一种蚂蚁特有的分泌物——信息素[4](外激素),使一定范围内其他的蚂蚁能觉察到并由此影响它们以后的行为,当一些路径上的蚂蚁越来越来多时,其留下的信息素轨迹也越来越多,以致信息素强度增大,但随时间的推移会逐渐减弱,后来蚂蚁选择该路径的概率也越高,从而更增加了该路径的信息素强度,这种选择过程被称之为蚂蚁的自催化行为,其原理是一种正反馈机制。本文运用蚁群算法求解著名的旅行商问题,从实验上探索了优化能力,获得了满意的效果。

2　蚁群算法模型的建立[5]

在蚁群优化算法中,一个有限规模的人工蚁群体[6],可以相互协作地搜索用于解决优化问题的较优解。人工蚁群算法的基本原理吸收了生物界中蚂蚁群体的某些显著的特征: 1) 能觉察小范围区域内状况并判断出是否有食物或者信息素轨迹; 2) 能释放自己的信息素; 3) 遗留在路径上的信息素并不会一直存留,而是会随时间逐渐减少。由于生物界中的蚂蚁的视觉信号很弱,基本没有视觉,所以它们并不是靠观察去寻找食物,而是靠它们的伙伴释放在周围环境中的信息素来决定自己去何处寻找食物。尽管没有先验知识,但是蚂蚁还是有能力找到从蚁穴到食物源的最短路径[7](最佳路径),甚至在该路径上放置障碍物后,它们仍然能很快重新找到最佳路径[8～9]。图1、图2为蚂蚁觅食时寻找最佳路径的分析图。

图1　蚁群在等距离路径上寻找最佳路径

图2　蚁群在非等距离路径上寻找最佳路径

在图1中AB、BD、AC、CD均等距离,为了方便实验均取值为1,而图2中,另AB、BD均取为1,而AC、CD均取为2,两图中从蚁穴到A点的距离,D点到食物源的距离均为1。在图1中,两个分支上最初没有信息素,因此蚂蚁选择两个分支的概率是相同的,然而,经过最初一个短振荡阶段,随机的振荡使得更多的蚂蚁随机地选择了其中一个分支。而对于图2中蚂蚁选择路径时就复杂一些了,开始两个分支上都没有信息素,所以蚂蚁随机地选择一条路径,有20只蚂蚁从蚁穴出发,当走A点时,按照概率相同的原则,有10只蚂蚁选择了左边的分支,另外10只蚂蚁选择了右边的分支,但是过一段时间后,蚂蚁并不会像图1中的蚂蚁那样经过振荡后随机选择其中一条路径,而是有目的地选择了路径,原因是路径上信息素的多少发生了改变,其中短路径的一条会比长路径的一条早聚集信息素,使得以后的蚂蚁会“有意识”地选择短路径(最佳路径)。图2分析如下:

在t=0时刻,20只蚂蚁从蚁穴出发移动到A,它们以相同概率选择左侧或右侧道路,因此平均有10只蚂蚁走左侧,10只走右侧;

在t=4时刻,第一组到达食物源的蚂蚁将折回;

在t=5时刻,两组蚂蚁将在D点相遇,此时BD上的信息素数量与CD上的相同,因为各有10只蚂蚁选择了相应的道路,从而有5只返回的蚂蚁将选择BD而另5只将选择CD;

在t=8时刻,前5个蚂蚁将返回巢穴,而AC、CD和BD上各有5个蚂蚁;

在t=9时刻,前5个蚂蚁又回到A并且再次面对往左还是往右的选择;

这时,AB上的轨迹数是20,而AC上是15,因此将有较为多数的蚂蚁选择往左,从而增强了该路线的信息素。随着该过程的继续,两条道路上信息素数量的差距将越来越大,直至绝大多数蚂蚁都选择了最短的路线。正是由于一条道路要比另一条道路短,因此,在相同的时间区间内,短的路线会有更多的机会被选择。

3　蚁群算法求解TSP

3.1相关定义

用蚁群算法求解TSP时,首先要模拟实际蚂蚁的行为,引入如下记号:

·m为蚁群中蚂蚁数量;

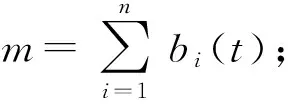
·dij为两个城市i和j之间的距离;

·ηij为边(i,j)的能见度,反映由城市i到城市j的启发程度,这个量在蚂蚁系统的运行中不改变;

·τij为边(i,j)上的信息素轨迹强度;

·Δτij为蚂蚁k在边(i,j)上留下的单位长度轨迹信息素;

·Q为蚂蚁在路径上留下轨迹数量的一个常数。

每只蚂蚁都是具有如下特征的简单主体:

1) 在从城市I到城市j的运动过程中或是在完成一次循环后,蚂蚁在边(i,j)上释放一种物质,称为信息素轨迹;

2) 蚂蚁概率地选择下一个将要访问的城市,这个概率是两个城市间距离和连接两城市的路径上存有轨迹量的函数,在t时刻,蚂蚁k在城市I选择城市j的转移概率为

其中,α为轨迹的相对重要性(α≥0);β为能见度的相对重要性(β≥0)。

3) 为了满足问题的约束条件,在完成一次循环以前,不允许蚂蚁选择已经访问过的城市。

3.3蚁群算法实现过程

蚁群算法实现过程如下:

在地球上打洞，是为了缩短从地球的一端到达另一端的时间。最简单的模型，即在地球两极之间开一个洞，让物体自由的掉落进去。但即便如此，也可以使运输时间从原先漫长的十几个小时缩短到短短四十多分钟。我们首先对其进行简单的研究。

1) 初始化:nc←0;(nc为迭代数)τij←0;Δτij←0;

2) 将每只蚂蚁放置到一个起始结点上,即城市上,取蚂蚁数m与城市数n相等,并将各蚂蚁的当前所在的结点放置到禁忌表中,每当蚂蚁访问完一个城市时就将该城市放到此表中,以防蚂蚁再次访问;

3) 对每个蚂蚁应用一个状态转移规则来建立一个问题的解决方案,并应用局部信息素更新规则;

4) 计算各个蚂蚁的目标函数值;

5) 到所有的蚂蚁都建立了完整的解决方案;

6) 应用全局信息素更新规则,按照预先定义了的更新方程修改轨迹强度;

7) 若nc<预定义的迭代次数且无退化行为,则转入2),直到满足条件为止。

流程图如图3所示。

图3　蚁群算法流程图

4　实验结果分析

在Matlab环境下进行仿真实验,城市数取为31(我国省会城市个数)进化代数取10次实验结果的平均值,得到如下仿真图4、图5所示。

5　结语

做为一种全局搜索算法,蚁群算法能够有效地避免局部极优,但是这种算法的时间开销也会增加,尤其是对于大空间的多点全局搜索[11],却不可避免地增加搜索所需要的时间。为了使算法能够更好更快地找到问题的最优解,在实际算法过程中加入针对具体问题的局部搜索算法不失为一种好的选择。利用蚁群算法的全局性避开了局部极优,利用局部搜索算法加快了求解的过程,寻求二者的完善结合的更好的算法值得进一步研究。另外,和其他仿生算法的结合,形成混合仿生算法模型,也会使求解问题变得更加有效。

图4　最优路径线路

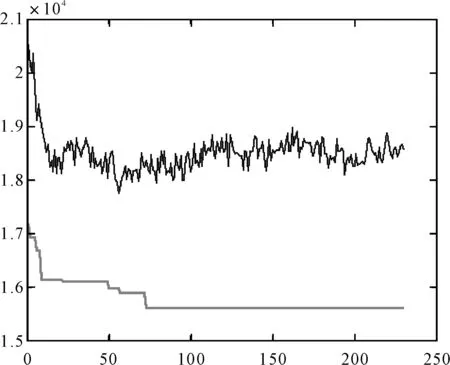
图5　最优路径长度

[1] 夏小云,周育人.蚁群优化算法的理论研究进展[J].智能系统学报,2016,11(1):27-36.

XIA Xiaoyun, ZHOU Yuren. Advances in theoretical research of ant colony optimization[J]. CAAI Transactions on Intelligent Systems,2016,11(1):27-36.

[2] 秦全德,程适,李丽,等.人工蜂群算法研究综述[J].智能系统学报,2014,9(2):127-135.

QIN Quande, CHENG Shi, LI Li, et al. Artificial bee colony algorithm: a survey[J]. CAAI Transactions on Intelligent Systems,2014,9(2):127-135.

[3] 曹金保.人工蜂群算法研究综述[J].电子设计工程,2012,21(23):35-38.

CAO Jinbao. Overview of research on artificial bee colony algorithms[J]. Electronic Design Engineering,2012,21(23):35-38.

[4] 俞庆生,林冬梅,王东.多旅行商问题研究综述[J].价值工程,2012(2):166-167.

YU Qingsheng, LIN Dongmei, WANG Dong. An Overview of Multiple Traveling Salesman Problem[J] . Value Engineering,2012(2):166-167.

[5] 孙力娟,王良俊,王汝传.改进的蚁群算法及其在TSP中的应用研究[J].通信学报,2004,25(10):112-116.

SUN Lijuan, WANG Liangjun, WANG Ruchuan. Research of using an improved ant colony algorithm to solve TSP[J]. Journal of China Institute of Communications,2004,25(10):112-116.

[6] 田晓辉.蚁群算法理论及其应用研究[J].科技信息,2012(33):487-518.

TIAN Xiaohui. The Research and Applicalion of Ant Colony Algoritlma[J]. Science & Technology Information,2012(33):487-518.

[7] 刘彦鹏.蚁群优化算法理论研究及其应用[D].杭州:浙江大学,2007:15-41.

LIU Yanpeng. Research on Ant Colony Optimization and Its Application[D]. Hangzhou: Zhejiang University,2007:15-41.

[8] 陈文兰,戴树贵.旅行商问题算法研究综述[J].滁州学院学报,2006,8(3):1-5

CHEN Wenlan, DAI Shugui. An Overview of Traveling Salesman Problem[J]. Journal of Chuzhou University,2006,8(3):1-5.

[9] 黄翰,郝志峰,吴春国,等.蚁群算法的收敛速度分析[J].计算机学报,2007,30(8):1344-1353.

HUANG Han, HAO Zhifeng, WU Chunguo, et al. Heconvergence speed of ant colony optimization[J]. Chinese Journal of Computers,2007,30(8):1344-1353.

[10] 宋锦娟.一种改进的蚁群算法及其在最短路径问题中的应用[D].太原:中北大学,2013:16-30.

SONG Jinjuan. An Improved Ant Colony Algorithm and Its Application in Optimal Routing Problem[D]. Taiyuan: North University of China,2013:16-30.

[11] 魏赟,陈元元.基于改进蚁群算法的云计算任务调度模型[J].计算机工程,2015,41(2):12-16.WEI Yun, CHEN Yuanyuan. Cloud Computing Task Scheduling Model Based on Improved Ant Colony Algorithm[J]. Computer Engineering,2015,41(2):12-16.

Application of the Ant Algorithm in TSP

JIA Yanhua

(Shanxi Engineering Vocational College, Taiyuan030009)

The traveling salesman problem(TSP) is one of the typical NP-Complete hard problems in combinatorial optimization, which is easy to be described but hard to be solved. The number of possible paths increase exponentially with the number of cities, the solution is very hard. Ant algorithm is a newly emerged stochastic seaching optimization algorithm in recent years. It has been paid much attention to. This paper solves the TSP with this new biological optimization strategy and gives the proceses of ant algorithm. And the satisfied effect is obtained.

ant algorithm, combinatorial, TSP

2016年3月11日,

2016年4月20日

贾燕花,女,硕士,网络工程师,研究方向:计算机网络管理和研究。

TP301DOI:10.3969/j.issn.1672-9722.2016.09.008