一种新的基于自适应窗口的压缩跟踪算法*

汪　龙

(南昌航空大学　南昌　330063)



一种新的基于自适应窗口的压缩跟踪算法*

汪龙

(南昌航空大学南昌330063)

论文提出了一种新的自适应窗口调整的方法,首先提取每帧图像目标在跟踪框内的灰度值,计算其灰度均值,然后比较相邻两帧图像的灰度均值,通过其比值建立了一种自适应窗口尺度调整的数学模型,最后与压缩跟踪算法结合起来对尺度变化的目标进行跟踪。解决了压缩跟踪算法中跟踪窗口不能随目标大小而改变这一问题。从而使压缩跟踪算法在目标尺度发生变化时,及时调整跟踪窗口的尺度,从而提高跟踪精度。实验结果表明,改进后的算法比压缩跟踪算法具有更好的鲁棒性,跟踪性能得到提升。

压缩跟踪; 灰度均值; 自适应窗口

Class NumberTP301.6

1　引言

目标跟踪,旨在估计视频序列中目标的位置,在视觉领域是个挑战性难题。在很多应用里起着至关重要的作用,尤其是在人机交互,视频监控、运动分析,图像压缩以及运动识别领域。过去几年目标跟踪取得了巨大进步,然而由于要考虑到目标的外观变化,如何对视频序列中的目标进行有效的跟踪是计算机视觉中一个有挑战性的课题。

压缩感知最早由Candes和Donoho于2006年提出[1～2],依据原信号稀疏特性,以远小于Nyqusit频率的随机采样获取原信号离散样本,通过非线性重构算法构造出具有原信号特性的降维信号。压缩感知算法被广泛地应用于图像处理极其应用当中[3]。2012年前后,压缩感知算法被引入目标跟踪上[3,5],通过剔除图像特征中冗余信息,利用稀疏的投影矩阵直接对特征信号进行抽样和压缩,对压缩特征进行分类,寻找出目标的最优估计,算法的计算量小,鲁棒性较高。文献[4]将目标和背景划分为正负样本集,在投影矩阵中尽可能寻找正样本所对应的投影系数最大候选位置,但投影矩阵难以精确确定,当目标运动过快时,跟踪窗偏离甚至脱靶。文献[5](Compressive Tracking)即压缩跟踪算法寻找一个宽松规则生成稀疏投影矩阵,将压缩后的数据作为特征来进行分类,优点是简单、高效,但该算法依然存在一些缺陷。

压缩跟踪算法(CT)的跟踪窗口在跟踪过程中保持不变,但是目标的大小显然并不是固定不变的。当目标变大时,负样本的采集太靠近目标区域,使得背景和目标的可区分度降低;当目标变小时,更是有部分背景信息被引入到参数模型中,从而导致跟踪漂移,甚至是跟踪失败。提出一种自适应窗口调整的方法,在压缩感知跟踪算法的基础上,建立了一种自适应窗口尺度调整的数学模型,当目标尺度发生变化时,及时调整跟踪窗口的尺度,从而提高跟踪精度。

2　压缩跟踪算法简介

压缩感知跟踪算法包括两部分,基于压缩感知的特征提取和基于贝叶斯分类器的目标检测。

2.1基于压缩感知的特征提取

压缩跟踪算法的特征提取是一种基于压缩感知理论[1,6]的特征提取。压缩感知理论指出,对于高维图像空间中的数据x∈Rn要将其投影到低维空间v∈Rn,可以使用随机矩阵R=Rn×m即

v=Rx

(1)

其中n≪m。理想情况下,希望矩阵R能够大致保持原信号点对之间距离。Johnson-Lindenstrauss推论[7]指出,如果向量空间中的两点投影到一个随机选择的合适的高维子空间,那么它们之间的距离得以保持的概率很高。Baraniuk等[8]证明了随机矩阵满足Johnson-Lindenstrauss推论,且在压缩感知领域中同样满足等距性质。因此,如果式(1)中的随机矩阵满足Johnson-Lindenstrauss推论,且信号x是可压缩的(如音频或者图像),那么可以有较高的概率从向量v中以最小误差来重建x。可以确保,向量v几乎保存了向量x的所有信息。该理论使得通过低维随机投影信号来分析高维信号成为现实。压缩跟踪算法使用的随机矩阵是一个稀疏矩阵,该矩阵不但满足Johnson-Lindenstrauss推论,而且可以在实时跟踪中进行有效地计算。其生成规则为:

(2)

式中p代表ri,j取某值的概率,压缩跟踪算法中设定s=m/4。分析可知,在满足Johnson-Lindenstrauss推论的前提下,当压缩矩阵中ri,j=0的概率越大时,所能避免的计算就越多、存储量的要求也越低。

压缩跟踪算法实际上使用的是与Haar-like特征[9～10]相似的相对强度差异特征。对于每一个采集到的样本,经过多尺度平滑滤波(矩形滤波器)后,连接在一起,生成一个高维多尺度图像特征向量(即各图像按照尺度大小、左右、上下顺序将像素连接在一起)。对于这样的高维(维数可达到106～1010)使用稀疏随机矩阵将其投影到低维中去。

2.2基于贝叶斯分类器的目标检测

后续的跟踪是在图像序列中迭代寻找出与标准目标特征最相似的候选区域。即以当前帧目标区域(以跟踪窗为准)邻近区域为候选区域,完成对其遍历,迭代计算出其与目标区域的相似性程度,相似程度最高的候选区域作为下一帧的目标区域。压缩感知跟踪算法以贝叶斯准则作为相似性判据,并假设所有特征相互独立。

在采样过程中将趋于目标的样本视为正样本并保留,远离目标的样本视为负样本,并舍去,则对于每一个样本z∈Rm,它的低维度表示是v=(v1,…,vn)T∈Rn,mn。假定在v中的每一个元素都是独立分布的,采用一个朴素贝叶斯分类器[10]创建它。

(3)

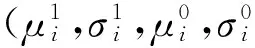
(4)

计算出当前帧中H(v)最大的候选区域作为下一帧的目标区域,并对相关系数进行更新

(5)

3　基于自适应窗口的压缩跟踪算法

压缩跟踪算法不能处理目标尺寸的问题,即目标跟踪窗口的大小保持不变。通过分析可知,这种算法在目标变大时影响负样本的采集,在变小时影响正样本的采集,而分类器的模型参数正是通过对正负样本的计算得到。所以,为了避免由目标尺度变化带来的跟踪漂移问题,本文提出一种自适应窗口调整的方法,在压缩跟踪算法的基础上,建立了一种自适应窗口尺度调整的数学模型,当目标尺度发生变化时,及时调整跟踪窗口的尺度,适应目标的变化。

图1

如图1所示预先定义好定义第K帧中的目标跟踪窗口宽度和高度分别为w和h。则运动目标在第K+1帧中尺寸可能会出现变大不变和变小三种情况。在运动目标变大时,尺寸可以定义为(Wb,Hb);在运动目标变小时尺寸可以定义为(Ws,Hs),第K帧和K+1帧之间宽度和高度调整尺寸为Sw和Sh。

为了确定目标尺寸变化,可以通过分析比较目标灰度均值的变化,在跟踪窗口尺度不变的情况下,则当实际目标尺寸增加时,灰度均值会增大会变大;相反,若目标尺度变小,则灰度值也会减小,假设在跟踪框不变的情况下设第K帧时跟踪框内的目标灰度均值为Kag,第K+1帧目标灰度均值为K+1ag。

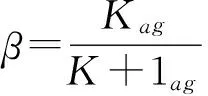
(6)

整体算法流程如下:第K帧图像目标位置lk和跟踪框尺度(w,h),对于K+1帧图像

1) 提取目标lk位置目标跟踪框(w,h)尺度内的灰度均值Kag;

2) 在K帧图像目标位置lk采集一系列的候选目标图集并在低维空间提取它们的特征值v(z);

3) 使用分类器对这些候选目标图集的低维特征进行分类,通过最大分类响应来找到K+1帧图像的目标位置lk+1,在该位置提取目标跟踪框(w,h)尺度内的灰度均值K+1ag;

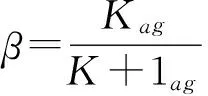
5) 根据式(5)更新分类器参数进入下一次迭代。

4　实验结果

本文的算法开发实现的硬件设备的配置为:i3CPU,2.4GHz主频,4GB内存,并在Windows7操作系统下在Matlab2012开发平台上实现。在三个有挑战性的图像序列上进行试验。图像序列在文献[12]中获取。

每段视频运行5次用2个指标来衡量跟踪性能:第1个指标为成功率(sr)。成功率定义为成功跟踪帧数nsucc与测试视频总帧数ntotal比值,具体定义如式(7)。成功跟踪定义为跟踪框与真实目标框交集与并集比大于0.5。

(7)

第2个指标为中心偏差(Center Location Error,CLE),定义为跟踪框中心坐标与真实框中心坐标像素偏差,见式(7)。

(8)

其中ROIx为跟踪框中心x坐标;ROIy为跟踪框中心y坐标。

本文和三个具有代表性的算法进行效果比较,主要和Compressive Tracking(CT)算法、The onlineAda Boost method(OAB)[13]、WMIL跟踪算法[9]行比较,本文使用这些算法作者提供的源代码,并将参数按照原作者提出的建议进行调整使得跟踪器获得最佳效果。

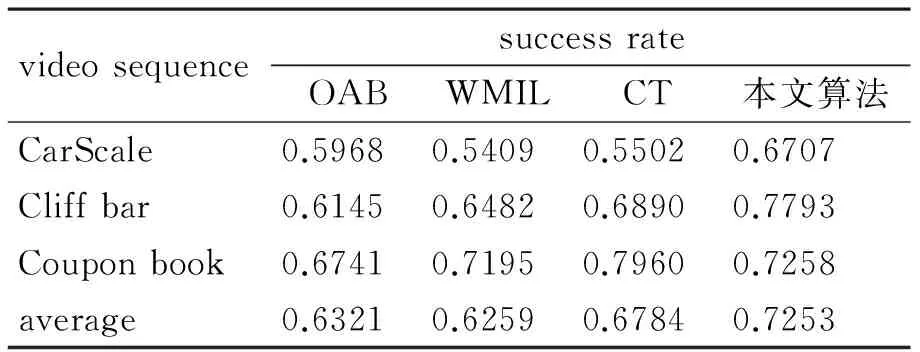
表1　成功率

表2　中心偏差

从表1和表2可以看到本文比CT算法在成功率上有提高,而中心偏差则降低。CarScale和Cliff bar跟踪目标由于存在明显尺度变化,在跟踪精确性上提升比较明显。Coupon book在尺度上变化不大,两者精确度差不多。因此在尺度变化较大的场景,本文算法更有优势。

图2　CarScale序列部分跟踪结果

图3　Cliff bar序列部分跟踪结果

图4　Coupon book序列部分跟踪结果

图2和图3和图4是测试视频部分跟踪结果,黑色框对应本文算法,灰色框代表CT,白色框代表OAB算法,粉色框代表WMIL算法。

图2 CarScale序列中目标尺度从小到大变化,从2帧开始目标尺度发生明显变化,跟踪效果图显示只有本文的算法跟踪框随着目标尺度的变化而变化,其余三个算法跟踪框并一直大小不变的,甚至偏移了目标中心,发生了漂移。图3 Cliff bar序列中目标尺度随着运动时大时小,尺度变化不均匀,跟踪效果显示只有本文的算法能跟随目标大小而变化,而其他算法的跟踪框一直是不变的,很显然不能及时随目标变化做出调整。图4 Coupon book尺寸虽然变化不大但是其形状发生了变化,但是本文算法和其他算法一样依旧对目标进行了有效的跟踪。

5　结语

本文针对传统的压缩跟踪算法存在的缺陷提出改进办法,提出一种新的基于自适应窗口的压缩跟踪算法,通过对比前后两帧图像跟踪框内的目标灰度均值变化,根据其比值建立了一种自适应窗口尺度调整的数学模型,实验结果证明该模型在跟踪过程中能自适应地随目标变化而及时调整跟踪框大小,而且改进后的算法在性能上也优于其他传统算法。

[1] Donoho D L. Compressed sensing[J]. Information Theory, IEEE Transactions on,2006,52(4):1289-1306.

[2] 卢雁,吴盛教,赵文强.压缩感知理论综述[J].计算机与数字工程,2012,40(8):12-14.

LU Yan, WU Shengjiao, ZHAO Wenqiang. Survey on the Theory of Compressed Sensing[J]. Computer and Digital Engineering,2012,40(8):12-14.

[3] 任越美,张艳宁,李映.压缩感知及其图像处理应用研究进展与展望[J].自动化学报,2014,40(8):1563-1575.

REN Yuemei, ZHANG Yanning, LI Ying. Advances and Perspective on Compressed Sensing and Application on Image Processing[J]. Acta Automatica Sinica,2014,40(8):1563-1575.

[4] Li H, Shen C, Shi Q. Real-time visual tracking using compressive sensing[C]//Computer Vision and Pattern Recognition(CVPR), 2011 IEEE Conference on. IEEE,2011:1305-1312.

[5] Zhang K, Zhang L, Yang M H. Real-time compressive tracking[C]//Computer Vision-ECCV 2012. Springer Berlin Heidelberg,2012:864-877.

[6] Candes E J, Tao T. Near-optimal signal recovery from random projections and universal encoding strategies. submitted to IEEE Trans[J]. Inform. Theory,2005,51(12):4203-4215.

[7] Achlioptas D. Database-friendly random projections: Johnson-Lindenstrauss with binary coins[J]. Journal of Computer and System Sciences,2003,66(4):671-687.

[8] Baraniuk R, Davenport M, DeVore R, et al. A simple proof of the restricted isometry property for random matrices[J]. Constructive Approximation,2008,28(3):253-263.

[9] Babenko B, Yang M H, Belongie S. Visual tracking with online multiple instance learning[C]//Computer Vision and Pattern Recognition, 2009. CVPR 2009. IEEE Conference on. IEEE,2009:983-990.

[10] 朱英宏,李俊山,赵怀勋,等.图像直线的描述与匹配算法[J].微电子学与计算机,2013,8:9.

ZHU Yinghong, LI Junshan, ZHAO Huaixun, et al. Description and Matching Algorithm for Line Matching[J]. Microelectronics & Computer,2013,8:9.

[11] Jordan A. On discriminative vs. generative classifiers: A comparison of logistic regression and naive bayes[J]. Advances in Neural Information Processing Systems,2002,14:841.

[12] Wu Y, Lim J, Yang M H. Online object tracking: A benchmark[C]//Computer vision and pattern recognition(CVPR), 2013 IEEE Conference on. IEEE,2013:2411-2418.

[13] Grabner H, Grabner M, Bischof H. Real-Time Tracking via On-line Boosting[C]//BMVC,2006,1(5):6.

A New Compressive Tracking Algorithm Based on Adaptive Window

WANG Long

(Nanchang Hangkong University, Nanchang330063)

This paper presents a new method of adaptive window method. Firstly the gray value in the tracking box of each frame is extracted, the mean value is calculated. Then the gray average between two frames is compared, a mathematical model is built for adjusting object size with an adaptive window by the ratio. Finally combined with compressive tracking algorithm, the changing scale object is tracked. It copes with the tracking window which do not change with the changing object during Compressive tracking algorithm. When the object size changes, the scale of the tracking window is adjusted. So tracking accuracy is improved. The experimental results show that the improved algorithm has better robustness than the original algorithm and the tracking performance has been improved.

compressive tracking, gray average, adaptive window

2016年3月11日,

2016年4月21日

汪龙,男,硕士研究生,研究方向:图像处理。

TP301.6DOI:10.3969/j.issn.1672-9722.2016.09.016