数列问题在全国卷与福建卷中的考查比较

王圣荣

（三明市第九中学，福建 三明 365001）

数列问题在全国卷与福建卷中的考查比较

王圣荣

（三明市第九中学，福建 三明 365001）

文章以全国卷和福建卷作为研究对象，对比历年文理科中在数列板块中的考查对象，先从题型上找到区别点，以便于抓住数列在全国卷中考查的比重和难度。然后再根据每个题目所涉及到的知识点，梳理出高三复习过程中应该重点讲解的知识点。解决了重点知识分布之后，接着再针对每个常见的重点知识，结合全国卷中典型的例题进行深入分析。在例题分析中总结各个题型的解题规律和教学建议，力求提升高三教学的有效性。

数列；高考；全国卷；比较

自2016年开始，福建省高考恢复使用全国卷，原来以创新和知识点交汇考查作为命题风格的福建卷在全国卷中能否延续，这直接决定高三的复习思路是否需要转变。有鉴于此，有必要对福建卷与全国卷的命题方式的异同点进行比较。

全国卷从2010年开始采用12道选择题，4道填空题，5道必做选择题及3选1的选作题的试卷模式，这一模式一直延续至今。另外在2013年之前，针对新课标地区的全国卷只有一份。到了2013年，随着实行新课标的地区增多，采用全国卷的地区越来越多，针对各地区的教育发展水平的不同，全国卷分为了全国Ⅰ卷和全国Ⅱ卷。这一模式一直延续至今。现以数列板块的内容作为分析对象，以2010年到2015年的全国卷数学试卷作为样本，对6年来全国卷与福建卷在数列问题的考查方式进行比较，力求在分析中为2016届的高考复习抛砖引玉。

一、历年高考试卷中的数列题型分布对比

通过对6年来所有样本试卷中的数列问题比较后，整理出如下的表格：（注：“选”表示选择题，“填”表示填空题，“解”表示解答题，后面的数字为所在题型的题号）

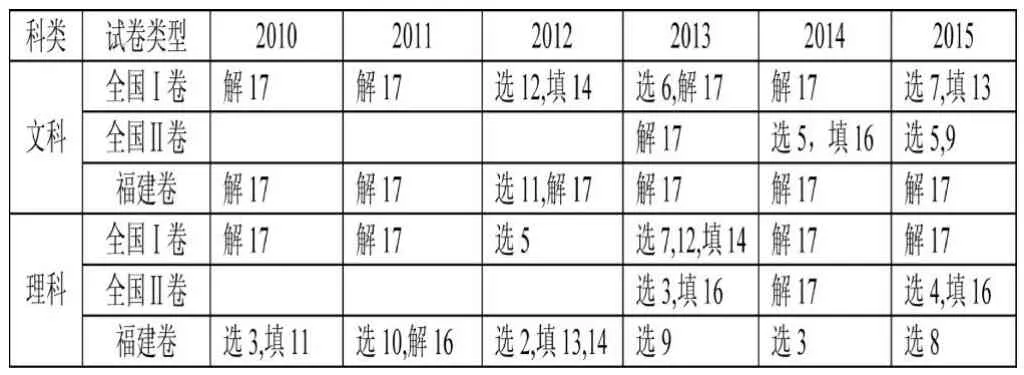
由此可以看出，无论文科还是理科，只从题目所分布的位置来看，三类试卷都放在相对靠前的位置，也就是说大都以基础题为主。以全国卷为例，18份试卷中有10份将数列放在解答题的第一题，占到近三分之二，其中文理科各占5份。

从全国两卷分析，三年的分卷时间，全国Ⅰ卷在文理科上都有两次将数列问题放在解答题，而全国Ⅱ卷却都只有一次出现在解答题部分。对比福建卷和全国卷依然可以看出，福建的文科卷将数列作为解答题的必考题型，理科卷则将数列作为小题的必考题型；全国卷文理科对数列的比较一致，数列是作为解答题的待选题型，尤其在全国Ⅰ卷中，大多数时候解答题的第一题都是以数列的形式出现的。而在选择填空题的安排上，与福建卷相似，全国Ⅰ卷更多的是将数列问题放在简单题的位置。全国Ⅱ卷则更偏向于只安排一道简单题，另一道数列的问题都是放在压轴题的位置。

再从分值上看，数列问题在全国卷中的分值为：文科约占10到17分，理科约占10到15分。

二、知识点的考查归纳与建议

如果以知识点的考查作为分析对象，那么通过整理样本卷得到如下的表格：

上表对样本卷中有关数列部分所考查的主要知识点进行罗列。通过表格可以看出：全国两卷都对基本量问题、求和问题和Sn与an的关系问题，而且全国Ⅰ卷对相关知识点的考查难度更大；全国Ⅱ卷则更重视这些知识点的基本应用，同时还增加对其他常见知识点的应用，如下表公式，递推公式求通项等问题的考查。可见全国Ⅰ卷更重视知识考查的深度，全国Ⅱ卷则更重视知识考查的广度。现针对这些特点，抽取其中一部分知识点进行必要的说明，不求面面俱到，但求能在教学中能够提供参考。

（一）递推公式求项问题

1.问题举例

递推公式求通项公式问题的方法有许多，如果每一种方法都进行深入学习的话，将要占用学生大量的时间，而且学习效果未必很好。庆幸的是在这类问题的考查中，大都只是放在小题中出现，这就为学生在使用常规方法之外提供了利用不完全归纳法进行猜想的机会。

如2015年全国2卷理科第16题：设Sn是数列｛an｝的前n项和，且a1=-1，an+1=SnSn+1，则Sn=___；

本题的常规方法是利用an+1=Sn+1-Sn的特点，在等式的两边同时除以SnSn+1，接着构造出等差数列后，得到Sn的通项公式。此外还可以用列举的方法，通过对n取1，2，3…求出相应情况下的，学生就能够很容易的归纳出Sn的通项公式应该是。

2.教学建议

通过列举后归纳出数列的通项公式是学生比较喜欢也比较容易接受的求通项公式的方法。教师可以在利用常规方法求通项公式的同时，尝试利用列举的方法求通项公式，这不仅有利于学生在小题的解答中提高效率，而且也能够在解答题中提高得分率。比如2014年全国Ⅰ卷理科第17题中，通过列举得到λ的值，最后再利用所得的通项公式证明满足已知的递推公式，同样可以得到正确的解答。

（二）基本量问题

1.问题举例

基本量问题首先要求学生熟练掌握等差、等比的通项公式、前n项和公式和中项公式，通过利用这些公式列出相关基本量的方程（如：首项、公差、公比等）。

如2013年全国Ⅱ卷理科第3题：等比数列｛an｝的前n项和为Sn，已知S3=a2+10a1，a5=9，则a1=（）

本题先根据数列｛an｝为等比数列，确定基本量为首项和公比，然后建立方程，解得。

在列方程问题中，一定要特别注意等比数列的前n项和Sn作为已知条件的问题。由于等比数列的前n项和公式存在q=1和q≠1的分类，所以在涉及到前n项和问题时，通常先采用前n项和的定义Sn=a1+a2+…+an，然后利用等比数列通项公式an=a1qn-1进行列方程，这样就能在列方程中避免分类讨论，使问题得到简化。当然在等差数列中就不存在这样的问题，可以直接利用公式列方程，即可得到所需的结果。

2.教学建议

针对基本量问题的复习，建议从简单的基本问题出发，让学生能够熟练地应用假设首项、公差、公比对已知条件列方程，这样的问题在教材的练习和习题中有许多，学生可以通过对教材中问题的解答，达到熟练应用公式和解方程的目的。完成了公式的基本训练之后，教师再拓展到其他技巧和方法的应用。最后采用复习资料中的例题和练习，循序渐进地提高学生综合应用的能力。

（三）求和问题

高中阶段的求和问题，常见的方法有四种：公式法、分组求和法、裂项相消法和错位相减法。鉴于公式法较为简单，分组求和法问题又较少出现，下面以裂项相消法和错位相减法为主，分别举例说明，并归纳其中的一般规律。

1.裂项相消法

裂项相消法在福建的样本卷中没有专门的考查，在全国卷中也只是在全国Ⅰ卷中出现三次考查到这一知识点，其中文科1次，理科2次，而且都是以解答题的形式出现，可见全国Ⅰ卷对这一知识点的重视。

裂项相消法所适用的数列通项公式通常需要满足三个特征：（1）分式形式；（2）分子为常数；（3）分母为同系数因式相乘的形式。学生在解题前需要先把所要求和的数列通项公式化简为满足以上三个特征的形式后，才能比较顺利地利用该方法解题。

如2015年全国Ⅰ卷理科第17题：Sn为数列｛an｝的前n项和，已知an＞0，an2+2an=4Sn+3。

（1）求｛an｝的通项公式；（2）设，求数列，最终得到所要的结｛bn｝的前n项和。

在第（1）小题得到an=2n+1后，观察到满足以上所列的三个特征，可以确定本小题应采用裂项相消法。接着同样先对各项进行列举，将｛bn｝的前n项和Tn整理为，然后利用分式的“化乘为减”的公式，得到果。建议对基础比较薄弱的学生利用分组求和的方式将整理为，通过两种形式的呈现，让学生能更容易理解最终结果的形成过程。

2.错位相减法

错位相减法是四类常见求和问题中最难的。在福建省的样本卷中从未考查到错位相减类的问题，与裂项相消法相同，错位相减法也只是在全国Ⅰ卷中考查过两次，文理卷中各有一次。错位相减法所适用的数列通项公式特征为一次指数或者一次×指数的形式。

如2014年全国Ⅰ卷文科第17题：已知｛an｝是递增的等差数列，a2，a4是方程x2-5x+6=0的根，

（1）求｛an｝的通项公式；（2）求数列的前n项和。

3.教学建议

在复习求和问题时，建议说明各种不同方法在步骤上的相同点：在数列规律不明确的情况下求和，首先都需要对求和的数列进行列举，列举中涉及到乘法、除法和指数的形式不进行计算或化简，保持原有的形式；然后通过观察所得结果，确定所使用的方法后，根据模式化的步骤对问题进行求解。特别是在裂项相消法的“化乘为减”和错位相减法的“同次相减”步骤的教学中，应尽量让学生自己动笔完成，以达到更好的教学效果。

（四）Sn与an关系的问题

1.问题举例

以2015年全国Ⅰ卷理科的第17题为例（题目见“裂项相消法”部分）。这类问题的解题步骤与数学归纳法的步骤相同。先取n=1，求得an=3；然后取n≥2，得到，结合公式可得an-an-1=2。由此可以判断出｛an｝是以2为公差的等差数列，结合a1=3求得｛an｝的通项公式。

2.教学建议

由于这一公式具有分类讨论的特点，在教学的过程中建议先从前n项和的定义出发，用形象的数字和形式发现前n项和都是从第1项开始一直加到最后一项。可以通过将n先用几个整数举例后，让学生更好的了解了公式的基本含义。接着通过例题演示和学生训练相结合，让学生熟练这一公式在实际应用中的基本步骤和书写方法。在学生熟练掌握公式的应用方法之后，教师可以给出与前n项和相关的递推公式求通项公式的问题，提高学生应用该公式进行解题的灵活度。从最基础的应用开始，循序渐进地提高题目的难度，既能抓好后进生的提高，又能让中等生夯实基础知识，还能让尖子生学有所获，达到提高课堂效率的目的。

从以上分析看出，福建卷对数列的考查，常与其他的知识板块结合，更加注重的是知识点之间的交叉应用能力。而全国卷与福建卷都对等差数列和等比数列在基本量问题的考查常抓不懈。同时全国卷的文科卷更注重考查学生对数列基本知识点的应用能力，掌握了知识点的应用方法，按照既定的步骤通常能够顺利得到完成问题的解答；而在全国卷的理科卷，尤其是全国Ⅰ卷中则越来越注重数列内在关系的探究，这从近两年理科卷中都考查利用Sn与an的关系对数列的探究就可见一斑。而在文科卷中对该知识点则毫无涉及。这也提醒教师在文理科的复习中对知识点的处理应该区别对待。

［1］林晴岚，陈柳娟，张洁.平中出奇常中创新—2013-2015年高考数学全国（课标）卷特色探析［J］.福建教育学院学报，2015（09）.

［2］李伟.全国卷形势下数学备考的策略［J］.课程教学研究，2015（12）.

［3］张先龙，邓军民.高考全国卷背景下的数学复习策略刍议［J］.课程教学研究，2016（03）.

G471.2

A

1673-9884（2016）05-0051-04

2016-04-28

王圣荣（1982-），男，福建福清人，三明市第九中学一级教师。