双边匹配理论下我国研究生调剂体系的最优性研究

秦放鸣，焦音学

双边匹配理论下我国研究生调剂体系的最优性研究

秦放鸣，焦音学

双边匹配理论自20世纪60年代初次提出至今，应用遍及金融、教育等多个领域。国外通过双边匹配理论与大学招生模型相结合，实现了高等教育不同模块的最优机制，而我国双边匹配理论虽在高考领域已见成效，但硕士研究生招生考试则涉及较少，特别是较为复杂的调剂体系。因此，依据双边匹配理论现有成果，以大学招生模型为基础，可从个人理性、帕累托最优等5个方面对我国研究生调剂体系的最优性进行考察。结果显示，研究生调剂体系理论上未达最优，现实情况更为严峻，未来仍需深入完善。

双边匹配理论；递延接受算法；研究生调剂体系；最优性

一、引言

近些年，我国硕士研究生招生考试（以下简称“考研”）报考人数已达160余万且连年走高，竞争激烈，每年考试过后皆是“几家欢喜几家愁”，对于初试成绩未达到目标院校分数线的考生而言，尽管还有其他可供选择的继续深造方式，但除直接就业以外，大多数考生还是将通过研究生调剂系统进行调剂作为主要选择，即另外争取尚有缺额的招生单位复试以实现考取硕士研究生这一目标。作为考研的一个重要组成部分，研究生调剂与高考招生体系等过程一样，是一个学校录取机制问题，也是考生和招生单位之间的匹配问题。双边匹配理论是当前对市场中两个不重叠的参与人之间如何依据偏好进行合理组合的一项重要研究，学校录取机制问题在现实中正是该理论在教育领域的应用对象之一，其主要目的是在学校招生名额有限的情况下，如何设计制度使学校和学生之间的匹配可以更加合理，并使效率最大化，在我国该问题长期为多方热议，高考招生、研究生招生制度前后多次改革，都力求寻觅到更优匹配方式。研究生调剂系统经过多年发展，如今已趋于成熟，形成以中国研究生招生信息网（以下简称“研招网”）为主要载体的线上线下同步系统，然而大部分考生虽可借此获得二次录取机会，但每年遭遇“调剂滑铁卢”而于次年重新报考者却也为数不少。目前，已有研究成果主要针对硕士研究生考试整体进行展开，力图寻求整个机制的完整有效，但针对其中较为特殊的调剂体系研究尚不多，由于研究生调剂体系在整个机制中相对独立，更类似于初试过程的二次延伸，因此本文拟以双边匹配理论为视角，对我国研究生调剂体系运行状况进行考察研究。

二、文献综述

双边匹配理论以信息经济学、博弈论等相关学科为基础，最早产生于婚姻匹配问题。Gale和Shapely（1962）首先针对男女伴侣间结合不稳定的问题，提出一种解决男方、女方间择偶选择的婚姻匹配策略，并证明该过程存在非空稳定匹配，在此基础上，他们设计出双边匹配理论的基本算法——递延接受算法，即“Gale-Shapely机制”，同时通过大学招生模型，证明递延接受算法可以让申请者严格偏好假设下都获得稳定匹配［1］。这两部分内容标志着双边匹配理论正式成型。随后Shapely和Shubik（1972）对“Gale-Shapely”机制进一步扩充，将货币因素考虑引入算法中并作为效用衡量标准之一，重新定义了包含价值支付的双边匹配市场，提出一种包含货币因素的新型匹配理论模型——“派遣博弈模型”，重点对匹配中的“核”进行考察［2］，以该理论为基础，双边匹配理论逐渐在各个领域内得到实践应用。

Roth（1984）再次依据美国医学院实习生劳动力市场发展历程，对其内部长期运行的机制——NIMP算法进行考察，发现其实际与递延接受算法一致，保证了市场运行的最优［3］。1998年，Roth和Peranson再一次针对美国医学院毕业生的失业问题，利用双边匹配理论加以改进，并成功将改进后的机制列入当年“全国住院实习生分配计划”（NRMP）中［4］。此后，双边匹配理论逐步形成理论与实践齐头并进的发展态势趋于稳定，直到2012年，Jean、Filomena等人再一次对“Gale-Shapely”机制深入考察，以离婚问题作为案例，得出“Gale-Shapely”机制决定的婚姻匹配内部稳定性会因外部新进入者而遭到破坏，因此还需要引入“外部稳定性”这一概念，整个机制要稳定匹配还必须保证外部稳定性［5］。

双边匹配理论进入我国后，由于在理论方面已成体系，故而很快于理论和实践中同时展开，其中金融业是最早获得应用的领域之一。文胜（2006）在对双边匹配理论结构框架完整概括后，通过分析中国银行信贷市场所面临问题而推算出市场间存在的博弈和匹配过程，并指出就此可对不同业务内容进行了匹配机制设定［6］。沈丽、石彦（2013）通过梳理双边匹配理论发展历程，总结双边匹配理论在国内各领域的应用及其相关研究基础上，重点分析其在金融市场应用状况［7］。以金融业为开端，双边匹配理论其后逐渐在电子商务、大学生就业、会计审计等各大领域展开。张振华、贾淑娟（2008）研究了双边匹配理论的稳定性条件，将“Gale-Shapely”和“HR”算法在理论上由一对一形式扩展至多对多匹配——“p-k”形式，最终以此算法对电子中介中买方与卖方之间进行满意度设定，推算多对多匹配之间稳定性过程［8］。王塑、李西平（2013）同样指出人员—岗位之间是一种双边匹配决策过程，可依此设立更为完善的人员—岗位相互之间双向评价指标体系，最终结果则通过模型化加以证明［9］。张成（2010）依据我国大学生劳动力市场发展现状的分析，在就业过程、信息获取、招聘方式及流程等方面得出当前我国大学生就业市场存在的问题，进而以双边匹配理论为基础，建立我国大学生劳动力市场的稳定匹配模型，亦对模型在不同市场机制下实际应用的可行性进行了探讨［10］。刘鑫（2014）针对大学生职业规划问题，认为学生与用人单位之间也存在双边匹配关系，因此可将企业评价学生的“敏感性偏好”依据双边匹配理论指标化，以建立学生职业规划评级模型［11］。王杏芬（2015）以国内会计审计市场发展为研究内容，发现国内现有大小事务所与接受服务群体之间弊端较多，以双边匹配理论为支撑，对会计事务所低价竞争与品牌竞争间的关系进行实证检验，最终结果显示目前国内审计市场恶性竞争较为严重［12］。

金融行业在国内虽然应用最早，却非应用最广，教育行业在双边匹配理论进入后逐渐成为应用最集中的领域，并以高考志愿录取机制为重点方向。聂海峰（2007）先以数学模型对高考知分录取模式下考生志愿报考博弈过程加以分析，指出目前仍存在的“高分低就”现象，说明当前志愿填报机制尚未达到最优，进而在“Gale-Shapely”机制基础上提出了改进模型，提出分数独裁机制将可以更加保障匹配结果稳定性［13］。以该研究为基础，魏立佳（2008）开始对双边匹配理论下学校录取问题模型加以总结，通过比较“Gale-Shapely”机制、最优交易循环机制等四种匹配机制概念、特点，在对现存高考志愿填报机制存在的问题及改进措施分析后，进一步设计了与高考录取机制相异的博士录取机制，并证明现行博士招生机制因为非帕累托最优而非最优机制［14］。李坤明（2010）则重点分析波士顿机制下匹配的稳定性与效率，以资源匹配视角、完全信息视角和非完全信息视角三个方向为视角，考察现行高考录取机制的效率特征，最终在验明我国高考招生系统所存在问题并分析试行高考新机制：“平行志愿”模式后，提出改进设想和新算法模拟步骤［15］。

可以看出，双边匹配理论源于实践，同时又反应用于实践，在理论成型后迅速应用到包括教育、金融、人力资源等各大领域。在我国，高考作为全国“最大考”，成为双边匹配理论的应用重点。相比之下，研究生招生及其复杂的调剂过程在这方面关注甚少，因而借助双边匹配理论考察这一内容，无论对研究生招生调剂本身，还是对其他教育领域，都具有重要指导意义。

三、研究生调剂体系与高考录取机制、博士录取机制的对比分析

高等教育入学考试（以下简称“高考”）、硕士研究生招生考试（以下简称“考研”）和博士研究生招生考试（以下简称“考博”）由低到高、层层递进，不仅是我国高等教育的三大入门考试，也是整个体系的三条支撑点。高考由于参与人员众多，长期被形容为“千军万马过独木桥”，年年皆属社会关注焦点，而考研与考博的关注则相对较少。从整体来看，我国高考招生体系的特点是整个过程完全由国家主导，考生参加由国家统一举行的考试，然后估分填报志愿，若满足提前批次或第一志愿所报院校分数线（上档），则其考试档案由拟录取学校调阅审核后完成录取；如果考生不幸分数未达要求（掉档），则继续根据其所报平行志愿进入由国家统一组织的调剂流程，若其平行志愿院校尚有招生名额，则完成录取，反之则落榜，整个高考过程中始终由国家招生机构来组织学生和院校之间的匹配。根据双边匹配理论，高考是一个中心化市场，属于单次统一录取机制（图1）。博士招生体系则正好相反，其特点是考试流程完全由各招生单位自行主持，考生先自行搜集各招生单位博士招生信息并参加初试，若初试成绩满足招生单位要求，则进入复试环节，通过即博士录取，反之则落榜。由于各招生单位考试时间并不一致，故若考生参加某招生单位初试或复试未通过，仍可以参加其他招生单位考试，理论上考生可以同时报考多家招生单位，被录取后亦可筛选拟录取招生单位，确定最终选择。因此，博士招生考试是一个非中心化市场，复试是考博流程中的一个节点，属于单次非统一录取机制（图2）。

相对而言，“考研”过程较为特殊：第一，整个流程中调剂过程与上线过程相对独立。作为考生，对于其所报志愿招生单位的复试分数线，无论过线还是未过线，都必须等待至调剂结束后的复试阶段，因而以“国家线”出台为分水岭，志愿过线考生与志愿未过线考生分别进入等待复试和调剂两大环节，直至复试环节汇合，这实际已成为两个相对独立的过程。第二，研究生调剂体系兼具统一录取机制和非统一录取机制两重特点。复试仍是整个流程体系中的一个节点，不论考生直接过线还是未过线调剂，最后都要集中进入复试环节由各招生单位进行复试至录取。在复试之前，考生统一通过“研招网”报名参加全国硕士研究生招生考试（初试），并由国家发布统一分类的“国家分数线”（简称“国家线”，34所自主划线高校除外），过“国家线”及招生单位分数线的考生直接进入复试环节，而仅过“国家线”却未过招生单位分数线的考生，则统一在“研招网”调剂系统参与研究生调剂，并等候申请调剂招生单位的回复，这一过程与高考招生过程异曲同工，当调剂结束，各招生单位则各自组织对申请的考生进行复试，进而完成录取，这与博士招生过程又有所相似（图3）。

因此，硕士研究生招生考试以“国家线”公布为起点划分为两个相对独立的过程，其中之一即是调剂体系。研究生调剂体系以复试环节为节点，前、后两段分别与高考录取机制、博士招生机制有所相似，故对双边匹配理论下硕士研究生招生体系的研究亦可以划分为两部分，即“调剂-复试”阶段和“复试-录取”阶段。

四、双边匹配理论下学校招生模型概述

图1　高考录取流程

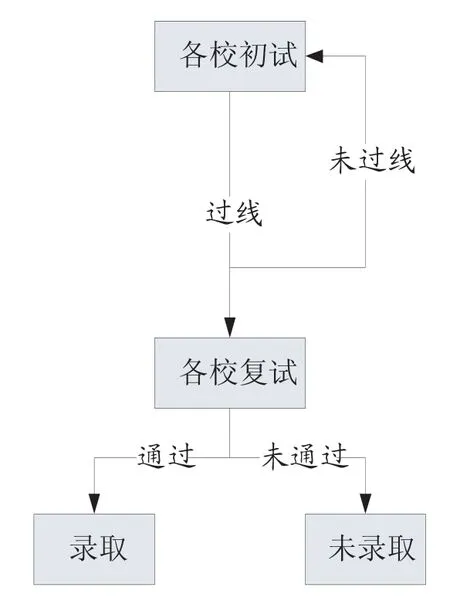
图2　考博录取流程

图3　考研录取流程

Gale和Shapely根据婚配问题提出“Gale-Shapely机制”后，继续将其延伸至学校招生领域，设计出“G-S机制”下的大学招生模型，随后以该机制为基础，在这一领域内衍生出最优交易循环机制、波士顿机制和分数独裁机制其它三种匹配算法。在双边匹配理论框架下，大学招生问题可视为寻求满足公平性、无浪费性、帕累托最优等条件的最优机制，其基本模型可表述为以下形式：

定义1：每个学校录取人数不多于录取名额，即存在个人匹配过程：Ui=μ（Sj），对于任意Ui，

定义2：在整个机制下，每个学生对学校偏好的排序与学校匹配结果一一对应，即Psj→μ（Sj），P→∑μ（Sj）。

定义3：匹配过程μ是公平的。任意两个学生S1和S2，如果相对于录取自己的学校，S1的偏好要低于录取S2的学校，那么录取S2的学校对S2的评价一定高于S1，即∀S1、S2，Ui=μ（S1），μ（S1）Ps1μ（S2），则Tu（S1）＜Tu（S2）。

在上述设定之上，最优大学招生模型满足以下条件：

条件1：匹配过程μ不存在浪费。若有任意学生Sk、学校Ui，学生较其他学校更偏好Ui却未被Ui录取，则学校Ui一定已经录取招生名额lui人，即如果UiPskμ（Sk），则

条件2：每个学生在匹配过程μ中是理性的。对单个学生而言，所有学校匹配结果一定不会比没有学校可去更差，即对于任意学生Sk，μ（Sk）PskU0或者μ（Sk）=U0。

条件3：匹配过程μ具有稳定性。对任意学生S1、S2，若相比其他学校S1更偏好学校Ui，而学校Ui选择录取S2，则二者间Ui对S2一定给予更高评价，即如果μ（S2）Ps1μ（S1），Ui=μ（S2），则Tui（S2）＞Tui（S1）。

条件4：整个机制运行具有抗策略性。对于每位学生而言，其依靠真实偏好匹配学校的结果一定会好于或等于采取策略调整偏好的结果，即假设整个机制为M，对于任意Sk、Psk，有M（Psk）≻M（P′sk，Psi）或M（Psk）=M（P′sk，Psi），其中M（P′sk，Psi）表示其他人依据真实偏好填报而学生Sk采取策略调整偏好时的机制，也就是说学生在机制下不存在隐藏真实意愿的动机，按其真实想法申报匹配的学校最为理想。

条件5：匹配过程μ帕累托最优，不存在其他匹配过程可以进行帕累托改进，即对于任意学生Sk，不存在另一种匹配过程μ′，使μ′（Sk）Pskμ（Sk）或μ′（Sk）=μ（Sk）。

在最优的大学招生机制下，学生与学校身份不时在发出者和接受者之间转换，实际形成一种动态循环，在结束前双方都没有完全将对方确定，始终在变换寻求最优选择，当所有学校的邀请都被接受或没有学生的申请被拒绝时，循环停止，最终各学生与各学校间取得最合适的匹配组合。

五、我国研究生调剂体系的最优性研判及结论

高考与考博的主要区别实际在于匹配过程中间是否存在中介参与协调双方间匹配，即统一与非统一问题。研究生调剂体系与高考、考博一样，都属于单次录取机制，但在“调剂-复试”阶段，所有考生必须通过“研招网”向招生单位申请调剂，所有招生单位也必须通过“研招网”发送信息和反馈考生，因而可以认为“研招网”发挥了高考招生办公室的职能；进入“复试-录取”阶段，则由各招生单位自主对参与复试的考生进行筛选，实际过程与博士复试无二，因此对研究生调剂体系整体的考察需要先对这两个过程予以划分，并且分别设定。根据以上研究生调剂体系之特点，以大学招生模型为基础，进一步设定研究生调剂模型：

（1）由于调剂已是权衡后作出的选择，因而当某个考生选择调剂时，它一定优于其它选择，即考生Sk的偏好排序Psk中，不包含不上学U0｛｝。为方便分析，这里假设所有招生单位复试分数线皆以“国家线”为标准，暂不计自主划线情况。

（2）由于各招生单位公布复试信息、组织复试时间既有相同也有不同，故设定招生单位在“调剂-复试”阶段的时间集｝，其中表示招生单位ui第d个通知考生复试，k＜d≤z）表示uj早于ui通知考生复试；“复试-录取”阶段时间集｝，其中表示招生单位ui第h个完成录取，h≤t）表示uj早于ui完成录取，且

（3）“申请-复试”阶段招生单位Ui以考生初试成绩构成评价集Tui，设考生Si的初试成绩为ci，该阶段｝；“复试-录取”阶段招生单位Ui以考生复试成绩构成评价集Tui，设考生Si的复试成绩为bi，该阶段

（4）由于各招生单位调剂名额只是最终录取名额的一部分，故设接受调剂的名额为F=｝，并按1.2fui的投档比接收调剂申请。

（5）“申请-复试”阶段有复试匹配过程：Ui=η“复试-录取”阶段有拟录取匹配过程：

（6）在“调剂-复试”阶段，“研招网”对考生同一时间提交调剂申请的名额限定为2个，因此这里假设考生在某时间段申请调剂时，根据已公布信息保留偏好前两位的招生单位，即对于∀Rui，P=学生Sk该阶段招生单位偏好中前两位的排序。

由此，我们可以对研究生调剂体系两个阶段的算法描述如下：

1.“申请-复试”阶段

准备阶段：Rs0时刻，考生S根据“研招网”上各招生单位的调剂信息情况，设定各自的偏好，并对其中的招生单位进行申请——

第z步后，所有招生单位U均完成了一轮调剂选择，算法结束。

2.“复试-录取”阶段

准备阶段：Os0时刻，考生S对相同录取时段内的招生单位选取最偏好者进行复试——

第t步后，所有招生单位U均完成一次录取，算法结束。

整个考研调剂体系运行过程至此结束，根据以上描述，通过对研究生调剂体系的考察，我们得出以下结论：

结论1：现行研究生调剂体系是个人理性的，也是公平的。

首先，由于设定考生参加考研调剂是选择后的结果，那么在初试结束至考研调剂前这段空档期内，考研调剂一定是经过比较后要优于包括直接工作在内的其他方式而成为考生选择，根据定义，现行研究生调剂体系是个人理性的；其次，考生是否能为招生单位录取最终取决于其复试成绩，即Tui＝对于若，则一定存在，考生S1的复试成绩一定低于考生S2。即使在“调剂-复试”阶段，由于招生单位是按考生初试总分由高到低录取，因此以上推导亦适用此阶段，故而研究生调剂体系也是公平的。

结论2：现阶段研究生调剂体系不是无浪费的，也不是帕累托最优的。

对于考生来说，在体系中的任何一个环节对招生单位进行拒绝都是无效用损失的，因此存在以下可能：在ouj时刻，有且，但到之后的ouk时刻，则有μ此时匹配结果出现luj-1，此时录取过程已结束，考生Sl并未为招生单位Uj拟录取，招生单位Uj也并未录满招生名额luj人，产生了录取名额的浪费，进一步，若这个浪费的名额给予考生Sl，则又是一种帕累托改进。同理，以上可能也存在于“调剂-复试”阶段，造成复试名额的浪费和相应的帕累托改进，因此现行研究生调剂体系存在名额浪费情况，非帕累托最优。

结论3：现行研究生调剂体系是非抗策略的。

对于调剂中的所有考生S而言，各自的偏好均是私人信息，所申报的招生单位仅知晓UiPsU0，但考生却可以依据自己的分数与“国家线”之间的差距来进行判断，存有策略选择的动机，故有如下可能：

假设某一时段内，有S1、S2、S33名考生，各自分数分别为370、360、335，“国家线”为330，有招生单位U1、U2、U33所，各自复试名额为1、1、2，S1、S2、S3各自的偏好为：S1—U1≻U2≻U3、S2—U1≻U3≻U2、S3—U2≻U1≻U3。若按真实偏好进行调剂申请，3名考生各自报送结果为：S1（U1，U2）、S2（U1，U3）、S3（U2，U1），最终复试名额匹配结果为：S1→U1+U2、S2→U3、S3→U0，若S3采取策略偏好S3（U2，U3），则最终复试匹配结果为：S1→U1+U2、S2→U3、S3→U3。

结果表明，S3通过隐藏其真实招生单位偏好，通过U1→U3这一策略性手段获得了更优的结果（U3≻U0），因而研究生调剂体系是非抗策略的。

总体来看，现行研究生调剂体系满足个人理性和公平性两大要求，但并不满足最关键的无浪费性、帕累托最优和抗策略性，这也至少说明了现实中一个最为明显的现象，即每年研究生“调剂-录取”结束后，都会有大量考生没有成功调剂，同时也有相当一部分招生单位无法录满名额。因此现行研究生调剂体系并不是一个最优机制，它在考生和招生单位两端都导致了额外效率损失和成本增加，使得很多考生无奈放弃，迫使很多招生单位展开“二次调剂招生”。

六、目前我国研究生调剂体系存在的主要问题

为方便研究，本次对研究生调剂体系的最优性研究基于现实进行了严格假设及条件简化，但实际情况表明，研究生调剂体系还要受多方外部因素干扰，这些问题主要表现在以下几个方面：

第一，调剂志愿时间锁定问题。考生通过“研招网”申请的调剂志愿并不是严格伴随招生单位调剂信息的公布时间，而是每项志愿锁定48小时后方能解锁更换，因此考生为保证自己被所偏好的招生单位最大可能录取，必然不会于同一时间将两个志愿全部使用，即两个志愿之间存在不等的时间差，加大了考生策略申报的可能。

第二，调剂信息迟滞问题。首先是招生单位在“研招网”公布的调剂信息通常只有调剂名额、调剂要求等部分信息，无法涵盖所需准备的材料等具体细节，这些往往需要考生进行电话询问；其次是部分招生单位负责调剂的工作人员在接听考生电话询问时解释不清、缺乏耐心，使得考生难以获取详尽的相关信息，双方信息不对称加剧。伴以上述调剂志愿时间锁定问题，直接导致许多考生与自己偏好靠前的招生单位擦肩而过。

第三，自主划线院校问题。国家现有34所自主划线高校，其中部分高校也拥有调剂名额，但这些高校不以“国家线”为标准，而以自划分数线为主，故对学生的评定也与以“国家线”为标准的大部分招生单位有所差异。另外，自主划线高校复试时间通常早于“国家线”下的招生单位，前者大约在3月底，后者则集中于4月初，中间存在着一段间隔，一定程度上增加了考生参加多次复试后再选择的可能，间接造成部分普通招生单位的名额浪费。

第四，考生“择校底线”问题。这一问题主要在于考生心中多有一个作为底线的招生单位，该单位通常为考生母校，即母校成为考生的预期标准，低于该标准过多的招生单位将会让考生难以接受，直接放弃调剂。此外，该问题多与前述问题相伴出现，即考生连续错过自己偏好的招生单位，当时间合适时，可选意向又大部分都低于预期，这类心态的考生大量退出导致许多欠发达地区的普通招生单位雪上加霜，甚至出现“二次调剂”后仍然招生未满的现象。

七、优化我国研究生调剂体系的相关对策建议

以上所述主要问题的实际表现为：每年临近研究生招生调剂，诸考生皆是草木皆兵，牵一发而动全身。外部因素的干扰与机制本身的不足共同造成现行研究生调剂体系的问题存在，整个体系的持续更新将是一个长期过程，在中、短期内，至少应在以下几个方面，对研究生招生调剂体系整体进行完善优化。

第一，树立“研招网”权威，强化约束作用。就目前而言，研究生调剂体系无法如高考体系一样形成完全的中心化市场，但以上四个方面存在的问题皆是人为因素所致，而缺乏足够的约束监督是一个重要原因。笔者认为，“研招网”未来需要进一步完善成为研究生调剂体系的中枢，在作为调剂参与平台的同时，还应在信息发布等方面对各招生单位进行规范化管理，对消极回应等问题形成监督，同时亦可设立申诉渠道，给予考生参与监督权。

第二，尝试在各招生单位间分批次划分，照顾弱势招生单位。目前对各招生单位的基本划分仅为“自主划线”和“国家线”两类，但在实际调剂过程中，以“国家线”为基准的东部“985”“211”高校等重点招生单位申报考生多且名额不足，而众多的普通招生单位，特别是西部地区的高校，几乎年年因调剂申报不足而名额浪费，“二次调剂”问题也基本发生于这类群体之中。因此，参考经济学中价格歧视理论，可尝试在现有基础上对“国家线”下招生单位按实力、地区等划分批次，再按批次划分不同的调剂时间段，减少考生因调剂时间问题带来的无谓损失。

第三，强化自律意识，提升服务形象。各招生单位应明确职责、履职尽责，加强职业自律，端正服务态度，尽量详细公布包括考生所需材料在内的调剂信息，保证信息透明化，让考生知晓复试难度、差额比例等，以便考生综合评估自身实力，减少盲目填写无效志愿造成损失。各招生单位通过调剂平台发现申报考生存在条件不符及调剂名额告罄时，应尽快解锁调剂志愿并告知考生，由于考生调剂分秒必争，不仅可以避免浪费考生时间，也体现出招生单位关爱考生、理解考生，不断提升服务质量，树立良好的服务形象。

第四，考生合理设计自身的调剂计划。首先，在调剂系统开始前，考生可通过往年资料与意向招生单位进行咨询、沟通，剔除无机会的目标，特别是一旦无缘目标院校，应立即告知对方解除志愿锁定；其次，考生的“名校情结”在调剂前需加以权衡，即要么来年再考，要么进入调剂，接受低于心理预期的可能结果；最后，考生要认真备战复试，一方面要巩固专业知识体系保证笔试，另一方面更要重视面试，调整心理，收获成功。复试是调剂的“收官”，若考生于复试被刷，不仅本次调剂告之失败，还往往因此时调剂阶段已近尾声而丧失所有调剂机会，费力而不讨好。

总体而言，我国研究生调剂体系作为硕士研究生招生最复杂的一部分，兼备博士招生和高考招生的两方特点，现行研究生调剂体系通过双边匹配理论被证明仍有待完善。依据双边匹配理论设计的各项机制已被国外广泛应用，在此背景下，理应对其中的成功案例加以借鉴，进而推动未来我国硕士研究生招生调剂体系愈加完好，直达优化。

［1］Gale D and Shapely L.S.College Admissions and the stability of marriage［J］.American Mathematical Monthly，1962，（69）.

［2］Shapely L.S.and Shubik M.The assignment game I:the core［J］.International Journal of Game Theory，1972，（1）.

［3］Roth A.E.The evolution of the labor market for medical interns and residents:a case study in game theory［J］.Journal of Political Economy，1984，（1）.

［4］Roth A.E.and Peranson E.The redesign of the matching market for American physicians:some engineering aspects of economic design，［J］.The American Economic Review，1999，（4）.

［5］Jean J.Gabszewicz，Filomena Garcia，Joana Pais，et al.On Gale and Shapely“College Admissions and the Stability of Marriage”［J］.Theoretical Economics Letters，2012，（2）.

［6］文胜.双边匹配理论在中国银行信贷市场中的运用［D］.华中科技大学，2006.

［7］沈丽，石彦.双边匹配理论及其在金融市场应用的研究综述［J］.金融发展研究，2013，（6）.

［8］张振华，贾淑娟.基于稳定匹配的电子中介匹配研究［J］.控制与决策，2008，（3）．

［9］王塑，李西平.基于双边匹配理论的人员-岗位适配性研究［J］.人力资源管理，2013，（12）.

［10］张成.双边匹配理论及其在我国大学生应届毕业生劳动力市场的应用［D］.华南理工大学，2010.

［11］刘鑫.基于双边匹配理论下的个性化职业指导与模型研究［J］.科技创新导报，2014，（23）.

［12］王杏芬.审计市场格局：低价竞争抑或品牌竞争——基于匹配理论的实证检验［J］.山西财经大学学报，2015，（6）．

［13］聂海峰.高考录取机制的博弈分析［J］.经济学（季刊），2007，（3）．

［14］魏立佳.中国高考录取与博士生录取的机制设计［J］.经济学（季刊），2009，（1）.

［15］李坤明.基于双边匹配理论的中国高考录取机制研究［D］.华南理工大学，2010.

［责任编辑：刘烜显］

秦放鸣，新疆大学经济与管理学院教授，博士生导师；焦音学，新疆大学经济与管理学院硕士研究生，新疆乌鲁木齐830046

G643

A

1004-4434（2016）08-0166-07

2015年新疆大学世川良一优秀研究生科研资助项目（XJU-SYLLF15003）研究成果