地面起伏特征与铁路工程规模关系探讨

赵金顺　彭建锁

(中铁工程设计咨询集团有限公司，北京　100055)



地面起伏特征与铁路工程规模关系探讨

赵金顺彭建锁

(中铁工程设计咨询集团有限公司，北京100055)

铁路沿线地形起伏对沿线的工程分布有着重要的关系，利用统计学的原理揭示地形起伏与铁路工程规模相应关系的研究非常必要。研究表明，以6～10 km范围内地面起伏高差的各项统计指标，经过主成分分析可以更有效地确定工程规模，以地面起伏高差或其各项统计指标构成的主成分作为连续变量，能够快速计算工程规模。

地面起伏铁路工程桥隧比

一条铁路线路连绵数十公里或者几百公里，经历不同的地貌单元，有着不同的起伏特征和不同的工程分布特征。大量的实践证明，铁路线纵断面起伏大，铁路工程相应艰巨，表现在桥梁、隧道或者路基工程大，从而铁路工程规模也大。因此，探讨铁路线路纵断面起伏特征与铁路工程规模间的相关关系，对铁路线路设计有着重要的意义。

1　铁路工程规模特征指标

铁路工程规模的影响因素很多，一般情况下包括以下四个方面。

(1)沿线自然地理因素

包括地形地貌、河流水文、工程地质、水文地质、气候条件等。

(2)沿线人文地理因素

包括矿产资源分布、城镇分布、工矿企业分布、各种人工建筑物分布等。

(3)铁路线路主要技术标准

包括铁路性质、正线数目、平面条件、纵断面条件以及运输现代化水平的特征等。

(4)设计水平及施工技术水平

集中反映铁路线路与自然地理因素、人文地理因素、铁路技术标准的巧妙结合。结合得好，沿线工程规模就小，对自然的破坏就小，从而就会有好的经济效果。

在这些因素中，地形地貌对铁路工程规模具有重要的影响，正如我们常常感知到的一样，平原地区的铁路造价比山区的铁路造价要小得多。

铁路线路工程包括路基工程(包括站场内路基工程)、桥梁涵洞工程、隧道工程、轨道工程、电气化工程，以及通信、信号、信息、房屋建筑、给排水等。一般说来，路基、桥涵、隧道、轨道、电气化工程构成铁路主体工程，约占工程造价的半数或更多。桥隧所占线路长度比重有时可以反映铁路工程的艰巨程度或造价。不同桥隧比重条件下工程造价比见表1。

表1　不同桥隧比下每公里铁路造价比

在缺少相应资料的前提下，采用桥隧比作为工程规模的反映。

2　地面起伏高差特征

线路纵断面填挖高度既是分界桥梁工程、隧道工程、路基工程的重要指标，也是自然地面起伏状况的反映。因此，采用地面高程与设计高程差(后称起伏高差)来描述地面起伏特征，以铁路里程为横轴，铁路沿里程起伏高差为竖轴，其地面起伏典型特征表现如图1、图2、图3所示。

图1　铁路线路纵断面地面起伏情况

图2　地面起伏高差分布

图3　地面起伏高差相关系数

(1)从图1可以看出，在不同的铁路里程处，地面起伏高差是不一样的，整体上来看，起伏高差有稳定的一面，也有随机的一面，在不同的里程范围，起伏高差不同且其分布的规律不同，有着随机过程特征。

(2)从图2可以看出，地面起伏高差分布并不对称，表现在挖多填少，这与工程设计有着密切的关系。

(3)从图3可以看出，任意两里程的地面起伏高程差之间具有相关性，表现在随两点之间的距离增加，相关性减低。大致表现为300 m之内高度相关，300～1 100 m中度相关，2 100 m以远基本无关。

运用随机变量特征分析的方法有助于提取纵断面特征。一般说来，对随机变量特征的提取包括四个方面：①随机变量概率密度特征；②随机变量均值、方差、方均值及方值方差等数值特征；③随机变量自相关特征；④随机变量谱密度特征。为了便于研究，本文先期提取随机变量数值指标作为研究。

2.1地面起伏高差数值指标

结合随机变量数值指标的物理意义选用以下指标。

(1)某一长度范围内绝对起伏高差之平均值Y1

既能反映纵断面起伏程度，也能反映铁路工程填方高度或者挖方高度，反映路基工程大小、平均桥梁高度、平均隧道埋深等。

(2)某一长度范围内绝对起伏高差之方差值Y2

可以反映填方高度或者挖方高度的绝对值偏差，反映路基工程大小、桥梁高度、隧道埋深偏差程度等。

(3)某一长度范围内起伏高差方值之平均值Y3

是随机变量重要的统计指标(侧面反映平均功率)，反映谱密度特征，是填方高度或者挖方高度平方值的平均值，反映铁路路基工程大小，侧面反映桥隧困难程度等。

(4)某一长度范围内起伏高差方值之方差值Y4

反映填方高度或者挖方高度平方值的偏差，反映路基工程大小、桥梁高度、隧道埋深偏差程度等。

(5)某一长度范围内起伏高差之极差值(100%，0%)Y5。

(6)某一长度范围内起伏高差百分位(75%，25%)差Y6。

2.2地面起伏高差数值指标特征分析

考虑地面起伏高差2 000 m以内的自相关性好，为避免统计上的复杂性，取某一长度为2 km，计算出该范围地面起伏高差数值指标。总体样本各项指标分布特征见图4。

根据统计学原理，对上述数值指标进行分析，可以得出以下结果。

(1)从图4可以看出，从整体样本分布来看，各项指标的分布并不均匀，各自的分布规律并不相同，反映出所选用的样本有所偏重，分析结果有可能仅适应于有限范围。

(2)对于多项数值指标，ln(Y1)取值在0～6之间，基本符合韦伯分布；ln(Y2)取值在-2～9之间，基本符合正态分布；ln(Y3)取值在0～12之间，基本符合韦伯分布；ln(Y3)取值在2～20之间，基本符合正态分布；ln(Y5)取值在1～5之间，ln(Y6)取值在-2～6之间，基本符合正态分布。

(3)按照数理统计方法分析指标间的互相关性，计算结果见表2。从表2可以看出，6项指标相互关联，指标间均为正相关，达到高度(相关系数0.9以上)、中度相关。

图4　总体样本统计情况

ln(Y1)ln(Y2)ln(Y3)ln(Y4)ln(Y5)ln(Y6)F1F2ln(Y1)1.00000.80070.99690.93920.70830.67810.3951-0.5346ln(Y2)0.80071.00000.83470.95210.95990.92890.42250.2409ln(Y3)0.99690.83471.00000.95950.74530.71010.4047-0.4724ln(Y4)0.93920.95210.95951.00000.88680.84200.4305-0.1393ln(Y5)0.70830.95990.74530.88681.00000.92790.40330.4233ln(Y6)0.67810.92890.71010.84200.92791.00000.39210.4842贡献率88.279.8292

图5　第一主成分、起伏高差之对数与桥隧比的分布关系

(4)在各项指标标准化处理后进行主成分分析(其计算结果见表2)。第一、第二主成分贡献率达98.1%，其中第一主成分贡献率就达88.3%。在第一主成分中，6项指标荷载系数相差不大，表明该6项指标在描述线路纵断面起伏特征时具有相当的作用。

3　地面起伏高差与线路工程特征关系的研究

取“某一长度”为2 km，计算出沿线地面起伏高差数值指标及其相应桥隧比。

由于第一成分是折算指标，实际中并没有直观的反映，相反，实际工作中更喜欢采用地面起伏高差Y1来反映线路工程特征。本文在研究第一成分与桥隧比的关系时，同时研究起伏高差平均值与桥隧比的关系。根据收集到的线路纵断面，其计算结果如图5所示。

从图5可以看出：

(1)第一主成分F1与桥隧比之间没有一一对应关系，虽然两者分布凌乱但有相对稳定的变化趋势。平均意义上来看，随着F1的加大，桥隧比也增加，基本呈线性规律。

(2)用数学的方法表示，ln(Y1)与桥隧比之间也没有一一对应关系，两者分布也比较凌乱，也有相对稳定的变化趋势。平均意义上来看，随着ln(Y1)的加大，桥隧比也增加，大致呈线性规律。

(3)在相同的F1或ln(Y1)条件下桥隧比变化幅度也比较大，这反映出线路纵断面起伏高差特征并不是桥隧比的决定因素，与相应范围的自然因素、人文因素、设计因素等有重要的关系。但在一定范围内，线路纵断面起伏高差仍然是桥隧比的主要因素之一。

4　单位长度选取的影响分析

受统计的多元影响，如果“某一长度”取得过小，在该长度范围内的样本数量过小，将直接影响数据的统计结果，“某一长度”取得过大，又不能反映局部变化的真实状态。为此，研究单位长度的取舍是非常必要的。选取不同“某一长度”，主要的计算结果见表3。

表3　第一主成分、ln(Y1)与桥隧比的关系

选取某一长度为6 km，则第一主成分F1=0.405 35ln(Y1)+0.413 74ln(Y2)+0.413 35ln(Y3)+0.414 28ln(Y4)+0.402 95ln(Y5)+0.399 57ln(Y6)≈0.4082[ln(Y1)+ln(Y2)+ln(Y3)+ln(Y4)+ln(Y5)+ln(Y6)]，表现为六项指标同等重要。桥隧比=12.46F1+58.64，即桥隧比≈12.46∑(ln(Y0.408 2))+58.46。

5　地面起伏高差与地形等级初探

实际工作中，习惯把地形划分为等级，从而反映铁路工程的艰巨程度，侧面反映铁路工程规模或造价。如果采用第一直观的感觉概略估计桥隧比，可以引用Y1，则桥隧比=27.11ln(Y1)-31。概略地形等级、起伏高差、桥隧比重见表4。

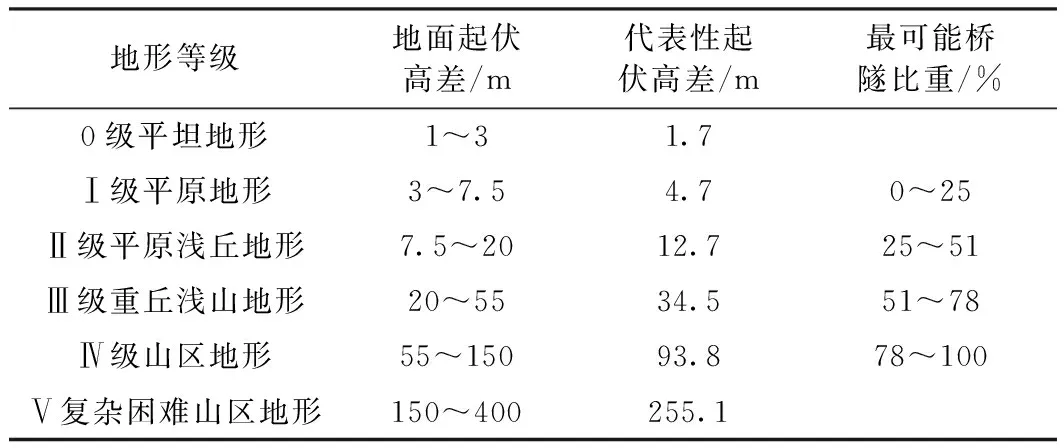
表4　地形等级与桥隧比的关系

6　结论与展望

(1)地面起伏高差与线路工程桥隧比之间有着密切的关系，其关系不是一一对应关系。

(2)以6～10 km范围内地面起伏高差的各项统计指标，经过主成分分析可以更有效地分析工程规模。

(3)以地面起伏高差或其各项统计指标构成的主成分作为连续变量，能够快速计算线路的工程规模。

(4)结论可拓宽到线路平纵断面，能有效提高概略选线效率。

[1]蒲俊，等.MATLAB6.0数学手册[M].上海：浦东电子出版社,2002

[2]费业泰.误差理论与数据处理[M].北京:机械工业出版社,2000

[3]徐建华.现代地理学中的数学方法[M].北京:高等教育出版社,2002

[4]隋刚.利用高程标准差表达地形起伏程度的数据分析[J].太原理工大学学报，2010，41(4)

[5]焦艳龙.Matlab在土工试验数据分析中的应用[J].铁道勘察,2014(5)

[6]谢卫民.山西中南部铁路太岳山越岭方案研究[J].铁道勘察,2010(3)

[7]康荣良.客运专线高填方路基改为桥梁设计有关问题的探讨[J].铁道勘察,2007(1)

Discussion on the Relationship Between the Ground Fluctuation Characteristics and the Scale of Railway Engineering

ZHAO JinshunPENG Jiansuo

2016-01-20

赵金顺(1964—)，男，2008年毕业于北京交通大学道路与铁道工程专业，博士，教授级高级工程师。

1672-7479(2016)02-0078-04

TB114

A