考虑非比例阻尼的基础隔震结构非线性反应谱研究

杜永峰，徐天妮，包　超，陈　凯，洪　娜

(1 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州　730050；2 兰州理工大学 防震减灾研究所，兰州　730050)



考虑非比例阻尼的基础隔震结构非线性反应谱研究

杜永峰1,2，徐天妮2，包超2，陈凯2，洪娜2

(1 兰州理工大学 西部土木工程防灾减灾教育部工程研究中心，兰州730050；2 兰州理工大学 防震减灾研究所，兰州730050)

对于基础隔震结构而言，其上部结构和隔震层的阻尼特性截然不同，往往呈现出明显的非比例阻尼特性。因此，有必要建立一种考虑非比例阻尼的隔震结构实用计算方法以便于推广和应用。通过用双自由度振动体系模拟基础隔震结构，在建立运动方程时考虑其非比例阻尼效应。通过对该简化模型进行动力时程分析，得到其在近场及远场地震记录作用下考虑非比例阻尼与瑞利阻尼的反应谱，并通过曲线拟合得到了非比例阻尼反应谱和瑞利阻尼反应谱的谱比值与结构自振周期之间的关系式。然后对某实际隔震工程进行地震响应分析，验证所提公式的合理性。

非比例阻尼；反应谱；近远场地震记录；基础隔震结构

隔震技术自20世纪末以来，已成为国内外结构工程和防灾领域的热点研究方向[1]。反应谱是目前抗震设计中应用最广泛的确定地震作用的理论依据，其应用在很大程度上简化了结构的抗震设计计算，在其70多年的发展过程中，基础隔震结构的反应谱研究也取得了很大的进展[2-5]。

阻尼是结构抗震分析中的一个重要因素，也是结构的动力特性之一，对于由同种材料组成的结构，目前公认其阻尼处于某一范围，我国规范规定混凝土结构阻尼比取0.05，钢结构取0.02，而基础隔震结构中的隔震层与上部结构的阻尼特性是截然不同的，往往体现出非比例阻尼特性，因此用某一定值显然不能反应结构的耗能特点[6]，故国内外学者提出了非比例阻尼这一特殊议题，并作了大量的研究[7-12]，其中，RYAN[13]指出在动力分析中，基础隔震结构利用经典阻尼求解会使分析结果不合理。

作为研究所针对的基础隔震结构，前人对隔震层非比例阻尼特性已做了大量的研究，但是对于考虑这一特性来分析隔震结构的反应谱的研究还不是很多。现有规范[14]的设计反应谱通过对阻尼比为0.05的标准反应谱进行修正，得到了不同阻尼比情况下的设计反应谱，但是基础隔震结构的隔震层与上部结构的阻尼比是不一致的，为得到精确分析与设计结果，有必要在研究反应谱时考虑非比例阻尼因素。

选取ATC-63[15]建议的地震记录作为激励，并将基础隔震结构简化为两自由度体系，采用分区瑞利阻尼模型，利用状态空间法，对基础隔震结构进行时程分析，求出结构在地震作用下的时程反应，并得到其反应谱。通过对比分析分别考虑非比例阻尼和比例阻尼时反应谱的特性，建立了二者与结构自振周期之间的关系，并给出了拟合公式，其形式简单，计算方便，适于工程应用。文中最后通过数值算例验证了所提公式的有效性。

1　基础隔震结构的反应谱

1.1双自由度体系运动方程

地震作用下两自由度体系的运动方程为：

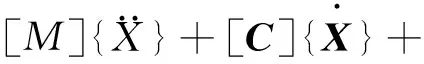
[K]{X}〗

(1)

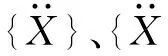
由于隔震层与上部结构的阻尼明显不同，所以其阻尼矩阵与经典阻尼体系的阻尼也不相同，引用分区瑞利阻尼模型，即非比例阻尼的表达式为：

[C]=[C0]+[Cr]

(2)

式中:[C0]是瑞利阻尼矩阵，其表达式为

[C0]=αs[M]+βs[K]

(3)

[Cr]为非比例阻尼的余项阻尼矩阵，其表达式为

式中，αt、βt、αb、βb分别是上部结构和隔震层的瑞利阻尼比例系数，mb、kb分别为隔震层的质量与等效刚度。

1.2基础隔震结构的反应谱分析方法

利用状态空间法时，上部结构与隔震层的阻尼比分别取0.05、0.20，式(1)可表示为：

(5a)

(5b)

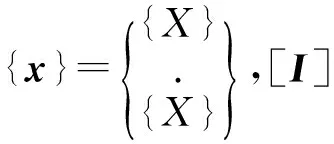
1.3地震记录的选取

从美国太平洋地震中心(PEER)强震数据库中选取了ATC-63报告建议的21条远场水平向强震记录和23条近场水平向强震记录，见表1。所选地震记录的PGA均大于0.2 g，PGV均大于15 cm/s；地震记录的有效周期至少达到4 s，且所有的地震记录均为岩石或硬土场地条件下的地震记录。

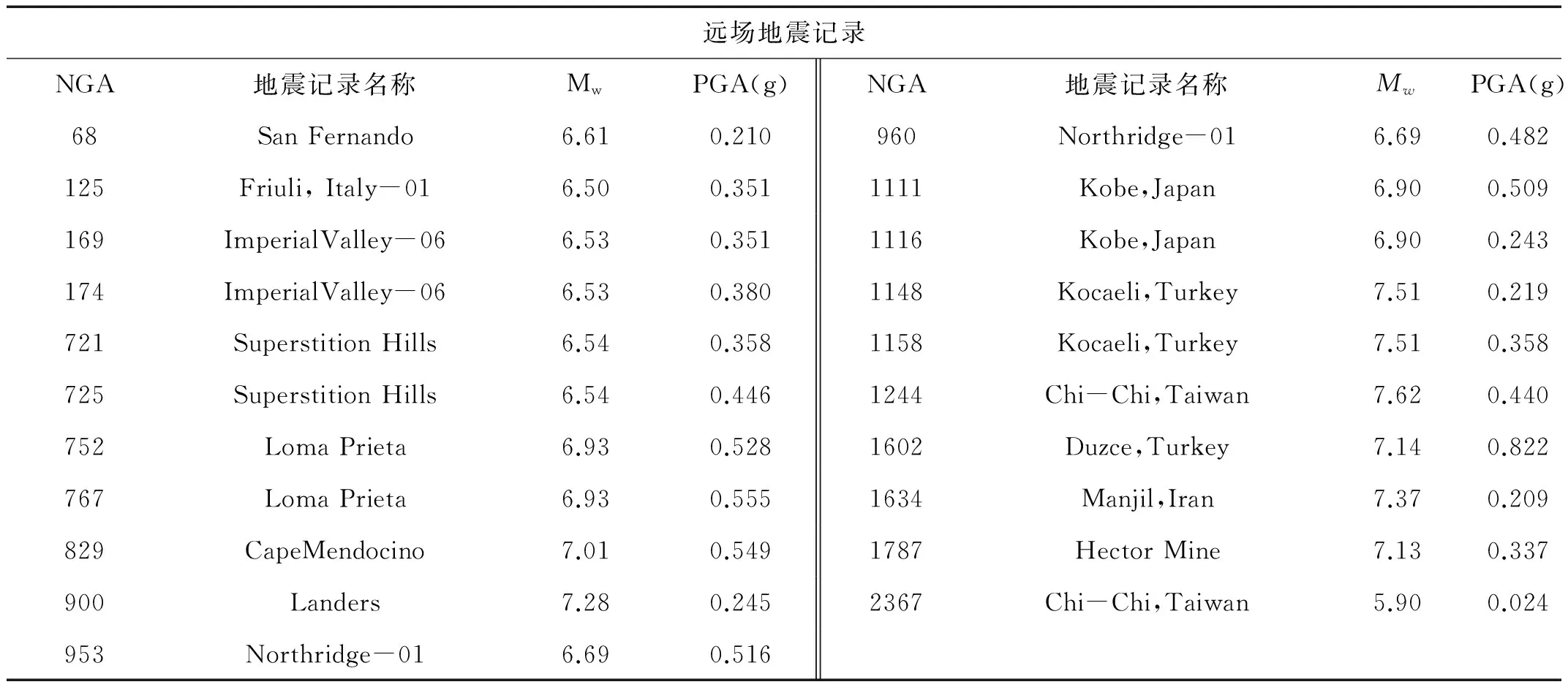
表1　远场地震记录

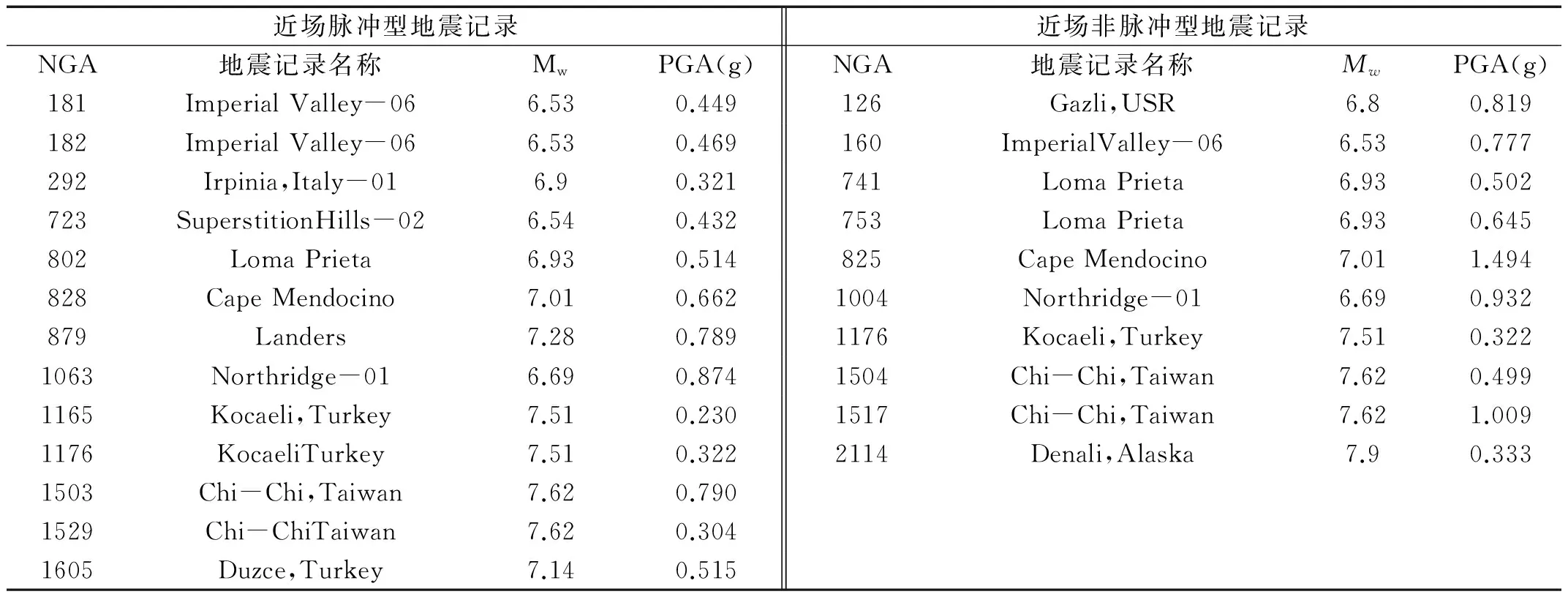
表2　近场地震记录

2　基础隔震结构的反应谱对比分析

在建立结构的反应谱时，假设上部结构与隔震层的阻尼比均为一定值，隔震结构自振周期T的取值从0.02 s到10 s，间隔0.02 s，用表1中的地震记录进行地震响应分析，最终得到基础隔震结构的位移反应谱、加速度反应谱及其平均反应谱，见图1。

图1表示三种不同类型的地震作用下，隔震结构的位移反应谱及加速度反应谱，从图中给出的平均反应谱曲线(粗虚线)可以发现，无论考虑非比例阻尼与否，反应谱的谱形规律都是相似的，均包含上升段、峰值、下降段，水平段，这与规范中反应谱谱形是基本一致的。隔震结构自振周期较小时，响应随着其周期的增加而增大，但当达到某一定值后，响应不再随其周期的增大而变化或者变化很小。

当隔震结构自振周期小于4 s时，阻尼会对其反应谱曲线产生明显的影响，即考虑非比例阻尼后隔震结构的响应都偏大。从图1的平均反应谱可以看出，远场地震作用下，考虑非比例阻尼后结构的位移、加速度响应与仅考虑瑞利阻尼时相比最大分别增加了36.7%、40.4%；同样地，近场脉冲型地震作用下结构的位移与加速度响应最大分别增加了34.7%、34.4%；近场非脉冲型地震作用下结构的位移与加速度响应最大分别增加了33.9%、33.6%。

图1　地震作用下结构的位移谱及加速度谱Fig.1　The displacement spectra and acceleration spectra under ground motions

在实际的设计和评估时都有满足保守估计的要求，因此，在传统的抗震设计中，基础隔震结构的抗震设计是需要考虑其非比例阻尼特性的，若不考虑，使计算得到的结果偏小就不能满足保守估计的要求。另外，抗震规范规定，隔震结构不阻碍隔震层在罕遇地震下的大变形的措施之一为：上部结构的周边应设置竖向隔离缝，缝宽不宜小于各隔震支座在罕遇地震下的最大水平位移值的1.2倍且不小于200 mm。因此，若按传统的抗震设计方法设计隔震结构，没有考虑隔震层的非比例阻尼特性，得到的隔震层水平位移就会偏小，隔震缝的尺寸相应偏小就可能会使隔震层的水平变形受到阻碍，在罕遇地震下不仅不能起到隔震的效果，反而会使隔震结构破坏。

从图1中的平均反应谱可以看出，隔震周期大于4 s后，考虑非比例阻尼的谱值比比例阻尼的谱值小，这是因为考虑非比例阻尼后，长周期段结构累积的阻尼耗能较不考虑时大，刚度自然就变小，而在输入同等的地震能量的情况下，较小刚度隔震层的滞回耗能较大，那么结构的响应自然就会较小。但是一般的基础隔震结构周期都在图中所示的短周期段，说明在进行隔震结构的抗震设计时，用传统的反应谱计算得到的地震作用、位移都偏小。

3　非比例阻尼反应谱与瑞利阻尼反应谱关系

从前面的分析可知，非比例阻尼对结构反应谱会产生一定的影响，为了使得基础隔震结构的抗震设计在合理的基础上得到简化，现根据非线性曲线拟合方法，给出考虑非比例阻尼的反应谱(Snpd)与考虑瑞利阻尼的反应谱(Spd)的谱比值(称之为反应谱比谱)与结构自振周期关系的拟合表达式，利用该表达式可以直接在比例阻尼得到的结构反应谱的基础上获得考虑非比例阻尼的结构反应谱，便于工程实际应用，该表达式为：

Snpd/Spd(T)=aTb+c

(6)

式中:T为隔震结构的自振周期，a,b,c为表达式的相关参数，它们的取值与地震记录的类型及反应谱的类型有关，见表3，表中列出了不同地震记录和反应谱类型的对应拟合表达式的相关参数取值，在估算考虑非比例阻尼特性的基础隔震结构响应时，可以通过查表来得到所需的取值。

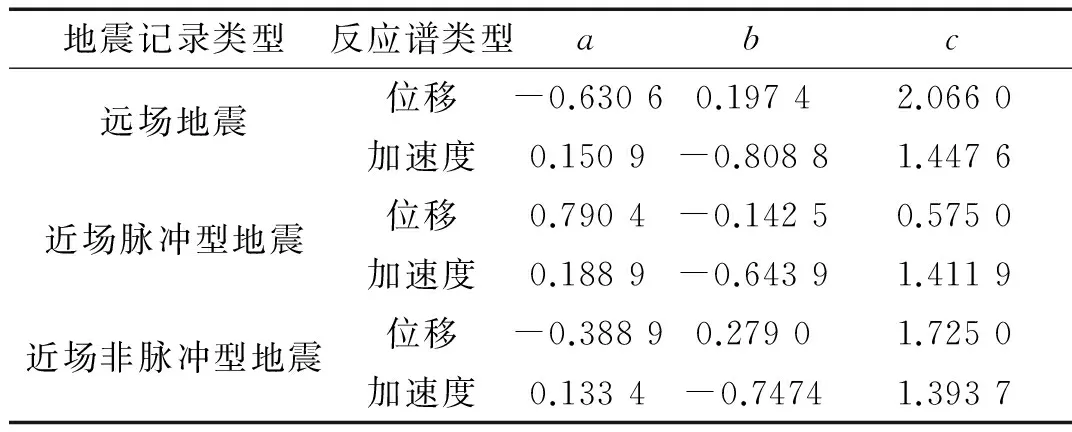
表3　拟合表达式的参数取值

图2所示为反应谱比谱与通过曲线拟合得到的拟合曲线。从图中可以看出，对于任意一类的地震记录，通过拟合表达式得到的拟合曲线与真实的反应谱比谱之间的匹配度还是比较高的，说明文中给出的拟合表达式具有一定的准确性。

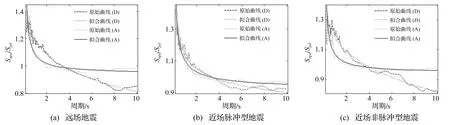
图2　不同地震记录作用下反应谱比谱及其拟合曲线Fig.2　Ratio spectra and its fitting curve under different ground motion

4　算例分析

以某上部结构8层的基础隔震结构为例[16]，进行时程分析。具体参数为：上部结构质量mi=2.3×105kg(i=1,2…，8)，刚度ki=2.3×108N/(i=1,2…，8)；隔震层质量mb=3.3×105kg，隔震层的总刚度kb=1.92×105N/m，隔震支座的屈服位移dy=0.015 m，隔震支座的极限位移du=0.33 m，隔震支座屈服后与屈服前的刚度比α=0.1，可以得到隔震层的等效刚度keq=2.679×106N/m，隔震结构的设计基本周期Tb=2.24 s。

4.1时程分析地震记录

在三种类型的地震记录中各选取三条不同的地震记录，如表4。

表4　时程分析选用的地震记录

4.2基础隔震结构时程分析

由时程分析可得到各时程的最大值，列于表5中，从表中可以看出，无论是哪种类型的地震作用，按非比例阻尼计算的结构响应均大于按比例阻尼计算的结构响应，位移响应的增加了13%～52%，加速度响应的增加了27%～134%，这就意味着在抗震设计中，工程设计人员考虑的峰值位移、基底剪力都是偏小的。

该隔震结构的自振周期Tb=2.24 s，结构响应如表5所示，将这些数据代入式(6)中，可得出不同类型地震作用下考虑非比例阻尼的反应谱与考虑瑞利阻尼反应谱之间的比值，并与时程分析结果进行对比，得到二者之间的相对误差，见表6，并验证所得到公式的合理性。

从表中可以看出，拟合表达式能较好地反映结构的响应，说明该拟合表达式具有一定的准确性。

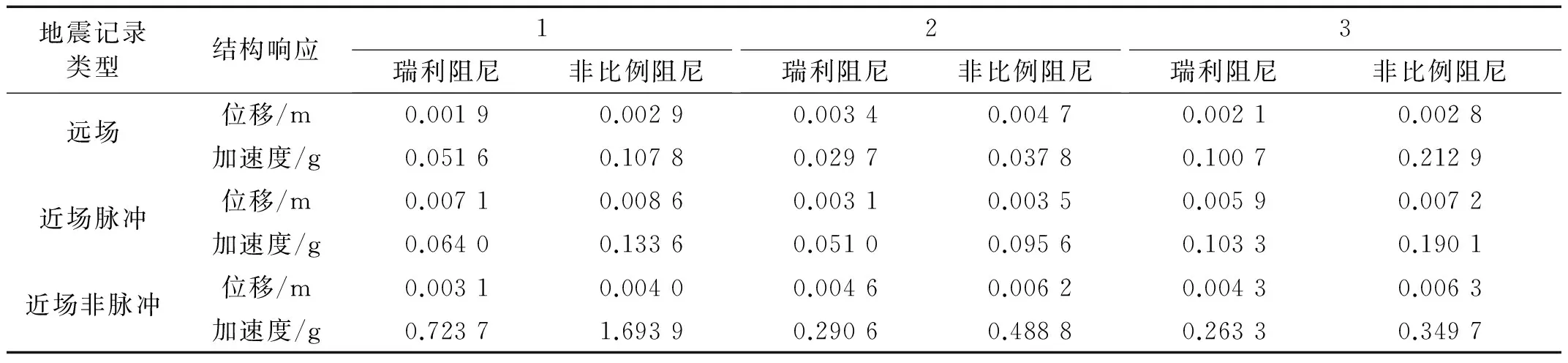
表5　结构的响应

表6　拟合表达式与结构响应对比

5　结　论

通过研究基础隔震结构非比例阻尼特性对其反应谱的影响，得到以下一些结论：

(1)不同类型的地震记录作用下，考虑非比例阻尼特性后，结构的位移响应、加速度响应均有所增加，增加约为30%。

(2)隔震结构自振周期在0～4 s时，其抗震设计需要考虑隔震层的非比例阻尼特性，可使得设计满足保守估计的要求；但一旦隔震结构自振周期大于4 s，则不宜再采用非比例阻尼反应谱。

(3)通过曲线拟合给出谱比值与隔震结构自振周期之间的关系表达式具有一定的合理性。在实际工程应用中，通过相关参数的取值，可以在瑞利阻尼结构响应的基础上快速得到具有非比例阻尼特性的结构响应，为隔震结构的初步设计提供依据。

由于建立的模型较单一，因此拟合关系式仅适用于上部结构较规则的基础隔震结构，对于上部结构复杂或其他类型的隔震结构的设计计算，仍需作进一步的研究。

[1]周福霖.工程结构减震控制[M].北京:地震出版社,1997.

[2]施卫星,李正升.基础隔震结构设计反应谱[J].工程力学,1998(增刊1)115-120.

SHI Weixing,LI Zhengsheng.Design spectra of base-isolated structures[J].Engineering Mechanics,1998(Sup1)115-120.

[3]周云,安宇,梁兴文.基础隔震结构基于位移的设计方法[J].广州大学学报(自然科学版),2002,1(1):75-79.

ZHOU Yun,AN Yu,LIANG Xingwen.A based-displacement design method of base-isolated structures[J].Journal of Guangzhou university(Natural Science Edition),2002,1(1):75-79.

[4]曹加良,刘文光,何文福.基础隔震结构反应谱拟谱与真谱差异研究[J].世界地震工程,2009,25(2):76-80.

CAO Jialiang,LIU Wenguang,HE Wenfu.Studies on differences between pseudo and real response spectra of base-isolated structure[J].World Earthquake Engineering,2009,25(2):76-80.

[5]王涛,王飞,候钢领,等.核电厂隔震结构的振动台试验研究[J].工程力学,2014,31(10):62-69.

WANG Tao,WANG Fei,HOU Gangling,et al.Shaking table test on base-isolated nuclear power plant[J].Engineering Mechanic,2014,31(10):62-69.

[6]周国伟,张志强,李爱群,等.混合结构时程分析中的阻尼比计算研究[J].振动与冲击,2012,31(16):117-122.

ZHOU Guowei,ZHANG Zhiqiang,LI Aiqun,et al.Damping ratio of composite structures used in time-history analysis [J].Journal of vibration and shock,2012,31(16):117-122.

[7]张树传,何玉敖,王亚勇.非比例阻尼线性体系振型组合法适用范围探讨[J].建筑结构,2011,41(5):63-67.

ZHANG Shuchuan,HE Yuao,WANG Yayong.Discussion on application scope of mode combination method for non-classically damped linear system [J].Building Structure,2011,41(5):63-67.

[8]杨志勇,李桂青,瞿伟廉.结构阻尼的发展及其研究近况[J].武汉工业大学学报,2000,22(3):38-41.

YANG Zhiyong,LI Guiqing,QU Weilian.The research history and recentdevelopment of structural damping [J].Journal of Wuhan University of Technology,2000,22(3):38-41.

[9]李田.结构时程动力分析中的阻尼取值研究[J].土木工程学报,1997,30(8):68-73.

LI Tian.A study on damping values applied to the time-history dynamic analysis of structures [J].China Civil Engineering Journal,1997,30(8):68-73.

[10]黄宗明,白绍良,赖明.结构地震反应时程分析中的阻尼研究[J].土木工程学报,1998,31(2):75-79.

HUANG Zongming,BAI Shaoling,LAI Ming.An investigation of damping in earthquake response time-history analysis of structures[J].China Civil Engineering Journal,1998,31(2):75-79.

[11]KELLY J M.The role of damping in seismic isolation [J].Earthquake Engineering and Structure Dynamic,1999,28(1):3-20.

[12]TSAI H C,KELLY J M.Seismic response of heavily damped base isolationsystems [J].Earthquake Engineering and Structure Dynamic,1993,22:633-645.

[13]RYAN K L,POLANCO J.Problems with rayleigh damping in base-isolated buildings[J].Journal of Structure Engineering,2008,134(11):1780-1785.

[14]建筑抗震设计规范:GB 50011—2010[S].中华人民共和国住房和城乡建设部,2010.

[15]ATC-63(2006).International Building Code[S].International Code Council,2006,USA.

[16]李慧,王亚楠,杜永峰.近场地震作用下TMD-BIS混合控制体系的非线性响应分析[J].土木工程学报,2013,46(增刊1):57-62.

LI Hui,WANG Yanan,DU Yongfeng.Seismic response analysis for nonlinear base-isolated structure with TMD under near fault ground motion [J].China Civil Engineering Journal,2013,46 (Sup1):57-62.

Nonlinear response spectra for base-isolated structures with non-proportional damping

DU Yongfeng1,2,XU Tianni2,BAO Chao2,CHEN Kai2,HONG Na2

(1.MOE Western Engineering Center of Disaster Mitigation in Civil Engineering,Lanzhou University of Technology,Lanzhou 730050,China;2.Institute of Earthquake Protection and Disaster Mitigation,Lanzhou University of Technology,Lanzhou 730050,China)

The damping characteristics of upper structure and isolation layer for a base-isolated system are completely different,so the system often exhibits significant non-proportional damping characteristics.It is necessary to consider the non-proportional damping during aseismic design of base-isolated structures.Meanwhile,this design method is convenient for promotion and application.Here,a 2-DOF simplified model for base-isolated structures was set up,and the non-proportional damping effect was considered to establish the dynamic equation of the system.Then,the responses of the simplified model were analyzed and its response spectra considering non-proportional damping and Rayleigh damping,respectively under the excitation of near-field and far-field ground motions.The calculation formulas for the ratio of its non-proportional damping response spectra to its Rayleigh damping ones and the system’s natural vibration periods were deduced wth the curve-fitting method.Finally,the seismic response analysis for a real base-isolated structure was performed,and the reasonableness of the proposed formulas.

non-proportional damping; response spectra; near-filed and far-filed ground motion records; base-isolated structure

国家自然科学基金资助项目(51178211)

2015-06-05修改稿收到日期：2015-08-29

杜永峰 男，博士，教授，博士生导师，1962年生

TU311.3

A DOI:10.13465/j.cnki.jvs.2016.17.035