球壳在可压缩空气下的耦合振动分析
刘 平,付功义
(1.江苏科技大学 土木工程与建筑学院,江苏 镇江 212003;2.上海交通大学 船舶海洋与建筑工程学院,上海 200240)
球壳在可压缩空气下的耦合振动分析
刘平1,付功义2
(1.江苏科技大学 土木工程与建筑学院,江苏镇江212003;2.上海交通大学 船舶海洋与建筑工程学院,上海200240)
大跨空间结构近年来应用越来越广,此类结构对于风荷载十分敏感。如何考虑空间结构与空气耦合振动作用成为业界难点。通过对三维球形结构在可/不可压缩空气下振动问题进行分析,在假设边界为简谐振动并忽略低阶项的情况下,求解出两种情况下的理论解。结合具体的物理模型,对理论结果进行了探讨,得出以下结论:不可压缩假设下,结构表面压力值主要部分与振动加速度及结构曲率半径成正比,流场对结构作用力相当于附加质量;而在可压缩空气情况下,压力值与振动速度成正比、与结构形式无关,流场对结构作用力可相当于黏滞阻尼。最后,利用数值方法对理论解进行了验证,结果符合良好。结果可以推广到壳形结构,为大跨空间结构的抗风、抗振提供理论支持。
可压缩流体;空间结构;耦合振动
大跨空间结构是近年来发展最快的结构形式[1],被广泛应用于体育场馆、会展中心、影剧院等大型公共建筑中[2-3]。空间结构在力学表现上具有许多不同于传统刚性结构之处[4-5]:与空气的相互作用是其设计中的控制因素。结构振动带动周围空气运动,而空气运动同样影响结构的振动,这种相互影响、相互作用,形成典型的流固耦合现象[6-7]。由于这种耦合振动的强非线性,其理论求解十分困难,同时也一直受到国内外广大学者的普遍关注。IWIN等[8]在研究蒙特利尔体育馆气动弹性模型的风洞试验中,给出了一个可供工程使用的附加质量计算公式。MINAMI[9]根据势流理论,假设结构振型为正弦、做简谐振动情况下,推导出矩形平面结构在空气中的附加质量。而王吉民[10]在假设结构振型为二次函数,也提出了结构的附加质量公式。YADYKIN等[11]利用数值方法,研究了薄板在流场中振动的附加质量。何艳丽[12]利用弱耦合方法对充气膜与空气的耦合效应进行了分析。孙芳锦[13]利用广义极小残余法(Generalized Minimum Residual)应用于强耦合方法中,研究了风与空间结构的流固耦合效应,结果表明,此方法能够有效提高计算效率。
但是,不管是理论分析还是数值方法,对于空气(流体)均采取不可压缩假设,此项假设简化了数学求解的难度,却改变了问题的物理规律:振动对空气的影响瞬时传递到整个流场,而实际,结构振动对于流场是以有限速度传播。本文以球形结构与空气耦合振动为研究对象,考虑到空气可压缩性,探讨流场速度与结构表面压力在耦合振动时的变化规律。这此规律可以推广到壳形结构的振动中,对工程实践具有一定的应用价值。
1 控制方程与求解
设有一球形结构在半径方向做均匀振动(见图1圆,表示相同半径的球),考虑对称性、假设无粘流体,控制方程见式(1)。显然,结构振动为流场运动边界、流场边界压力反作用于结构,耦合方程可简化为[14]:
(1)
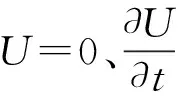
初始条件为:t=0时,有:u=0、ρ=ρ0、p=p0。
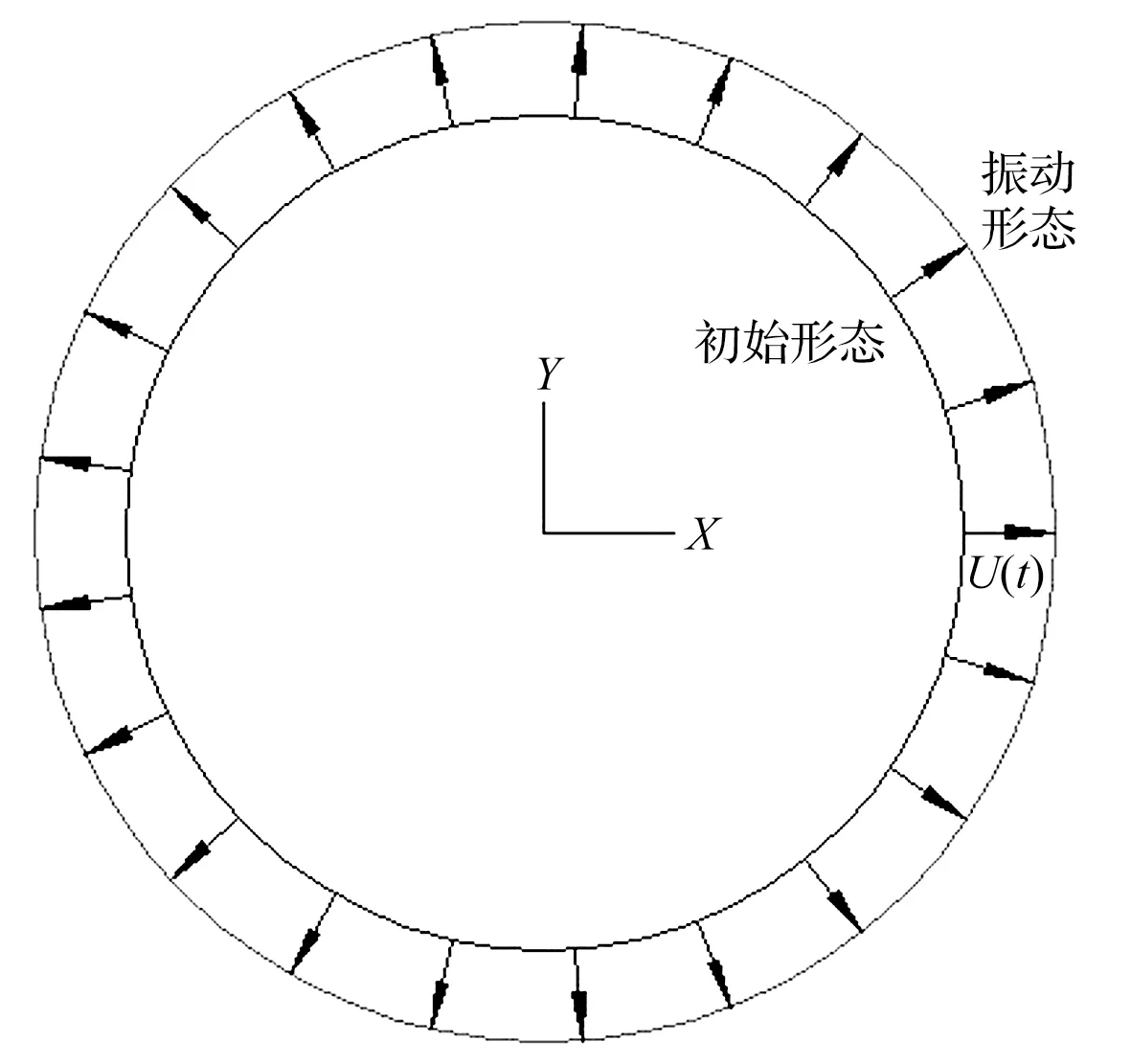
图1 球形可压缩流体振动示意图Fig.1 The figure ofsphere vibration of structure
1.1可压缩方程流体方程求解
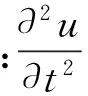
(2)
由式(2)可知,密度变化由两项组成:流体速度随时间改变量及随位置改变量之和。忽略第二项,即迁移加速度,将密度解代入式(1)中连续性方程(第二项),有:
忽略密度变化,并由速度作简谐运动,方程可化为:
(3)
将方程式(3)各项对r求导,有:

(4)
此即为典型的一阶球类Bessel函数,其解为:u=Aj1(s)+By1(s),其中A、B为时间t的函数;j1(s)、y1(s)分别为一阶的第一类、第二类球Bessel函数。当r=rs时,有:us(t)=Aj1(sr)+By1(sr);当r→∞时,边界条件自动满足。
由于假设u为频率为ω的简谐函数,故可知A、B同样为简谐函数。因此则可设A=Ccos(ωt+φ)、B=Csin(ωt+φ),C、φ为常数,(注:若假设A=Csin(ωt+φ)、B=Ccos(ωt+φ)可得出同样结果),由边界速度与指定速度恒等,可以确定常数C、φ。
另外,从求解过程可以看出,忽略非线性项的情况下,方程为线性方程,因此,对于非简谐振动情况下,可以先把振动函数用简谐函数展开,再利用本文所述方法求解。
1.2流场速度分析
将A、B设定为简谐函数并代入边界条件有:
us=C[cos(ωt+φ)j1(sr)+sin(ωt+φ)y1(sr)]=
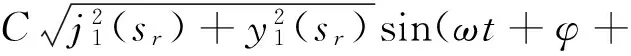
由Bessel函数性质可知,当s较大时[15-16]:
代入解并化简后,有:
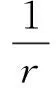
1.3流场压力分析

ΔP=
s、φ值见上节。
与上节相同,当s较大时,有
代入ΔP,原式有:
(5)
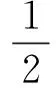
1.4不可压缩流体方程求解
作为对比,假定空气不可压缩,则控制方程为:

结构边界条件如上节1.1,流场边界条件为:r=rs时,有:u=us(t);远场边界条件r=R时,有:p=p0。
代入远场边界条件,故可得:
(6)
1.5方程解讨论
对于不可压流体,由式(6)可以看出,采取不可压缩假设与否对于结果有重要影响。在不可压缩假设下,压力值来源于两部分:第一项为流体随时间加速度影响值,与边界加速度成正比且与流场区域长度成反比;第二项为流体随空间加速度值,与边界振动速度的平方正比、与半径的四次方成反比。由式(6)可以看出,边界压力值随着外流场区域(R值)的增大而缓慢减小,这种规律表明对于数值求解而言,取一定大小的外流场来模拟无穷远流场的流动,外流场对结果的影响可以忽略。
而对于可压缩流体,由式(5)知,Δp=ρocu,其值与边界振动速度成正比,比值为声速与密度的乘积。在这种情况下,由式(1)中第一式知道,流场对结构的作用相当于粘滞阻尼,阻尼系数为定值。
2 数值验证
为直观验证上述理论解的正确性,对球状可压缩空气模型与不可压缩空气模型进行了数值模拟。模型边界球半径为10 m、远场半径为500 m(可参考图1),入口速度取u=sin(10t)、出口设为压力远场,参考压力设为0;其余设为光滑壁面;计算时间为1 s、时间步为0.005 s。可压缩采用理想、无粘空气模型,声速c=340 m/s;不可压缩采用无粘、恒密度空气模型。
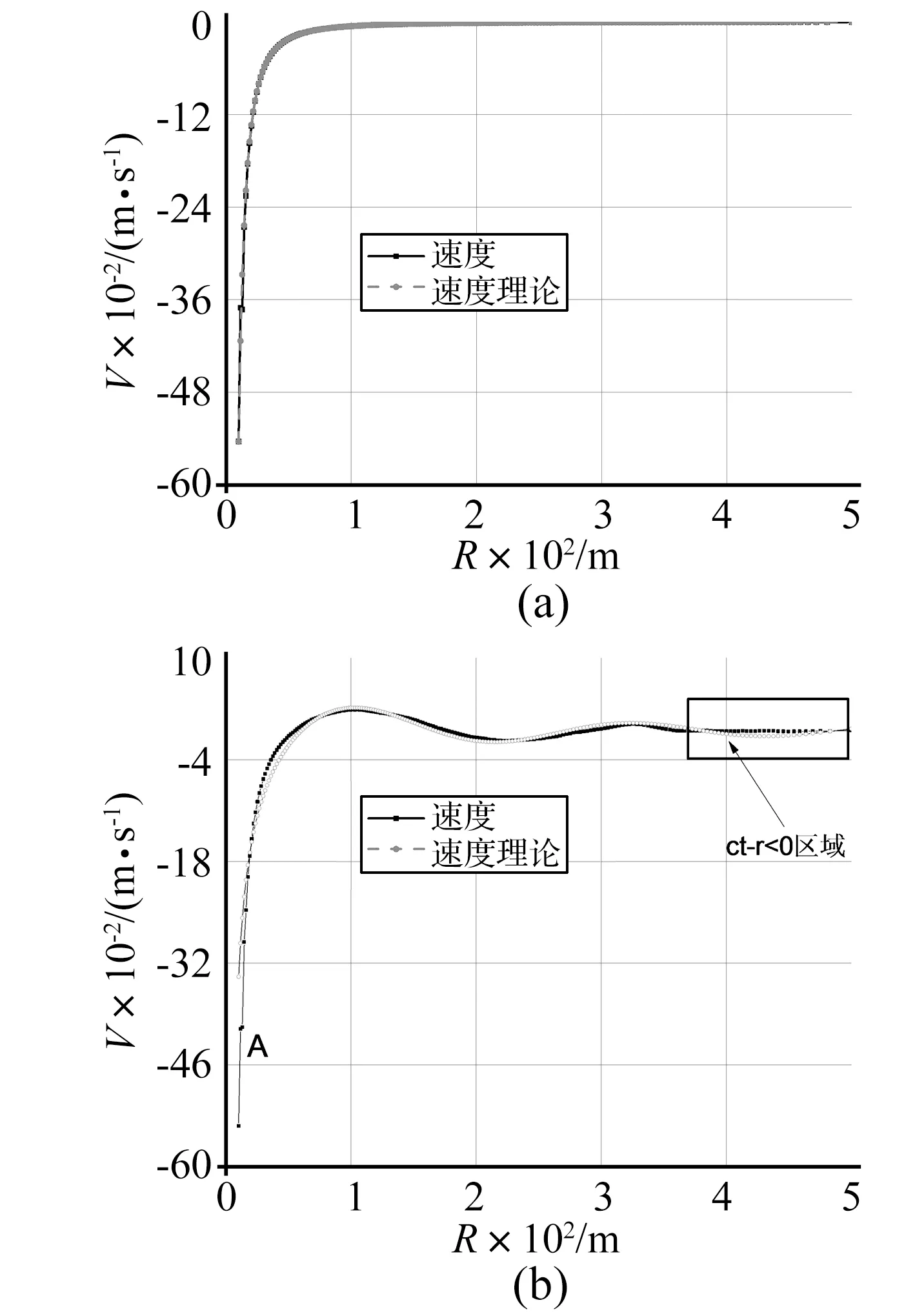
图2 t=1 s时不可压缩、可压缩假设下流场速度理论值与数值解比较Fig.2 The fig of velocity to Radius in in-compressive and compressive flow when t=1 s
图2(a)和(b)所示分别为t=1 s时不可压缩/可压缩假设下流场速度理论解、数值解与半径关系图。从图2(a)可以看出,理论解与数值解符合得很好。从理论解可以看出,不可压缩假设下,边界运动瞬间传递到整个流场域;而可压缩情况下,边界运动需要经过一段时间才能传递到远场。由于在将球类Bessel函数近似于三角函数时,r值越小、误差越大,因此,图2(b)A点处,理论值与数值解有较大差异。另外,图2(b)中,在距离ct≤r处出现了较大的差异,数值解基本为零,而理论解有较小的数值,即图2矩形框中所示。这是因为在ct≤r区域,流场在边界振动的影响区域之外,处于静止状态,图中为了显示简洁,理论解没有截断。
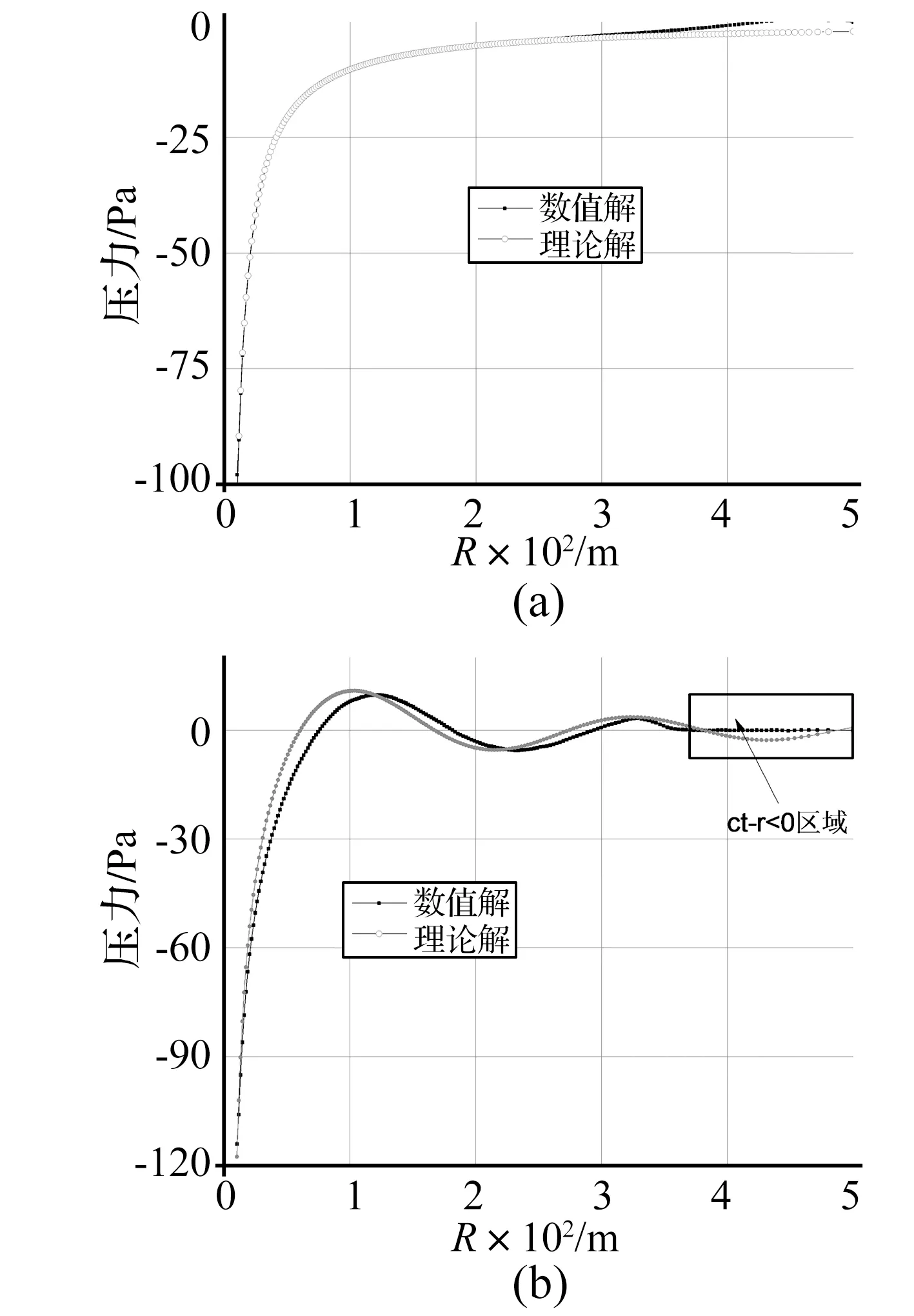
图3 不可压缩、可压缩假设下压力数值解与理论解比较Fig.2 The fig of pressure to Radius in in-compressive and compressive flow when t=1 s
图3(a)和(b)所示分别为t=1 s时不可压缩与可压缩假设下压力值的理论解与数值解比较。从图中可以看出,理论解与数值解符合良好。尤其是对于不可压缩情况,数值解与理论几乎完全相同;在可压缩情况下,数值解与理论解在边界附近数值几乎一致,在影响区域最远端误差较大。图3(b)在ct≤r区域结果误差较大的原因与上同。
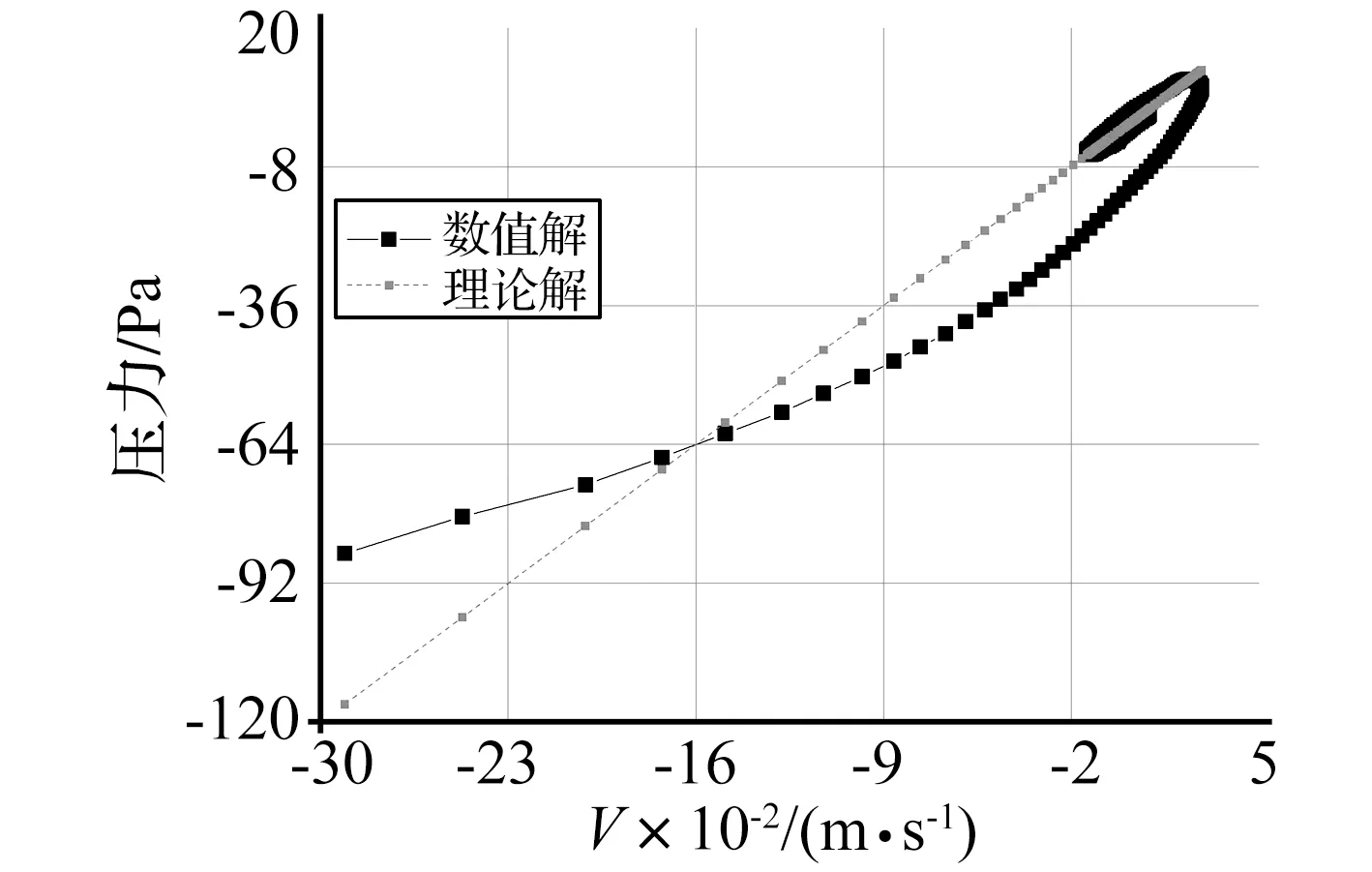
图4 可压缩下速度-压力数值解与理论解比较Fig.4 The fig of velocity-pressure in compressive flow
图4所示为可压缩下速度与压力数值解与理论解比较。理论解预测压力与速度成正比,比值为ρ0c=417,图中一次曲线拟合曲率为400,符合预期。不过,由于Bessel函数在r较小时,以三角函数近似误差较大,同时,r离边界越近、速度越接近边界运动速度,因此速度-压力数值解与理论值的误差也越明显。
3 结 论
通过对一维结构在空气中的振动问题进行理论分析,在舍弃低阶项的情况下分别求解出空气不可压缩与可压缩情形下的理论解。对比理论结果,得出以下结论:
(1)不可压缩假设下,结构边界压力值由两部分组成:随时间加速度改变量与随空间加速度改变量。随时间改变量与振动加速度及边界半径成正比;而随空间加速度与振动速度的平方成正比;可压缩空气下,边界压力值与边界振动速度成正比、与流场长度无关;
(2)而在可压缩空气下,流场对结构作用相当于粘滞阻尼,阻尼系数为ρoc;不可压缩假设下,流场对结构作用随时间改变量相当于附加质量;
(3)不可压缩下,结构振动瞬间传递到远场,流速幅值与半径的平方成反比;在可压缩空气下,振动以空气声速向流场另一端传递,流速幅值与半径的一次方成反比。
[1]李元齐,胡渭雄,王磊.大跨度空间结构典型形体风压分布风洞试验研究现状[J].空气动力学学报,2010,28(1):32-38.
LI Yuanqi,HU Weixiong,WANG Lei.State-of-art:wind tunnel investigation on wind pressure distribution of large-span spatial structures with typical shapes[J].Acta Aerodynamica Sinica,2010,28(1):32-38.
[2]蔡丽.大跨空间结构抗风研究新进展与展望[J].黑龙江科技信息,2014(12):186.
CAI Li.New progress and prospect of study of wind resistance of large span space structure[J].Heilongjiang Science and Technology Information,2014(12):186.
[3]陈怡然,周岱,归洛圣.草帽型大跨空间结构的风压数值模拟与关键参数影响分析[J].振动与冲击,2013,32(15):37-40.
CHEN Yiran,ZHOU Dai,GUI Luosheng.Wind pressure simulation and key influence factors analysis of Mexico-Hat like spatial structures[J].Journal of Vibration and Shock,2013,32(15):37-40.
[4]柯世堂,葛耀君,赵林.一致耦合方法的提出及其在大跨空间结构风振分析中的应用[J].中南大学学报(自然科学版),2012,43(11):4457-4463.
KE Shitang,GE Yaojun,ZHAO Lin.Proposition and application of consistent coupling method in wind-induced response of long span structures[J].Journal of Central Sontral South Universtity(Natural Science Edition),2012,43(11):4457-4463.
[5]陈亚楠,周岱,孙颖昊.风敏感空间结构风致耦合研究与分析述评[J].振动与冲击,2012,31(7):104-112.
CHEN Yanan,ZHOU Dai,SUN Yinghao.The research of wind sensitive structures coupling with wind[J].Journal of Vibration and Shock,2012,31(7):104-112.
[6]王磊,李元齐,沈祖炎.薄膜振动附加质量试验研究[J].振动工程学报,2011,24(2):125-133.
WANG Lei,LI Yuanqi,SHENG Zuyan.Experimental investigation on the added mass of membrane vibration on air[J].Journal of Vibration Engineering,2011,24(2):125-133.
[7]LIU Z,ZHANG Q,LI H.Numerical simulation of fluid-structure interaction for the wind pressure distribution of membrane structure located horizontally[C]// The Fifth International Conference on Nonlinear Mechanics,Shanghai,2007.
[8]IRWIN H P A H,WARDLAW R L.A wind tunnel investigation of a retractable fabric roof for the montreal Onlympic stadium[C]//Proceedings of The 5th International Conference on Wind Engineering,Pergamon,1981.
[9]MINAMI H.Added mass of a membrane vibrating at finite amplitude[J].Journal of Fluid and Structures,1998,12:919-932.
[10]王吉民.薄膜结构的风振响应分析和风洞试验研究[D].杭州:浙江大学土木工程学院,2001.
[11]YADYKIN Y,TENETOV V,LEVIN D.The added mass of a flexible plate oscillating in a fluid[J].Journal of Fluids and Structures,2003,2003(17):115-123.
[12]何艳丽,沈继华.充气膜结构的流固耦合风效应分析[C]//第十四届空间结构学术会议,中国福建福州,2012[C].
[13]孙芳锦,张大明.基于预处理方法的风与膜结构流固耦合效应研究[J].地震工程与工程振动,2014(2):71-78.
SUN Fangjin,ZHANG Daming.Study on fluid-structure interaction of wind and membrane structure based on preconditioning[J].Earthquake Engineerig and Enginering Dynamics,2014(2):71-78.
[14]SCHOLCZ T P,VAN ZUIJLEN A H,BIJL H.Space-mapping in fluid-structure interaction problems[J].Computer Methods in Applied Mechanics And Engineering,2014,281:162-183.
[15]奚定平.贝赛尔函数[M].北京:高等教育出版社,1998.
[16]张善杰.矢量分析、圆柱函数和球函数[M].第1版.南京:南京大学出版社,2011.
[17]庄礼贤.流体力学[M].合肥:中国科学技术大学出版社,1991.
Air-spherical shells coupled vibration under compressible air
LIU Ping1,FU Gongyi2
(1.College of Civil Engineering & Architecture,Jiangsu University of Science and Technology,Zhenjiang 202003,China;2.School of Naval Architecture,Ocean & Civil Engineering,Shanghai Jiaotong University,Shanghai 200240,China)
Structures with large span are widely used in recent years,they are sensitive to wind load.How to consider air-space structures coupled vibration is a difficult problem.Here vibrations of three-dimensional spherical structures under incompressible /compressible air were analyzed with the assumption that on their boundary there was a simple harmonic vibration.Combined with a specific physical model,the theoretical solutions to two cases were derived,the theoretical results were discussed.It was shown that with incompressible air assumption,the surface pressures main components of structures are direct proportion to the vibration acceleration and the curvature radius of structures,the action force of air flow field on structures is equivalent to additional mass; for compressible air condition,the surface pressures of structures are direct proportion to vibration velocity and they are not related to the configuration of structures,the action force of air flow field on structures is equivalent to a viscous damping.Finally,numerical simulations were performed to verify the theoretical solutions.
compressible fluid; space structure; fluid-structure interaction
国家自然科学基金(51508238 )
2015-05-28修改稿收到日期:2015-09-06
刘平 男,博士,讲师,1983年4月生
TU311
A DOI:10.13465/j.cnki.jvs.2016.17.027

