岩土动力极限应变判据在边坡稳定分析中的应用

赖　杰，郑颖人，唐晓松，刘　云，谭仪忠

(1.火箭军工程大学 士官学院，山东 青州　262500；2.后勤工程学院 军事土木工程系，重庆　401311；3.重庆交通大学 土木工程学院，重庆　400074；4.中国人民解放军工程兵学院，江苏 徐州　221004)



岩土动力极限应变判据在边坡稳定分析中的应用

赖杰1,2，郑颖人2，唐晓松2，刘云3，谭仪忠4

(1.火箭军工程大学 士官学院，山东 青州262500；2.后勤工程学院 军事土木工程系，重庆401311；3.重庆交通大学 土木工程学院，重庆400074；4.中国人民解放军工程兵学院，江苏 徐州221004)

岩土材料受力从弹性进入塑性，最终发展到破坏，材料的屈服与破坏不同，屈服表示材料从弹性进入塑性状态，破坏表示从塑性发展到工程失稳。对于理想弹塑性材料，应力表述的判据难以区分屈服与破坏，为此提出采用极限应变作为岩土材料的破坏判据。给出了岩土材料动力极限应变的求解模型与方法，并以动力极限应变作为破坏准则，它既可以表述动力作用下材料的点破坏或开裂破坏，当点破坏贯通形成破坏面时，还可以表述材料整体破坏。通过地震作用下动力边坡工程算例，得到边坡滑体起裂的位置、演化过程和起裂极限荷载；当边坡中极限应变区贯通时得到边坡整体破坏极限荷载，并与数值极限分析中(超载法、强度折减法)采用位移不收敛破坏准则的计算结果比较，基本一致，验证了极限应变法在动力分析中的可行性。

屈服；破坏；极限应变；破坏判据；地震作用

自土力学学科形成之日起，岩土工程稳定性分析就采用极限分析法，并一直在工程上沿用至今，但这种方法也在不断的发展。对于边坡稳定问题，国际上许多学者提出了各种条分法，我国几十年前就提出了不平衡推力法，或称传递系数法[1-2]，陈祖煜等[3]提出了应用极限分析的上、下限解求解了边坡稳定问题，但传统极限分析法需要事先知道破坏面，限制了它的应用范围；ZIENKIEWICZ等[4-7]提出了有限元强度折减法与超载法，可以用先进的数值方法求解岩土结构的稳定系数与极限荷载，拓宽了极限分析应用范围；郑颖人等[8-10]根据有限元强度折减法与超载法的力学本质，将其统称为数值极限分析方法，归纳了三种破坏判据，扩展了其工程应用范围，并应用到地震作用下动力稳定分析。但上述这些方法都只能求解边坡的整体失稳，而不能获得边坡上任意点的点破坏，因而无法反映边坡的开裂与破坏过程。

固体材料随着受力的增大，一般都是先进入弹性状态，随后材料中某些部位材料屈服进入塑性状态，岩土材料是否从弹性进入塑性可依据屈服准则判定，但屈服不是破坏，屈服后可以继续承载，因而岩土工程设计中通常要求岩土进入塑性，以充分发挥岩土的自承作用。塑性充分发展后材料会进入破坏，材料是否发生破坏取决于是否满足破坏准则，但目前只有材料发生整体破坏时的准则，尚无材料发生点破坏的准则，文献[11]对静力问题提出了极限应变破坏判据，即材料中某点的应变达到或超出极限应变，该点材料就发生破坏，由此可判断材料的起裂位置，破坏演化过程与破坏面形态，以及材料出现开裂时的极限荷载；当破坏贯通整个岩土体时，岩土工程就发生整体破坏，由此可得到整体破坏时的极限荷载，这一极限荷载应与传统极限分析法得到的极限荷载基本一致。为研究边坡抗震问题，本文提出了一种求动力极限应变的方法，并将其应用到地震作用下边坡的动力稳定分析中。为验证计算的可靠性，对于整体破坏情况将极限应变判据和数值极限分析中(超载法、强度折减法)采用位移不收敛破坏判据进行了比较，计算结果吻合良好，证明了极限应变法在边坡动力稳定分析中的可行性。

1　极限应变与破坏的关系及其计算

图1为理想弹塑性材料的应力-应变曲线，当应力刚达到屈服应力σcu时，材料弹性剪应变γy达到极限，此刻材料不会发生破坏，但在屈服应力持续作用下应变不断增大，直至达到弹塑性极限剪应变γf时发生破坏。鉴于岩土工程一般为压剪破坏，所以岩土材料通常将此定义为材料的极限应变。材料中一个点的应变达到了极限应变，只代表该点发生破坏，在结构体持续受力时先破坏部分由于周围的制约作用还可以达到更大的应变，反映在材料上只出现局部开裂，不能代表材料整体破坏，因而对结构而言可称为局部开裂破坏。当材料中破坏点贯通整个结构时形成破坏面时，即破坏面上所有点都达到极限应变时，结构发生整体破坏[8,11]，这种情况称为整体破坏准则，这与当前的传统整体破坏准则计算方法不同但计算结果一致。

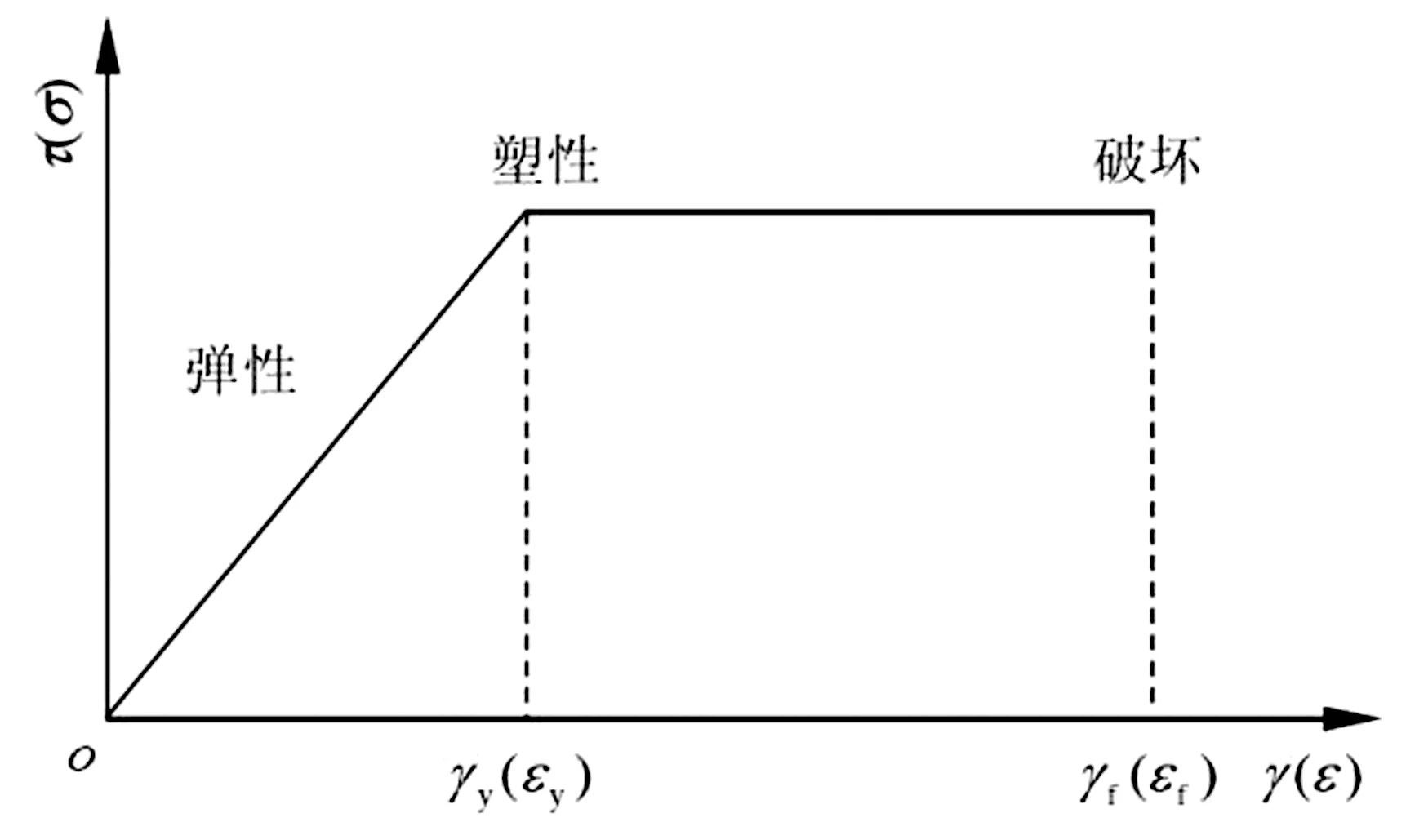
图1　理想弹塑性材料应力-应变关系Fig.1　Stress-strain relation for ideal lastic-plastic material

文献[11]中给出了弹性极限应变与弹塑性极限应变的数值求法，同时还给出了弹性极限应变的公式与弹塑性极限剪应变与弹塑性主应变的关系式。弹性极限主应变为：

(1)

(2)

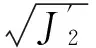
(3)

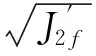
由于式(3)中的弹塑性极限主应变ε1f和ε3f还难以直接求得，但可通过数值模拟得到其数值大小，弹塑性极限主应变表示为：

(4)

式中:ε1f=χ1ε1y,ε2f=χ2ε2f，χ1、χ2为弹塑性极限总应变与极限弹性应变的比值，可由数值分析得到。

2　极限应变判据在边坡动力稳定分析中的应用

2.1边坡工程基本情况

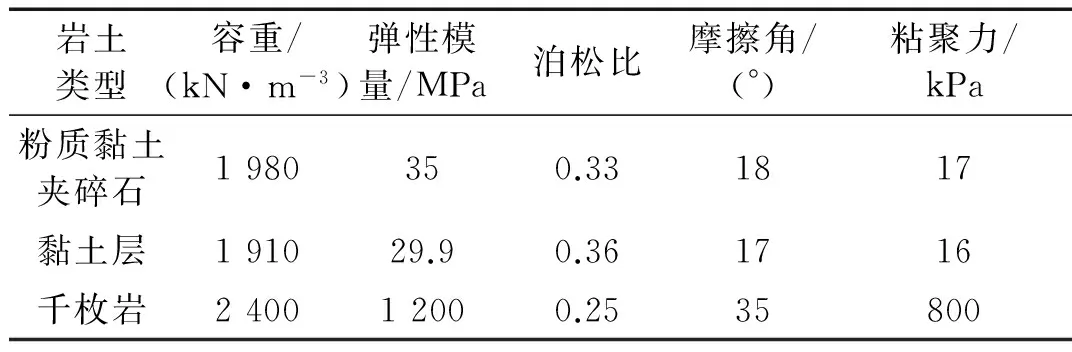
算例边坡工程位于略阳高速公路段，根据地勘报告，边坡主要由千枚岩、粉质黏土夹碎石、黏土层组成，滑坡所在地区为一斜坡，坡度25°～45°。因新修高速度公路要穿过山体，因此该路段为深挖路堑，滑坡前缘原设计开挖为三级边坡，单坡坡高10 m，坡率1∶0.75，在支护前滑体尚处于不稳定状态。滑坡体切坡后的外貌如图2所示，其物理力学参数见表1。

因该地连续暴雨，一、二级边坡开挖后长期裸露，引起坡体段近70 m范围产生了滑塌变形，表明原设计一排抗滑桩不足以稳定坡体，经过论证采用增加一排抗滑桩和预应力锚索的加强支护，支护结构的布设情况如图3所示，其中抗滑桩的桩身截面尺寸为2.4 m×1.8 m，原设计第一排桩长32 m，新增的第二排桩长23 m，预应力锚索的初始应力大小为640 kN，锚索强度为950 kN。

岩土类型容重/(kN·m-3)弹性模量/MPa泊松比摩擦角/(°)粘聚力/kPa粉质黏土夹碎石1980350.331817黏土层191029.90.361716千枚岩240012000.2535800

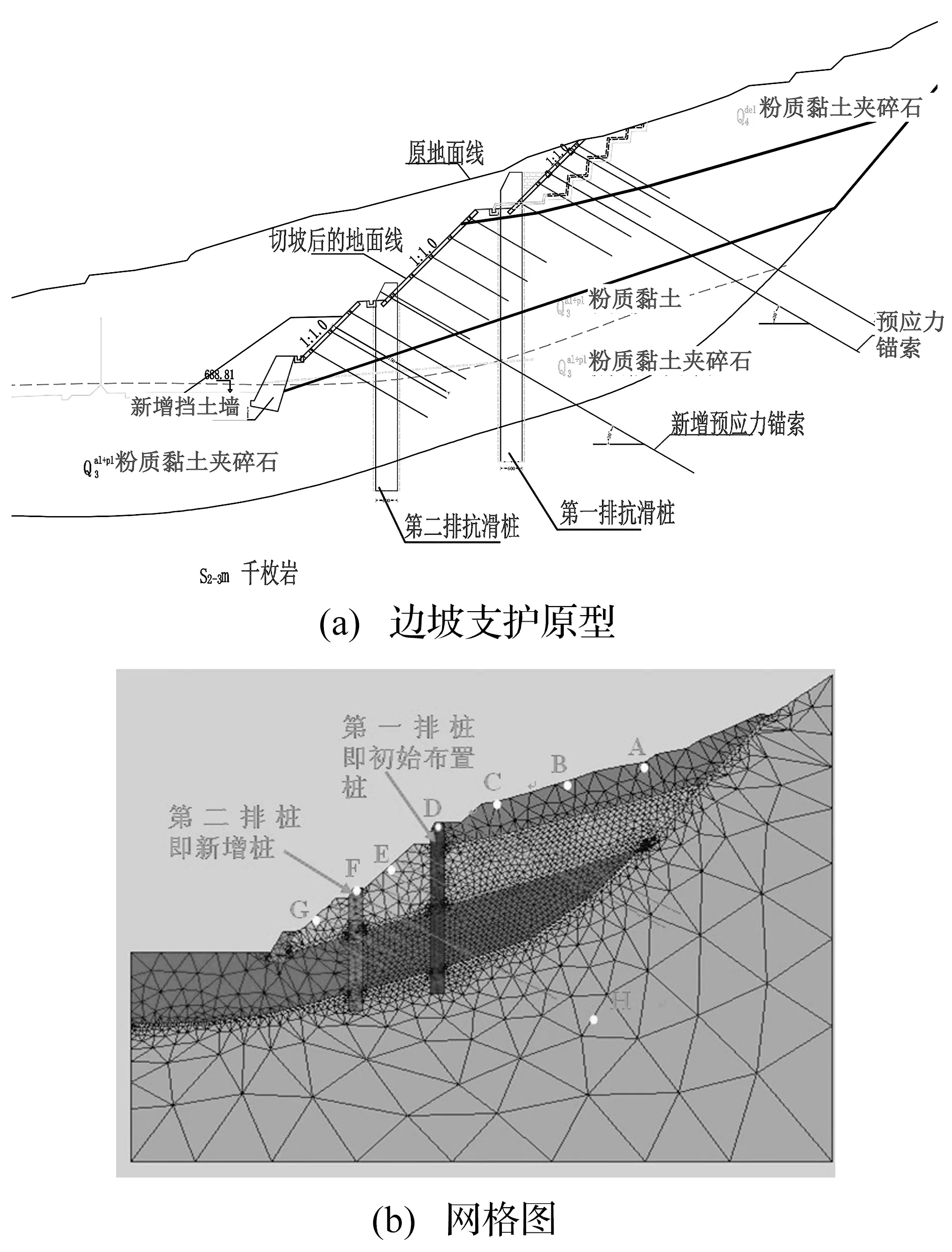
图3　边坡支护图Fig.3　Reinforced support program

2.2动力计算模型

2.2.1边界条件

在进行动力计算时，岩体材料为弹塑性材料，采用Mohr-Coulomb屈服准则，边界条件采用FLAC软件中的自由场边界(相当于无限域边界场)，从而达到模拟地震时无限场的条件。

2.2.2运动基本方程和瑞丽阻尼

边坡任意一点的运动微分方程可以写成:

Mu″+Cu′+Ku=-MIu″g

(5)

式中：M为质量刚度，C为阻尼矩阵，K为刚度矩阵，u″、u′、u为t时刻质点的加速度、速度及位移，u″g为地震加速度。

C=aM+βK

(6)

式中：a、β均为阻尼系数，则任意阶阻尼比λn等于下式：

(7)

一般常假定λi=λj=λ，此时a=2λw1w2/(w1+w2)及β=2λ/(w1+w2)，阻尼比与圆频率关系如图4所示。

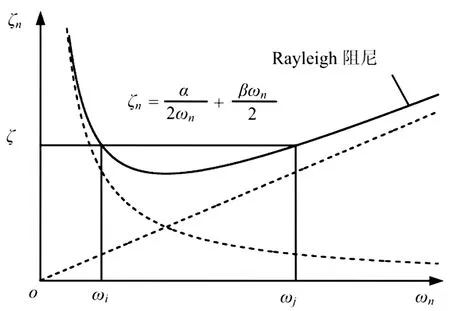
图4　阻尼比与圆频率关系图示Fig.4　Relationship between damping ratio relation and circular frequency

采用阵型阻尼比5%，结构频率选取0.2～10 Hz进行考虑，得到α=0.019 6，β=0.009 8

2.2.3输入地震波

从底部输入的地震波为Qiqi波(Qiqi，1997年，NS向)，峰值加速度为0.2 g(8度基本烈度[11])，通过人为截取地震的主能量段，输入地震波持时10 s，过滤波及基线校正后的地震波见图5。

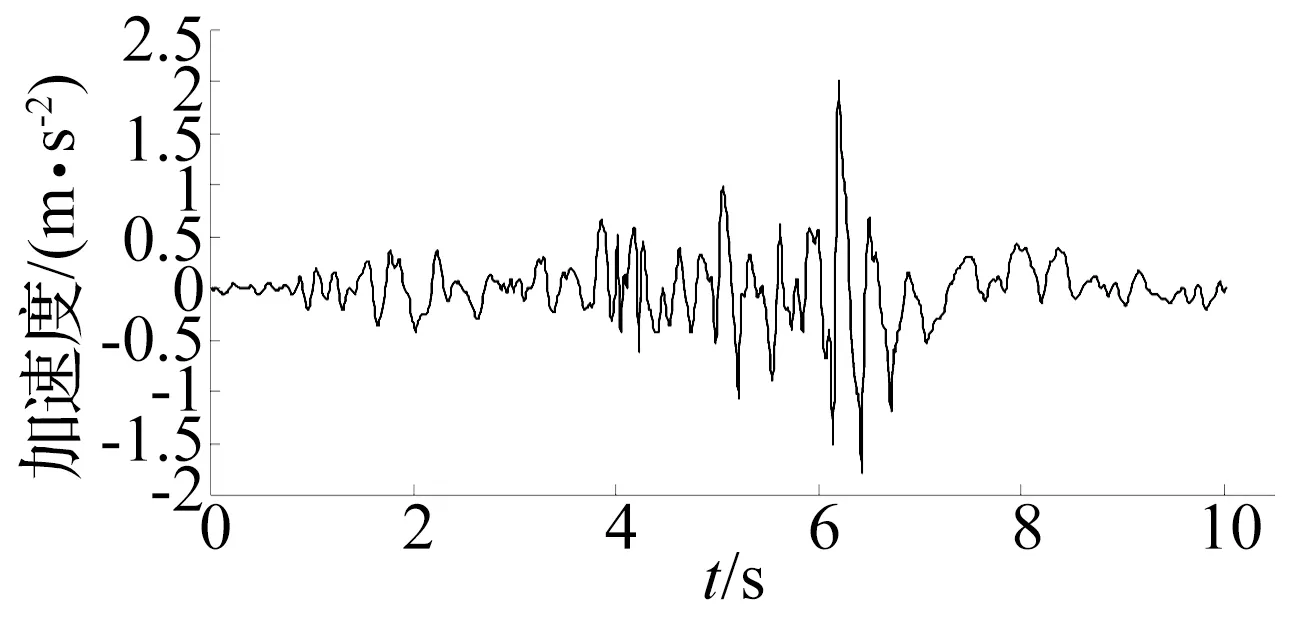
图5　输入的地震波Fig.5　Input seismic wave

2.3滑体动力极限应变的确定

为得到滑体(粉质黏土夹碎石和黏土层)的极限剪应变，建立一正方体试块模型，并输入土体的力学参数(见表1)。对于静力问题，正方体试块为边长0.15 m的立方体，但对动力问题中需考虑波的边界反射影响，即入射波和反射波相互叠加使得单元存在一定的加速度放大效应，单元承受荷载大于输入的荷载。为降低波边界反射的影响，将试块模型适当放大，设置为1.5 m的立方体，且将单元真实承受的荷载定为输入荷载乘以单元的动力放大系数(加速度放大效应影响)。试块底部固定，顶部施加地震波，地震波为剪切波，传播方向为垂直向。采用有限元超载法，通过不断增加地震波的峰值，直到试块失稳破坏。模型内共设置1～12个监测点，具体位置如图6(a)所示。计算结束后，从图6(b)和图7可以看出，此时碎石土极限应变计算中监测点11单元的应变最大，且只有该单元发生破坏，而其余单元均未达到破坏。正是由于该单元破坏，最终导致模型整体破坏，因而可认为该单元的平均应变值为该材料的极限应变。图7示出了表层碎石土材料监测点11单元地震峰值荷载与应变的关系曲线，单元破坏时应变突变，由此得到粉质黏土夹碎石的极限剪应变为3.11%(为破坏单元的剪切应变平均值)；同理，得到下部黏土层的极限剪应变为3.14%。

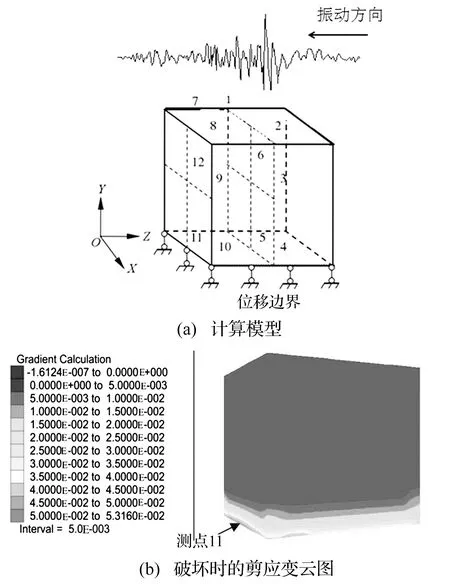
图6　单元计算模型Fig.6　Calculated model

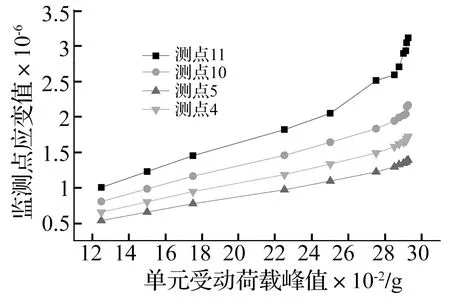
图7　监测点荷载-应变关系曲线Fig.7　Load-stain relationship curve for key points

2.4动力稳定性分析

当前的数值极限分析中在地震动力稳定分析时通常采用超载法和强度折减法，前者通过不断增加荷载使材料达到破坏，后者通过不断折减岩土体的抗剪强度参数使材料达到破坏状态。它们的破坏判据主要使用数学上的突变理论[8]，如位移非线性计算中从收敛到不收敛即认为材料破坏，但其物理意义并不明确。当材料刚达到破坏状态时的应变称为极限应变，极限应变失稳判据使得物理意义更加明确，且位移不收敛判据(在超载法和强度折减法中使用)无法反映边坡的开裂与破坏过程，也得不到材料初始开裂时的极限荷载，然而极限应变法可以做到。极限应变法判据和位移不收敛判据都可以求得材料整体破坏时的极限荷载，为比较不同方法计算结果的差异，应用上述判据求解本算例边坡的极限荷载，并进行比较。

(1)极限应变判据

由2.3节得到了粉质黏土夹碎石和黏土层的极限应变分别为3.11%和3.14%，当土层应变大于其极限应变时，土体发生开裂破坏。图8中对粉质黏土夹碎石土层列出大于3.11%的应变，对黏土层列出大于3.14%的剪切应变云图，根据该应变可以得到滑体在地震作用下从稳定到破坏的发展演化过程。由图可见，当地震波峰值为0.238 g时，坡顶滑面处出现开裂，见图8(a)，由此得到边坡起裂的极限荷载为0.238 g；随着地震作用的增大，破裂面向下发展，当地震波峰值为0.30 g时，逐渐形成两个潜在滑面，其中第二排桩后下层黏土层潜在滑面的应变都大于该层土极限应变3.14%，见图8(b)(虚线部分)，表明第二排桩后的滑面已经全部开裂，但由于受到抗滑桩的阻挡，没有形成整体破裂面，同时上层粉质黏土夹碎石潜在滑面应变大于该层极限应变3.11%的区域尚未贯通，因而不会发生整体破坏；但当地震波峰值达到0.336 g时，见图8(c)，上层滑面从桩后“越顶”剪出，此时大于该土层大于极限剪应变3.11%剪切区完全贯通，达到了整体破坏，因此对应的整体破坏极限荷载为0.336 g。

(注：对粉质黏土夹碎石土只列出大于3.11%的应变，对黏土层只列出大于3.14%应变)图8　输入不同地震波峰值的剪切应变云图Fig.8　Shear-strain nephogram under different earthquakes

(2)超载法(位移不收敛判据)

根据超载法，利用位移收敛性准则判断边坡整体是否失稳[8,11-12]，从而得到极限荷载。从监测点的水平位移时程曲线上看(见图9)，当输入的地震波峰值为0.33 g时，监测点在第4 s时刻位移增长很快，地震结束后位移收敛，此时边坡是稳定的；当地震波峰值为0.34 g时，监测点也在4 s时刻位移增加迅速，地震结束后位移不收敛，按收敛性判据表明滑体已失稳破坏。

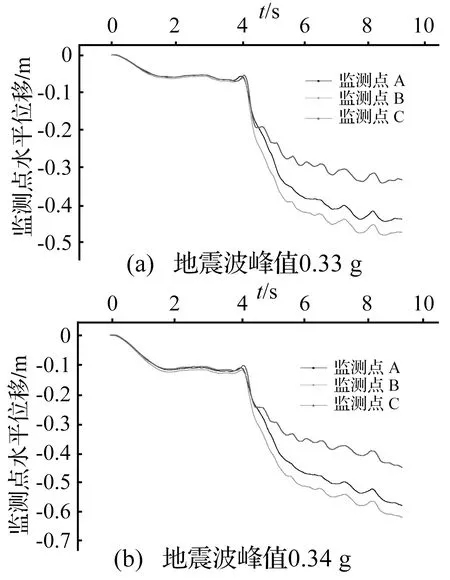
图9　监测点位移时程曲线Fig.9　Time history curves of displacement for key points

(3)强度折减法(位移不收敛判据)

图10　折减系数与监测点位移关系曲线Fig.10 Reduction factor-displacement curve

利用强度折减法[9,13]，采用位移不收敛失稳判据，通过不断降低土层的抗剪强度参数使边坡达到极限状态，从而得到极限荷载[14]。从图10可以看出，当折减系数为1.04时，监测点在地震结束后的位移不再增大，此时边坡是稳定的，当折减系数为1.05时，监测点震后水平位移不断增大，已不再收敛，表明此时滑体已经破坏，边坡的动力安全系数为1.04。

2.5极限荷载的比较

表2列出了不同判据的极限荷载及其比较，由表可知：采用位移不收敛判据的强度折减法得到的极限荷载与极限应变判据得到的极限荷载相差为7.14%；采用位移不收敛判据的超载法与极限应变判据得到的极限荷载相差为1.78%，数据比较接近，验证了极限荷载法的合理性。

表2　几种判据极限荷载比较

2.6桩身前后动土压力分析

图11为数值计算出来的在抗震设防烈度0.2 g时第一排桩的桩身动土压力分布情况，桩后土压力为桩的推力，桩前土压力为抗力。可以看出桩身两侧的动土压力的大小与地震时刻密切相关，初始时刻应力较小，地震峰值时刻(第6 s)应力增长明显。桩后动土压力明显较大，且主要位于滑面以上，在距桩顶13.8 m位置处桩后动土压力最大(见图11(a))，这符合一般桩后推力分布规律。桩前抗力动土压力较小，且随桩长压力逐渐增大，滑面以下部分抗力较大，这是由于前面已经有了第二排桩的支挡作用，保证了桩的稳定。

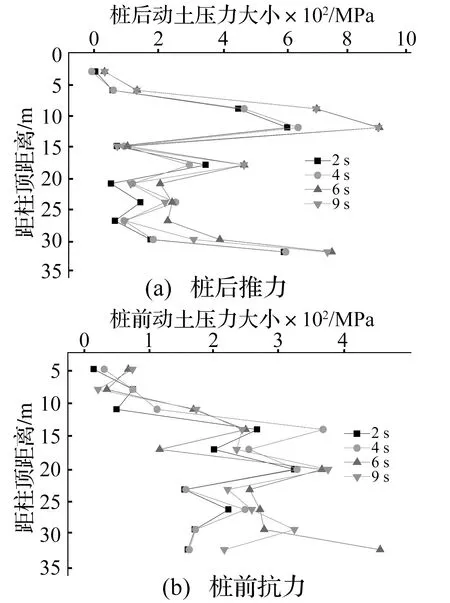
图11　桩身动土压力分布(0.2 g)Fig.11 Dynamic soil pressure of pile(0.2 g)

3　结　论

(1)材料的屈服与破坏不同，屈服表示材料从弹性进入塑性状态，破坏表示从塑性发展到工程失稳。对于理想弹塑性材料，应力表述的判据难以区分屈服与破坏，为此提出采用极限应变作为岩土材料的破坏判据。

(2)初步尝试提出了岩土材料的动力极限应变的求解模型与方法，并以此作为动力破坏准则，它既可以表述动力作用下材料的点破坏或开裂破坏，当点破坏贯通形成破坏面时，还可以表述材料整体破坏。对于整体破坏情况，它与当前数值极限分析的破坏判据不同，但计算结果相同。

(3)通过地震作用下动力边坡算例，得到边坡滑体初始开裂的位置和演化过程，以及初始开裂的极限荷载；当边坡中极限应变区贯通时得到边坡的极限荷载，并与采用位移不收敛失稳判据的数值极限分析(超载法、强度折减法)比较，结果基本一致，验证了极限应变法的可行性。

[1]郑颖人，陈祖煜，王恭先，等.边坡与滑坡工程治理[M].北京：人民交通出版社，2010.

[2]钱家欢,殷宗泽.土工原理与计算[M].第2版.北京:中国水利水电出版社,2000.

[3]陈祖煜.土力学经典问题的极限分析上、下限解[J].岩土工程学报，2002,24(1):1-11.

CHEN Zuyu.Limit analysis for the classic problems of soil mechanics[J].Chinese Journal of Geotechnical Engineering,2002,24(1):1-11.

[4]ZIENKIEWICZ O C,HUMPHESON C,LEWIS R W.Associated and non-associated viscoplasticity and plasticity in soil mechanical[J].Geotechnique,1975,25(4):671-689.

[5]ZIENKIEWICZ O C.The birth of the finite element method and of computational mechanics[J].International Journal for Numerical Methods in Engineering,2004,60(1):3-10.

[6]郑宏,李春光,李焯芬,等.求解安全系数的有限元法[J].岩土工程学报,2002,24(5):626-628.

ZHENG Hong,LI Chunguang,Lee C F,et al.Finite element method for solving the factor of safety[J].Chinese Journal of Geotechnical Engineering,2002,24(5):626-628.

[7]LIU S Y,SHAO L T,LI H J.Slope stability analysis using the limit equilibrium method and two finite element methods[J].Computers and Geotechnics,2015,63:291-298.

[8]郑颖人.岩土数值极限分析方法的发展与应用[J].岩石力学与工程学报,2012,31(7):1297-1316.

ZHENG Yingren.Development and application of numerical limit analysis for geological materials[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(7):1297-1316.

[9]郑颖人，叶海林，黄润秋.地震边坡破坏机制及其破裂面的分析探讨[J].岩石力学与工程学报,2009,28(8):1714-1723.

ZHENG Yingren，YE Hailin，HUANG Runqiu.Analysis and discussion of failure mechanism and fracture surface of slope under earthquake[J].Chinese Journal of Rock Mechanics and Engineering,2009,28(8):1714-1723.

[10]郑颖人，叶海林，黄润秋，等.边坡地震稳定性分析探讨[J].地震工程与工程振动,2010,30(2):173-180.

ZHENG Yingren,YE Hailin,HUANG Runqiu,et al.Study on the seismic stability analysis of a slope[J].Journal of Earthquake Engineering and Engineering Vibration,2010,30(2):173-180.

[11]阿比尔的,冯夏庭,郑颖人,等.岩土类材料应变分析与基于极限应变判据的极限分析[J].岩石力学与工程学报,2015,34(8):1552-1560.

ABI Erdi,FENG Xiating,ZHENG Yingren,et al.Strain analysis and numerical analysis based on limit strain for geomaterials[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(8):1552-1560.

[12]李海波,肖克强,刘亚群.地震荷载作用下顺层岩质边坡安全系数分析[J].岩石力学与工程学报,2007,26(12):2385-2394.

LI Haibo,XIAO Keqiang,LIU Yaqun.Factor of safety analysisof bedding rock slope under seismic load [J].Chinese Journal of Rock Mechanics and Engineering,2007,26(12):2385-2394.

[13]郭院成,陈涛,钱辉.基于强度折减的边坡动力安全系数确定方法研究[J].土木工程学报,2012,45(增刊2):117-120.

GUO Yuancheng,CHEN Tao,QIAN Hui.The determination method of dynamic safety factor for slope based on strength reduction[J].China Civil Engineering Journal,2012,45(Sup2):117-120.

[14]DONG Tianwen,ZHENG Yingren.Limit analysis of vertical anti-pulling screw pile group under inclined loading on 3D elastic-plastic finite element strength reduction method[J].Journal of Central South University,2014,21:1165-1175.

Application of rock and soil’s dynamic limit strain criterion in stability analysis of slope engineering

LAI Jie1,2,ZHENG Yingren2,TANG Xiaosong2,LIU Yun3,TAN Yizhong4

(1.Sergeant College,The Rocket Force Engineering University,Qingzhou,Shandong 262500,China; 2.Department of Civil Engineering,Logistical Engineering University,Chongqing 401311,China; 3.School of Civil Engineering,Chongqing Jiaotong University,Chongqing 400074,China; 4.Academy of People’s Liberation Army,Xuzhou,Jiangsu 221004,China)

When bearing external load,geotechnical material turns from elastic state to plastic state,eventually to destruction state.Material’s yield state is different from its failure state.The yield state means that a material has developed from elastic state into plastic state.However,the failure state,means that a material has developed from plastic state into unstable state.For ideal elastic-plastic materials,stress criterion is difficult to distinguish between yield and failure.Here,the limit strain was proposed as a damage criterion for geotechnical materials.The solving model and method for the dynamic limit strain of geotechnical materials were put forward,and the dynamic limit strain was taken as a failure criterion.It could be used to express integral damage or local failure of materials under dynamic action.When point damages connect together to from a failure surface,the overall destruction could be described.Based on a slope project under earthquake action,the position of initial crack,the evolutionary process of the crack at the slope and the limit crack load were obtained.The limit load calculated with the limit strain criterion was in accordance with the results computed using the numerical limit analysis with the displacement unconverged criterion (the overload method and the strength reduction method),the feasibility of the limit strain criterion in the dynamic analysis was verified.

yield; failure; limit strain; failure criterion; earthquake action

国家重点研究发展计划(973)项目(2011CB013600)；国家自然科学基金(51378496;51178457)；重庆自然科学基金(CSTC2013jcyjys0002)

2015-11-20修改稿收到日期：2016-02-12

赖杰 男，博士生，1986年生

郑颖人 男，中国工程院院士，博士生导师，1933年生

P642.2

A DOI:10.13465/j.cnki.jvs.2016.17.003