基于EKF-BP网络的矿用自卸车轮胎材料参数辨识

张菲菲，谷正气,2，张　沙，马骁骙，朱一帆

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙　410082;2.湖南文理学院，湖南 常德　415000)



基于EKF-BP网络的矿用自卸车轮胎材料参数辨识

张菲菲1，谷正气1,2，张沙1，马骁骙1，朱一帆1

(1.湖南大学 汽车车身先进设计制造国家重点实验室，长沙410082;2.湖南文理学院，湖南 常德415000)

轮胎材料参数对轮胎有限元模型至关重要，但轮胎材料多，结构复杂，导致轮胎材料参数难以获取，对此提出利用扩展卡尔曼(EKF)优化的BP神经网络辨识轮胎材料参数的方法。基于轮胎有限元模型，模拟了轮胎脉冲工况动态仿真，将仿真得到的轮胎垂向加速度作为网络理想输入样本，将需要辨识的轮胎材料参数作为网络理想输出样本，通过网络训练，建立两者之间的非线性映射网络模型。将经过小波去噪的轮胎垂向加速度试验数据输入训练好的网络，有效辨识出了轮胎材料参数。通过材料参数辨识的轮胎模型在相应工况下的仿真数据与试验数据的对比，显示两者最大误差为6.45%，证明了基于材料参数辨识的轮胎有限元模型垂向特性的准确性。

矿用自卸车轮胎；参数辨识；BP神经网络；扩展卡尔曼；小波去噪

目前，汽车轮胎模型分为物理模型、经验-半经验模型和有限元模型[1]。其中，物理模型并不能完全模拟轮胎结构，精度较差；经验-半经验模型的建立依赖于丰富的研究经验和大量的试验数据，而矿用自卸车轮胎体型巨大，台架投资成本高，暂无相应试验条件。因此本文拟通过有限元法建立自卸车轮胎模型。由于矿用自卸车轮胎价格昂贵，通过试验获取压制后的各层材料参数成本极高，借助神经网络结合整车行驶脉冲试验可间接辨识出轮胎各层材料参数。

在各类神经网络模型中，应用较为广泛的是前馈神经网络模型，较常用的算法是BP算法，但在实际运用中，BP神经网络自身存在一些不足，如收敛速度慢，易陷入局部极小值，泛化能力不能保证等[2]。近年来，国内外学者对此进行了大量研究，YAM等[3]提出了使用Cauchy不等式和线性代数方法得到最优初始权值，能有效的加快收敛速度。谢延敏等[4]采用遗传算法优化BP神经网络权值，极大地提高网络预测精度。PICHLER等[5]通过试验数据训练一个具有两个隐层的BP神经网络，辨识得到车辆质心侧偏角。GUARNERI等[6]利用神经网络预测不同工况下轮胎径向力与垂向力。于德介等[7]提出了一种基于神经网络的结构参数识别方法，采用GSL变换对训练样本数据进行预处理，提高了参数识别精度。上述改进方法中，有些只针对单一缺点进行改进，有些并没有改变网络的训练算法。借助扩展卡尔曼算法优化BP神经网络即将扩展卡尔曼算法替代神经网络的BP算法，不仅可以提高网络学习效率，且能避免网络陷入局部极小值[8]。

本文利用EKF-BP网络对轮胎材料参数进行辨识，通过预测输出与期望输出的对比，验证了该方法对轮胎材料参数的辨识能力，并借助db13小波对矿用自卸车脉冲试验数据进行去噪处理，将经过去噪的轮胎垂向加速度试验数据带入训练好的网络模型，有效辨识出了轮胎材料参数。通过不同车速、载荷下轮胎模型仿真数据与试验数据对比，结果表明基于材料参数辨识的轮胎有限元模型与实际轮胎的垂向特性相接近。

1　有限元模型建立

1.1轮胎几何模型

根据厂商提供的数据，采用CAD绘制轮胎截面图。由于轮胎模型结构复杂，为了保证能够顺利划分网格，对轮胎模型进行了一定的简化，如省略轮胎花纹[9]；采用刚体单元模拟轮辋[10]等；将本轮胎模型简化为四个组成部分，即钢丝圈，帘布层，带束层，橡胶层，最终轮胎截面轮廓及结构分布如图1所示，轮胎宽1 111 mm，轮胎直径3 566 mm。

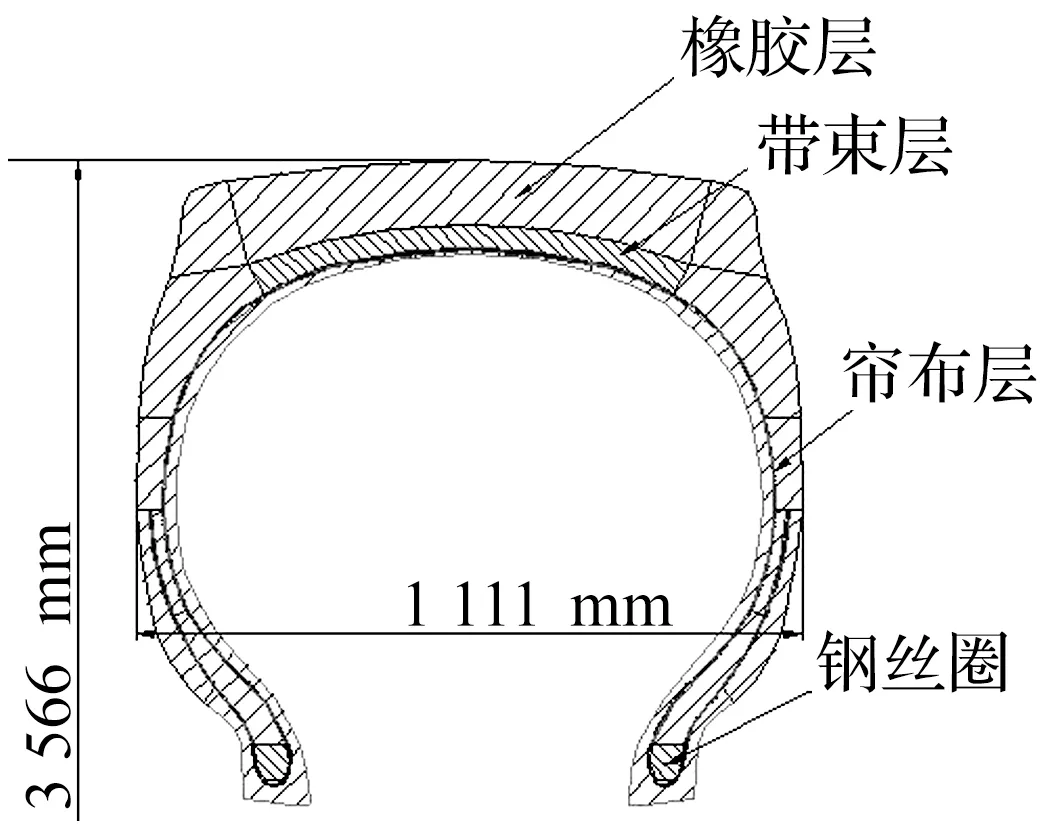
图1　轮胎截面轮廓及结构分布Fig.1　Cross-section contour and structure distribution of tire

1.2轮胎-脉冲路面有限元模型

将轮胎截面轮廓图导入HyperMesh中进行网格划分，划分网格时注意网格大小均匀，避免产生角度过大的网格，轮胎截面二维网格如图2所示。

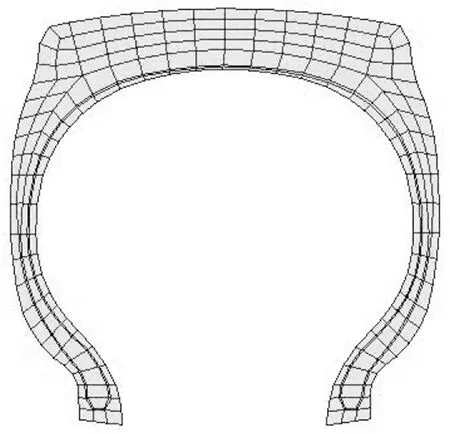
图2　轮胎截面二维网格Fig.2　2D mesh of tire cross-section

将二维网格绕着轮胎中心轴旋转360°，得到轮胎三维有限元模型。考虑到仿真中无法精确模拟真实矿山路面，为排除矿山路面不确定的影响，本文选取脉冲工况进行仿真，其中，根据国标GB/T 4970—2009中的规定，将脉冲块设置为高140 mm，底边宽200 mm的三角形单凸块，并将轮胎与脉冲块接触区域的网格细化，如图3所示。最终该模型共有25 236个单元，28 213个节点。

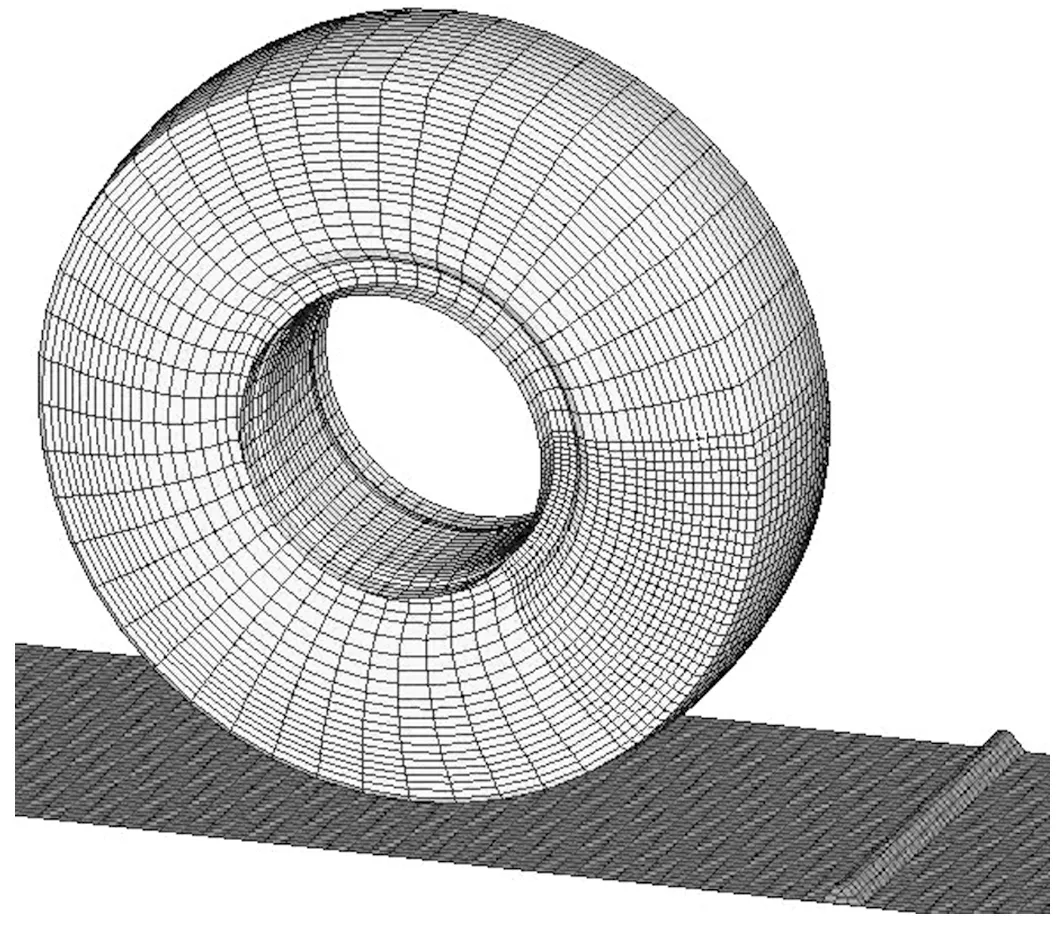
图3　轮胎-脉冲路面仿真有限元模型Fig.3　Finite element model of tire-pulse pavement

2　采用EKF优化BP神经网络研究

采用EKF优化BP神经网络即将前馈神经网络的权值、阈值作为扩展卡尔曼算法的状态，网络输出作为算法的观测。由于EKF-BP解的递推性，每一步的状态更新只需得到前一步的估计值和新的输入样本，所以训练过程中只需储存前一步的估计值，因而极大地提高了算法学习效率和计算速度；由于在训练过程中，除了更新网络的权值阈值外，对携带二阶微分信息的逼近误差方差矩阵同样进行更新，因而具有全局最优性，解决了BP神经网络易陷入局部极小值的问题[11]。

应用扩展卡尔曼优化BP神经网络的训练问题 可以描述为：用目前所获得的所有观测数据去寻找状态(权值、阈值)W的最小方差估计。对于该网络的训练问题，给出如下递推形式的EKF-BP解[12]：

(1)

(2)

(3)

(4)

(5)

以上5个公式即扩展卡尔曼优化BP神经网络的基本递推公式，其中，随机观测噪声vk为典型的零均值白噪声，微分矩阵Hk为：

(6)

该EKF-BP网络训练步骤如下：

1)为逼近误差方差矩阵Pk，噪声方程矩阵Qk，观测噪声方差矩阵Rk赋初值；

3)应用式(4)、(5)更新逼近误差方差矩阵Pk和EKF增益矩阵Kk；

4)应用式(3)更新状态向量；

5)重复步骤2)～4)，直到误差达到给定的精度要求，训练结束。

3　EKF-BP网络辨识能力分析

3.1辨识样本获取

本轮胎有限元模型由钢丝圈、帘布层、带束层及橡胶层四部分组成，每个部分赋予不同的材料属性，包括弹性模量、泊松比、密度等参数，其中弹性模量和泊松比是两个重要但不易得到的参数，本文选取这两种参数进行辨识。通过查阅资料[13-15]，确定本轮胎模型材料参数辨识范围如表1所示。采用优化拉丁超立方抽样方法[16]获得40组材料参数，通过轮胎有限元空载、30 km/h、脉冲工况动态仿真，得到相对应的轮胎垂向加速度曲线。这样就得到40组样本，从中随机选取35组用于训练，剩余5组用于测试。

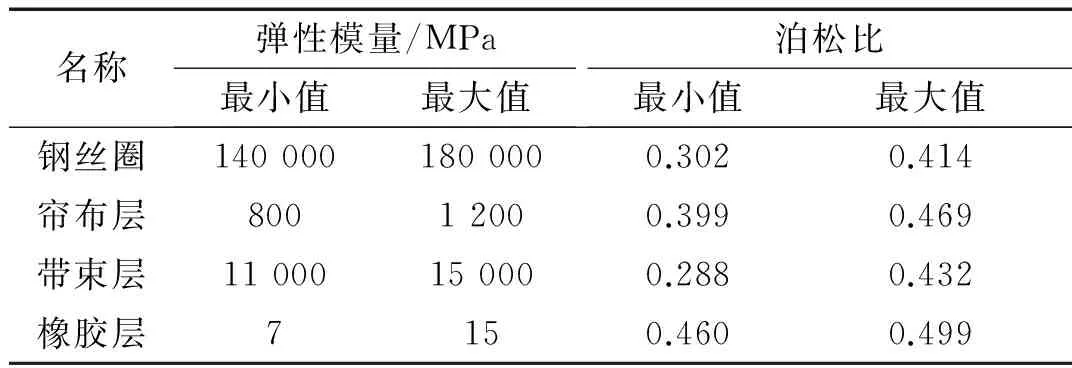
表1　各层材料参数辨识范围

3.2网络训练

本文取35组矿用自卸车左前轮垂向加速度作为理想网络输入样本，对应的轮胎材料参数为理想网络输出样本，基于EKF-BP网络的递推公式，建立EKF优化的BP神经网络，其中BP神经网络隐含层包含10个神经元，传递函数为双曲正切S型(tansig)，输出层为线性传递函数(purelin)，扩展卡尔曼算法参数初始化P=40I，Q=40I，R=40I，I为适当维的单位矩阵，最小允许误差设为0.001。对该网络进行训练，建立了轮胎材料参数与轮胎垂向加速度之间的非线性映射关系。

3.3辨识能力分析

将5组测试样本的垂向加速度带入训练好的EKF-BP网络进行计算，可得到对轮胎材料参数的预测输出。表2为期望输出(即5组测试样本的材料参数)、分别利用BP神经网络和EKF-BP网络得到的预测输出及训练结束所需迭代次数，从表中可看出EKF-BP网络比BP神经网络收敛速度快，迭代次数少。图4为利用BP网络和EKF-BP网络对四种组成部分弹性模量及泊松比进行预测的相对误差，从图中可以明显看出，BP网络预测误差均在±6%以内，平均预测误差为2.61%，EKF-BP网络预测误差均在±2%以内，平均预测误差为0.51%，与标准BP网络相比，EKF-BP网络预测精度高，更加接近期望值，验证了EKF-BP网络对轮胎材料参数具有较好的辨识能力。

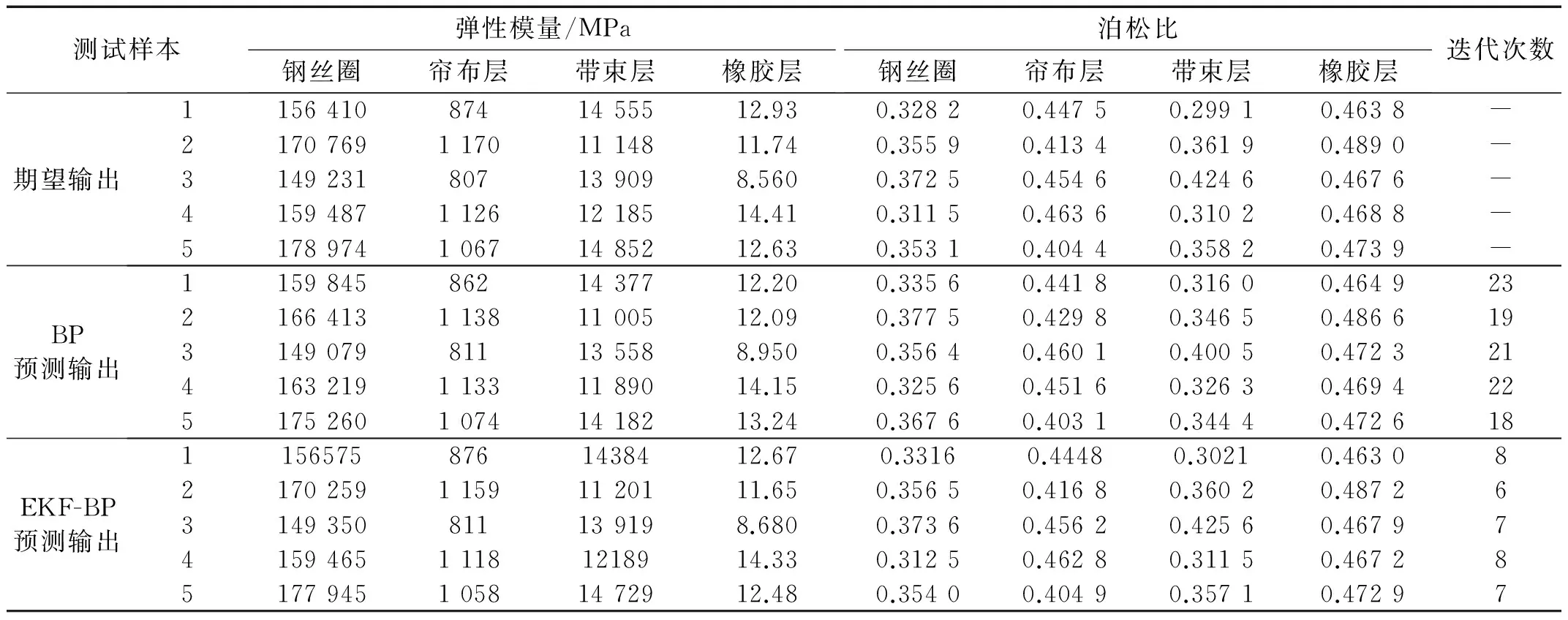
表2　期望输出与BP/EKF-BP网络预测输出

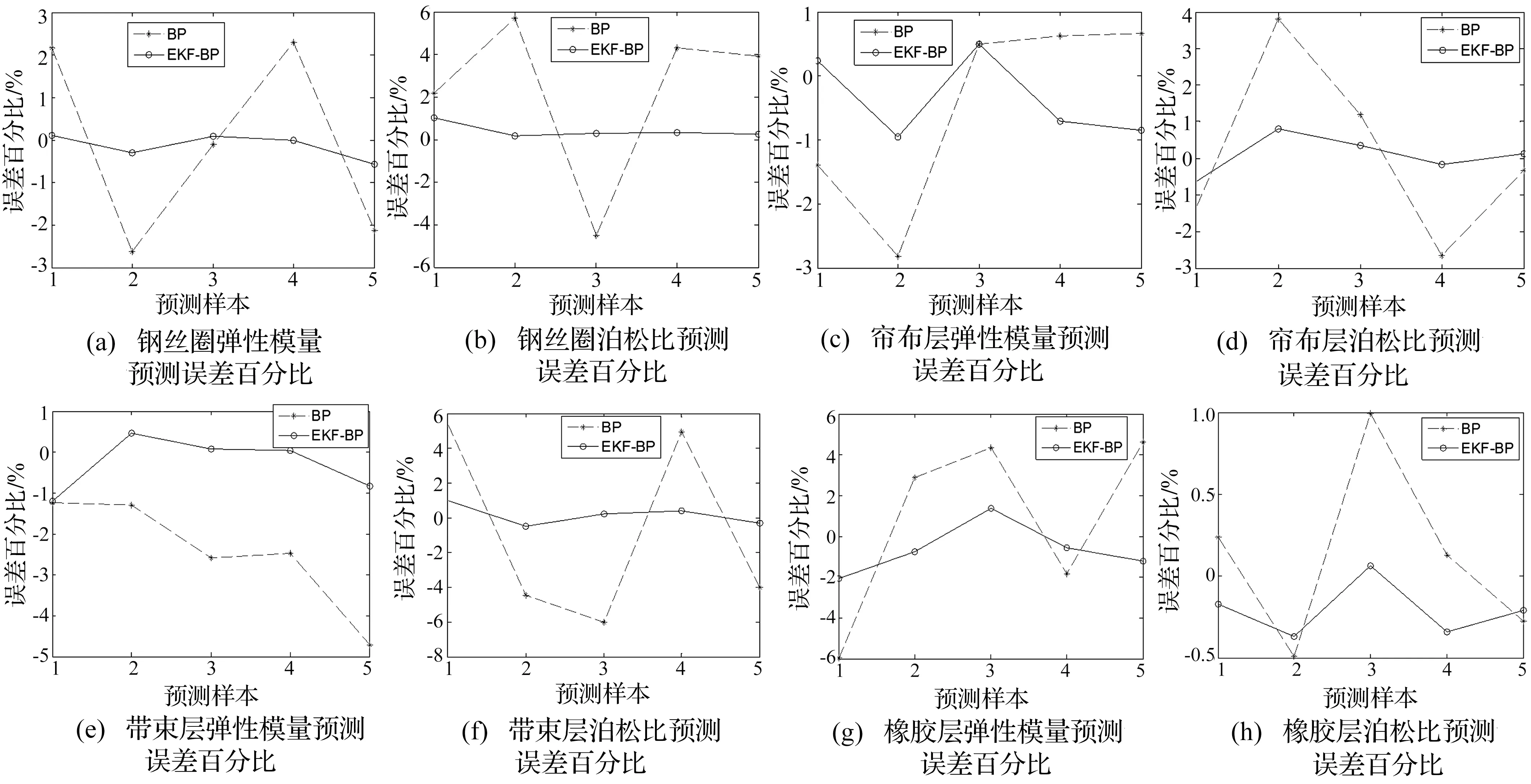
图4　预测误差百分比Fig.4　Percentage of prediction error

4　参数辨识及试验验证

4.1脉冲试验

为了辨识出轮胎材料参数，设计了自卸车脉冲工况行驶试验。其中脉冲块高140 mm，底边宽200 mm，为避免脉冲块变形，选取脉冲块制作材料为钢材，试验工况分为空载和满载两种工况，试验轮胎充气压力为0.7 MPa，试验车速分别为10 km/h,20 km/h,30 km/h，试验数据采样频率为512 Hz，采样时间为22 s，如图5所示。

图5　整车脉冲工况试验Fig.5　Pulse condition test of the vehicle

考虑到采样数据太多，且研究对象为车轮过脉冲块时的数据，所以只取包含脉冲数据的时间段进行分析。根据试验记录，当车速为30 km/h、空载工况时，汽车前轮在19.36 s开始通过脉冲块，试验得到的左前轮垂直加速度曲线及功率谱密度曲线如图6(a)所示，为更好观察低频成分，将功率谱密度曲线中0～80 Hz的频率范围放大显示，如图6(b)所示。

分析本试验数据可知，轮胎垂向加速度时间历程数据杂乱，且其功率谱密度中的高频成分很明显。这是由试验数据中的噪声引起的，所以有必要对试验数据进行去噪处理，得到合理有效的试验数据。

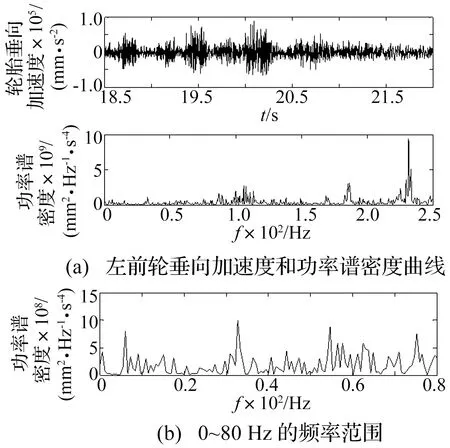
图6　左前轮垂向加速度和功率谱密度曲线Fig.6　Vertical acceleration and power spectrum density curve of left front wheel

4.2小波去噪

Daubechies小波是由著名的小波分析学者Daubechies构造的小波函数，一般简写成dbN，N是小波的阶数，计算结果表明，N越小能量越集中在低频段。但N太小会导致尺度函数的光滑性差，逼近效果较差[17]。在工程应用中，有效信号一般表现为低频信号，噪声表现为高频信号，所选小波函数应尽可能地使信号能量集中在低频区。结合本试验数据的特点，文献[18-19]的分析，本文选用db13小波对试验数据进行去噪分析，去掉高频噪声的同时，保留信号的原有特征。

本文使用matlab中的小波工具箱对信号进行小波分析，选用db13小波，分解层数为5层，采取软阈值去噪。最终去噪后的左前轮加速度曲线及其功率谱密度曲线如图7所示。

图7　去噪信号及其功率谱密度曲线Fig.7　Curves of denoised signal and its power spectrum density

对比分析图6，7可知，从时域上，去噪波形较为平滑，很好的保留了信号的突变部分；从频域上，不仅将30 Hz以上的高频几乎全部滤除，且较好的保留了所需的低频信号。所以采用db13小波对左前轮垂向加速度信号进行去噪，取得了良好的效果。

4.3参数辨识及结果验证

将图7中前轮过脉冲块引起的振动加速度，即19.36～19.70 s时间段的数据，作为输入样本代入已训练好的EKF-BP网络中，辨识出轮胎材料参数如表3所示。将该辨识参数作为轮胎有限元模型的输入，进行30 km/h空载脉冲路面的仿真，得到轮胎垂向加速度及其功率谱密度如图8所示，图9为30 km/h空载工况试验得到的前轮过脉冲块时的左前轮垂向加速度及其功率谱密度曲线。

表3　轮胎材料参数辨识结果

由图8可以看出轮胎仿真垂向加速度在-0.6×104～1×104mm/s2内波动，与图9所示轮胎试验垂向加速度波动范围一致。图8中仿真模型功率谱密度主要集中在低频段，其中峰值频率约为6.11Hz，而图9中轮胎试验功率谱密度也集中在低频段且峰值频率为5.86 Hz，仿真模型结果和试验结果比较吻合。

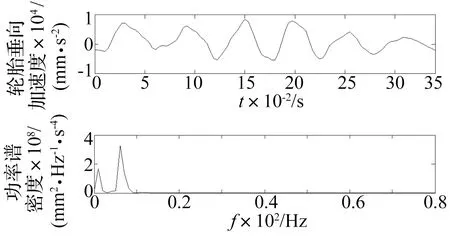
图8　轮胎垂向加速度及其功率谱密度仿真曲线Fig.8　The simulation curves of tire vertical acceleration and its power spectrum density

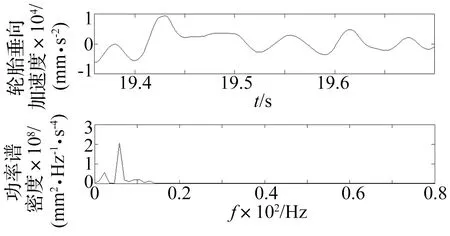
图9　轮胎垂向加速度和功率谱密度试验曲线Fig.9　The test curves of tire vertical acceleration and its power spectrum density

将表3中辨识得到的材料参数作为轮胎有限元模型的输入进行不同车速、载荷下的仿真，将得到的轮胎中心点垂向加速度时域最大值及峰值频率与同工况下去噪试验数据相对比，结果如表4所示。从表中可明显看出，不同车速、载荷下，基于材料参数辨识的轮胎模型仿真的最大加速度及峰值频率均与试验相接近，其中最大加速度的最大误差百分比为6.45%，峰值频率的最大误差百分比为6.15%，结果表明采用辨识材料参数的轮胎模型在垂向特性与实际轮胎相符合，证明了基于材料参数辨识的矿用自卸车轮胎有限元模型垂向特性的准确性。

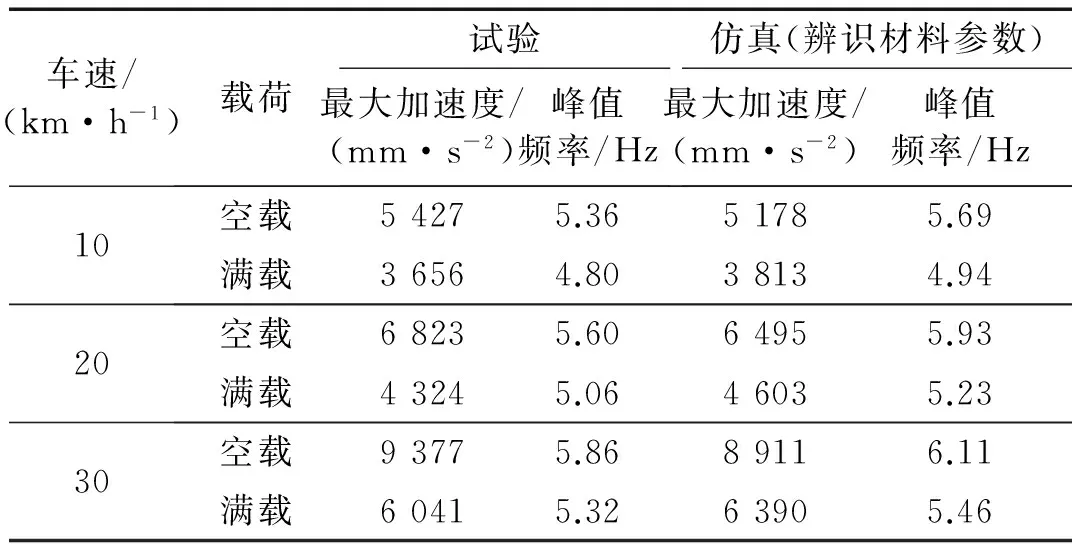
表4　不同车速、载荷下轮胎仿真与试验对比

5　结　论

(1)矿用自卸车轮胎材料参数难以获取，本文提出利用扩展卡尔曼优化的BP神经网络对轮胎材料参数进行辨识的方法。该方法利用脉冲工况仿真得到的轮胎垂向加速度辨识材料参数，网络预测输出与期望输出误差不超过±2%，表明该方法对材料参数具有较好的辨识能力。

(2)针对脉冲工况试验数据包含大量噪声，以至于无法得到合理且有效的脉冲数据，本文使用db13小波对信号进行去噪处理，在消除高频噪声的同时，保留所需的低频信号，取得了良好的去噪效果。

(3)通过采用辨识材料参数的轮胎模型在不同车速、载荷下仿真数据与试验数据的对比，证明了基于材料参数辨识的矿用自卸车轮胎有限元模型垂向特性的准确性。

[1]石琴,陈无畏,洪洋,等.基于有限元理论的轮胎刚度特性的仿真研究[J].系统仿真学报,2006,18(6):1445-1449.

SHI Qin,CHEN Wuwei,HONG Yang,et al.The simulation of tire’s stiffness characteristics using finite element model[J].Journal of System Simulation,2006,18(6):1445-1449.

[2]张德丰.MATLAB神经网络应用设计[M].北京:机械工业出版社,2012.

[3]YAM J Y F,CHOW T W S.A weight initialization method for improving training speed in feedforward neural network [J].Neurocomputing,2000,30(1):219-232.

[4]谢延敏,王新宝.基于灰色理论和GA-BP 的拉延筋参数反求[J].机械工程学报,2013,49(4):44-50.

XIE Yanmin,WANG Xinbao.Parameter inverse problem for drawbeads based on the gray theory and GA-BP[J].Journal of Mechanical Engineering,2013,49(4):44-50.

[5]PICHLER B,MANG H A.Parameter identification based on first order approximation neural networks[J].PAMM,2003,2(1):440-441.

[6]GUARNERI P,ROCCA G,GOBBI M.A neural-network based model for the dynamic simulation of the tire/ suspension system while traversing road irregularities [J].Neural Networks,IEEE Transactions on,2008,19(9):1549-1563.

[7]于德介,雷慧.一种基于神经网络的结构参数识别方法[J].湖南大学学报,1999,26(4):39-43.

YU Dejie,LEI Hui.A method for structural parameters identification using neural networks[J].Journal of Hunan University,1999，26(4):39-43.

[8]SIMON D.Training radial basis neural networks with the extended kalman filter[J].Neurocomputing,2002,48(1):455-475.

[9]胡林,谷正气,黄晶,等.30.00 R51 子午线轮胎刚度仿真[J].系统仿真学报,2008,20(8):2210-2214.

HU Lin,GU Zhengqi,HUANG Jing,et al.30.00 R51 radial tire stiffness simulation [J].Journal of System Simulation,2008,20(8):2210-2214.

[10]程冬冬.子午线轮胎三维精细网格有限元分析[D].上海：东华大学,2014.

[11]蒋霖,文鸿雁.基于 EKF 的神经网络在变形预测中的应用[J].桂林工学院学报,2006,26(1):66-68.

JIANG Lin,WEN Hongyan.Application of neural network based on the extended Kalman filter to deformation prediction[J].Journal of Guilin University of Technology,2006,26(1):66-68.

[12]付梦印,邓志红,张继伟.Kalman 滤波理论及其在导航系统中的应用[M].北京：科学出版社,2003.

[13]庄继德.汽车轮胎学[M].北京：北京理工大学出版社,1996.

[14]薛雪.车辆轮胎与土壤接触变形的有限元分析[D].杨凌：西北农林科技大学,2010.

[15]程冬冬.子午线轮胎三维精细网格有限元分析[D].上海：东华大学,2014.

[16]HICKERNELL F.A generalized discrepancy and quadrature error bound[J].Mathematics of Computation of the American Mathematical Society,1998,67(221):299-322.

[17]BRITO N S D,SOUZA B A,PIRES F A C.Daubechies wavelets in quality of electrical power[C]//Harmonics and Quality of Power Proceedings,1998.Proceedings.8th International Conference On.IEEE,1998,1:511-515.

[18]郭亚.振动信号处理中的小波基选择研究 [D].合肥:合肥工业大学,2003.

[19]姜永胜,王其东.汽车振动信号后处理的研究 [D].合肥：合肥工业大学学报,2006.

Tire material parametric identification of mining dump trucks based on EKF-BP

ZHANG Feifei1,GU Zhengqi1,2,ZHANG Sha1,MA Xiaokui1,ZHU Yifan1

(1.State Key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University,Changsha 410082,China；2.Hunan University of Arts and Science,Changde 415000,China)

Tire material parameters are very important to tire finite element model,but tire materials are many and their structure is complex,so tire material parameters are difficult to acquire.The method using BP neural network optimized with the extend kalman filter (EKF)to identify tire parameters was proposed.The dynamic simulation of tire impulse condition was simulated based on tire finite element model,The tire vertical acceleration obtained with simulation was regarded as an ideal input sample of a BP neural network,and the tire material parameters needed to identify were regarded as ideal output samples of the BP neural network,then the nonlinear mapping network model between them was built with network trainings.The tire vertical acceleration test data were denoised with wavelet and inputted into the trained network,then the tire material parameters were identified effectively.Through comparing simulation data with the tested ones under corresponding conditions,it was shown that the biggest error is 6.45%; the correctness of vertical characteristics of tire finite element model based on identification of material parameters is verified.

mining dump truck tire; parametric identification; BP neural network; extend Kalman filter (EKF); wavelet denoise

国家高技术研究发展计划(863计划)(2012AA041805)；中央财政支持地方高校专项资金项目-创新团队(0420036017)；湖南大学汽车车身先进设计与制造国家重点实验室自主课题资助项目(734215002)

2015-06-16修改稿收到日期：2015-08-25

张菲菲 女，硕士，1991年9月

谷正气 男，博士，教授，1963年12月

TD57

A DOI:10.13465/j.cnki.jvs.2016.17.012