单人Bounce荷载的实验建模研究

王　磊，陈　隽,2，楼佳悦，李　果

(1.同济大学 结构工程系，上海　200092；2.同济大学 土木工程防灾国家重点试验室，上海　200092)



单人Bounce荷载的实验建模研究

王磊1，陈隽1,2，楼佳悦1，李果1

(1.同济大学 结构工程系，上海200092；2.同济大学 土木工程防灾国家重点试验室，上海200092)

Bounce指音乐会或体育比赛中常见的观众双脚不离地的身体有节奏的上下往复运动。利用测力板以及无线测力鞋垫，开展了单人在不同频率下的Bounce荷载的测试试验，共得到了109人次822条有效单人Bounce荷载记录。在此基础上，建立了Bounce荷载的傅里叶级数模型，给出了四阶动载因子和相位角的建议值，并与国外已有模型进行了对比分析。本文模型所模拟的Bounce荷载与实测荷载的时域特性相同，所引起的结构响应幅值一致，可供工程设计参考使用。

Bounce荷载；大跨楼盖；傅里叶级数模型；动载因子

随着建筑材料性能与设计水平的不断提高，以及建筑功能的多元化需求，建筑楼盖结构的跨度越来越大。另一方面，经济的发展带来社会文化生活的丰富，人们参加各种音乐会和大型体育活动的次数迅速增多。媒体报道2013年中国演出市场的总经济规模为463亿元，而在2009年只有约25亿的规模，四年增长了18倍。在欣赏音乐会和现场比赛的过程中，观众随着音乐或比赛进程的有节奏运动非常常见。当人群有节奏运动的频率与支撑结构的自振频率相当时，共振效应会造成支撑结构的过大振动，一方面可能造成结构的破坏，另一方面可能造成观众的身体不适和心理恐慌，甚至诱发公共安全事件。如1985年瑞典的Nya Ullevi体育场在举行音乐会时，看台上的观众随音乐的节奏性运动引起体育场下软土地基的振动，在400 m外都可感受到，体育场基础遭受到了严重损坏[1]。

Bounce(有学者称为Bobbing)指双脚不离地的人体上下往复运动，是有节奏运动中最为常见的运动形式。尤其是在音乐厅和体育场等场所，由于活动空间有限，位置固定，人们常常伴随音乐节奏做Bounce运动。Bounce运动相对于跳跃等剧烈行为更省力，持续时间更长，造成结构共振的可能性也就更大[2]。因此，国外有规范建议将Bounce作为体育场馆和音乐会场的建筑楼盖振动分析的代表性动力荷载[3-4]。可靠的荷载模型是保障结构分析准确性的基本前提，国外一些学者已对bounce荷载进行了研究,AGU等采用测力板进行了Bounce荷载试验，结果与丹麦规范[3]建议的荷载模型进行了分析比较，实测值超出规范值3倍，并指出前3～4阶谐波频率有影响[5]。YAO[6]设计了一个模拟看台的可调整刚度的试验装置，研究Bounce荷载下的人与结构相互作用影响。PARKHOUSE等[7]利用测力板进行人群Bounce荷载试验，研究人群荷载的随机性和协同性，试验给出了不同人数下人群Bounce的整体前四阶动载因子。DUARTE等[8]通过混凝土简支梁在Bounce荷载下的位移响应，反推获得了Bounce荷载模型的各阶动载因子。对于Bounce荷载，国内开展的研究不多，目前也尚没有相应的荷载模型或取值建议。

对此，本文通过试验获得了大量单人Bounce荷载记录，在此基础上建立了4阶傅里叶级数模型，给出了模型参数的取值方法，与国外已有研究成果进行了比较，并与实测荷载在时程和结构响应上进行了对比验证。

1　Bounce荷载试验数据

数量多且频谱成分丰富的Bounce荷载实测记录是建立荷载模型的前提。本研究收集到了两批实测Bounce荷载数据，一批来自英国的谢菲尔德大学的试验，另一批来自同济大学的试验。

谢菲尔德大学的试验利用固定于刚性地面的测力板(AMTI BP-400600,USA，图1(a))开展，共84人参加。试验Bounce频率范围为1.5～3.6 Hz，按0.3 Hz递增，每人共8个试验工况。试验者根据节拍器的引导完成每个工况。每次测试持续30 s，采样频率为200 Hz。测试者在每次测试结束后休息至无疲惫感后才开始进行下一个工况的试验。谢菲尔德试验共获得了672条连续Bounce荷载时程。

同济大学试验采用德国Novel公司的Pedar高精度无线测力鞋垫技术，见图1(b)。这种技术广泛应用于运动医学的测力试验中。该技术采用嵌入鞋内垫的压力传感器，实时反映足底压力分布，连续记录运动状态下的足底压力，具有和传统测力板技术相同的测试精度和测试质量。迄今共有25人参与了试验，Bounce频率范围为1.5～3.5 Hz，中间按0.4 Hz递增，每人有6个试验工况。每次测试持续25 s左右，采样频率100 Hz。试验者同样按节拍器引导完成每个试验工况，结束后休息至无疲惫状态才进行下一次的试验。同济试验获得了150条连续Bounce荷载时程。

图1　Bounce荷载试验情况Fig.1　Experimental test for Bounce loads

两批试验总共822条单人Bounce荷载记录，为目前文献报道中数量最多的数据库。图2是某测试者在低频、中频、高频下的Bounce荷载名义力(竖向力/体重)时程及其分别对应的傅里叶幅值谱。可见，三种不同快慢频率下，Bounce时程在峰值和波形形状上有很大不同。频谱上，前3～4个峰值比较明显，分别对应Bounce频率及其倍频，随着Bounce频率的增大，倍频处的峰值慢慢变小而主频处的峰值越来越大。以上试验记录的时频域特点与AGU等[5]的试验描述一致。

(a) Bounce频率1.5Hz(b) Bounce频率1.5Hz(c) Bounce频率2.7Hz

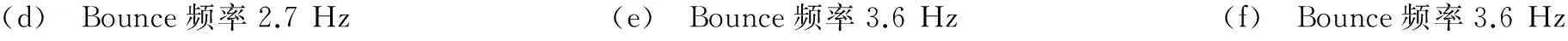
(d) Bounce频率2.7Hz(e) Bounce频率3.6Hz(f) Bounce频率3.6Hz

图2实测Bounce荷载曲线及其傅里叶幅值谱
Fig.2 Experimentally measured Bounce load curves and their Fourier amplitude spectra

2　Bounce荷载模型

2.1傅里叶级数模型

傅里叶级数模型是描述周期性荷载的常用数学工具，广泛用于描述行走、跳跃等人致荷载[9-12]。Bounce运动也可合理地假定为周期性重复过程，则荷载的傅里叶级数模型为：

(1)

式中:F(t)代表的是竖向Bounce荷载；G为人的静止体重；αi为竖向第i阶傅里叶系数，也称为动载因子(Dynamic Loading Factor,DLF)；fp为bounce频率；φi为竖向第i阶谐波相位角，取值范围[-π,π]；n为模型中考虑的阶数。

根据对Bounce数据库记录的分析，4阶以上的谐波分量的DLF值很小，从保证精度同时方便使用的角度，取模型截断阶数n=4。对数据库中每一条Bounce记录作傅里叶变换得到对应的幅值谱和相位谱，从中可获得各阶DLF及相位。在确定每一阶DLF以及相位时将其频率搜索范围定为(n-0.5)fp～(n+0.5)fp，范围内幅值谱最大值取为此阶的DLF，对应频率作为此阶的实际频率。例如Bounce工况的频率为2.0 Hz时，一阶和二阶的频率范围分别定为1.0～3.0 Hz和3.0～5.0 Hz。图3是某条记录的傅里叶幅值谱

和相位谱，星号标出的点代表的是各阶的DLF和相位。

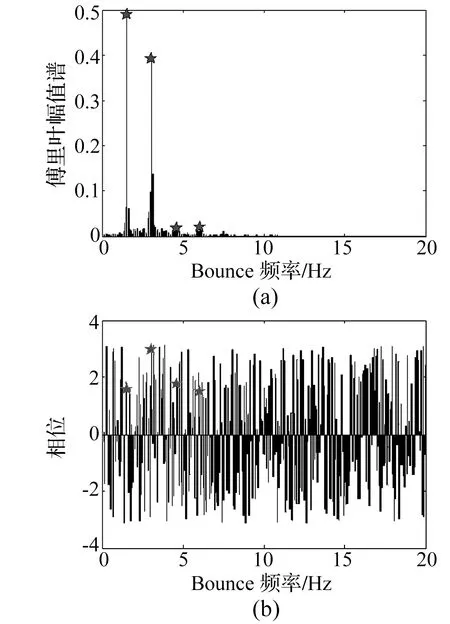
图3　某时程的傅里叶幅值谱和相位谱Fig.3　The Fourier amplitude and phase spectra of one time history

2.2动载因子取值

通过上述的方法对数据库中的822条荷载时程进行分析处理得到前四阶的DLF以及对应的实际频率值。各阶DLF在各频率范围内的分布如图4所示。

图4　前四阶DLF随Bounce频率的变化Fig.4　The change of the first four dynamic load factors with the frequency of Bounce

分析结果显示Bounce的各阶DLF分布相对于步行的各阶DLF分布更加离散[9-11]。为了更清楚地了解各阶DLF随频率的变化趋势。对横轴的Bounce频率进行分区统计，共分成8个频率区段，分别为：(0,1.65)Hz；(1.65,1.95)Hz；(1.95,2.25)Hz；(2.25,2.55)Hz；(2.55,2.85)Hz；(2.85,3.15)Hz；(3.15,3.45)Hz；(3.45,5)Hz。计算各个区段内各阶DLF的平均值及标准差，对各阶DLF均值和均值±1倍标准差随频率的变化进行最小二乘曲线拟合，得到的图形曲线见图4。图中星星符号代表频段均值，三角形代表一倍标准差，均值拟合所得回归方程见表1。可以看出，一阶DLF随频率增加而缓慢上升，二、三、四阶则都随频率缓慢下降，这一趋势与前文中对图2的描述相一致。

表1　各阶动载因子回归方程

2.3相位角取值

数据分析结果发现，前四阶的相位角或者是各阶间的相位差都非常离散，与Bounce频率无明显的关系，因此将一阶相位角取为0，第2～4阶相位角取为-π/3，π/3和0，分别是相位差试验结果均值。

3　模型对比和验证

3.1不同模型DLF对比

国外有关Bounce的荷载模型有限，最具代表性的是丹麦1998年颁布的荷载设计规范[3]和Duarte的荷载模型[8]，PARKHOUSE[7]没有给出具体模型但给出了不同人数、不同频率下的实测DLF。表2列出了上述研究所给出的动载因子。

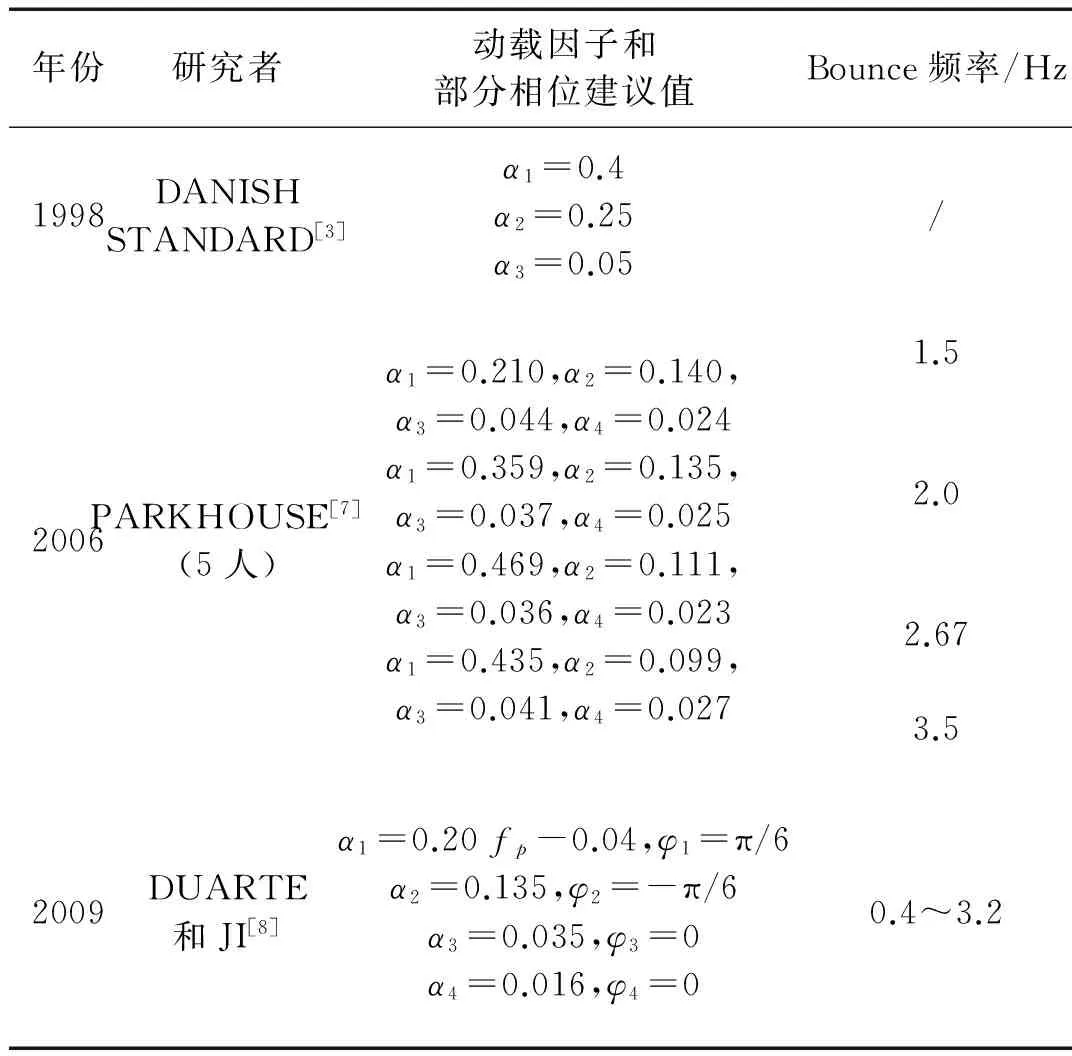
表2　不同研究者提出的荷载模型

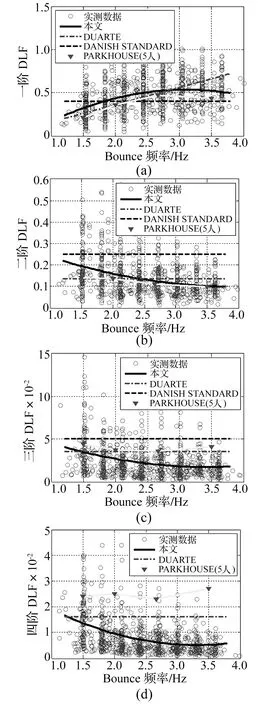
图5　不同模型各阶动载因子比较Fig.5　Comparison of DLFs from different models for each order

图5是本研究所提DLF与已有模型的对比。图中可见本文模型和Duarte模型一阶的DLF在1.5～3 Hz范围内比较接近。由于本研究数据的测试频率范围1.5～3.6 Hz高于DUARTE试验的0.4～3.2 Hz，因此高频段DLF的取值比DUARTE模型更有依据。试验过程中发现，测试者在高频bounce时很难跟得上节拍器的频率，这正是一阶DLF在高频处不再随频率增加的主要原因。而这一点也与PARKHOUSE通过试验数据生成的5人bounce的整体一阶DLF变化趋势相同。PARKHOUSE的5人bounce其整体一阶DLF相比于本文和Duarte的一阶DLF都要小，这是因为多人bounce并不是完全同步的，存在一定的随机性。对于二阶DLF本文模型的变化趋势与PARKHOUSE的5人bounce的整体二阶DLF变化大致相当。三阶和四阶对于荷载模型其贡献比较少，各模型间三阶和四阶DLF随频率的变化虽不是特别接近，但整体上还是保持在同一数量级上。对于相位，丹麦规范和PARKHOUSE均未给出具体的取值，DUARTE则直接采用了文献[12]中跳跃荷载前两阶的相位角，三、四阶相位角均取为0。

3.2模型时程对比

图6是本文和Duarte两种模型构造的名义力荷载(竖向力/体重)时程曲线在低频和高频下与实测名义力时程的对比。图中可以发现，本文的模型在形状上与实测时程比较接近，幅值范围上与实测时程存在一些差异。这是由DLF计算时忽略了主谐波频率邻近的能量所造成的，但由于实际设计中一般采用共振假定，周期性的模拟荷载会引起较大的振幅，弥补了DLF偏小的问题。本文接下来将从响应上对模型进行对比验证。

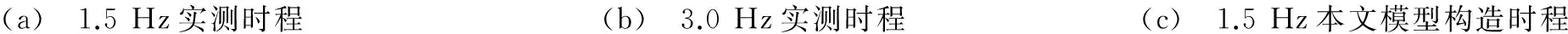
(a) 1.5Hz实测时程(b) 3.0Hz实测时程(c) 1.5Hz本文模型构造时程

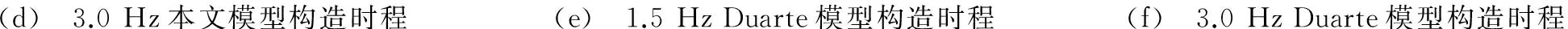
(d) 3.0Hz本文模型构造时程(e) 1.5HzDuarte模型构造时程(f) 3.0HzDuarte模型构造时程

图6 不同模型时程曲线和实测时程曲线比较
Fig.6 Comparison of time history curves for different models and experimentally measured Bounce load curves

3.3模型响应对比和验证

将图6中的1.5 Hz实测和仿真时程、3.0 Hz实测和仿真时程分别施加于基频为3.0 Hz、阻尼比为0.02的单自由度体系，计算结构的加速度响应，如图7所示。图中的横线是仿真时程输入后结构的最大加速度响应，可以看出，无论是一阶共振响应还是二阶共振响应，本文的荷载模型构造的荷载与实测荷载比较吻合，能够满足工程应用的需要。

(a) 仿真1.5HzBounce输入(b) 实测1.5HzBounce输入

(c) 仿真3.0HzBounce输入(d) 实测3.0HzBounce输入

图7 不同激励下单自由度结构的加速度响应
Fig.7 Acceleration response of the single degree of freedom structure in different input force

4　结　论

利用测力板和无线测力鞋垫技术获得了822条不同频率的单人bounce荷载时程。通过这些数据并基于傅里叶级数模型，提出了单人bounce荷载下的前四阶动载因子及相位角的建议值。通过与国外文献和规范已有模型的对比，以及仿真时程与实测记录的对比表明，可供工程设计与分析参考使用。

致谢 感谢英国谢菲尔德大学土木和结构工程学院Vitomir Racic博士(现意大利米兰理工大学)所提供的试验数据。

[1]BODARE A,ERLINGSSON S.Rock music induced damage and vibration at nya ullevi stadium [C]//Third international conference on case histories in geotechnical engineering (1993:June 1-4; St.Louis,Missouri).1993:Missouri S&T (formerly the University of Missouri—Rolla).

[2]JONES C A,REYNOLDS P,PAVIC A.Vibration serviceability of stadia structures subjected to dynamic crowd loads:A literature review [J].Journal of Sound and Vibration,2011,330(8):1531-1566.

[3]Dansk Standard DS 410,Code of practice for loads for the design of structures[S].Denmark,1998.

[4]IStructE/DCLG/DCMS Joint Working Group.(2008).Dynamic performance requirements for permanent grandstands:recommendations for management design and assessment[S].London,UK.

[5]AGU E,KASPERSKI M.A statistical approach to loads induced by bobbing [C]//Structural Dynamics EURODYN,2008.

[6]YAO S,WRIGHT J R,PAVIC A,et al.Experimental study of human-induced dynamic forces due to bouncing on a perceptibly moving structure [J].Canadian Journal of Civil Engineering,2004,31(6):1109-1118.

[7]PARKHOUSE J G,EWINS D J.Crowd-induced rhythmic loading[J].Proceedings of the ICE-Structures and Buildings,2006,159(5):247-259.

[8]DUARTE E,JI T.Action of individual bouncing on structures [J].Journal of Structural Engineering,2009,135(7):818-827.

[9]KERR S C,BISHOP N W M.Human induced loading on flexiblestaircases[J].Engineering Structures,2001,23(1):37-45.

[10]陈隽,彭怡欣,王玲.基于步态分析技术的三向单足落步荷载曲线试验建模[J].土木工程学报,2014,47(3):79-87.

CHEN Jun,PENG Yixin,WANG Ling.Experimental investigation and mathematical modeling of single footfall load using motion capture technology [J].China Civil Engineering Journal,2014,47(3):79-87.

[11]陈隽,王浩祺,彭怡欣.行走激励的傅里叶级数模型及其参数的试验研究[J].振动与冲击,2014,33(8):11-15.

CHEN Jun,WANG Haoqi,PENG Yixin.Experimental investigation on fourier-series model of walking load and its coefficients [J].Journal of Vibration and Shock,2014,33(8):11-15.

[12]JI T,ELLIS B R.Floor vibration induced by dance-type loads:theory[J].The Structural Engineer,1994,72:37-44.

Modeling with tests for single human bounce load

WANG Lei1,CHEN Jun1,2,LOU Jiayue1,LI Guo1

(1.Department of Structural Engineering,Tongji University,Shanghai 200092,China;2.State Key Laboratory of Disaster Reduction in Civil Engineering,Tongji University,Shanghai 200092,China)

Bounce means up-down movements of human body with two feet remaining on the ground,it is a typical activity of audience in a concert or sport game.Tests were conducted to measure a single person’s bouncing load with different frequencies using a force plate and a wireless dynamometer insole.109 persons participated in tests to generate 822 individual bouncing load records.A fourth-order Fourier series model was built to describe the bounce load,whose coefficients called dynamic load factors and phase angles were determined with the statistical analysis of measured records.The proposed model was compared with other available models according to model parameters in time domain.It was shown that simulated bounce load curves with the proposed model have similar shapes to those of the measured loads; the responses of a single-DOF system to simulated and measured bounce loads,respectively are nearly the same.

human bounce load; long span floor; Fourier series model; dynamic load factor

国家自然科学基金(51478346)

2015-04-17修改稿收到日期：2015-08-31

王磊 男，硕士生，1992年9月生

陈隽 男，教授，博士生导师，1972年4月生

E-mail：cejchen@tongji.edu.cn

TU312+.1

A DOI:10.13465/j.cnki.jvs.2016.17.009