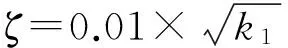非弹性碰撞振动系统的首次穿越分析
徐 明,金华斌
(1.中国计量学院计量测试工程学院,杭州 310018;2.浙江省流量计量技术研究重点实验室,杭州 310018)
非弹性碰撞振动系统的首次穿越分析
徐明1,2,金华斌1,2
(1.中国计量学院计量测试工程学院,杭州310018;2.浙江省流量计量技术研究重点实验室,杭州310018)
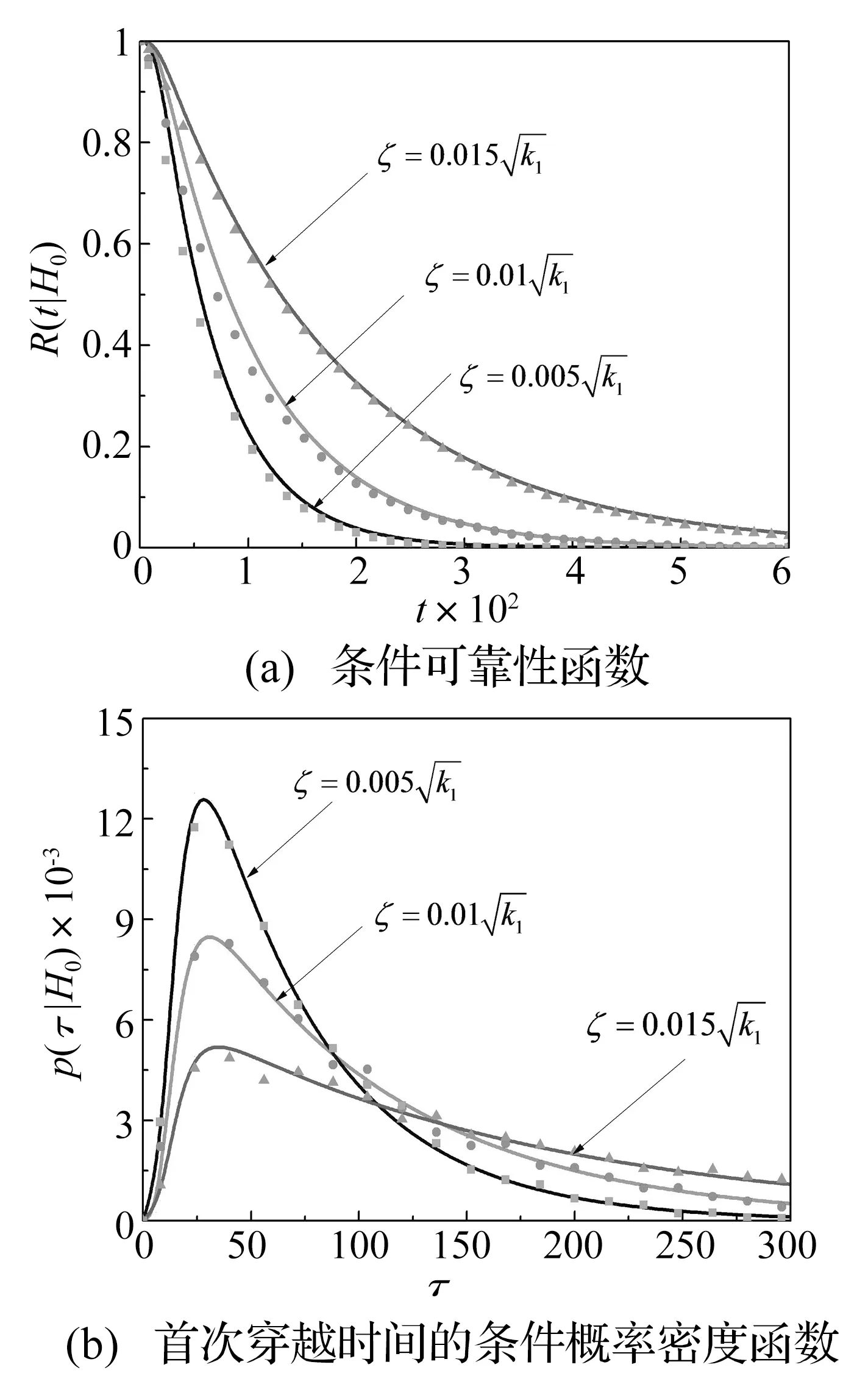
对高斯白噪声激励作用下的非弹性碰撞振动系统的首次穿越问题作了分析,得到了非弹性碰撞振动系统的条件可靠性函数和相应的条件概率密度函数。不同于以往碰撞物理模型,非弹性碰撞作用采用了修正赫兹接触模型。首先,基于能量耗散平衡法,将碰撞振动系统转化为不含碰撞的等效非线性系统。其次,应用基于系统能量的随机平均法,得到关于系统总能量的平均伊藤随机微分方程。然后,建立条件可靠性函数的控制方程及相应的初边界条件,并数值求解。最后,分析了不同系统参数情形下条件可靠性函数及相应的条件概率密度函数的变化规律。该方法可有效分析非弹性碰撞振动系统的首次穿越问题,数值分析结果表明较大的阻尼系数可提高系统可靠性,而较大的激励强度则往往增加发生首次穿越的概率。
非弹性碰撞振动系统;修正赫兹接触模型;随机平均法;条件可靠性函数;条件概率密度函数
在机械和结构工程中,碰撞振动系统是一类十分广泛的动力学系统,诸如石油运输管道碰撞其约束,大型轮船晃动时与冰山等障碍物间的相互撞击。碰撞振动系统对系统安全影响十分关键,因而已有不少学者对其进行研究[1-3]。由于自然界中存在着大量的不可避免的随机扰动,针对受随机激励作用的碰撞振动系统研究的文献也已有很多[4-6]。

基于该模型,应用随机平均法研究了单自由度碰撞振动系统的随机响应[9]。随机响应分析的一个重要意义在于,可以提供结构安全性和可靠性的直观评估。对结构安全性和可靠性的精确描述在数学上可归于首次穿越问题。如核工业中管道碰撞问题,被撞击管道的过大塑性变形将会导致泄漏,直接影响安全生产。因此可将该工程问题提炼为简单的振子碰撞挡板模型,以最大位移或者最大能量为衡量破坏的指标,研究其首次穿越问题。
本文应用能量耗散平衡法及随机平均法,研究了基于修正赫兹接触模型的碰撞振动系统的首次穿越破坏。通过随机平均法得到的关于系统总能量的平均伊藤随机微分方程,建立了条件可靠性函数的控制方程-后向Kolmogorov方程,并用有限差分法数值求解,将求解结果与蒙特卡罗模拟结果比较以验证该方法的有效性。数值分析表明,增加系统的阻尼和减弱激励强度均可提高机械和结构工程中随机碰撞振动系统的安全性。特别需要说明的是,本文不同于以速度、位移等系统状态为首次穿越破坏准则,而以系统总能量超过临界能量视为发生首次穿越破坏,这类似于以材料应变能而非变形作为强度破坏准则。
1 等效非线性系统
本文考虑右侧具有固定挡板的单自由度碰撞振动系统,如图1所示,其运动微分方程可表示为:
(1)


图1 单边约束的碰撞振动系统示意图Fig.1 Schematic of the vibrating system with one side barrier


(2a)

(2b)
式中:g+和g-分别表示加载阶段和卸载阶段曲线,x0表示弹性碰撞和非弹性碰撞位移临界值,k2,k3表示附加刚度,δr表示质量块平衡位置与挡板间的距离。a1,a2分别表示质量块在平衡位置右侧最大的位移,左侧的最大位移。
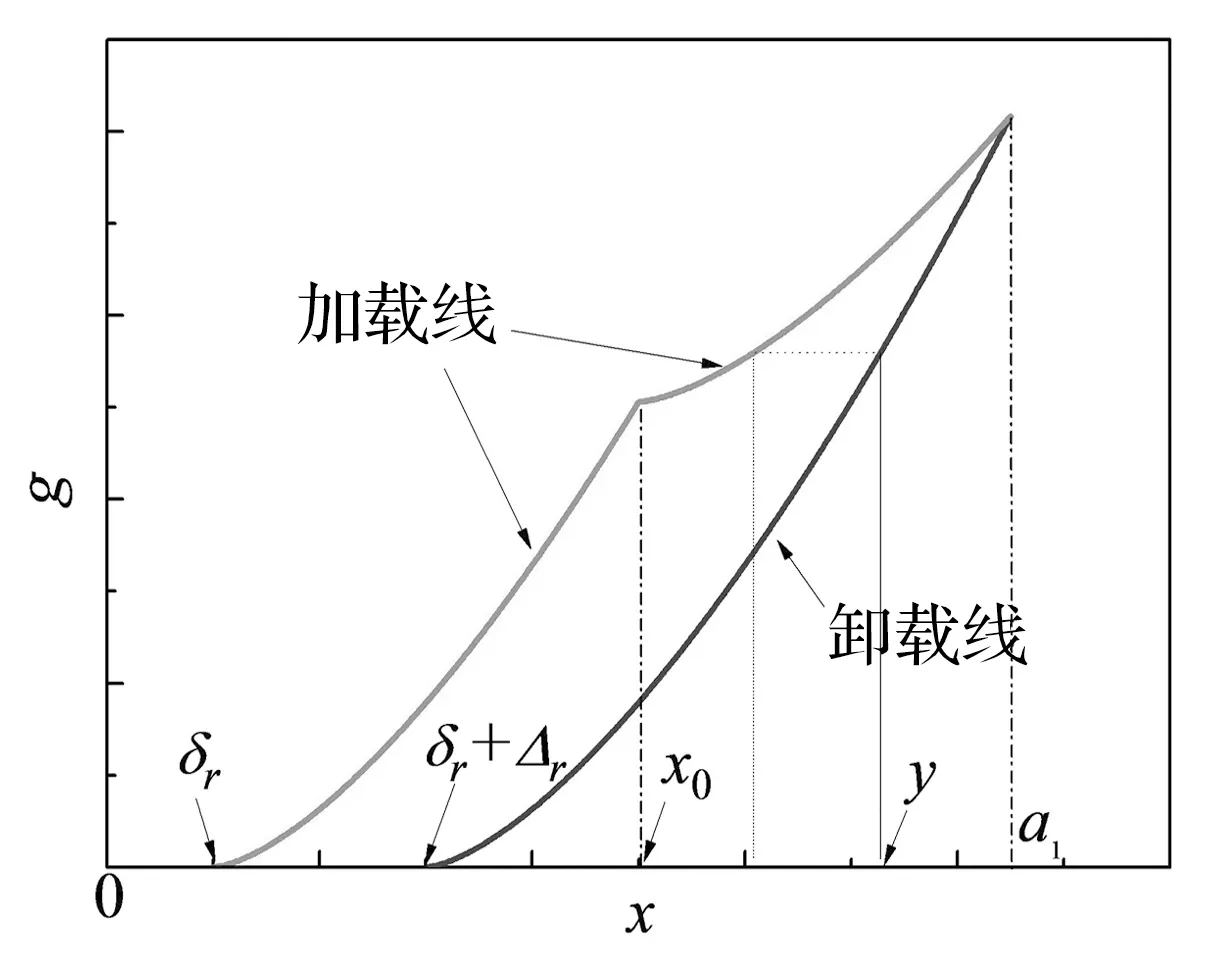
图2 修正赫兹接触模型力-位移曲线Fig.2 The constitutive relationship of the non-inelastic model
若碰撞过程发生仅出现可完全恢复的弹性变形,则加载和卸载曲线重合,碰撞接触力数学表达公式为:
(3)
由于修正赫兹接触模型表示的碰撞接触力同时包含阻尼和弹性效应,无法直接对该系统进行求解,故引入能量耗散平衡法,将碰撞作用力等效分解为阻尼和刚度两部分。阻尼表示为拟线性阻尼,刚度则表示成系统势能对位移的导数。拟线性阻尼由其在一个循环周期内的耗散能量与碰撞接触力耗散的能量相等来确定,相应的等效阻尼系数表达式为:
2ζ1(H)=
(4)
(5)
右侧位移幅值未超过临界值x0的情形(δr 2ζ1(H)=0 (6) 系统总势能则由其卸载能量确定,其相应的表达形式为: (7a) 式中:UL(x)=k1x2/2 (7b) 式中:y坐标对应的卸载阶段的碰撞作用力等于x坐标对应的加载阶段的碰撞作用力,y由关系式k2(y-δr-Δr)3/2=k3(x-x0)3/2+k2(x0-δr)3/2确定。 (7c) 对于情形δr (8a) 式中: (8b) 对于a1<δr情形,系统总势能仅存在于线性弹簧中,故而其表达式为: (9) 碰撞接触力分解为等效阻尼和等效刚度后,原系统(1)等效为下列非线性系统: (10) dH=m(H)dt+σ(H)dB(t) (11) 式中:B(t)是单位维纳过程。 与方程(11)相应的漂移系数m(H)和扩散系数σ2(H)分别为: (12a) (12b) 条件可靠性函数的控制方程为后向Kolmogorov方程,表达式为 (13) 式中:m(H0)和σ2(H0)可由将漂移系数m(H)和扩散系数σ2(H)中H替换为H0得到。 方程(13)的初始条件为 R(0|H0)=1,H0∈Ωs (14) 及相应的边界条件为 R(t|H0)=0,H0=Hc, R(t|H0)=finity,H0=0 (15a,b) 一般情况下,后向Kolmogorov方程很难得到解析的表达式,本文将采用有限差分法数值求解该方程。 首次穿越时间的条件概率密度则可由条件可靠性函数得到, (16) 图3 不同粘性阻尼系数的影响Fig.3 Influence of the viscous damping coefficient ζ 图4 不同激励强度2D的影响Fig.4 Influence of the excitation intensity 2D 由上述讨论可知,① 本文提出的方法具有较好的精度,能较好分析非弹性碰撞振动系统的首次穿越问题;② 通过提高系统的阻尼,减小激励强度能显著提高系统的可靠性,为碰撞振动系统可靠性设计提供一定的理论指导。 [1]谢建华,文桂林,肖建.两自由度碰撞振动系统分叉参数的确定[J].振动工程学报,2001,14(3):249-253. XIE Jianhua,WEN Guilin,XIAO Jian.Criteria of bifurcation parameters of vibro-impact system with two-degree-of-freedom [J].Journal of Vibration Engineering,2001,14(3):249-253. [2]赵文礼,周晓军.二自由度含间隙碰撞振动系统的分岔与混沌[J].浙江大学学报(工学版),2006,40(8):1435-1438. ZHAO Wenli,ZHOU Xiaojun.Bifurcation and chaos of impactvibration system with two degrees of freedom and clearance[J].Journal of Zhejiang University(Engineering Science),2006,40(8):1435-1438. [3]张有强,丁旺才.干摩擦对碰撞振动系统周期运动的影响分析[J].振动与冲击,2009,28(6):110-112. ZHANG Youqiang,DING Wangcai.Study on effect of dry friction on periodic motion of impact vibration system[J].Journal of Vibration and Shock,2009,28(6):110-112. [4]田海勇,刘卫华,赵日旭.随机干扰下碰撞振动系统的动力学分析[J].振动与冲击,2009,28(9):163-167. TIAN Haiyong,LIU Weihua,ZHAO Rixu.Dynamic analysis of a vibro-impact system with random disturbance[J].Journal of Vibration and Shock,2009,28(9):163-167. [5]刘中华,黄志龙,朱位秋.二自由度碰撞振动系统的随机响应[J].振动工程学报,2002,15(3):257-261. LIU Zhonghua,HUANG Zhilong,ZHU Weiqiu.Stochastic response of two-degree-of-freedom vibro-impact system[J].Journal of Vibration Engineering,2002,15(3):257-261.[6]JING H S,SHEU K C.Exact stationary solutions of the random response of a singe-degree-of-freedom vibro-impact system[J].Journal of Sound and Vibration,1990,141(3):363-373. [7]DIMENTBERG M F,IOURTCHENKO D V.Random vibrations with impacts:a review[J].Nonlinear Dynamics,2004,36(2/3/4):229-254. [8]MCMILLAN A J,ACEVES C M,SUTCLIFFE M P F.Moderate energy impact analysis combining phenomenological contact law with localised damage and integral equation method[J].International Journal of Impact Engineering,2012,43:29-39. [9]XU M,WANG Y,JIN X L,et al.Incorporating dissipated impact into random vibration analyses through the modified Hertzian contact model[J].ASCE Journal of Engineering Mechanics,2013,139(12):1736-1743. First-passage failure of a non-elastic vibro-impact system XU Ming1,2,JIN Huabin1,2 (1.College of Metrology & Measurement Engineering,China Jiliang University,Hangzhou 310018,China;2.Zhejiang Provincial Key Laboratory of Flow Measurement Technology,Hangzhou 310018,China) The first-passage failure of an inelastic vibro-impact system was studied here,and the conditional reliability function and the conditional probability density function of the system were derived.Being different from the traditional impact model,the modified Hertzian contact model was adopted for this system.Firstly,based on the energy dissipation balance technique,the inelastic vibro-impact system was converted into an equivalent nonlinear system without impact.Secondly,the averaged Ito stochastic differential equation was derived with the stochastic averaging method.Thirdly,the governing equation for the conditional reliability function was established and numerically solved under given initial and boundary conditions.Lastly,the influences of different system parameters on the system’s conditional reliability function and conditional probability density function were ananlyzed.It was shown that the proposed technique is very efficient and accurate for the first passage failure of the vibro-impact system; the weaker excitation intensity and the bigger damping coefficient enhance the system’s reliability. inelastic vibro-impact system; modified Hertzian contact model; stochastic averaging; conditional reliability function; conditional probability density function 国家自然科学基金青年项目(11402258);浙江省‘仪器科学与技术’重中之重学科人才培育计划项目(JL150511) 2015-05-19修改稿收到日期:2015-08-09 徐明 男,博士,1986年生 O322;O324 A DOI:10.13465/j.cnki.jvs.2016.17.033

2 随机平均法

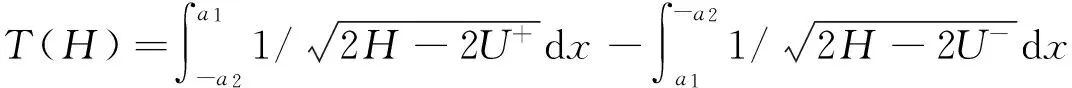
3 首次穿越破坏
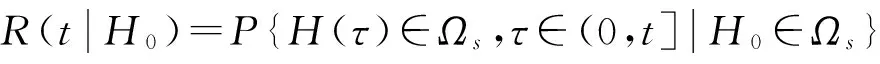
4 算例与讨论