高速铁路双线路基动应力的特性研究
张石友,孙海建,陈艳国
(1.河南省电力勘测设计院,郑州 450007;2.黄河勘测规划设计有限公司,郑州 450003)
高速铁路双线路基动应力的特性研究
张石友1,孙海建1,陈艳国2
(1.河南省电力勘测设计院,郑州450007;2.黄河勘测规划设计有限公司,郑州450003)
双线路基是高速铁路路基中常见的一种形式,其动应力的特性研究至关重要。建立了列车-轨道-双线路基三维有限元模型,并在两股钢轨上添加了两种典型的高低不平顺谱。通过数值计算,得到了两种轨道不平顺谱及三种列车运行速度下路基动应力沿纵向的分布,统计了不同深度处路基动应力的均值及变异系数,并给出了均值的拟合公式。最后,对两种轨道不平顺谱下路基动应力的概率分布型式进行了验证。利用柯尔莫哥洛夫检验方法,证明了轨道不平顺谱下路基动应力近似服从对数正态分布。
列车-轨道-双线路基有限元模型;轨道不平顺谱;路基动应力;变异系数;对数正态分布
高速铁路双线路基是目前应用较为广泛的一种路基形式[1]。由于轨道几何形状、尺寸和空间位置的偏差,高铁路基轨道沿高低方向具有一定的不平顺性。除了列车速度、列车轴重变化等影响因素外,轨道不平顺性对路基动应力的影响非常显著[2]。因此,轨道不平顺下高铁双线路基动应力的特性研究非常重要。
目前,对于列车荷载作用下路基动应力的研究主要有模型试验、数值模拟和现场实测三种手段。詹永祥等[3]以遂渝线为背景建立了1∶2室内路基模型,通过试验发现动应力沿路基面横断面方向上呈现“W”形分布,在混凝土底座处较大,在中点处和端部处相对较小。董亮等[4]通过轨道-路基三维有限元模型的数值分析,发现路基动应力沿路基面的横断面方向呈现抛物线分布;沿路基深度方向逐渐衰减,路基深度1.5 m处的动应力衰减为路基表面处动应力的一半。陈雪华等[5]对秦沈线进行了大量实测,统计发现路基动应力受列车速度显著影响,且沿着路基深度迅速衰减,并逐渐接近于静态应力值。范生波[6]根据武广线CRTⅠ型列车及CRTⅡ型列车作用下的路基动应力现场实测结果,统计发现动应力沿路基横断面方向呈现马鞍状分布,路基动应力沿深度方向呈现衰减趋势,在0.4 m、0.9 m、1.5 m及2.1 m深度处的衰减系数分别为0.71、0.57、0.52及0.32。
从上述可知,目前学者们对于列车荷载作用下路基动应力的研究多数都是确定性的,且都是针对于某一个断面。但是由于列车速度不同、列车轴重变化、轨道不平顺等因素的影响,沿线路方向各个位置处的路基动应力具有一定的随机性。刘扬[7]建立了车-轨道数值模型,计算得到了在三种典型的轨道不平顺状态下轮轨力的变异系数为0.05~0.15,并通过柯尔莫哥洛夫检验方法证明了轮轨力近似服从正态分布函数。中铁第四勘察设计院[8]对武广线试验段的现场实测结果进行了统计,发现路基动应力在轨道不平顺性、列车速度变化、轴重变化等因素的影响下,具有一定的变异性,变异系数为0.15~0.3。
本文通过ABAQUS软件建立了列车-轨道-双线路基模型,在双线路基两股钢轨上添加了两种典型的轨道不平顺谱。通过计算结果,统计了在不同列车速度下双线路基动应力均值及变异系数沿深度方向的分布。利用柯尔莫哥洛夫检验方法,证明了轨道不平顺下双线路基动应力均近似服从对数正态分布。本文的研究可为制定基于极限状态法的路基设计方法提供理论依据。
1 列车-轨道-双线路基三维有限元模型
列车-轨道-双线路基三维有限元模型主要包括列车模型、双轨道-双线路基模型、轨道不平顺谱的添加、阻尼边界设置等几个方面。
1.1列车模型
本文参照文献[9]建立了两系悬挂模型,如图1所示,列车类型则选用了CRH3型列车,列车的参数值[10-12]则表1所示。表中一系悬挂系统及二系悬挂系统分别连接转向架与轮对及车体与转向架。
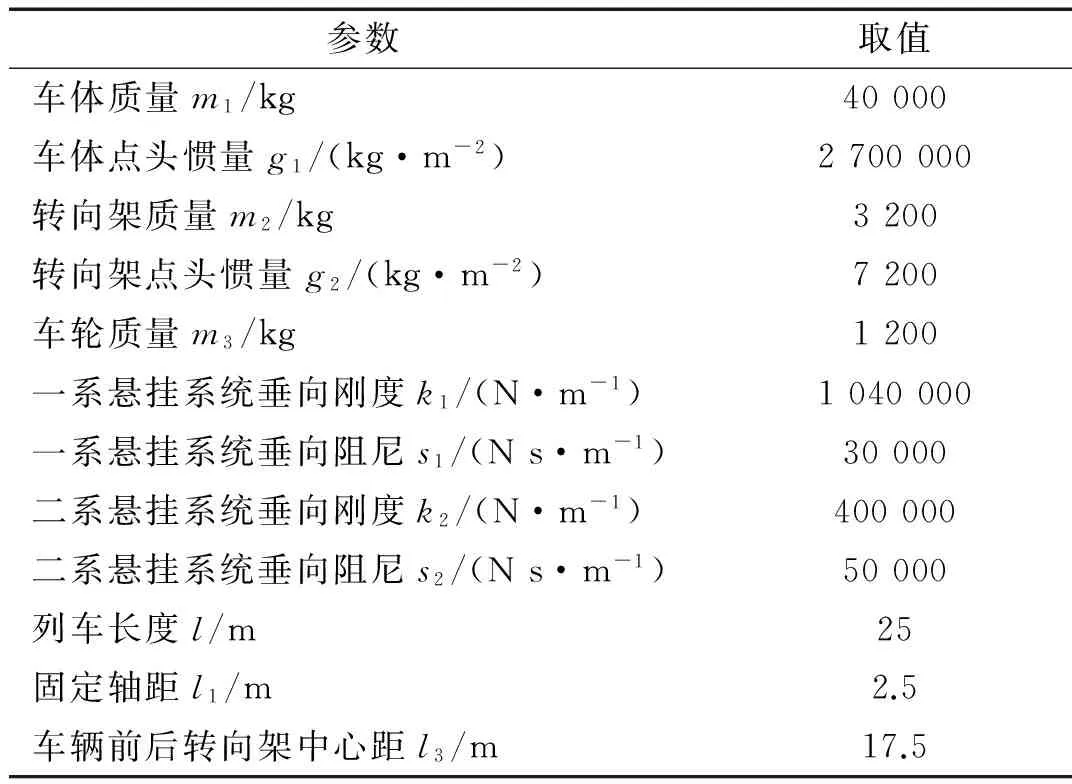
表1 列车模型模型参数
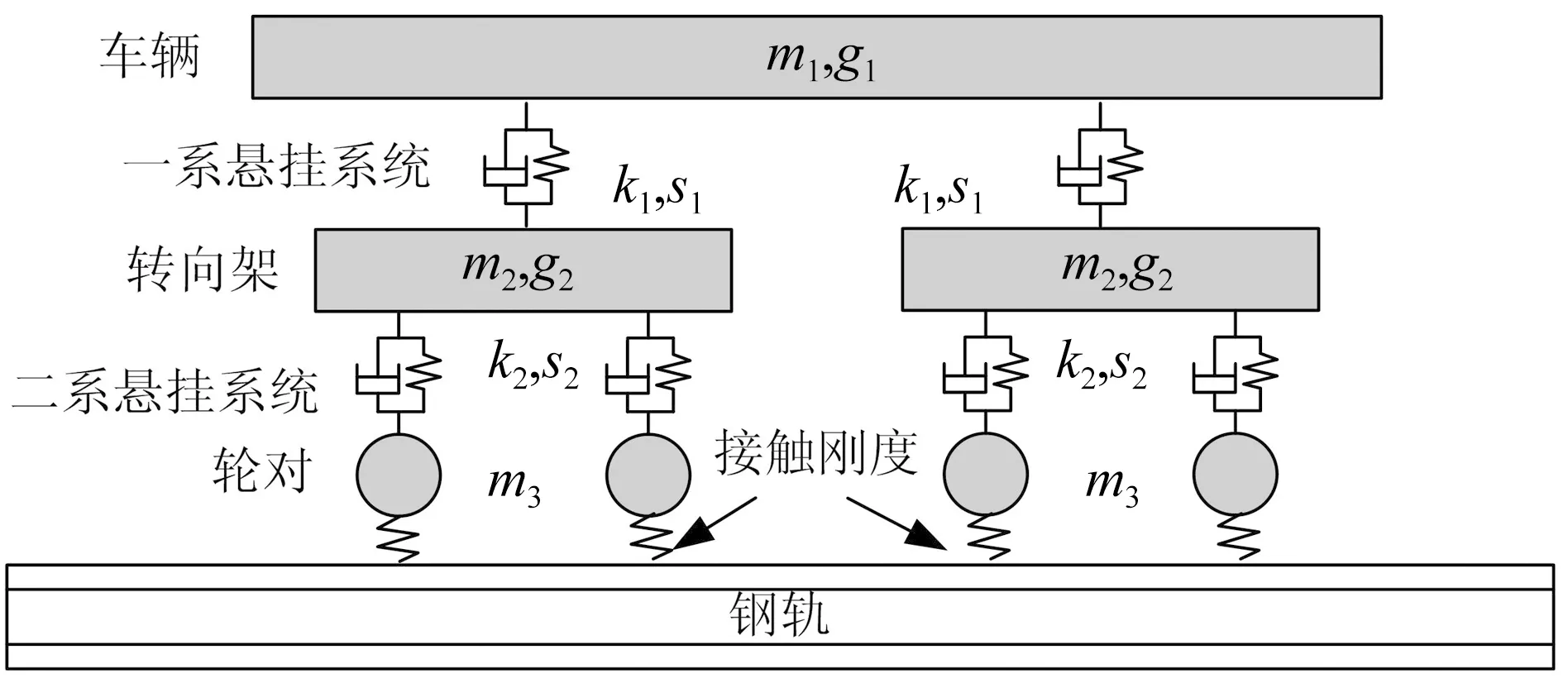
图1 两系悬挂列车模型Fig.1 Vehicle model with two stage suspension
1.2双轨道-双线路基模型
轨道系统从上到下由钢轨、扣件系统、轨道板、CA砂浆、混凝土底座组成;路基结构则由基床表层、基床底座及地基组成。钢轨采用等截面、均质的Ⅰ型直梁结构进行模拟,截面尺寸取UIC60标准断面尺寸。扣件系统采用弹簧阻尼系统进行模拟;混凝土底座、基床和地基部分采用8节点的实体单元模拟。表2给出了轨道系统及路基结构的相关参数[9,13]。
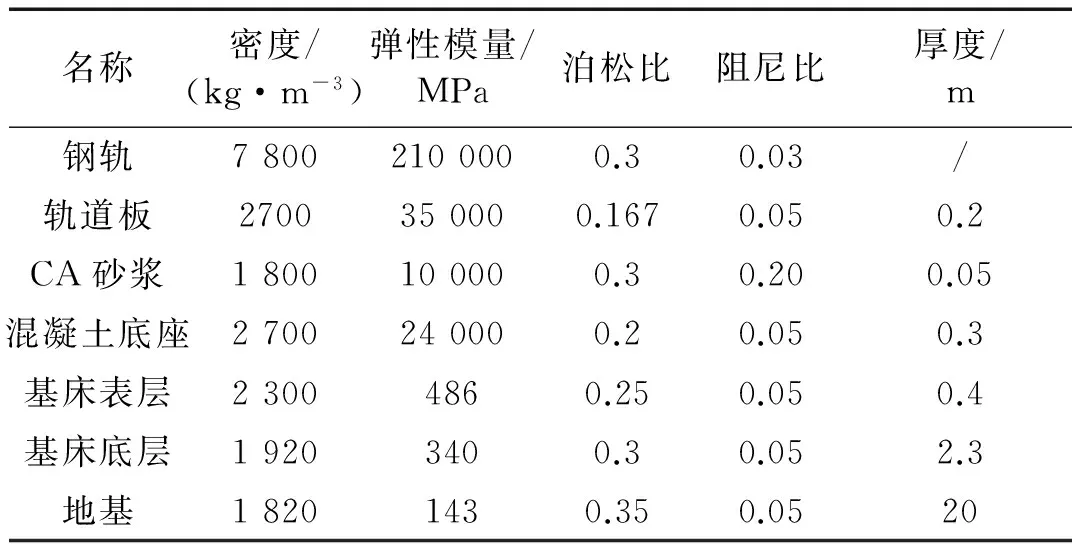
表2 双轨道-双线路基模型物理力学参数
1.3轨道不平顺谱
本文考虑了两种典型的轨道不平顺谱:德国低干扰谱与京津城际轨道不平顺谱。京津城际轨道不平顺谱通过实测获得;而德国低干扰的其高低不平顺的轨道谱密度函数[14]为:
(1)
式中:Sv(Ω)为轨道谱,cm2·m/rad;Ω为空间角频率,rad/m;Ωr,Ωc为截断频率,rad/m;Av为粗糙度常数m2·rad/m。
通过式(2)所示的三角级数法[15]可以将德国低干扰谱及京津城际轨道谱转化为沿纵向的不平顺空间分布,如图2所示。然后将这两种不平顺空间分布添加到钢轨表面上的各个单元节点上。
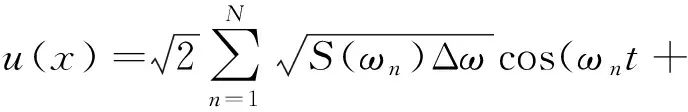
(2)
式中:u(x)为所采集的轨道不平顺样本;N为总采样点数;wn为采样频率;φn为在[0,2π]上均匀分布的相互独立的随机变量;S(wn)为不平顺功率谱密度函数。
1.4阻尼和边界设置
本文材料采用古典阻尼-瑞利阻尼[16]来表示,其定义为:
[C]=a0[m]+a1[k]
(3)
式中:a0为质量比例阻尼;a1为刚度比例阻尼。
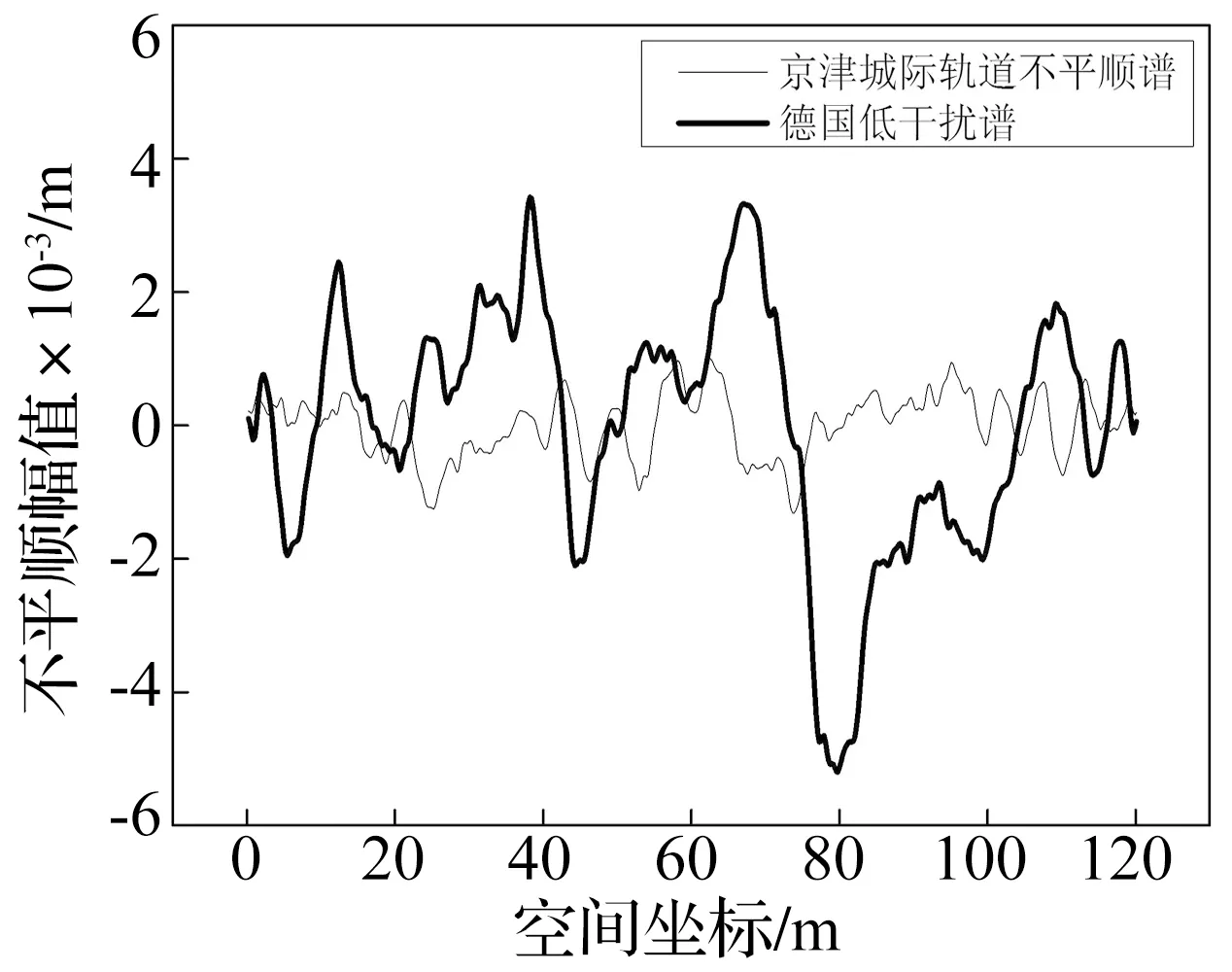
图2 两种典型轨道不平顺谱的空间分布Fig.2 Spatial distribution of two typical track irregularity spectrums
至于模型的边界问题,采用递减阻尼边界模式,边界处的阻尼设置为如图3所示的逐渐线性递增形式,从而波的能量则能够在边界处被逐渐吸收而不会产生反射。

图3 模型边界模式Fig.3 Border pattern of the model
1.5列车-轨道-双线路基有限元模型
建立了如图4所示的列车-轨道-双线路基有限元模型,其中列车模型采用4节车厢。计算模型中列车与轨道连接关系采用线性赫兹接触刚度进行描述,在一定程度上认为是准确的;钢轨与轨道板之间的扣件连接采用弹簧阻尼等效,数值取值根据扣件试验得到;轨道结构之间、轨道与路基之间可认为位移和力连续。由于动力作用下的土体应变实际上并不大,故采用线弹性本构模型。根据翟婉明[17],在移动荷载作用下的车辆-轨道耦合模型中,当轨道长度大于100 m,轨道结构的振动结果几乎不受影响,因此本文模型中的路基沿纵向长度取120 m,且中间60 m路基的网格加密。这个模型256 472个,节点数目302 341个。
图4 列车-双轨道-双线路基三维有限元模型断面图Fig.4 Cross sectionfor 3D finite element model of vehicle-double track-double subgrade
2 高铁双线路基动应力的特性研究
2.1三维有限元计算结果
图5给出了在德国低干扰谱和京津城际轨道谱及三种典型列车速度下路基面中心位置正下方0.2 m深度位置处节点的路基动应力沿纵向的分布。由图5可知,由于轨道不平顺性,同一路基深度处的动应力是不确定的,沿纵向的分布具有一定的随机性。在同一种轨道不平顺下,随着列车速度增加,路基动应力的随机性越来越明显;如在德国低干扰谱下,当列车速度为350 km/h时,路基动应力的范围是10.54 kPa~19.91 kPa;当列车速度为150 km/h时,路基动应力的变化范围是10.33 kPa~13.75 kPa。当列车速度相同时,德国低干扰谱下路基动应力的随机性比京津城际轨道不平顺谱下路基动应力的随机性更加明显;如当列车速度为350 kPa时,德国低干扰谱和京津城际轨道不平顺谱下路基动应力的变化范围分别是10.54 kPa~19.91 kPa和11.36 kPa~16.87 kPa。
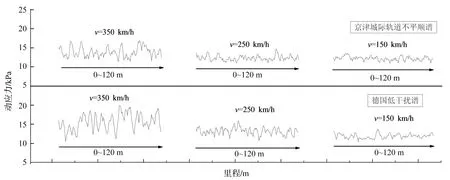
图5 路基动应力沿纵向的分布Fig.5 Distribution of dynamic stressof subgrade along longitudinal direction
2.2路基动应力的概率特性
根据数值模型网格的划分,这里统计了路基中心0.2 m、0.86 m、1.32 m、1.78 m及2.24 m深度处动应力沿纵向的均值和变异系数。
统计每个深度位置处的动应力时,沿纵向有272个节点,由于边界效应,去掉路基两端的各6个节点,因此每个深度位置处共统计260个节点处的动应力。根据概率统计知识及可靠度理论,路基动应力的均值、标准差及变异系数的统计公式分别为:
(4)

(5)
(6)
式中:μ(σd)、S*(σd)、COV(σd)分别为路基动应力σd的均值、标准差、变异系数;σdi为第i个节点处的动应力计算值。
由图6可知,在德国低干扰谱和京津城际轨道不平顺谱及三种列车运行速度下,路基动应力均值沿深度方向的衰减趋势基本一致,都近似呈现直线衰减。在同一种轨道不平顺谱下,列车速度越大,路基动应力均值越大,说明列车速度对路基动应力具有放大效应。而当列车速度相同时,在德国低干扰谱下的路基动应力均值比京津城际轨道不平顺谱下的路基动应力均值大,而德国低干扰谱的不平顺性更强,可知轨道不平顺性对路基动应力同样具有放大效应。此外,路基动应力均值沿深度的分布接近于武广线试验段实测结果[8],从而证明了该数值模型计算结果的可靠性。
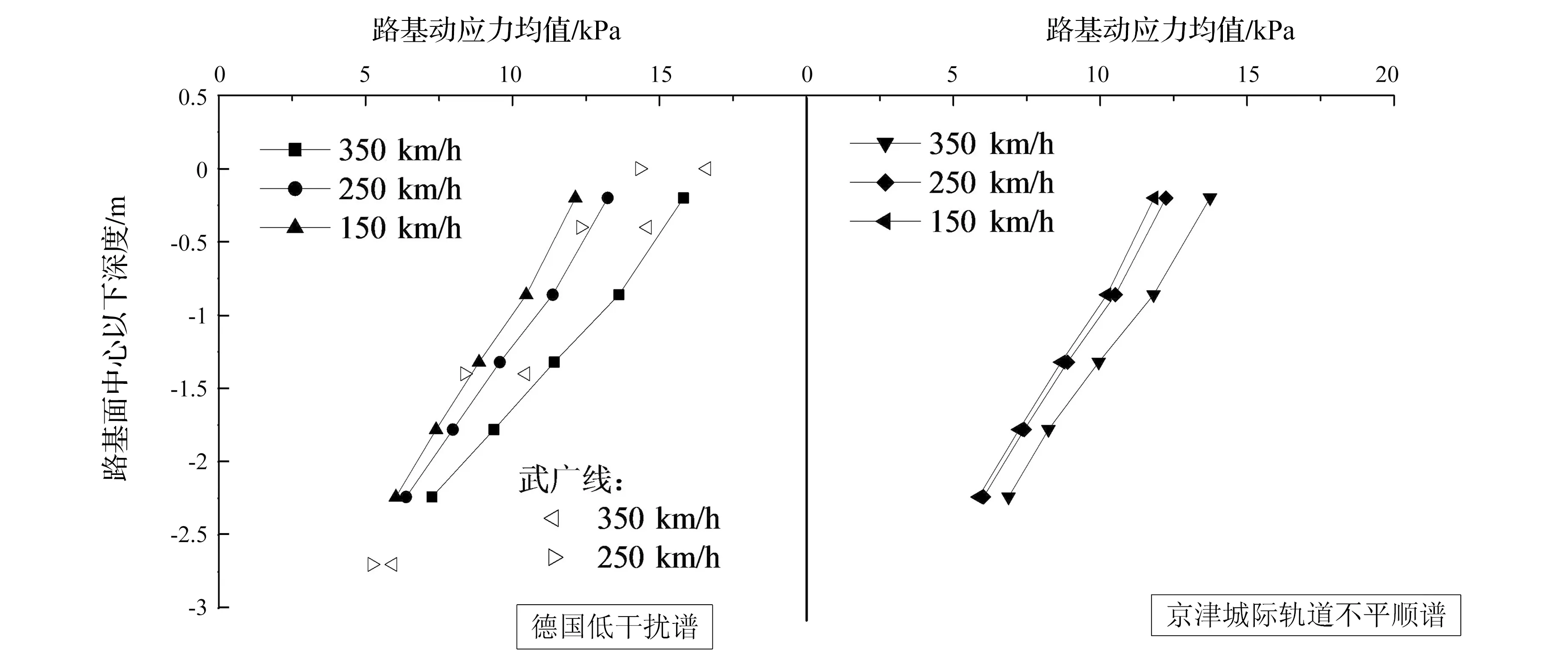
图6 路基动应力统计的均值Fig.6 Mean value of dynamic stress of subgrade
通过对路基动应力均值结果的拟合,可以得到在德国低干扰谱和京津城际轨道不平顺谱下,路基动应力均值沿深度方向的分布可分别利用式(8)和式(9)计算得到:
μ(σd)=6.6×(0.25h+1.1)×(1+0.003v)
(7)
μ(σd)=5.8×(0.25h+1.1)×(1+0.003v)
(8)
式中:v为列车运行速度;h为路基面中心以下深度。从式(7)、(8)可知列车速度影响系数为0.003,与高速铁路设计规范[18]中规定的速度影响系数基本一致。
由图7可知,由于轨道的不平顺性,路基动应力具有一定的变异性。在德国低干扰谱和京津城际轨道不平顺谱下和三种列车运行速度下,路基动应力变异系数沿深度方向都呈现逐渐衰减的趋势,且随着深度的加深,衰减速度逐渐加快。在同一种轨道不平顺谱下,列车速度越大,路基动应力的变异系数越大,从而说明列车速度对路基动应力的变异性具有放大效应。当列车速度相同时,在德国低干扰谱下的路基动应力的变异系数比京津城际轨道不平顺谱下的路基动应力的变异系数大,因此轨道不平顺性对路基动应力的变异性同样具有放大效应。另外,在德国低干扰谱下,当列车速度为350 km/h时,路基面动应力的变异系数约为0.17;而由武广线的现场实测结果统计可知[8],由于轨道不平顺性、列车速度变化、列车轴重变化等影响因素,路基面动应力的变异系数变化范围为0.15~0.3;对比可知轨道不平顺性是影响路基动应力变异性的最重要因素。因此,在路基设计中需特别注意轨道不平顺性的影响。
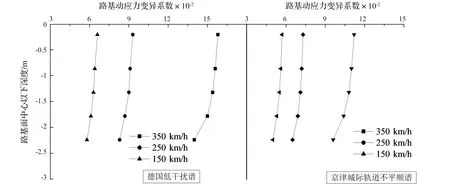
图7 路基动应力统计的变异系数Fig.7 COV of dynamic stressof subgrade
2.3路基动应力的概率分布形式
在得到路基动应力的均值和变异系数后,还需要确定路基动应力的概率分布型式。对数正态分布是很多参数近似服从的一种分布型式,且根据路基动应力的统计结果可以看出,路基动应力的概率分布型式接近于对数正态分布。对数正态分布概率密度函数f(x)及分布函数F(x)分别为:
(9)
(10)
式中:μ、σ分别是随机变量x的均值和标准差。
路基动应力的分布函数Fn(σd)可通过260个节点处的计算结果统计得到;并取对数正态分布函数F0(σd)的均值和标准差等于本文的计算统计结果。根据柯尔莫哥洛夫原理,取检验统计量:
(11)
式中:σdj为按递增顺序排列的第j个路基动应力计算值,1≤j≤260;根据分布函数的定义,路基动应力的分布函数Fn(σd)可由下式计算:
(12)
根据柯尔莫哥洛夫判断准则,取临界值Dn,α,当Dn 表3给出了在德国低干扰谱和京津城际轨道不平顺谱下,当列车分别以三种速度运行时路基面中心以下5个深度处Dn的统计结果。由表3可知,各深度处Dn的统计值均小于临界值Dn,α。图8给出了典型计算工况下路基动应力计算结果与对数正态分布预测曲线的对比图,发现两者非常接近。因此,可以认为在轨道不平顺下各深度处的路基动应力沿纵向均服从对数正态分布。 表3 路基动应力检验统计值 图8 路基动应力计算结果与对数正态分布预测曲线Fig.8 Calculation results and prediction curves of log-normal distribution for dynamic stress of subgrade 本文利用ABAQUS软件建立了列车-双轨道-双线路基有限元模型,在双线路基两股钢轨上添加了两种典型的轨道不平顺谱。根据计算结果,统计了不同列车速度下双线路基动应力的均值及变异系数沿深度方向的分布。最后,对双线路基动应力的概率分布形式进行了验证。得出以下结论: (1)在两种典型的轨道不平顺谱和三种列车速度下,路基动应力均值沿深度方向呈现直线衰减;路基动应力变异系数沿深度方向同样呈现衰减趋势,且随着深度增加,衰减速度逐渐加快。 (2)列车速度和轨道不平顺性对路基动应力的均值和变异系数均具有放大效应;当列车提速时,对轨道的不平顺性要求会显著提高。 (3)在轨道不平顺下,路基面中心以下各深度处路基动应力沿纵向均服从对数正态分布。 [1]刘升传,吴立坚,宋二详.动荷载路桥过渡段双线路基动力响应特性[J].交通运输工程学报,2009,9(6):26-32. LIU Shengchuan,WU Lijian,SONG Erxiang.Dynamic response properties of two-way subgrade in bridge-subgrade transition section under moving load[J].Journal of Traffic and Transportation Engineering,2009,9(6):26-32. [2]宗军良,刘涛,宫全美,等.既有线提速路基动力响应特性研究[J].中国铁道科学,2007,28(4):7-11. ZONG Junliang,LIU Tao,GONG Quanmei,et al.Dynamic response study on speed-increase subgrade of existing railway[J].China Railway Science,2007,28(4):7-11. [3]詹永祥,蒋光鲁.无砟轨道路基基床动力特性的研究[J].岩土力学,2010,31(2):392-396. ZHAN Yongxiang,JIANG Guanglu.Study of dynamic characteristics of soil subgrade bed for ballastless track[J].Rock and Soil Mechanics,2010,31(2):392-396. [4]董亮,赵成刚,蔡德钩,等.高速铁路无砟轨道路基动力特性数值模拟和试验研究[J].土木工程学报,2008,41(10):81-86. DONG Liang,ZHAO Chenggang,CAI Degou,et al.Experimental validation of a numerical model for prediction of the dynamic response of ballastless subgrade of high-speed railways[J].Chinese Civil Engineering Journal,2008,41(10):81-86. [5]陈雪华,律文田,王永和.高速铁路路桥过渡段路基动响应特性研究[J].振动与冲击,25(3):95-98. CHEN Xuehua,LÜ Wentian,WANG Yonghe.Study on the dynamic response of high speed railway bridge subgrade transition section[J].Journal of vibration and shock,25(3):95-98. [6]范生波.高速铁路路基动力响应测试分析[D].成都:西南交通大学,2010. [7]刘扬.有砟轨道沉降的概率预测模型[D].上海:同济大学,2007. [8]中铁第四勘察设计院集团有限公司.客运专线无碴轨道过渡段路基试验段动态响应测试研究分报告[R].武汉:中铁第四勘察设计院集团有限公司,2009. [9]程翀.车-轨-路耦合条件下的高速铁路板式轨道路基系统动力分析[D].杭州:浙江大学,2015. [10]LEI Xiaoyan,ZHANG Xing.Analysis of dynamic behavior for slab track of high-speed railway based on vehicle and track elements[J].Journal of Transportation Engineering,2011,137-227. [11]徐翔.高速铁路路基动力响应的现场测试及物理模型试验研究[D].杭州:浙江大学,2014. [12]常超.轨道不平顺引起的结构与地基振动[D].杭州:浙江大学,2012. [13]胡婷.列车移动荷载引起的路堤-地基振动与减振[D].杭州:浙江大学,2007. [14]刘学毅.客运专线无砟轨道设计理论与方法[M].成都:西南交通大学出版社,2010. [15]张斌,雷晓燕.基于车辆-轨道单位的无砟轨道动力特性有限元分析[J].铁道学报,2011,33(7):78-85. ZHANG Bin,LEI Xiaoyan.Analysis on dynamic behavior of ballastless track based on vehicle elements with finite element method[J].Journal of the China Railway Society,2011,33(7):78-85. [16]LIU G R,QUEK J S S.A non-reflecting boundary for analyzing wave propagation using the finite element method [J].Finite elements in analysis and design,2003,39(5):403-417. [17]翟婉明.车辆-轨道耦合动力学[M].北京:科学出版社,2007. [18]高速铁路设计规范(试行):TB 1062—2009[S].北京:中国铁道出版社,2010. Dynamic stress distribution of high-speed railway double-subgrade ZHANG Shiyou1,SUN Haijian1,CHEN Yanguo2 (1.Henan Electric Power Survey&Design Institute,Zhengzhou 45007,China;2.Yellow River Engineering Consulting Company,Zhengzhou 45003,China) Double-subgrade is one of widely used types of high-speed railway subgrades,to study its dynamic stress is very important.Here,a 3D finite element model of vehicle-track-double-subgrade was bulit using ABAQUS with two typical track irregularity spectra added on the two rails.Through numerical calculation,the dynamic stress distributions of subgrades in longitudinal direction were obtained under two typical track spectra and three train speeds.The mean values and the coefficients of variation (COVs)of subgrade dynamic stress under different depths of subgrade were statistically obtained,and the fitting formulas were deduced for the mean values.Using Kolmogorov rule,it was verified that the dynamic stress distribution of subgrades in longitudinal direction is approximately a log-normal distribution under track irregularity spectra. 3D finite element model of vehicle-track-double subgrade; track irregularity spectra; dynamic stress of subgrade; coefficient of variation(COV); log-normal distribution 2015-09-28修改稿收到日期:2016-02-22 张石友 男,高级工程师,1978年生 TU431 A DOI:10.13465/j.cnki.jvs.2016.17.028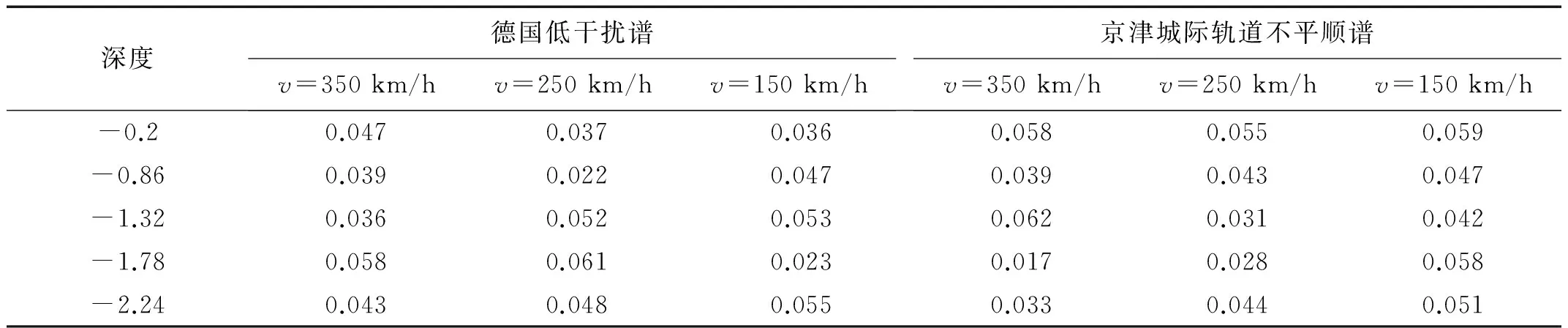

3 结 论

