低采样率下经验模态分解性能提升研究
黎 恒,李 智,莫 玮
(1.西安电子科技大学 机电工程学院,西安 710071; 2.桂林航天工业学院 自动化系,桂林 541004; 3.桂林电子科技大学 电子工程与自动化学院,桂林 541004)
低采样率下经验模态分解性能提升研究
黎恒1,李智2,3,莫玮1
(1.西安电子科技大学 机电工程学院,西安710071; 2.桂林航天工业学院 自动化系,桂林541004; 3.桂林电子科技大学 电子工程与自动化学院,桂林541004)
经验模态分解(EMD)使用信号极值点的位置和取值信息进行分解,对采样率有较高的要求。针对EMD在低采样率下性能降低的现象,提出一种基于B样条拟合的信号局部均值计算方法。首先提取信号极值点出现的时刻作为尺度,然后通过对极值点时刻进行重新采样构造B样条节点,最后应用B样条最小二乘拟合方法直接计算局部均值。与EMD方法相比,该方法不需要信号极值点的准确位置和取值,因此不容易受到低采样率的影响。对平稳信号和非平稳信号的仿真结果表明,该方法能在接近奈奎斯特频率的低采样率下获得较高的性能。与基于插值的解决方案相比,该方法的分离性能更好。
经验模态分解;B样条拟合;低采样率;信号分解;时频分析
希尔伯特-黄(HHT)变换[1]作为一种时间-频率分析方法,已经成为一种分析非线性和非平稳信号的标准方法。HHT的核心是经验模态分解(EMD)。通过EMD将输入信号分解成为一系列单模态分量,这些分量被称为本征模态函数(IMF)。在HHT中,对IMF进行希尔伯特变换即得到对应的时间-频率-幅度分布。与小波变换等方法不同,EMD方法不需要定义任何基函数,具有很强的自适应性。因此EMD在振动分析、机械系统、故障检测等领域得到了广泛的应用[2-7]。尽管如此,EMD方法也存在若干需要解决的问题,如低采样率误差[8]、模态混叠[9]和边缘效应[10]等。EMD方法的基本原理是通过一种筛分算法,不断地从输入信号中去除均值分量,从而得到关于时间轴对称的IMF。在筛分过程中,算法使用信号的极大值和极小值点产生均值曲线。因此,信号极值点的计算十分重要。在实际应用中,信号采样率会受到设备和实验条件的限制,往往不可能远大于信号的奈奎斯特频率。当采样率较低时,极值点的位置和取值将会出现误差,这些误差直接影响着均值曲线的精度,进而影响分解结果的精度。
针对这个问题,现有改进方法主要专注于对信号进行插值,然后对极值点进行定位。文献[11-12]给出基于sinc插值的重构方法,对信号进行插值,再进行EMD分解。文献[13]对信号包络使用升余弦插值,提高信号的等效采样率。这些方法在一定程度上提升了EMD在低采样率的性能。但是,sinc插值和升余弦插值做插值计算时收敛慢,需要较多的采样点,并且存在严重的边界失真;另一方面,这些方法对线性信号有很好的效果,而对非平稳信号可能产生额外误差;再者,对间断信号插值时通常会产生震荡,表现为较大的上冲或下冲,为接下来的EMD分解带来困难;最后,在采样率接近信号的奈奎斯特频率时,往往存在较大的误差。文献[14]使用二代小波插值对信号极值点进行定位,提高了极值点预测的精度。这些基于插值的方法对极值点位置和取值信息恢复的精度依赖性较强,并且其分解性能往往受限于EMD本身的精度。
由于目前基于插值的EMD改进方法存在上述弊端,本文提出一种基于B样条拟合的均值计算方法。该方法根据输入信号的极值点分布情况进行节点选取并通过拟合得到局部均值。由于不需要对信号插值进行极值点定位,因此该方法不存在极值点定位不准确带来的误差。本工作首先研究采样率对EMD方法的影响,然后针对这一问题提出基于B样条拟合的改进算法,并给出实现的原理和步骤,最后通过仿真实验来验证该方法的有效性和优越性。
1 采样率对EMD分解结果的影响
EMD方法以信号的极值点为特征,将输入信号分解成一组包络关于时间轴对称的IMF分量[1]。EMD计算步骤中的均值信号通过求其上下包络曲线的均值得到。由于上下包络曲线是通过对信号的极值点进行插值得到的,极值点的准确性直接影响着分解性能。随着采样率的降低,极值点的位置和取值将会偏离真实情况。文献[8]深入研究了采样率对EMD分解性能的影响并给出相关理论推导,这里不再赘述。为直观理解,给出实验进行说明。考察由10 Hz和3 Hz频率组成的双音信号s(t)=cos(2π×10t)+cos(2π×3t)。分别使用高采样率f1=1 000 sps和低采样率f2=25 sps对其进行采样得到离散时间序列,然后进行EMD分解。分解结果中第一阶IMF对应着频率较高的信号分量,即cos(2π×10t)。该分量的比较结果如图1(a)和图1(b)所示,可以明显看出采样率对分解结果有明显的影响。图1(c)为低采样率下高频信号分量,对应着预期准确的分解结果。通过对比可以直观地看出图1(b)和图1(c)有明显的不同,说明在低采样率下EMD分解带来了较大的误差。造成该现象的原因是在低采样率下,极值点的出现时刻和取值出现了波动,导致上/下包络出现了变化。为进一步说明低采样率带来的分解误差,考虑输入信号x(t)=cos(2π×10t)+cos(2π×10ft)。f为频率比,当f<1时cos(2πft)对应着低频信号分量。在不同采样率下对x(t)进行EMD分解,并计算分解结果第一阶IMF与真实结果的均方误差。实验中f取0.1~0.4,即对频率比不同的四组双音信号进行分解。采样率范围设置为25~1 000 sps。图2为均方误差对采样率的变化曲线。从图中可以得到以下结论。首先在低采样率下,特别是采样率小于100 sps时(或采样率/信号频率<10),分解结果有较大误差。其次,不同频率比的双音信号具有相似的误差曲线。最后,当采样率/信号频率>10时,分解结果的误差趋于平缓。通过该实验可以得到一个经验法则,即采样率应至少取有用信号频率的10倍才能保证分解精度。
下面从另一个角度说明EMD在低采样率下导致的问题,即在低采样率下IMF定义存在的问题。由于希尔伯特变换只能处理窄带信号,需要先对输入信号进行分解。EMD分解即是将输入信号分解成一系列局部窄带分量的方法。HUANG[1]认为单模态信号应与窄带信号的特征类似,其包络是关于时间轴对称的。然而他忽略了一个重要的事实,在低采样率下单模态信号的包络不一定关于时间轴对称(图1(c))。EMD方法强制要求IMF包络的对称性,在低采样率下将不可避免地产生误差。因此在这种情况下,使用信号上下包络产生均值是不恰当的。
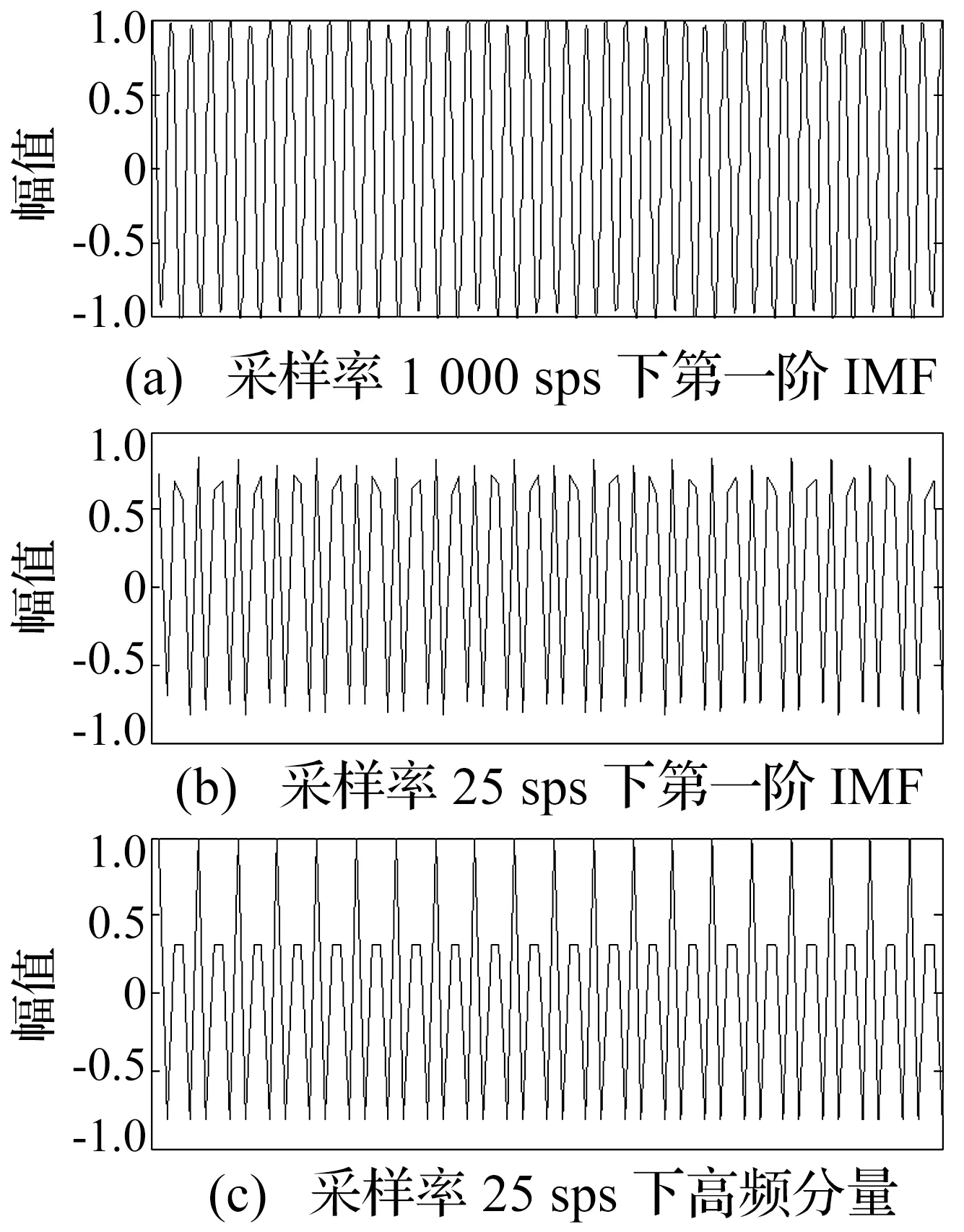
图1 不同采样率下EMD分解结果Fig.1 Decomposition under different sampling rates
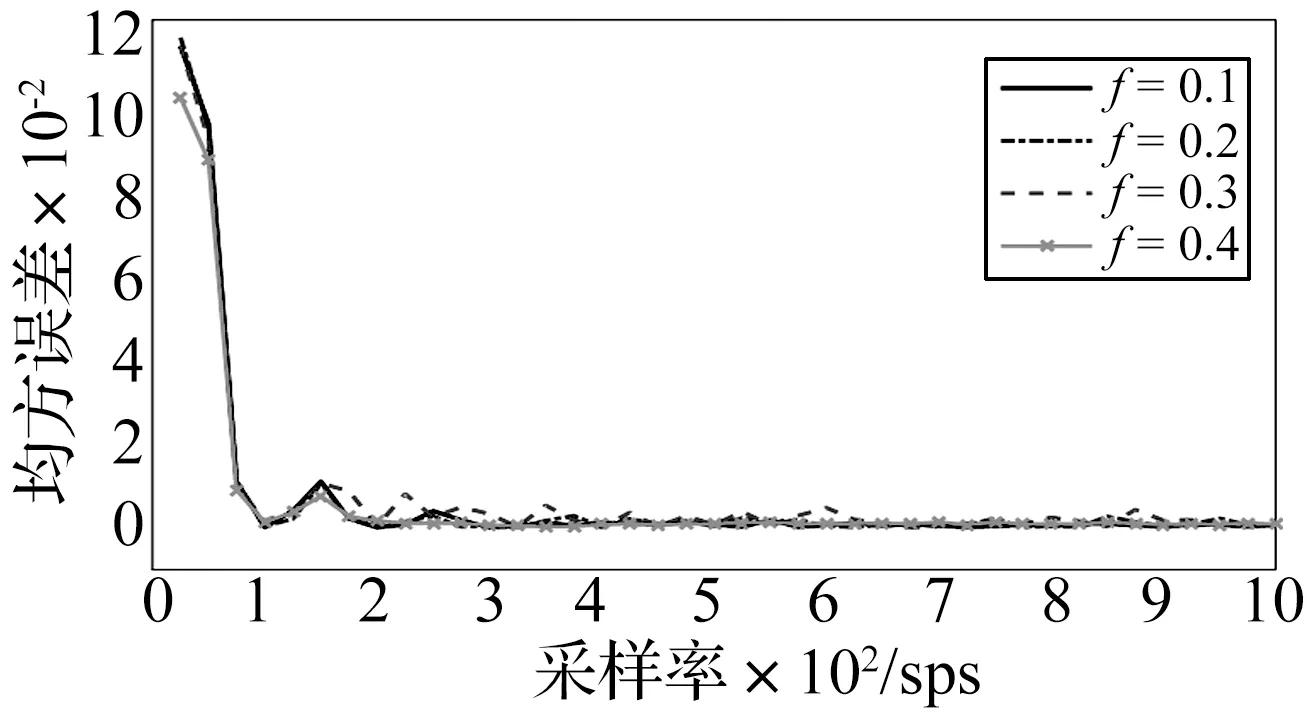
图2 不同采样率下分解第一阶结果与真实值的均方误差Fig.2 Mean squared error of the first IMF under various sampling rates
2 基于B样条拟合的均值计算方法
B样条是信号分析的重要工具,其计算方法包括B样条插值、B样条拟合和平滑B样条等。一些学者使用B样条对EMD进行了改进。文献[15]使用极值点的值做二项平均作为B样条控制系数进行均值计算,文献[16]使用平滑B样条生成上/下包络。与传统EMD方法类似,这些方法都使用了极值点的位置和取值,在低采样率下性能会受到影响。与已有方法不同,本文方法利用B样条拟合的低通滤波器性质,能很好地抑制低采样率导致的分解性能降低。
2.1B样条拟合
定义域[a,b]内的p阶B样条拟合的曲线g(t)表示为:
(1)
式中:cj为待求解的控制系数,Bj,p为p阶B样条函数。对[a,b]内给定的非递减节点u={u0,u1,u2,…,un+p},Bj,p使用Cox-de Boor递归公式计算[16]:
(2)
(3)
当p>1时,式(3)的分子和分母中都存在节点,因此Bj,p(t)乃至g(t)是关于节点的非线性函数。对输入信号y(t)进行B样条拟合可以表示为:
y(t)=g(t)+ε(t)
(4)
式中:ε(t)为拟合误差。B样条拟合就是求解关于控制系数cj的最小二乘问题。即求出cj,使Q最小
(5)
B样条是非线性函数,同时也是拟合非线性和非平稳信号的重要工具[16]。研究表明[17],B样条拟合具有低通滤波器的性质。滤波器的局部截止频率约为1/2m,其中fs为信号的采样频率,m为节点的局部距离。以等间隔节点为例,当节点间隔为2时,B样条拟合相当于截至频率为1/4的滤波器;节点间隔为1.5时,B样条拟合相当于截至频率为1/3的滤波器。该研究还指出,B样条阶数p趋向于正无穷时,该滤波器趋近于理想低通滤波器。
2.2算法实现
EMD方法认为,极值点的分布包含信号局部尺度信息。研究表明,当信号中高频模态幅度较明显时,极值点的分布往往和该高频模态分量的尺度一致[17]。通过前面分析可知,B样条拟合有滤波器的性质,其截至频率可控。在信号分解中,均值信号通常是频率较低的分量。因此,将极值点分布特征和B样条拟合相结合,可以计算出均值信号。本文方法的实质是使用B样条拟合滤波器实现高频分量和低频分量的分离。其基本步骤是:使用信号极值点出现时刻作为初始特征,然后对这些时刻进行重新采样得到时间分布密度较低的节点,最后使用该节点进行B样条拟合得到均值。本文关于均值信号的计算方法按照如下步骤进行:
(1)找出y(t)所有极值点出现的时刻,记为vi,i=1,2,3,…;
(2)在每个vi和vi+1之间以(vi+1-vi)/10为步长等间隔插入新的时刻,得到的序列记为ri,i=1,2,3,…;
(3)以k>10(本文取14)作为间隔对ri进行采样,得到的序列记为si,i=1,2,3,…;
(4)使用si作为节点进行p阶(本文取p=14)B样条拟合,并将拟合曲线作为均值曲线m(t);
计算出均值曲线后,剩下的处理步骤和EMD方法一致。步骤(3)中,k的取值决定了ri较vi的“稀疏”程度。以极值点等间隔的单音信号为例,设vi的时间间隔为τ,通过计算得到ri的时间间隔为τk/10。在这种情况下,以ri作为节点的B样条滤波器截至频率为10/2kτ。注意到该单音信号的频率为1/2τ>10/2kτ,因此当k>10时,B样条滤波器可以滤除该单音信号,得到频率较低的均值分量。在低采样率下,极值点出现时刻会出现微小波动,但是这些微小波动并不会引起si间隔的显著变化,因此不会引起B样条拟合滤波器截至频率的显著变化。
3 仿真实验
由于实际信号往往存在噪音、失真等现象,会对分解结果带来额外的影响,不利于性能评价。本文使用仿真信号来进行分析算法在低采样率下的性能,包括平稳信号和非平稳信号。
3.1平稳信号的分离性能
本小节研究本文方法对平稳信号分解性能。考虑下面的双音信号模型:
x(t;a,f)=cos2πt+acos(2πft+φ)
(6)
式中:a为幅度比,f为频率比,φ为相位差。当f∈(0,1)时,式(6)中第一项为高频分量,第二项为低频分量。由EMD方法的分解原理可知,先分解出来的IMF为频率较高的分量。为评价分解性能,考察第一阶IMF与高频分量的相似度,使用文献中常用的公式作为评判标准[18]:
(7)

图3 不同采样率下分离性能比较Fig.3 Comparison of separation quantity between EMD and the proposed method under different sampling rates
当分解出的IMF与高频分量完全相同时,式(7)为零。定义一个阈值,当c(a,f,φ)<0.5时认为分解是成功的。相位差φ通常被认为对分解结果影响不大,本文随机取5个相位分解结果的平均作为输出。图3给出了EMD和本文方法在不同采样率fs下的分解结果。图中黑色部分为分解成功的区域,白色部分为分解失败的区域。图3(a)和图3(b)给出EMD方法在采样率fs=5fN和fs=1.5fN下的分解结果,其中fN为高频分量的奈奎斯特频率。从分解结果看,采样频率对EMD分离性能有较大影响。当采样率降低时,代表分解成功的黑色区域面积明显减小。图3(c)和图3(d)给出了本文方法fs=1.5fN和fs=1.1fN下的分解结果。与EMD方法相比,本文方法成功分解的区域面积更大。随着采样率的进一步降低,当fs=1.1fN接近奈奎斯特频率时,本文方法的分解性能并未出现明显下降。这些实验结果充分验证了本文方法性能在低采样率下的稳定性和优越性。
值得注意的是,本文方法中,k的取值对频率分离性能有直接影响。回顾本文算法,k=14的情况下,B样条拟合滤波器的截至频率约为0.35τ=0.7×0.5τ。因此该算法能分离频率比f=0.7的信号分量。同理可以得到,当k=12时,f=0.8,当k=11时,f=0.9。图3(e)给出了分解结果中分解成功/失败过渡区域的轮廓曲线,即对应C(a,f)=0.5的曲线。使用三组不同的配置以考察频率分辨率并在结果中使用不同的线条表示:k=11用虚线,k=12用实线,k=14用短划线。图中还给出EMD分解结果,用点虚线表示。可以看出,参数k直接决定着SAMD的分解的频率分辨率,其性能与理论预期一致。
3.2非平稳信号的分离性能
使用FM信号作为非平稳信号的例子来评价本文方法的分解性能。
y(t)=cos(2πft+0.12πft×cos2πt)+
acos(πft+0.06πft×sin2πt)
(8)
式中:t∈[0,1],FM信号的中心频率为f=1.5fN。对该信号分别使用EMD、基于sinc插值EMD和本文方法进行分解。为直观地观察分解性能,对分解结果求希尔伯特谱。EMD分解结果如图4(a)所示,可以很明显地看到低采样率对EMD分解的影响。希尔伯特谱出现了严重的失真,甚至在低频段出现了多余的杂散分量。图4(b)给出了基于sinc插值重构的分解结果。从分解结果看,插值确实带来了性能的提升,但仍存在明显的失真和边界问题。本文方法分解结果如图4(c)所示。可以看出,高频和低频分量的时频分布清晰可辨,失真低,说明本文方法更好地实现了信号的分离。

图4 分解结果的希尔伯特谱Fig.4 Comparison of Hilbert spectra
3.3精度
选取双音信号的分解精度进行考察,比较EMD、二代小波插值[14]和本文方法的性能。本小节实验的配置与第一章中演示实验类似,考虑输入信号x(t)=cos(2π×10t)+cos(2π×10ft)。在不同采样率下对x(t)进行EMD分解,并计算分解结果第一阶IMF与真实结果的均方误差。实验中f取0.1到0.4,采样率范围设置为25~1 000 sps。对不同双音信号分解得到的结果进行算术平均并取对数,实验结果如图5所示。首先比较采样率为25 sps到100 sps的分解性能。与EMD相比,基于二代小波插值的方法在该区域的分解精度得到明显提升,其中当采样率为25 sps时精度提升了1个数量级。本文方法获得的精度提升更为明显,当采样率为25 sps时精度提升了约1.5个数量级。下面比较100 sps到1 000 sps的分解精度。在该区域插值已无法带来精度的提升,这是因为插值对极值点位置预测的改善已经很微小,另一方面插值方法带来的精度提升受限于EMD本身的分解精度。为比较B样条阶数p对分解精度的影响,本文方法分别使用p=14和p=10两种阶数进行分解对比。可以看到本文方法在整个采样率范围都可以带来分解性能的提升。另一方面,提高B样条阶数p能提升分解精度。这是因为p取值越大B样条滤波器的滚降越大,越接近理想低通滤波器。然而当p的取值过大时,会使式(5)的求解变得更复杂。因此增大p带来的性能提高是以更多计算时间为代价的。如本文取p=14时,能带来较明显的精度改善,计算时间约为EMD方法的4倍。
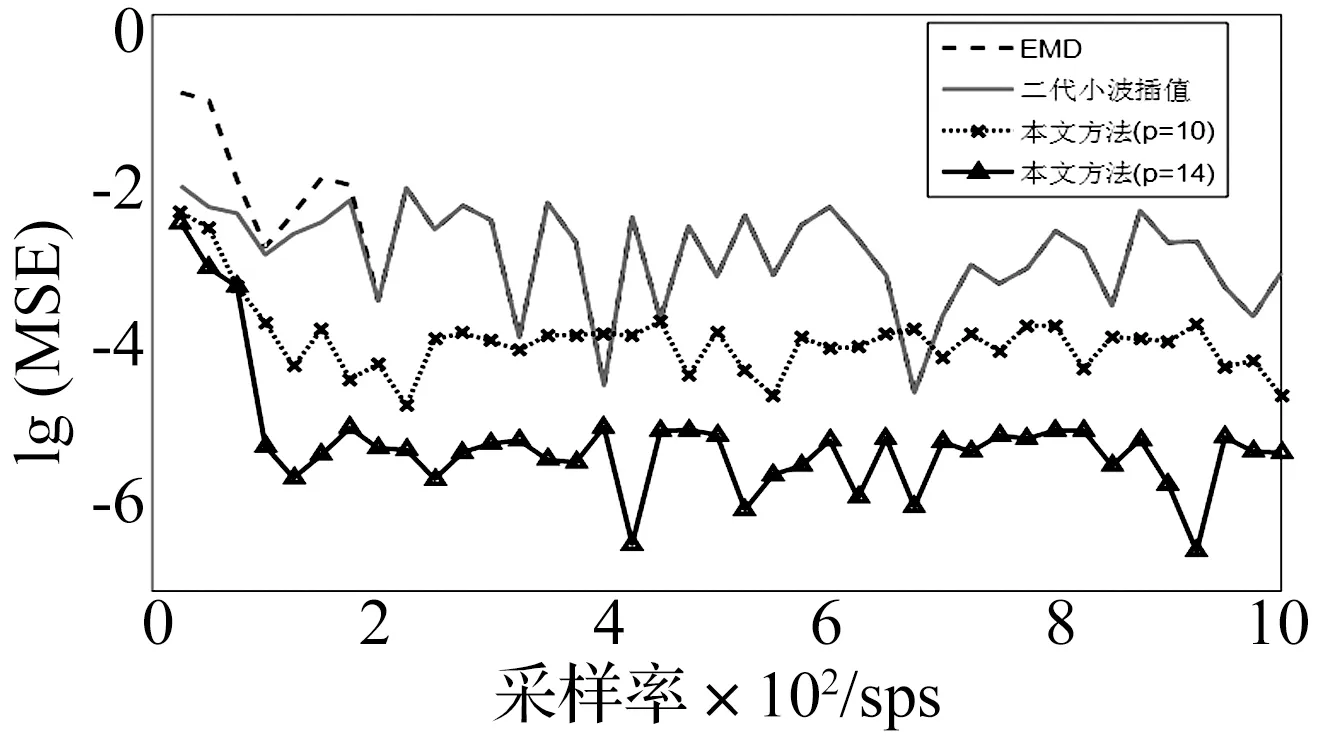
图5 不同采样率下分解精度比较Fig.5 Comparison of accuracy under various sampling rates
4 结 论
本文针对低采样率下EMD存在的分解不准确的问题,提出一种基于B样条拟合的均值计算方法。仿真实验表明通过本文方法能有效地消除低采样率带来的影响。本文方法与现有方法的不同之处在于:
(1)该方法的控制系数通过最小二乘方式确定,直接计算均值信号,不需要计算上/包络。
(2)不需要知道极值点的准确位置或准确取值。该方法只需要知道信号极值点大致出现的时刻。因此,该方法对低采样率有很好的适应性。但是该方法目前尚不能解决模态混叠问题,在今后的工作中,如何抑制模态混叠是重点研究内容。
[1]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London.Series A,1998,454(1971):903-995.
[2]吴响,钱建生,王海燕.微震信号多尺度非线性特征提取与辨识研究[J].仪器仪表学报,2014,35(5):969-975.
WU Xiang,QIAN Jiansheng,WANG Haiyan.Study on multi-scale nonlinear feature extraction and signal identification for microseismic signal[J].Chinese Journal of Scientific Instrument,2014,35(5):969-975.
[3]王录雁,王强,张梅军,等.基于 EMD 的滚动轴承故障灰色诊断方法[J].振动与冲击,2014,33(3):197-202.
WANG Luyan,WANG Qiang,ZHANG Meijun,et al.A grey fault diagnosis method for rolling bearing based on EMD [J].Journal of Vibration and Shock,2014,33(3):197-202.
[4]YANG Z,LING B W K,BINGHAM C.Trend extraction based on separations of consecutive empirical mode decomposition components in Hilbert marginal spectrum[J].Measurement,2013,46(8):2481-2491.
[5]KOMATY A,BOUDRAA A O,AUGIER B,et al.EMD-based filtering using similarity measure between probability density functions of IMFs[J].IEEE Transactions on Instrumentation and Measurement,2014,63(1):27-34.
[6]GOHARRIZI A Y,SEPEHRI N.Internal leakage detection in hydraulic actuators using empirical mode decomposition and hilbert spectrum[J].IEEE Transactions on Instrumentation and Measurement,2012,61(2):368-378.
[7]LEI Y,LIN J,HE Z,et al.A review on empirical mode decomposition in fault diagnosis of rotating machinery[J].Mechanical Systems and Signal Processing,2013,35(1):108-126.
[8]RILLING G,FLANDRIN P.On the influence of sampling on the empirical mode decomposition[C]// IEEE International Conference on Acoustics,Speech and Signal Processing.Toulouse:IEEE,2006:444-447.
[9]肖瑛,殷福亮.解相关 EMD:消除模态混叠的新方法[J].振动与冲击,2015,34(4):25-29.
XIAO Ying,YIN Fuliang.Decorrelation emd:a new method of eliminating mode mixing[J].Journal of Vibration and Shock,2015,34(4):25-29.
[10]王录雁,王强,鲁冬林,等.EMD自适应三角波匹配延拓算法[J].振动与冲击,2014,33(4):94-99.
WANG Luyan,WANG Qiang,LU Donglin,et al.A self-adaptive triangular waveform matching extension algorithm for EMD[J].Journal of Vibration and Shock,2014,33(4):94-99.
[11]XU Z,HUANG B,ZHANG F.Improvement of empirical mode decomposition under low sampling rate[J].Signal Processing,2009,89(11):2296-2303.
[12]ROY A,DOHERTY J F.Improved signal analysis performance at low sampling rates using raised cosine empirical mode decomposition[J].Electronics Letters,2010,46(2):176-177.
[13]CHEN Q,HUANG N,RIEMENSCHNEIDER S,et al.A B-spline approach for empirical mode decompositions[J].Advances in Computational Mathematics,2006,24(1/2/3/4):171-195.
[14]赵利强 王建林 于涛.基于改进EMD的输油管道泄漏信号 特征提取方法研究[J].仪器仪表学报,2013,34(12):2696-2702.
ZHAO Liqiang,WANG Jianlin,YU Tao.Study on the extraction method for oil pipeline leakage signal feature based on improved empirical mode decompositio [J].Chinese Journal of Scientific Instrument,2013,34(12):2696-2702.
[15]KIM D,PARK M,OH H S.Bidimensional statistical empirical mode decomposition[J].Signal Processing Letters,IEEE,2012,19(4):191-194.
[16]UNSER M,ALDROUBI A,EDEN M.B-spline signal processing.I.Theory[J].IEEE Transactions on Signal Processing,1993,41(2):821-833.
[17]UNSER M.Splines:A perfect fit for signal and image processing[J].IEEE Signal Processing Magazine,1999,16(6):22-38.
[18]RILLING G,FLANDRIN P.One or two frequencies? The empirical mode decomposition answers[J].IEEE Transactions on Signal Processing,2008,56(1):85-95.
Performance improvement of EMD under low sampling rates
LI Heng1,LI Zhi2,3,MO Wei1
(1.School of Mechano-Electronic Engineering,Xidian University,Xi’an 710071,China;2.Guilin University of Aerospace Technology,Guilin 541004,China;3.School of Electronic Engineering and Automation,Guilin University of Electronic Technology,Guilin 541004,China)
Empirical mode decomposition (EMD)depends highly on exact locations and values of signal extrema,they need a higher sampling rate.Aiming at improving the performance of EMD under low sampling rates,a local mean estimation method based on B-spline fitting was proposed.Firstly,the occuring instant of extrema was extracted as a time scale.Then,the occuring instant of extrema was re-sampled to construct node points of B-spline.Finally,the local mean was computed directly with B-spline least squares method.Compared with EMD method,the proposed method did not need the exact locations and values of extrema,so the low sampling rates were not easy to affect this technique.The efficiency of this technique was demonstrated using simulated signals.The simulation results showed that the performance of the proposed method is not reduced even the sampling rate is close to Nyquist rate; the proposed method is superior to existing interpolation methods in separation performance.
empirical mode decomposition (EMD); B-spline fitting; low sampling rates; signal decomposition; time-frequency analysis
国家自然科学基金(61361006)
2015-04-07修改稿收到日期:2015-09-16
黎恒 男,博士生,1982年4月生
李智 男,博士,教授,1965年5月生
TH137
A DOI:10.13465/j.cnki.jvs.2016.17.031

