筒壁沟槽式制退机主流液压阻力系数分析
潘孝斌,宋彦明,谈乐斌
(1.南京理工大学 机械工程学院,南京 210094;2.内蒙古北方重工集团有限公司 科研院,内蒙古包头 014033)
筒壁沟槽式制退机主流液压阻力系数分析
潘孝斌1,宋彦明2,谈乐斌1
(1.南京理工大学 机械工程学院,南京210094;2.内蒙古北方重工集团有限公司 科研院,内蒙古包头014033)
液压阻力系数k1是反映主流流道结构特征的参数,是火炮制退机设计的关键,相似流道结构特征时可参考取值,而不同流道结构时取值范围相差较大。针对某筒壁沟槽式制退机,为了确定合理的k1取值范围,对其影响参数、变化规律进行了研究。通过筒壁沟槽式制退机主流流道特征进行分析,经合理简化,将活塞杆固定,设定入口边界流速V′模拟制退杆后坐运动速度V,出口边界为自由流出,在Fluent软件中建立了主流流场等效分析模型,通过仿真得到活塞壁面受力大小,再由伯努利方程推导得到液压阻力系数k1,并以某成熟制退机为例进行了方法验证。按照该方法,研究了后坐速度V和流道截面积ax对k1的影响,其在后坐过程中是动态变化的,随着后坐速度、流道面积减小,在一定范围内逐渐增大。在所设计的制退机结构参数条件下,结合后坐阻力仿真与试验结果对比,k1合理的取值范围为2.4~2.7。
制退机;液压阻力系数;流场仿真;后坐阻力
反后坐装置是火炮的核心部件,发射过程中炮身上承受的巨大冲击力经反后坐装置缓冲后再作用在炮架上,从而缓解火炮威力和机动性之间的矛盾。其中,制退机是消耗后坐能量、控制平稳后坐的关重部件。制退机的结构形式主要有节制杆式、活塞沟槽式、筒壁沟槽式等结构形式,通过活塞挤压工作腔中的制退液流过孔口提供后坐阻力。节制杆式制退机因其结构简单、动作确实可靠,目前广泛应用于各类制式火炮中[1]。
在工程实践中,制退机液压阻力系数的选取对于制退机的理论计算和结构设计具有极其重要意义。对于新设计的制退机,通常根据经验按相似结构类比的方法确定,再结合试验进行反复修正,实际结果一般与初定值偏差不大,例如节制杆式的主流液压阻力系数k1在1.2~1.6范围内选取确定,支流液压阻力系数k2在4~6范围内选取。
但是,如果新设计的制退机不是采用节制杆结构形式,那么就不能完全参考上述提及的液压阻力系数选取范围。例如,国外某型制退机采用筒壁环形沟槽流动形式,工作腔液体通过活塞与筒壁间的环形间隙流过,其设计计算书上的主流系数取值约为2,若按节制杆式进行取值,势必造成制退机设计过程的理论分析与试验不符。
随着计算机技术和计算流体力学(CFD)的发展,数值模拟手段广泛应用于流体机械内部的复杂流动研究[2]。文献[3]将制退机的局部复杂结构适当简化,选定局部损失系数,建立液压阻力模型,以某152 mm加榴炮为例进行对比分析,该分析方法为设计新型火炮提供了参考。文献[4]采用动网格技术模拟火炮后坐时制退杆和活塞的运动,通过制退机内部三维流场数值模拟,较为精确地计算后坐液压阻力,为制退机设计和优化提供理论基础。文献[5]以某火炮制退机为研究对象,建立实际结构三维模型,分别采用标准k-ε模型、RNG k-ε模型和Realizable k-ε模型计算制退机内部各腔室压力并与试验对比,研究了湍流模型对制退机内流场计算的适应性,结果表明标准k-ε模型计算的误差最小。上述相关研究方法、湍流模型的选取都为后续研究起很好借鉴作用,本文针对新型设计的制退机如何选择合适的液压阻力系数以及在工程设计中的实践应用这一问题进行了深入研究。
1 筒壁沟槽式制退机
某型火炮考虑总体结构布置、炮架结构、火线高、射击稳定性等因素,总体设计要求结构布局紧凑、后坐相对较长,且对制退机轴线与身管轴线间距严格限制,导致外筒直径有所限制,若采用常规长后坐节制杆形式,节制杆的稳定性不能满足要求。经多方讨论,拟在制退筒内壁开启沟槽,制退杆后坐,工作腔中的制退液主要通过活塞与制退筒内壁均布的三个变截面沟槽流动,从而产生主流后坐阻力,筒壁沟槽式制退机总体结构如图1所示。
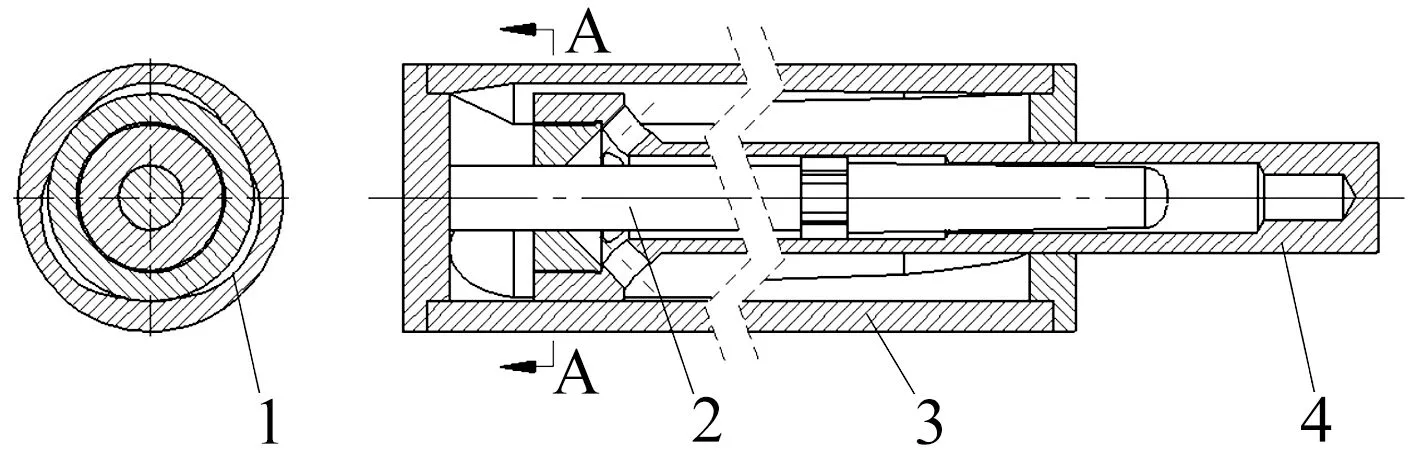
1.流液口 2.支撑杆 3.外筒 4.制退杆图1 筒壁沟槽式制退机结构简图Fig.1 Sketch of cylinder groove recoil mechanism
传统意义上的节制杆改为等直径的支撑杆,无液流通过,支流流动与常规节制杆式制退机相似,确保制退杆内腔充满液,在复进时起节制作用。其中,主流的流动与节制杆式结构相差较大,而且主流液压阻力系数k1值的确定对反后坐装置液压阻力计算影响较大,支流的流动则基本相似。
文献[1]中对制退机液压阻力分析和假设条件,并结合筒壁沟槽式制退机结构特点,推导得液压阻力方程为
Fφh=
(1)
式中,Fφh为制退机的液压阻力,k1、k2为主流、支流液压阻力系数,A0为活塞工作面积,Ap为支撑杆面积,ax为沟槽流道面积,Afj复进节制工作面积,A1为支流最小面积,ρ为制退液密度,V为制退杆后坐速度。
式(1)前项为主流提供的液压阻力,与常规节制杆式制退机液压阻力方程略有差别,后项为支流提供的液压阻力。可以看出,除了相关结构参数外,液压阻力系数对液压阻力的影响十分明显。
由于支流流动与节制杆式制退机相似,因此本文主要针对主流流动及其液压阻力系数k1进行分析。在此需要特别指出,主流液压阻力系数k1的取值是综合考虑各种液体流动损失、运动全过程的一个综合系数,而实际上它是根据流体速度、结构特征等参数在一定范围内变化的,通常是预先确定合理的取值范围,再根据试验结果反复进行参数修正方可确定。
2 主流流动简化模型
通过简化,活塞处于沟槽某截面积时的主流等效流动的模型如图2所示,将活塞和外筒固定,活塞周向均布三个流道,右侧制退液以一定速度V′流入,通过筒壁上的三个流液通道后在左侧自由流出。根据伯努利方程和简化假设条件,可得等效模型流动过程的液压阻力方程,如式(2)所示。

图2 主流等效流动模型示意图Fig.2 Sketch of mainstream equivalent model
(2)
图2中的简化模型是为了便于流场仿真分析,将活塞和筒壁边界固定,给定入流速度V′进行计算的,而实际工作过程为筒壁固定,杆后坐,只有当两种情况下的流道处绝对速度ω相同时,可认为简化模型的流场与实际工作过程等效。
因此,在实际运动中,推导可得杆后坐时沟槽流道绝对速度为
(3)
结合式(2)和式(3),可得实际制退杆后坐速度V与等效模型中制退液入流速度V′关系为
(4)
3 液压阻力系数分析方法验证
通常,不同结构形式的液压流动阻力系数需通过试验的方法进行确定,对模拟试验装置活塞进行拉伸,测得拉力和活塞速度后进行解算,试验成本高、耗时长。随着计算机仿真技术发展,流场数值仿真分析方法逐渐得到应用,并且具有较高的可信度,本文拟采用流场数值仿真方法对制退机主流流场进行分析,以获得液压阻力系数取值范围。
3.1基本控制方程
假设制退机内部液体进行不可压缩三维粘性流动,控制方程为连续性方程、动量方程和能量方程,各控制方程通用形式为[2]:
(5)
式中,ρ为密度,t为时间,u,v,ω分别为速度矢量在x,y,z轴方向上的分量,为通用变量;Γ为广义扩散系数,S为广义源项。对于特定的方程组φ、Γ、S都具有特定的形式,所有控制方程都可以经过适当处理,将方程中的因变量、时变量、对流项和扩散项写成通用形式,进而通过Fluent软件进行处理。
3.2分析方法验证
为验证通过流场仿真确定主流液压阻力系数k1范围的方法是可行的,文中先以较为成熟的某105 mm火炮节制杆式制退机进行流场分析。为后续描述方便,文中取名为制退机A,建立的主流液压阻力系数流场仿真模型如图3所示,由于轴向对称取1/2模型。主要结构参数:活塞直径125 mm,制退杆外径60 mm,节制杆局部直径28.2 mm,节制环内径38 mm,活塞位于后坐阶段前期,流道面积约509 mm2。
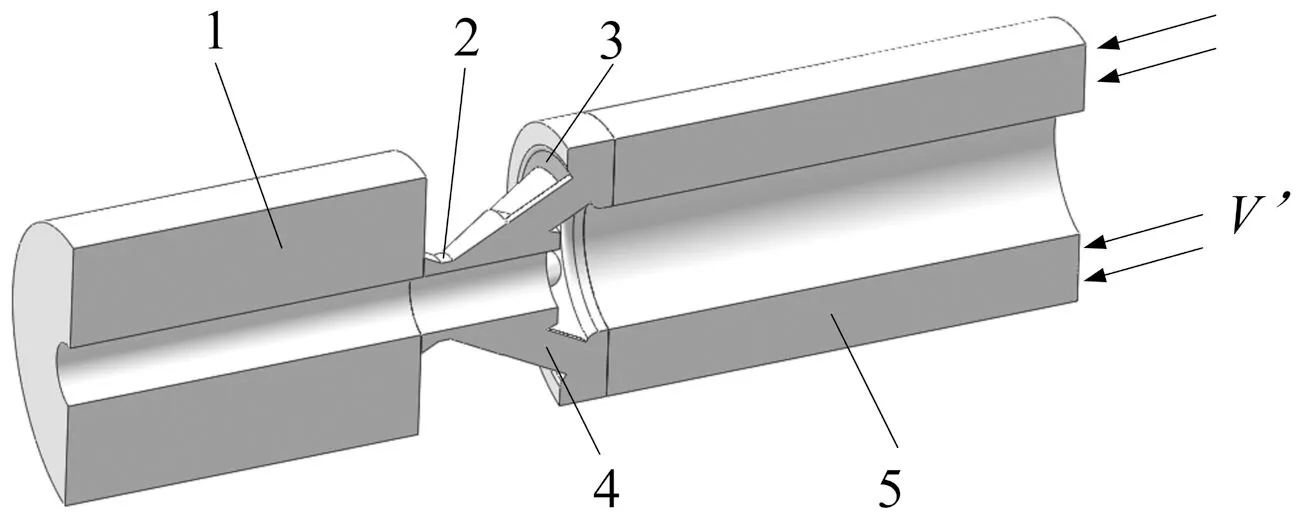
1.非工作腔 2.节制环位置 3.活塞壁面 4.液流通道 5.工作腔图3 制退机A流场计算模型Fig.3 Flow field model of recoil mechanism A

通过仿真,例如在入流速度V′=10 m/s时,得到制退机A对称面流场速度分布如图4所示,活塞面合力为110.3 kN。

图4 制退机A速度场Fig.4 Velocity field of recoil mechanism A
同样按上述计算方法,分别设定不同入流速度V′,2~12 m/s,间隔1 m/s,然后根据式(3)关系转换成后坐速度V与液压阻力系数k1的关系,拟合曲线如图5所示。
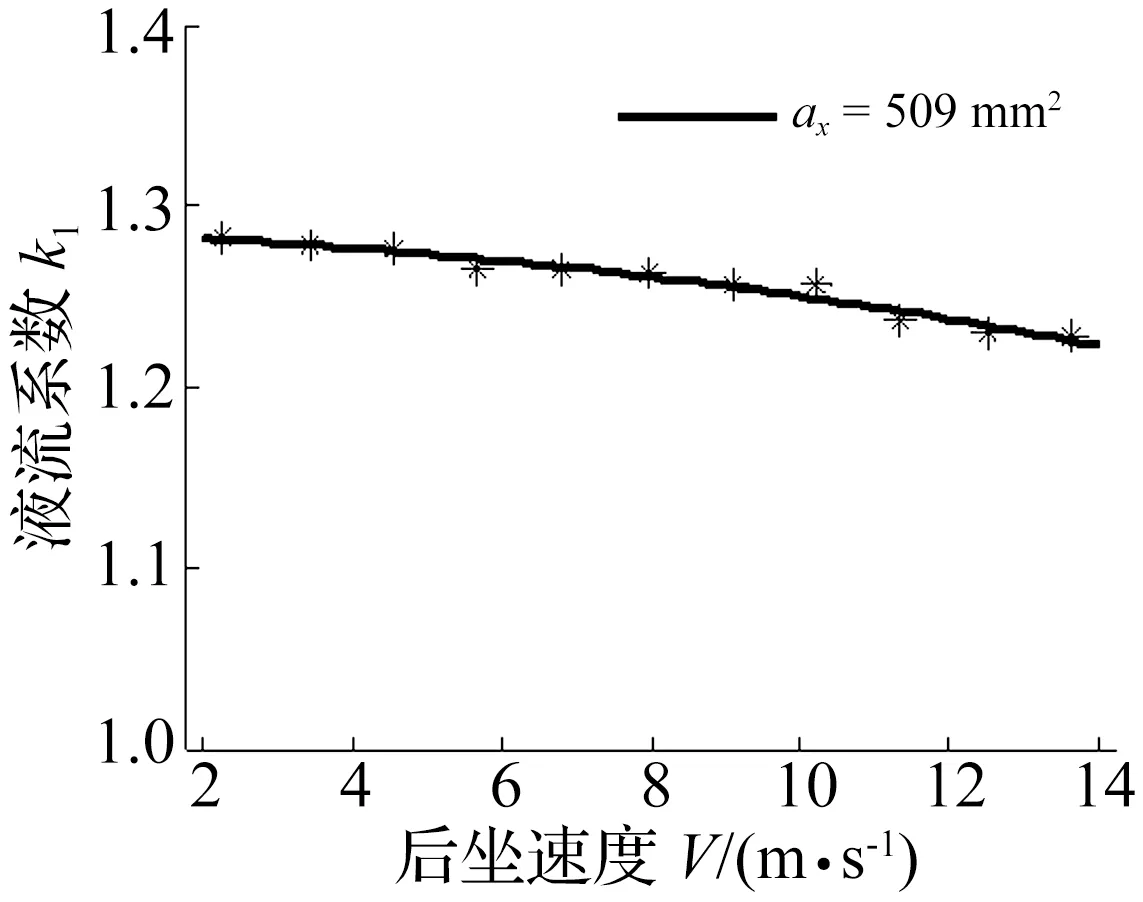
图5 制退机A系数k1与后坐速度V关系Fig.5 Relationship of k1 and V of recoil mechanism A
根据图5仿真结果,制退机A的液压阻力系数k1的理论取值范围为1.2~1.4,查阅产品设计计算书中的取值,k1=1.27,在此范围内,同时也符合文献[1]中提供的取值范围,说明在新型制退机初步设计阶段,通过流场仿真分析以此来确定主流液压阻力系数k1范围的方法是合理、可行的。
4 筒壁沟槽式主流系数分析
4.1入流速度和流道面积的影响
影响筒壁沟槽式制退机主流流场变化的主要参数为制退机的结构特征、尺寸和后坐运动速度,其中结构特征和尺寸是固定的,但是在后坐运动过程中,后坐速度也在不断变化的,同时,主流通道截面积是随着沟槽深度逐渐变化的,因此有必要分析上述两个变量对主流液压阻力系数k1的影响。为后续描述方便,文中对所研究的筒壁沟槽式制退机取名为制退机B。
根据初步设计的制退机B结构参数,经简化后建立的流场分析模型如图6所示,流道截面积可随结构参数变化在一定范围内调整,轴向对称取1/2模型,按节3.2中方法进行仿真分析。
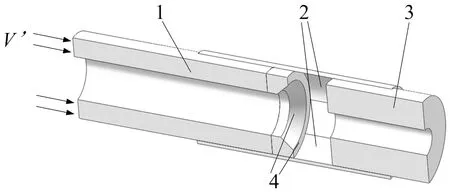
1.工作腔 2.筒壁沟槽 3.非工作腔 4.活塞壁面图6 制退机B流场计算模型Fig.6 Flow field model of recoil mechanism B
同样,通过设定不同的入流速度V′以模拟制退杆后坐速度V,同时改变流道截面积以反映不同后坐位置的情况,求得液压阻力系数k1值。通过仿真,例如在入流速度V′=8 m/s、ax=138 mm2时的流场速度分布如图7所示。

图7 制退机B速度场Fig.7 Velocity field of recoil mechanism B
对入流速度1~12 m/s,间隔1 m/s,液流通道面积取460 mm2,282 mm2和138 mm2,代表后坐时活塞在工作前段、中段和末段位置,分别设定流场模型参数进行了仿真计算,根据式(2)求得液压阻力系数k1值,根据式(3)转换成后坐速度关系,拟合结果如图8所示。
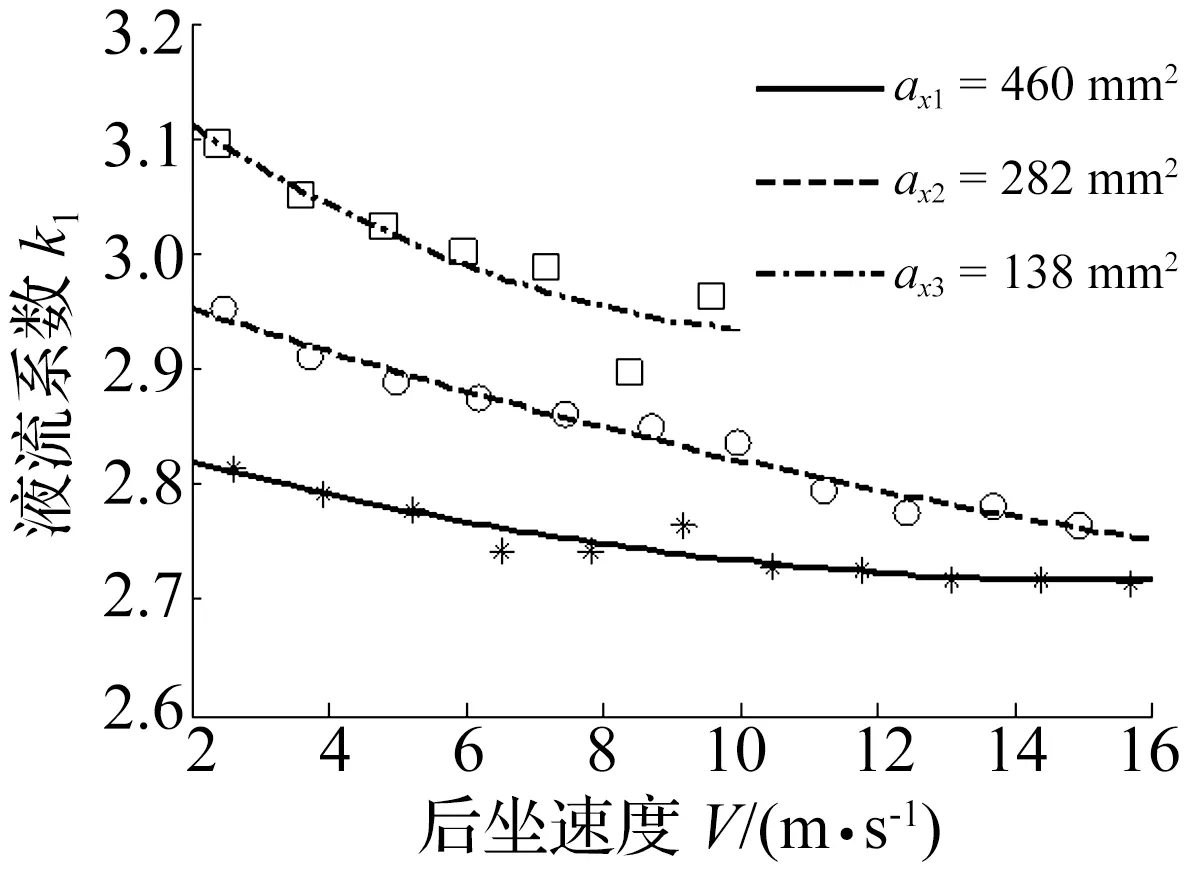
图8 制退机B系数k1与后坐速度V关系Fig.9 Relationship of k1 and V of recoil mechanism A
图8仿真结果表明,随着筒壁沟槽流通面积ax减小,k1值增加,并且随着后坐速度下降,k1值也略有上升。制退机B主流液压阻力系数k1的理论取值范围为2.7~3.1,确实与节制杆式参考的取值范围1.2~1.6相差较大,这是由两者的流场结构特征决定的,局部流动损失越大,液压阻力系数越高。仿真研究结果为新设计的筒壁沟槽式制退机液压阻力系数k1初值设定提供了必要参考依据。
4.2加工间隙的影响
5 液压阻力系数应用及验证
依据上述分析得到的主流液压阻力系数选取范围,在工程实践中指导设计人员对筒壁沟槽式制退机进行正面设计,在活塞直径、制退杆直径、极限后坐长、最大后坐阻力大致确定的条件下,对沟槽流道面积进行调整,然后再进行反面计算。根据火炮后坐运动分析中的动力学方程组,涉及制退机力、复进机力、摩擦阻力、射角等因素,在MatlabSimulink仿真环境下建立火炮后坐运动仿真模型,将内弹道数据、设计结构参数带入求解[8-10],并通过多次正面与反面设计交替,最终确定具体结构参数,进行了加工制造、调试和靶场试验。
通过试验数据对比,当液压阻力系数k1取值为2.5时,仿真计算得到的制退机后坐阻力与试验结果较为吻合,该取值也符合节4.2的分析结果,两者对比如图9所示。
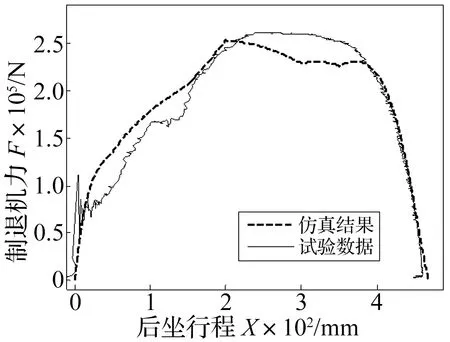
图9 制退机B后坐力试验与仿真对比Fig.9 Recoil force comparison of test and simulation
由图9分析可知,制退机B后坐阻力仿真结果与试验值在变化趋势上是一致的,最大后坐阻力仿真值为253 kN,试验值为262 kN,误差3.4%;最大后坐位移仿真值为468 mm,试验值为460 mm,误差0.17%。
由于后坐运动仿真模型计算中系数k1取固定值,在后坐行程前段,制退机力仿真结果高于试验值,说明系数k1取值偏大;而在后坐行程中后段,仿真值低于试验值,说明k1取值偏小,因此系数k1在后坐运动中是在一定范围内动态变化的,呈现出前低后高的特点,同时也验证了图8所得的系数k1变化规律,随着后坐速度、流道面积减小,系数k1取值越大。然而在工程上为方便计算,通常取固定值,结合本文制退机结构特点、加工工艺和试验对比结果,认为系数k1合理的取值范围为2.4~2.7,这为今后工程上相类似制退机结构设计提供参考。
6 结 论
(1)主流液压阻力系数k1是反映流道特征的参数,是制退机工程设计的关键,不同结构形式的制退机系数k1取值偏差较大,节制杆式制退机采用结构相似类比方法可获得相近结果,其它结构形式的制退机在设计前期选取系数k1时,有必要通过试验或流场分析方法确定合理范围;
(2)文中通过主流等效流动模型的简化,采用流场仿真分析方法,根据伯努利方程来确定主流液压阻力系数k1取值范围的方法是合理、可行的;
(3)工程上为简化计算,制退机主流液压阻力系数k1通常取固定值,但其实际上是在一定范围内变化的,随着后坐速度、流道面积减小,系数k1逐渐增大;
(4)针对文中设计的筒壁沟槽式制退机,主流液压阻力系数k1理论上取值范围为2.7~3.1,实际考虑到活塞与内筒臂间隙,以及筒壁沟槽加工误差因素,并结合与试验结果对比,k1合理的取值范围应为2.4~2.7,为相类似结构的制退机设计提供参考依据。
[1]高树兹,陈运生,张月林,等.火炮反后坐装置设计[M].北京:兵器工业出版社,1995.
[2]王福军.计算流体动力学分析-CFD软件原理与应用[M].北京:清华大学出版社,2004.
[3]赵建新,王兴贵,张鸿浩.基于局部损失的制退机液压阻力模型[J].兵工学报,2001,22(4):441-443.
ZHAO Jianxin,WANG Xinggui,ZHANG Honghao.A hydraulic resistance model for recoil brake based on local losses[J].Acta Armamentarii,2001,22(4):441-443.
[4]范永,刘树华,曹广群.基于动网格的某制退机三维流场数值模拟与分析[J].火炮发射与控制学报,2010(4):63-65.
FAN Yong,LIU Shuhua,CAO Guangqun.Numerical simulation and analysis on 3D flow field of a recoil mechanism based on dynamic mesh[J].Journal of Gun Launch & Control,2010(4):63-65.
[5]张晓东,张培林,傅建平,等.k-ε双方程湍流模型对制退机内流场计算的适用性分析[J].爆炸与冲击,2011,31(5):516-520.
ZHANG Xiaodong,ZHANG Peilin,FU jianping,et al.Applicability analysis of k-εturbulence models on numerical simulation of internal flow field of recoil brake[J].Explosion and Shock Waves,2011,31(5):516-520.
[6]杨玉栋,张培林,郭化平,等.火炮发射冲击载荷对制退机性能的影响研究[J].振动与冲击,2014,33(12):111-116.
YANG Yudong,ZHANG Peilin,GUO Huaping,et al.Effect of gun firing impact load on performance of recoil brake[J].Journal of Vibration and Shock,2014,33(12):111-116.
[7]杨玉栋,张培林,傅建平,等.考虑液体空化的火炮制退机性能分析[J].振动与冲击,2012,31(20):94-98.
YANG Yudong,ZHANG Peilin,FU Jianping,et al.Performance of a gun recoil mechanism considering liquid cavitation[J].Journal of Vibration and Shock,2012,31(20):94-98.
[8]宗士增,钱林方,徐亚栋.火炮反后坐装置动力学耦合分析与优化[J].兵工学报,2007,28(3):272-275.
ZONG Shizeng,QIAN Linfang,XU Yadong.Dynamic coupling analysis and optimization of gun recoil mechanism[J].Acta Armamentarii,2007,28(3):272-275.
[9]杜中华,狄长春.某火炮复杂反后坐装置工作特性仿真分析[J].机械工程师,2011(2):96-99.
DU Zhonghua,DI Changchun.Working characteristic simulation analysis of a gun with complex recoil system[J].Mechanical Engineer,2011(2):96-99.
Mainstream hydraulic resistance coefficient of a cylinder wall groove recoil mechanism
PAN Xiaobin1,SONG Yanming2,TAN Lebin1
(1.School of Mechanical Engineering,Nanjing University of Science and Technology,Nanjing 210094,China;2.Research and Development Center,Inner Mongolia North Heavy Industries Group Co.,Ltd,Baotou 014033,China)
Hydraulic resistance coefficient k1reflecting mainstream channel structure’s characteristic is a key parameter in artillery recoil mechanism design.It can be initialized with tests when channel structures are similar,otherwise it may be different completely.Here,a cylinder wall groove recoil mechanism was studied.For obtaining the reasonable range of k1in theoretic design,the influencing parameters were studied.Based on the mainstream channel structure analysis and reasonable simplification,the piston rod was fixed,the recoil velocity of the recoil rod V was simulated with inlet velocity V′ and the free outlet was set,the equivalent flow field model was built and simulated in Fluent.Under the certain condition of inlet velocity V′ and the channel cross-section area ax,the piston force was calculated.And then,the coefficient k1was deduced with Bernoulli equation.The presented method was validated with a mature recoil mechanism.According to this method,the influences of V and axon k1were studied.It was shown that the coefficient k1increases within a range gradually with decrease in V and axduring recoil; under conditions of the recoil mechanism’s parameters here,and using the comparison between the simulated recoil force and the tested one,the reasonable range of k1is 2.4~2.7.
recoil mechanism; hydraulic resistance coefficient; flow field simulation; recoil force
中国博士后基金(2013M531359)
2015-08-03修改稿收到日期:2016-01-05
潘孝斌 男,博士,讲师,1979年12月生
TJ303.4
A DOI:10.13465/j.cnki.jvs.2016.17.025

