博弈论视角下的物流人才流动问题研究

曹媞

（北京物资学院　劳动科学与法律学院，北京　101149）

博弈论视角下的物流人才流动问题研究

曹媞

（北京物资学院劳动科学与法律学院，北京101149）

指出随着时代的变迁，物流人才成为企业发展最重要的源泉。物流人才的频繁流动给企业的发展带来了很多的问题，如何留住人才是现代人力资源管理的重要问题之一。在对博弈论相关理论进行阐述说明的基础上，构建了物流人才流动博弈模型，分纯策略纳什均衡和混合策略纳什均衡两种情形，探讨物流人才流动中各方的利益诉求和博弈策略，从雇主的挽留成本、雇主的挽留收益、物流人才流动的额外收益、物流人才流动损失和雇主的挽留奖励五个方面探讨了该模型给现实带来的借鉴。

物流人才；人才流动；博弈论；博弈模型

1　引言

随着科学技术的发展，世界的产业结构已经发生了巨大变化。物流业在经济发展中占据着越来越重要的地位。而物流人才是物流企业发展最重要的源泉，这些物流人才也是各物流企业争夺的重心。如何留住物流人才是现代人力资源管理的重要问题之一，因为物流人才的频繁流动给企业的发展带来了很多问题，比如影响企业的生产力、导致企业的技术和商业机密外泄等。因此，对物流企业中人才流动的研究不仅必要，且很重要。

博弈论是研究具有竞争性质现象的数学理论和方法，也是运筹学的一个重要学科，博弈论考虑游戏中个体的预测行为和实际行为，并研究它们的优化策略。在西方社会科学中，博弈论被评为“纪念西方文明发展的十八座里程碑”奖章的第十七位荣膺者，也被认为是20世纪社会科学领域取得的最大成果。利用博弈论工具，探讨物流人才流动中各方的利益诉求和博弈策略，这在现有的文献中较少见，本文将做一个前期探索。

2　人才流失对物流企业的影响

2.1企业中无形资产的流失

科学技术越发达，越显示出人力资本的重要意义。物流人才的流动首先表现为对组织运行的影响。高级物流人才的流失首先会导致企业中专业技术的创新性发生断裂，这可能导致某些技能的断裂，这样就会影响新产品的研发进程或产品的开发。一般来说，企业的技术和技能通常是存在于员工的头脑以及公司的文件和数据库中。“据Delphi集团旗下一家专门从事知识管理和电子学习的新兴技术咨询公司介绍，公司知识的70%存在于员工的头脑中，而只有30%的以外部形式存在。”企业中掌握着核心技术的人才的离开，可能导致企业商业秘密的泄露，对一些物流企业来说影响重大。一般来说，物流人才的流失对企业的影响与其在企业中所处的地位相关，越是核心地位的物流人才，其流动对单位的损失越大。

2.2工作效率下降，企业经营成本增加

通常来说，员工对企业的忠诚度在一定程度上会影响员工的工作效率。当员工决定要离开一家企业时，或者是下岗、任期已到或因为其他原因而不得不离开时，他在心理上就进入了一个对未来新生活的预期阶段。在这个阶段，因为员工把注意力投向了下一份工作或者找工作、退休等状态中，于是就变得没有工作动力，工作效率低下，生产力也便会随之下降，创新能力也相应削弱。

另外，物流人才的流失会使得企业运营成本提高，因为人员的流失，就需要新员工来满足原来岗位的需要，在这个替代过程中，需要经历招聘、培训、新岗位的磨合等，这需要一定的时间。因此，增加了企业的人力资本重置资本。美国的《财富》杂志研究发现：从新员工的招聘到上岗的这个过程，其替换成本达到离职员工年薪的1.5倍。而核心物流人才的离职成本会更高，所以我们认为物流人才的流动会导致企业经营成本增加。

3　博弈论相关理论

3.1博弈论的基本术语和概念

（1）参与人（players）：在一场竞赛或博弈中，每一个有决策权的参与者成为一个参与人。只有两个参与人的博弈现象称为“两人博弈”，而多于两个参与人的博弈称为“多人博弈”。

（2）策略（strategies）：一局博弈中，每个参与人都可以选择实际可行的完整的行动方案，即方案不是某阶段的行动方案，而是指导整个行动的一个方案，一个参与人的一个可行的自始至终全局筹划的行动方案，称为这个参与人的一个策略。如果在一个博弈中参与人都总共有有限个策略，则称为“有限博弈”，否则称为“无限博弈”。

通常用si表示参与人i的一个特定策略，用Si表示参与人i的所有可选择的策略的集合（又称为而i的策略空间）。如果n个参与人没人选择一个策略，那么s=（s1，s2，...，sn）称为一个策略组合。

（3）收益（payoffs）：一局博弈结局时的结果称为收益。每个参与人在一局博弈结束时的得失，不仅与该参与人自身所选择的策略有关，而且与全体参与人所取定的一组策略有关。所以，一局博弈结束时每个参与人的“收益”是全体参与人所取定的一组策略的函数，通常称为收益（payoff）函数。

3.2博弈论的几种均衡

（1）占优策略均衡。由于每个参与人的效用（收益）是博弈中所有参与人的策略的函数，因此每个参与人的最优策略选择依赖于所有其他参与人的策略选择，但在一些特殊的博弈中，一个参与人的最优策略可能并不依赖于其他参与人的策略选择，就是说不论其他参与人选择什么策略，他的最优策略是唯一的，这样的最优策略被称为“占优策略”，也称为“上战均衡”。

（2）重复剔除的占优均衡。在每个参与人都有占优策略的情况下，占优策略均衡是一个非常合理的预测，但在绝大多数博弈中，占优策略均衡是不存在的。由于占优策略均衡在博弈分析中的局限性，需要发展更有效的博弈分析方法。

（3）纳什均衡（纯策略纳什均衡）。现实生活中相当多的博弈，无法使用重复剔除劣策略的办法找出均衡解，那么怎样找出博弈的均衡解呢？需要引入纳什均衡（Nash equilibrium）的概念。纳什均衡是完全信息静态博弈解的一般概念，构成纳什均衡的策略一定是重复剔除严格劣策略过程中不能被剔除的策略。

纳什均衡与占优策略均衡及重复剔除的占优均衡都是博弈分析的方法，它们之间的相互关系如何呢？首先，每—个占优策略均衡、重复剔除的占优均衡一定是纳什均衡，但并非每一个纳什均衡都是占优策略均衡或重复剔除的占优均衡。这是因为一个参与人的占优策略是对于所有其他参与人的任何策略组合的最优选择，它也—定是对于所有其他人的某个特定策略的最优选择，然而，一个策略构成纳什均衡策略的唯一条件是它是参与人对于其他参与人均衡策略的最优选择。在重复剔除过程中，如果最后剩下来的策略组合是唯一的，它—定是—个纳什均衡。其次，纳什均衡一定是在重复剔除严格劣策略的过程中没有被剔除的策略组合，并且是唯一的。

（4）混合策略纳什均衡。如果博弈中不存在纳什均衡或者纳什均衡不唯一，那么纳什均衡分析方法就不能给参与人的选择和博弈结果作明确的预测。这时应用混合策略和混合策略纳什均衡。

在博弈中，一旦每个参与人都竭力猜测其他参与人的策略选择，就不存在纳什均衡，因为这时参与人的最优行为是不确定的，而博弈的结果必然要包含这种不确定性。现在引入混合策略的概念，可以将其解释为一个参与人对其他参与人行为的不确定性。我们将把纳什均衡的定义扩展到包含混合策略，从而可以分析诸如猜硬币、扑克、棒球及战争等博弈出现的不确定性。

相对于这种以一定概率分布在一些策略中随机选择的混合策略，确定性的具体的策略称为“纯策略”，而原来意义上的纳什均衡，即任何参与人都不愿单独改变策略的纯策略组成的策略组合现在可称为“纯策略纳什均衡”。当然，纯策略也可以看作混合策略的特例。纯策略可以看作，选择相应纯策略的概率为1，选择其余纯策略的概率为0的混合策略。混合策略可以看作纯策略的扩展。引进了混合策略的概念以后，可将纳什均衡的概念扩大到包括混合策略的情况。对各参与人的一个策略组合，不管它是纯策略组成的还是混合策略组成的，只要满足各参与人都不会想要单独偏离它，就称之为一个纳什均衡。如果确实是一个严格意义上的混合策略组合构成的纳什均衡，称为“混合策略纳什均衡”。

4　博弈论的基本假设

4.1对参与人的两个基本假设

对参与人的两个基本假设：“理性的”和“智能的”。其中，“理性的”解释如下：如果一个决策者在追逐其目标时能前后一致地做决策，就称他为理性的。广义而言指的是一种行为方式，它同在给定条件或约束下最有效地实现预期目标相关。具体地讲，理性含义如下：（1）存在一组可供选择的备选或替代方案；（2）每一种方案均对应着某种特定的预期净收益或满足程度或目标实现程度；（3）人们总是选择那个能够带来最大预期净收益的方案。“智能的”解释如下：当我们像博弈论专家那样分析一个博弈时，如果参与人知道我们对此博弈所知道的一切，并能做出我们对此博弈所能做出的一切推断，就说此博弈的参与人是智能的。

4.2博弈论的三个基本假设

博弈论的三个基本假设：参与人是理性的；他们有这些理性的共同知识；他们知道博弈规则。

理性的三个基本内涵：理性的参与人具有关于博弈的完全知识；可以确切知道整个状态空间；具有相对无限的逻辑能力。

5　博弈论视角下物流人才流动分析

5.1博弈模型的构建

（1）模型的参数

①参与人。博弈论要求每个参与人必须有可供选择的行动和一个很好定义的偏好函数。那些不作决策的被动主体只当作环境参数来处理。在我国的物流人才流动问题中，物流人才有行为选择的空间，雇主也有行为选择的空间，且他们各自的偏好函数可以定义。

设本文研究的博弈中的参与人为：1和2，参与人1为物流人才，参与人2为雇主。

②策略。参与人1的策略集合S1=｛流动，不流动｝；参与人2的策略集合S2=｛挽留，不挽留｝。其中挽留策略指雇主想办法留住物流人才，可以是正面的办法，如加薪等，也可以是负面的办法，如设置障碍等。

③收益函数。设参与人1的收益函数为u1，参与人2的收益函数为u2。

用G=｛S1，S2；u1，u2｝表述该博弈。

（2）模型的说明。对博弈双方的收益说明如下：

①u1（不流动，不挽留）=X，即正常用工情况下，物流人才的收益为X；u2（不流动，不挽留）=Y，即正常用工情况下，雇主通过雇佣物流人才获得利益Y，也可以说是物流人才为雇主创造的剩余劳动价值Y。

②u1（流动，不挽留）=X+X1，即物流人才选择流动，雇主未挽留，则物流人才得到额外收益X1，最典型的是跳槽行为得到的工资增长和职位升迁；u2（流动，不挽留）=Z，即物流人才流动，雇主未挽留，而招募新人或者用他人替代或者用组织内消化工作的方式，获得收益Z（在招募新人的情况下，应为新人创造的剩余价值与招募成本之差。在他人替代的情形下，应考虑替代人的职位变动前后的价值差。组织内消化工作的方式下，应考虑组织内用工总成本与所消化工作的价值差）。

③u1（流动，挽留）=X+X1-X2，即物流人才流动，被雇主挽留，而物流人才还是选择流动的情形下，将受到损失X2（最典型的是违约金损失）；u2（流动，挽留）=ZC+D，其中C为雇主挽留成本，D为雇主挽留收益（比如违约金收益）。

④u1（不流动，挽留）=X+X3，即物流人才不流动，雇主挽留（主动挽留策略，比如增加福利等），则物流人才获得额外收益为X3；u2（不流动，挽留）=Y-C，即物流人才不流动，雇主挽留，雇主收益为Y-C。

其中的X，X1，X2，X3，Y，Z，C，D均为正数，则得到收益矩阵见表1。

表1　人才流动博弈的收益矩阵

（3）求解模型

①当X1-X2＞X3时，也就是当物流人才流动所获得的收益与因流动遭到的损失之差比雇主为了留住人才而额外提供的利益大时，这时流动是物流人才的优势策略，不论雇主挽不挽留，物流人才都会选择流动。此时存在纯策略纳什均衡，当D＞C时，纯策略纳什均衡为（流动，挽留）；当D＜C时，纯策略纳什均衡为（流动，不挽留）。也就是在这种情形下，物流人才100%的概率会选择流动，而雇主会根据挽留成本和收益来决定是否挽留。

②C＞D时，也就是挽留成本大于收益时，此时，不挽留是雇主的优势策略，不论科技人员是否流动，雇主都选择不挽留；在这种情形下，存在纯策略纳什均衡（流动，不挽留）。也就是雇主留住人才得不偿失，还不如不挽留。

③其他情形存在混合策略纳什均衡，求这个模型的混合策略纳什均衡。求解这个混合策略纳什均衡：

给定q，则1物流人才的收益为：

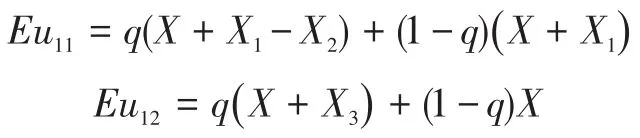
混合策略解的存在要求Eu11=Eu12，得到：

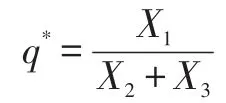
给定p，则2雇主的收益为：

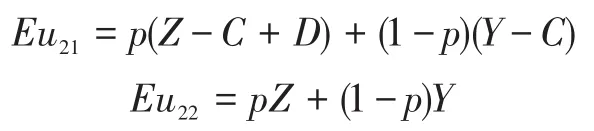
同理可得：

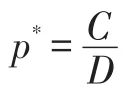
（4）模型分析

①当X1-X2＞X3时，流动是物流人才的优势策略，不论雇主挽留与否，物流人才都会选择流动。此时存在纯策略纳什均衡，当D＞C时，纯策略纳什均衡为（流动，挽留）；当D＜C时，纯策略纳什均衡为（流动，不挽留）。

（2）C＞D时，不挽留是雇主的优势策略，不论物流人才是否流动，雇主都选择不挽留；在这种情形下，存在纯策略纳什均衡（流动，不挽留）。

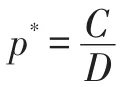
其中C为雇主的挽留成本，D为雇主的挽留收益，X1为物流人才流动的额外收益，X2为物流人才流动损失，X3为雇主挽留奖励。

在这个混合策略纳什均衡中可以看出∶①雇主的挽留成本越高，或者挽留收益越小，物流人才流动的概率就越大；②物流人才流动的额外收益越多，或者流动损失越少，或者雇主挽留的奖励越少，则雇主挽留的概率就越高。

5.2模型的总结

（1）模型中的变量及影响。在这个模型中，我们分情形讨论了纯策略纳什均衡和混合策略纳什均衡：

情形一：纯策略纳什均衡

下面两种情况存在纯策略纳什均衡：①当雇主挽留成本大于收益时，雇主100%选择不挽留；②当X1-X2＞X3时，也就是当物流人才流动所获得的收益与因流动遭到的损失之差比雇主为了留住人才而额外提供的利益大时，流动是物流人才的优势策略，不论雇主挽不挽留，物流人才都会选择流动；

情形二：混合策略纳什均衡

排除纯策略纳什均衡的情形，则存在混合策略纳什均衡：在混合策略纳什均衡中物流人才流动的概率与下面五个因素有关：

①C挽留成本：挽留成本越高，物流人才流动概率越高；

②D挽留收益：雇主挽留收益越高，物流人才流动概率越低；

③X1物流人才流动的额外收益：额外收益越高，则雇主挽留的概率越高；

④X2物流人才流动损失：流动损失越大，则雇主挽留的概率越小；

⑤X3雇主挽留奖励：雇主为了留住人才提供的奖励越多，则挽留的概率越小。

（2）模型对现实的参考意义。结合上面的模型总结，分为以下几个方面探讨其对现实的借鉴：

①雇主的挽留成本。雇主的挽留方式可以分为两种：正面挽留和反面挽留。正面挽留也即通常所为认为的积极挽留，比如提高薪酬待遇和福利待遇等。同时，物流人才相对更看重自己的职业发展以及自己的专业发展，因此，挽留物流人才，还要注重他们专业的发展，为他们提供专业培训，以保证其专业知识能及时更新。个性化的职业生涯规划对物流人才的流动也起到一定的积极挽留作用。反面的挽留，也即通常所认为的消极挽留，比如企业采取档案的控制、合同的到期与否，如果要取得档案的话，必须支付一定的违约金等惩罚性方式。

从以上分析可以看出，无论是正面挽留还是反面挽留，最终雇主都要花费一定的成本。这些成本反应在企业层面上，最终是以经济的形式表达出来。主要表现为：1）雇主用于提高物流人才的薪酬、福利的支出，雇主用于物流人才培训的花费等构成了雇主正面挽留的成本。2）反面挽留的成本主要表现在障碍设置、维护、执行与健全所需要的各种花费。3）由于正面挽留和反面挽留所带来的各种潜在损失。比如，由于组织设置流动的障碍，阻碍了物流人才的流出，但同时也对那些准备流入的人造成一定的障碍。

在现实生活中，我们能看出当雇主留住一个物流人才所需的成本越高时，这个人才的市场价值越高，这可能和市场人才流动机制顺畅程度有关，但是对雇主来说也就越难留住这个物流人才。当雇主挽留成本升高时，物流人才流动的概率越高。

②雇主的挽留收益。挽留收益是在物流人才流动时雇主采取挽留策略所得到的利益。而对当今的科技时代而言，科技知识才是企业真正的创新力和生命力所在。一般来说，雇主决定是否挽留物流人才以及花费多大的人力、物力和财力来挽留，与他们的收益成正比，也称为雇主的挽留收益。一般认为挽留收益包括物流人才能够给雇主带来的收益要大于雇主为了挽留他们而提高薪酬、福利和培训等费用，这样雇主才能获得收益。同时，挽留收益也包括违约金收入、罚金收入等。挽留收益对物流人才的意义在于由于知识存在形式的特殊性，挽留住了物流人才，便就留住了其所拥有的知识。

从以上分析可以看出，当挽留收益越高时，物流人才流动的概率越小。反之，当违约金越高时，员工越不倾向于流动，流动率也越低。

③物流人才流动的额外收益。物流人才流动的额外收益是指物流人才因为选择流动，而获得了工资福利的提高或者职位的升迁。员工的流动往往不是无缘无故的，因为个人在流动时，不仅会产生未来预期的不确定性风险，比如新环境的适应等问题。所以对物流人才来说，只有流动的额外收益越大，他们才越可能选择流动。他们去了工资更高、收入更好的企业，这样也使得他们额外收益得到提高。另外，物流人才本身能够创造的价值越高，则雇主挽留的概率就越大，其流动的额外收益也就越大。

我们可以这样理解这种现象，因为跳槽的工资越高的话，往往代表着物流人才的市场价值越高，所以雇主也越倾向于挽留，那么他们所获的额外收益就越高。

④物流人才流动损失。与物流人才流动的收益对应的是物流人才流动的损失。物流人才流动的损失主要包括薪酬、福利的降低、个人职业前途和地位的降低等。不仅如此，物流人才流动的损失还可能表现为隐形的损失，比如个人的情感因素，一般来说员工在一个单位就职，付出自己的技能、时间和精力的同时，也对企业付出了自己的感情。在原有的单位中会有自己熟悉的人际关系网络，物流人才在流动时离开了熟悉的人际关系网络，需要重新构建自己的社会网络，熟悉新的环境，这些情况对个人心理上所产生的影响是很难用数量来衡量。

物流人才流动损失越大，其市场价值相对也就越低，其跳槽的难度就比较大。物流人才流动损失越大，也说明其能够为雇主带来的价值越小，则雇主挽留的概率越小。那么流动损失越大，则跳槽难度也就相应越大，则雇主越不倾向于挽留。

⑤雇主的挽留奖励。雇主的挽留奖励，包括雇主为了挽留物流人才而提高薪酬及各项福利，也包括为他们提供更好的培训和个人发展空间等收益。一般来说，雇主为了留住物流人才提供的奖励越多，则挽留的概率越小。因为如果雇主已经提供了足够好的挽留奖励仍然留不住该人才的话，他就可能会放弃挽留，或者寻找新的替代者。因为在这种足够优厚的人才政策下，雇主是不愁人才来源的。所以也没有必要坚持留住该人才。从这个角度来说，雇主挽留奖励越多，物流人才越倾向流动，雇主挽留的概率越小。

［1］施锡铨.博弈论［M］.上海∶上海财经大学出版社，2000.

［2］熊勇清，杨羚.员工流动成本构成及度量模型探讨［J］.求索，2005，（6）∶99-101.

［3］汉密尔顿·比兹利，耶利米·博尼奇，大卫·哈顿，著，魏立群，译.持续管理—如何在员工离开时避免知识流失［M］.北京：电子工业出版社，2003.

［4］张维迎.博弈论与信息经济学［M］.上海∶上海人民出版社，2004.

［5］R B Myerson.Nash equilibrium and the history of economic theory［J］.Journal of Economic Literature，1999，37（3）∶1 067-1 082.

［6］W Xin，R Lianwei.Analysis on Public Management and Service Land Valuation Based on Game Theory［A］.In∶setunit. Internet Technology and Ap-plications，2010 International Conference on［C］.2010.

［7］赖茂生，王芳.信息经济学［M］.北京：北京大学出版社，2006.

［8］谢识予.经济博弈论［M］.上海∶复旦大学出版社，2002.

［9］M J Osborne，A Rubinstein.博弈论教程［M］.北京∶中国社会科学出版社，2000.

Study on Flow of Logistics Talents:A Game Theory Perspective

Cao Ti
（School of Labor Science Law， Beijing Wuzi University， Beijing 101149， China）

In this paper， we pointed out that in this era， the logistics talent is one of the most important factors driving the developmentof the enterprises. The frequent displacement of the logistics talents poses a great challenge for the enterprises， thus how to keep these talentsis an important issue in modern human resource management research. On the basis of an illustration of the game theory， we built thelogistics talent flow game model， discussed the claims and game strategies of different parties in the flow of the logistics talents under thepure-strategy Nash equilibrium and the mixed-strategy Nash equilibrium respectively， and then discussed the benefit of the model from theaspects of the persuasion cost and benefit of the employer， the loss and additional benefit from the flow of the logistics talents， and thepersuasion reward of the employer.

logistics talent； talent flow； game theory； game model

F224.32；F259.2

A

1005-152X（2016）03-0073-05

10.3969/j.issn.1005-152X.2016.03.017

2016-02-09

北京物资学院青年课题基金项目“对北京市物流企业员工流动问题研究”（054130340900）

曹媞（1975-），女，安徽颍上人，博士研究生，讲师，研究方向：劳动关系、人才研究等。