九年级数学专题复习中的模型建构探讨
余世豪
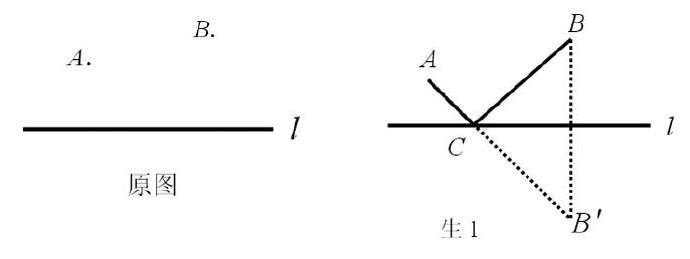
【摘 要】数学模型是数学思维的支撑点,是数学知识的附着点,也是数学应用的突破点;数学模型思想的建立,是学生体会和理解数学与外部世界联系的基本途径。因此,在初中数学教学中,教师应重视模型思想的渗透,让学生经历建立模型,利用模型解题的过程。
【关键词】构建;基本模型;效率
一、教学片段与点评
片段一:构建基本模型,积累经验
出示原题:直线l表示草原上的一条河流,一骑马少年从A地出发让马去河边饮水,然后返回于B地家中,他沿怎样的路线行走,能使路程最短?作出这条最短路线。
生1:只要作点B关于直线l的对称点B,然后连接点B和点A,与直线l的交点为C,连接BC即可。所求的最短路线就是图中的A-C-B。
师:这样作图的依据是什么?
生2:三角形两边之和大于第三边。
生3:应该是“两点之间线段最短”。
师:其实两位同学说的都对。这个问题实际上是利用轴对称变换的思想,把A,B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决。我们可以把这个问题归纳为“马饮水”的数学模型,解决此类问题的方法就是通过作点关于线的对称点,实现化“同”为“异”,化“折”为“直”。
片段二:探究基本模型,深化认识
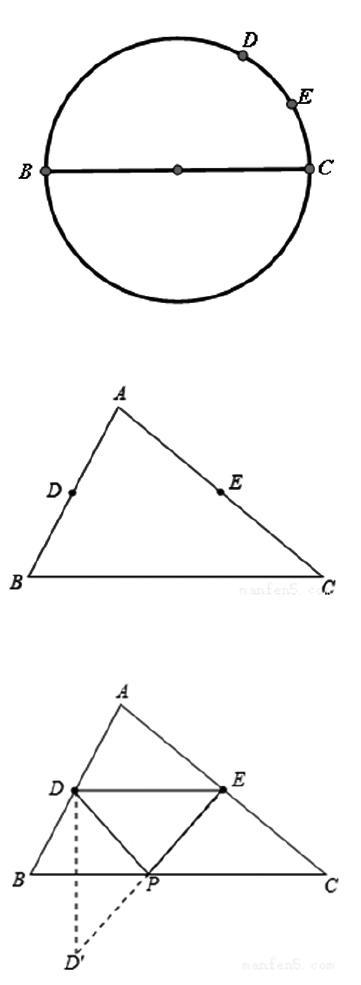
问题1:如图,BC=6cm,以BC为直径作⊙O,D是半圆BC的一个三等分点,E是半圆BC的一个六等分点,P是直径BC上一动点,连接DP、EP,则DP+EP的最小值是 cm。
生4:作点E关于BC的对称点E,连接DE, DE的长度就是所求的最小值……
问题2:如图,BC=6cm,以BC为边作△ABC,点D、E分别是AB、AC边的中点,且BC边上的高为4,BC边上有一动点P,使得△PDE周长最小。
①、请你在BC边上作出点P,保留作图痕迹,不写作法。
②、请直接写出△PDE周长的最小值: 。
生5:作点D关于BC的对称点D,连接ED, 利用勾股定理可求出ED的长度,也就是所求的最小值,所以答案应该是5。
生6:不对。5是PD+PE的最小值,△PDE周长的最小值应该再加上DE的长,正确答案是8……
片段三:拓展基本模型,提升思维
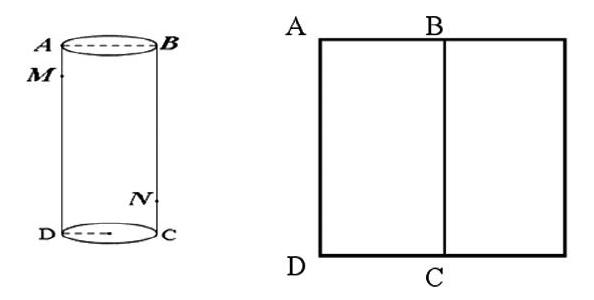
問题3:如图,一个底面半径为1cm,高度为2πcm的无盖圆柱形玻璃容器,A、B两点在容器顶部一条直径的两端,现有一只小甲虫在容器外部A点正下方1cm的M处.
(1)若容器外部B点正下方,距离底部1cm的N处有食物,则这只小甲虫要到N处,最短爬行的距离____cm。
(2)若N点是在容器的内部,则小甲虫最短爬行的距离是____cm。
生7:题(1)只要利用两点之间线段最短,在圆柱的侧面展开图上直接MN就可以了。
生8:题(2)与题(1)相同。
生9:我认为不同,因为食物是在容器的内部,小甲虫在容器外部,所以小甲虫从想点M爬到点N,必须先爬到容器口,所以应该在圆柱的侧面展开图中作点M关于AB的对称点M,连接MN,就可以用勾股定理求出最短路径是cm……
二、教学启示:
(一)数学教学要重视基本模型的构建与挖掘
教师要立足日常课堂教学,有意识地引导学生从中提炼出基本图形,帮助学生归纳和掌握其主要特征和性质,体会蕴涵的数学思想,并运用其解决问题,使学生真正做到解一题,会一类,通一片。这既有利于培养学生“透过现象看本质”的分析问题能力,又可以培养学生的发散性思维,提高解决问题的能力。
(二)数学教学要注重模型思想的渗透
我们在平时的教学中必须重视模型思想的渗透,将数学模型思想寓于具体的概念、法则、实际问题的解决以及一般数学问题的学习和探索中,使学生在对数学规律与方法的探索、归纳和提炼过程中,领会数学模型的涵义,认识数学模型的作用,感受数学模型的思想,体会数学的应用价值,树立数学应用的意识,初步获得发现问题、提出问题、解决简单实际问题的能力。
(三)数学教学要关注学生的最近发展区
作为复习课,教师更应关注学生的最近发展区,让学生主动参与、自主探索,让学生在探索和思考的过程中感悟数学思想,积累数学活动经验。通过教师的引领,让学生在互相交流中互相促进,掌握探究方法;在体验中自主提升,丰富数学思考;在反思中主动生长,构建自己的数学体系;在开放中和谐发展,感受数学之美!

