四色定理的美妙证法

程中战

四色定理命题：

任何一张地图只用四种颜色就能使任意两个相邻的国家着上不同的颜色。

证明：（本文用1 2 3 4代表四种颜色）

公理1：设平面内一个区域（中心区）的周围有n个相邻的区域（邻区），当n为奇数时，所有邻区最多只用三种颜色（n为偶数时只用两种颜色）即可使包括中心区在内的所有两两相邻的区域着上不同的颜色（中心区为第四种颜色）。这种现象称为圆环布局，见图一图二。

在平面内可以任何一个区域为中心区，在它周围没有邻区的线段（或曲线段）上布设若干个邻区，使它们符合新的圆环布局，这条线段（或曲线段）称为空白边，而已經着色的所有区域构成一个不规则（或规则）的版块，这个版块的外边缘是由若干条空白边相连结的不规则环线，称这个环线为空白圈。

公理2：即公理1的推论，任何一条空白边上布设的k个邻区最多只用三种颜色即可填充，就能使其对应的中心区及原有的邻区符合圆环布局。

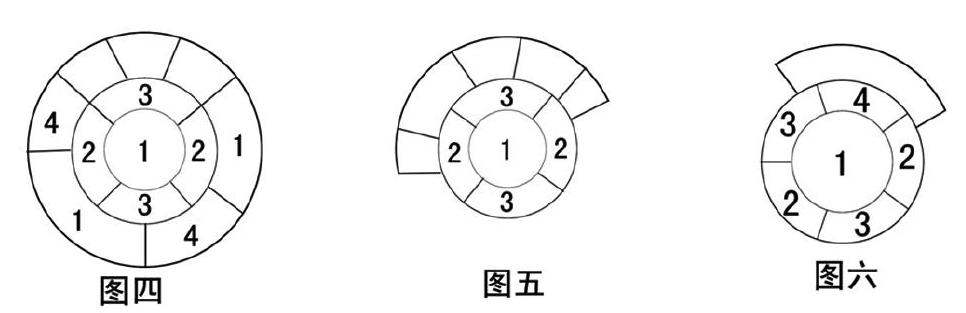
一条空白边的两个端点处有四种情况（如图三图四）：

1.一端有邻区另一端无邻区；2.两端都无邻区；3.两端都有邻区且同色；4.两端都有邻区且异色。据公理1公理2知，以上四种情况，一条空白边上最多只用三种颜色，加上中心区的颜色，共用四种颜色，就能使这个中心区周围的新旧邻区符合圆环布局。同理，无论单条还是多条空白边上布设新的邻区，都符合圆环布局，连续空白边的填充是若干条空白边填充的合成（如图五图六）。这时空白圈向周围扩展，着色版块面积增加，就象涟漪、树木的年轮，又象是中心开花，花瓣层层向周围扩展。

任何一个不规则的空白圈都等价于一个圆，因而，任何一个空白圈内缘的所有区域相连结的图形都等价于一个圆环，故，空白圈内缘上的所有区域最多只用三种颜色即可填充。所以，空白圈外缘上任意弧长的一个邻区（即若干条连续空白边的公共邻区）可用第四种颜色填充（如图六）。

由上可知，四色定理成立。四色定理适合于一个充分大的平面及一个封闭的曲面（如球面）。