基于MCFT方钢管混凝土柱受剪承载力计算模型
王 震,王景全,2†,刘桐旭
(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室,江苏 南京 210096;2.东南大学 国家预应力工程技术研究中心,江苏 南京 210096)
基于MCFT方钢管混凝土柱受剪承载力计算模型
王震1,王景全1,2†,刘桐旭1
(1.东南大学 混凝土及预应力混凝土结构教育部重点实验室,江苏 南京210096;2.东南大学 国家预应力工程技术研究中心,江苏 南京210096)
为准确预测方钢管混凝土柱(square concrete filled steel tube,SCFST)受剪承载力,建立了基于修正压力场理论(modified compression field theory,MCFT)的SCFST受剪承载力计算模型.该模型通过力的平衡和变形协调考虑压弯剪耦合作用,结合对SCFST受剪承载力机制的分析,推导出了计算SCFST受剪承载力的一般公式.注意到SCFST在试验中出现了两种不同的剪切破坏模式,模型分别给出了相应的破坏判别条件.利用SCFST受剪承载力计算模型对收集到的17根试件进行计算,所得结果与试验值吻合较好.研究发现,SCFST受剪承载力计算模型不仅可以计算SCFST在压弯剪共同作用下的受剪承载力,而且可以对SCFST的破坏模式进行判断,结果可信,可用于SCFST受剪承载力计算.
钢管混凝土;受剪承载力;理论模型;修正压力场理论;破坏模式
方钢管混凝土(square concrete filled steel tube,SCFST)柱因具有对建筑布局影响小等优点,在高层建筑和空间结构中得到了广泛应用[1-2].通常认为,SCFST柱在进行压弯作用设计时,其受剪承载力能够满足设计要求而无需进行验算[3].但随着工程实践的发展,在一些情况下,如SCFST结构用作支撑空间网壳的短柱时[4],构件会承受很大的剪力,为保证结构安全,需要对SCFST柱的受剪承载力做出合理准确的估计.故有必要针对SCFST柱的受剪承载力进行专门研究.
目前,针对SCFST柱受剪承载力开展的研究还很少.Tomii和Sakino[5]进行了40根恒定轴压下SCFST柱受剪承载力的试验研究,主要考察了轴压比、剪跨比和截面宽厚比等参数的影响;尧国皇[6]利用Abaqus有限元模型分析了SCFST柱在压、弯、扭、剪及其复合受力状态下力学性能,并在参数分析的基础上给出了承载力的实用计算方法;陈宇超[7]借助Abaqus有限元模型讨论了不同受力状态下矩形钢管混凝土承载力随主要参数的变化规律;黄勇等[4]进行了6根SCFST短柱的无轴力受剪承载力试验,对试件分别施加水平单调荷载和往复荷载,并对试验结果进行了有限元模拟;蔡健等[8]进行了6个足尺SCFST柱的受剪承载力试验,分析剪跨比和轴压比等因素对试件受剪承载力的影响,并对试件的受剪性能进行了有限元分析;郭淑丽和陶忠[9]进行了10根SCFST短柱的受剪承载力试验,重点考察了剪跨比、轴压比、混凝土强度和钢管强度等参数对SCFST短柱受剪承载力的影响.然而,对SCFST柱受剪承载力的研究目前仍停留在试验研究和有限元模拟阶段,缺乏相应的理论计算模型.本文基于修正压力场理论(modified compression field theory,MCFT)[10],建立了可用于计算压弯剪作用下SCFST柱受剪承载力的理论模型,并通过与已有试验资料比较,证明了理论模型的正确性.
1 方钢管混凝土柱受剪承载力计算理论模型
1.1理论模型的基本思路
SCFST柱底截面承受的轴力、剪力和弯矩最大,是构件上最容易发生破坏的部位.因此,选择柱底部分作为研究对象,通过对正截面分析确定压弯作用下方钢管混凝土柱底部截面的应变分布,并选择截面中心处正应变εo作为MCFT中的平均纵向应变εx[11-12],用于考虑压弯作用对受剪承载力的影响(见图1).

图1 方钢管混凝土柱受剪承载力计算理论模型
1.2MCFT
1.2.1变形协调条件
假定钢管与混凝土之间变形完全协调,即
εx=εcx=εsx.
(1)
εz=εcz=εsz.
(2)
γ=γc=γs.
(3)
式中:εx,εz和γ分别为单元平均纵向应变、平均横向应变和平均剪应变;εcx,εcz和γc分别为混凝土平均纵向应变、平均横向应变和平均剪应变;εsx,εsz和γs分别为钢管腹板平均纵向应变、平均横向应变和平均剪应变.
根据混凝土摩尔平均应变圆有:

(4)
εc1=εcx+εcz-εc2.
(5)

(6)
式中:εc1和εc2分别为混凝土主拉应变和主压应变;θ为混凝土主压应变角.
1.2.2平衡条件
方钢管混凝土柱中钢管翼缘以承担纵向应力为主,因此,假定钢管翼缘部分剪应力为零[13],则有:
σx=σcx+ρstσstx+ρswσswx.
(7)
σz=σcz+ρswσswz.
(8)
τ=τc+ρswτsw.
(9)
式中:σx,σz,τ分别为单元平均纵向应力、平均横向应力和平均剪应力;σcx,σcz,τc分别为混凝土平均纵向应力、平均横向应力和平均剪应力;σstx为钢管翼缘平均纵向应力;σswx,σswz,τsw分别为钢管腹板平均纵向应力、平均横向应力和平均剪应力;ρst=2t/h和ρsw=2t/b分别为钢管翼缘含钢率和钢管腹板含钢率.由于水平荷载仅作用在柱顶,柱身不受水平均布荷载作用,故σz=0[14];由于忽略钢管翼缘的剪应力,故单元平均剪应力仅由混凝土平均剪应力τc和钢管腹板平均剪应力τsw两部分组成.
根据混凝土摩尔平均应力圆,并假定混凝土主压应力角和主压应变角一致[10]:
σcx=σc1-τccot θ.
(10)
σcz=σc1-τctan θ.
(11)

(12)
式中:θ为混凝土主压应力角;σc1和σc2分别为混凝土主拉应力和主压应力.
钢筋混凝土柱在柱顶水平荷载和轴力共同作用下发生剪切破坏时的危险部位是斜裂缝处,因此有必要对裂缝处的局部受力条件进行专门研究.而从收集到的方钢管混凝土柱受剪承载力试验[9](如图2)可以看出,因钢管作为整体对核心混凝土具有较强的约束作用,方钢管混凝土柱发生剪切破坏时并非沿斜裂缝进行,故本文对方钢管混凝土柱裂缝处的局部应力不再进行专门研究,虽然混凝土裂缝处钢管腹板应力比平均应力略高,但仍假设两者一致.

图2 发生不同剪切破坏模式的试件
1.3正截面分析
εx对混凝土主压应力角θ影响显著,因而其对柱底受剪影响很大.柱承受轴力、弯矩和剪力的共同作用,轴力和弯矩在柱底截面上产生正应变.选取柱底截面中心处正应变εo作为εx(如图3),则在进行受剪承载力计算时,需要首先计算柱底截面在轴力和弯矩作用下产生的正应变εo.
εo可采用截面纤维模型进行柱底截面分析得到,如图3所示,截面分为钢管和钢管约束混凝土两种纤维,每一个纤维用各自中心处的应变作为平均应变.在截面形心处作用一个不变的轴压力P,对一个给定截面曲率φi,采用一种区间搜索法[15]确定其相应的中性轴深度xn,考虑平截面假定及材料本构关系,可以确定出截面应变、应力分布,对全截面进行积分即可获得相应的截面抵抗弯矩M.

图3 方钢管混凝土柱截面纤维模型
由平截面假定可知,修正压力场模型中的平均纵向应变

(13)
钢管约束混凝土采用韩林海模型[16],见图4(a),图中σo和εo分别为钢管约束混凝土峰值压应力及其对应压应变,具体表达式如下:
(14)
式中参数计算如下:
σo=

A=2.0-K;B=1.0-K;K=0.1ξ0.745;


εcc=1300+14.93fck;λ=1.60+1.5(εo/εc);
β=
式中:Aa为钢管面积;fy为钢管屈服强度;Ac为管内混凝土面积;fck为无约束混凝土抗压强度标准值.
钢材本构关系分为弹性阶段、塑性阶段、强化阶段和下降阶段[17],见图4(b),具体表达式如下:
fs=
(15)
式中:εy为钢材的屈服应力和屈服应变;Es为钢材弹性模量;εsh为强化应变;fsu和εsu分别为钢材的最大应力和相应的应变;fsb和εsb分别为钢材的断裂应力和相应的应变.

(a)钢管约束混凝土应力应变关系 (b)钢材应力应变关系
1.4受剪承载力的一般计算式
将式(11)代入式(8),得到
σz=σc1-τctan θ+ρswσswz.
(16)
由于σz=0[13],得到
τc=σc1cot θ+ρswσswzcot θ.
(17)
将式(17)代入式(9),得到
τ=σc1cot θ+ρswσswzcot θ+ρswτsw.
(18)
方钢管混凝土柱受剪承载力
V=τbhv.
(19)
式中:b为截面宽度,hv为有效受剪高度,一般取hv=0.9h,h为截面高度,则
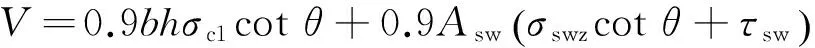
(20)
式(20)即方钢管混凝土柱受剪承载力的一般计算式,可以看出方钢管混凝土柱受剪承载力由管内混凝土和钢管腹板两部分提供,其中钢管腹板通过横向正应力和剪应力两种途径提供了受剪承载力.
1.5剪切破坏的两种模式
在收集到的方钢管混凝土柱受剪承载力试验中[4,8-9],按照试验现象可以将剪切破坏分为两种模式:一种模式是钢管腹板出现具有一定方向性的裂纹线,柱底部分钢管有明显外鼓现象,但核心混凝土仍旧保持完整;另一种模式是试件受压侧钢管被剪断,断面处的骨料被剪断,混凝土被压碎呈粉末状流出.第一种模式是以钢管腹板单元在平面应力作用下到达强度极限为标志,第二种模式是以混凝土单元在平面应力作用下主压应力达到强度极限为标志.显然,第一种破坏模式的延性较好.
1.6两种剪切破坏模式的承载力计算
基于MCFT计算受剪承载力,因为参数太多,需要迭代计算,比较繁琐.本文采用图解法求解方钢管混凝土柱的受剪承载力,避免了迭代计算,具体计算步骤如下:
将式(9)代入式(19),可得

(21)
对于柱底截面给定一个曲率φi,可以求得截面弯矩M和修正压力场模型中的平均纵向应变εx=εo,由式(1)知εcx=εsx=εx,假定σcx和εcx满足方钢管约束混凝土应力应变关系,当σcx和εcx为负即为压应力和压应变,遵守式(14);当σcx和εcx为正即为拉应力和拉应变,遵守下式
(22)
式中:εcr为混凝土开裂应变.
假定σswx和εsx满足理想弹塑性模型,拉压等强,由广义胡克定律知

(23)

(24)
将上两式代入式(2)和式(8)中,又知σz=0,可以得到
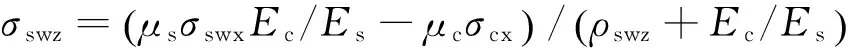
(25)
又由广义胡克定律知

(26)

(27)
由式(3)知γc=γs,将式(23)和式(24)代入式(3),得到

(28)
已知方钢管混凝土柱剪切破坏模式1的破坏条件是以钢管腹板单元在平面应力作用下到达强度极限为标志,由第三强度理论知,当钢管腹板达到强度极限时,满足

(29)
由上式整理得

(30)
将式(30)代入式(28)中,可以得到钢管腹板达到强度极限时对应的混凝土剪应力

(31)
将式(30)和式(31)代入式(21),得到钢管腹板达到强度极限时对应的受剪承载力Va.曲率φ变化时Va随着变化,实际得到的是Va-φ曲线.
剪切破坏模式2是以混凝土单元在平面应力作用下主压应力达到强度极限为标志,可保守地认为发生剪切破坏模式2时混凝土主压应变εc2=εo[13],此时的混凝土主压应力σc2=βσo,β为考虑主拉应变影响的折减系数,其表达式如下
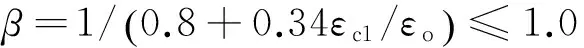
(32)
将式(10)代入式(12),整理得

(33)
其中,将式(25)代入式(24),可以求得εsz,由式(2)知εcz=εsz,又知εcx=εx和εc2,由式(6)可以得到

(34)
将式(33)代入式(28)中,得到混凝土主压应力达到强度极限时对应的钢管腹板剪应力
τsw=

(35)
将式(33)和式(35)代入式(21),可以得到混凝土主压应力达到强度极限时对应的受剪承载力Vc.同理,因曲率φ可以改变,实际得到的是Vc-φ曲线.
因SCFST发生剪切破坏时剪跨比都很小,可不计P-δ效应,由截面弯矩确定的柱顶水平荷载
Vf=M/L.
(36)
文献[18]通过试验研究发现对于偏心受压钢管混凝土构件,钢管最大压应变达0.01时所对应的荷载值与同试验中的最大荷载值相比相差不大,可以近似地以该值作为极限荷载值.因此,本文选取钢管受压应变达到0.01作为方钢管混凝土柱弯曲破坏的判断依据.
将Vf-φ,Va-φ和Vc-φ绘制在同一坐标系下,如果SCFST达到弯曲破坏前,Vf始终小于Va和Vc,则可以认为SCFST没有发生剪切破坏,以弯曲破坏时对应的水平荷载值作为受剪承载力.如果SCSFT达到弯曲破坏前,出现Vf小于Va和Vc的情况,即Vf-φ曲线与Va-φ曲线或Vc-φ曲线相交,则认为SCFST发生剪切破坏.当Vf-φ曲线与Va-φ曲线首先相交时,则认为方钢管混凝土柱发生模式1的剪切破坏,两条曲线的交点对应的水平荷载值作为受剪承载力;否则认为SCFST发生模式2的剪切破坏,具体计算流程见图5.

图5 建议模型计算流程图
2 试验验证
利用本文推导的受剪承载力计算模型对收集到的17根试件进行计算,得到的计算结果及试件的设计细节详见表1.图6则给出了不同破坏模式下SCFST受剪承载力的图解示意图.由表1可以看出,利用本文受剪承载力计算模型得到的受剪承载力与试验值吻合较好,变异系数仅为6.41%,满足工程精度要求.对于满足规范关于壁厚要求的方钢管混凝土柱,在压剪弯共同作用下,方钢管能够对核心混凝土形成有效约束并且不易发生屈曲.对此类构件进行受剪承载力计算,建议模型都是适用的.

曲率φ/m-1 曲率φ/m-1
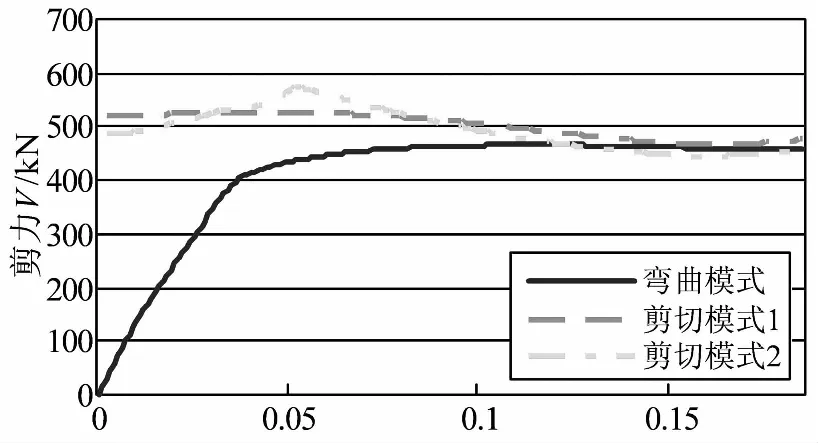
曲率φ/m-1

编号B/mmt/mmLin/mmfy/MPafc/MPaP/kNVex/kNV/kNV/Vex破坏模式C1[3]6002054046056.20905798521.088弯曲C26002054046056.2443310154106641.050弯曲C36002039046056.2011192118701.061剪切(模式1)C46002039046056.2443311968126001.053剪切(模式1)A1[7]150430030634.20187.5198.61.059弯曲 A2150430030634.20215.7198.60.921弯曲A3150430030634.20198.2198.61.002弯曲S12-C1-1[8]12025133831.902642901.098剪切(模式1) S12-C1-212025133831.976.73233421.059剪切(模式1)S12-C1-312025133831.9153.43843871.008剪切(模式1)S12-C1-412025133831.9184.0391.53951.009剪切(模式1)S12-C1-512025133831.9230.0429.54000.931剪切(模式1)S11-C1-312023333831.9153.4400.54031.006剪切(模式1)S13-C1-3120213533831.9153.4150.51460.970弯曲S14-C1-3120219533831.9153.41341150.858弯曲S12-C2-312025133857.4277.2445.54691.030剪切(模式1)S22-C1-312035141531.9153.44354681.076剪切(模式2)
注:V/Vex平均值为1.016,变异系数为6.41%.
3 结 论
本文基于MCFT建立了关于SCFST的受剪承载力计算模型.该模型可以考虑压弯剪耦合作用,不仅给出了SCFST受剪承载力计算的一般公式,而且对SCFST两种不同的剪切破坏模式进行了区分,分别给出了相应的破坏判别条件.通过与收集到的17根试件的试验值进行对比,发现模型计算结果与试验值吻合较好,该模型可以用于SCFT在压弯剪共同作用下受剪承载力的预测与破坏模式的识别.
[1]聂建国,秦凯.方钢管混凝土柱节点受剪承载力受力性能的研究[J].建筑结构学报,2007,28(4): 8-17.
NIE Jian-guo,QIN Kai.Research on shear performance of concrete-filled square steel tubular column connections[J].Journal of Building Structures,2007,28(4): 8-17.(In Chinese)
[2]黄远,朱正庚,杨扬,等.端部设肋方钢管混凝土框架柱抗震性能分析[J].湖南大学学报: 自然科学版,2016,43(1): 89-96.
HUANG Yuan,ZHU Zheng-geng,YANG Yang,et al.Seismic analysis of the square concrete-filled steel tube frame column with end ribs[J].Journal of Hunan University: Natural Sciences,2016,43(1): 89-96.(In Chinese)
[3]CECS 159: 2004矩形钢管混凝土结构技术规程[S].北京: 中国计划出版社,2004: 21-24.
CECS 159: 2004Technical specification for structures with concrete-filled rectangular steel tubular members[S].Beijing: China Planning Press,2004: 21-24.(In Chinese)
[4]黄勇,陈伟刚,段莉.钢管混凝土短柱 (剪力键) 受剪性能试验研究[J].建筑结构学报,2011,32(12): 178-185.
HUANG Yong,CHEN Wei-gang,DUAN Li.Experimental study on shear resistance performance of concrete filled steel tube shear block stub columns[J].Journal of Building Structures,2011,32(12): 178-185.(In Chinese)
[5]TOMII M,SAKINO K.Experimental studies on concrete filled square steel tubular beam-columns subjected to monotonic shearing force and constant axial force[J].Journal of Architecture and Planning,1979,281: 81-90.
[6]尧国皇.钢管混凝土构件在复杂受力状态下的工作机理研究[D].福州: 福州大学土木工程学院,2006: 262-280.
YAO Guo-huang.Research on behavior of concrete-filled steel tubes subjected to complicated loading states[D].Fuzhou: College of Civil Engineering,Fuzhou University,2006: 262-280.(In Chinese)
[7]陈宇超.矩形钢管混凝土构件复合受力时力学性能与设计方法研究[D].兰州: 兰州理工大学土木工程学院,2009: 60-67.
CHEN Yu-chao.Research on mechanical performance and design method of concrete-filled rectangular steel tube subjected to complex force[D].Lanzhou: College of Civil Engineering,Lanzhou University of Technology,2009: 60-67.(In Chinese)
[8]蔡健,梁伟盛,林辉.方钢管混凝土柱受剪承载力性能试验研究[J].深圳大学学报: 理工版,2012,29(3): 189-194.
CAI Jian,LIANG Wei-sheng,LIN Hui.Experimental study on shear resistance performance of concrete filled square steel tubular columns[J].Journal of Shenzhen University Science and Engineering,2012,29(3): 189-194.(In Chinese)
[9]郭淑丽,陶忠.方钢管混凝土柱抗剪试验研究[J].福建工程学院学报,2012,9(6): 550-554.
GUO Shu-li,TAO Zhong.Experimental study of square concrete-filled steel tube columns subjected to shearing[J].Journal of Fujian University of Technology,2012,9(6): 550-554.(In Chinese)
[10]VECCHIO F J,COLLINS M P.The modified compression-field theory for reinforced concrete elements subjected to shear[J].ACI Structural Journal,1986,83(2): 219-231.
[11]MOSTAFAEI H,VECCHIO F J,KABEYASAWA T.Deformation capacity of reinforced concrete columns[J].ACI Structural Journal,2009,106(2): 187-195.
[12]MOSTAFAEI H,KABEYASAWA T.Axial-shear-flexure interaction approach for reinforced concrete columns[J].ACI Structural Journal,2007,104(2): 218-226.
[13]朱伟庆,贾金青,孟刚.基于修正压力场理论的型钢超高强混凝土柱受剪承载力研究[J].建筑结构学报,2013,34(10): 101-107.
ZHU Wei-qing,JIA Jin-qing,MENG Gang.Shear strength of steel reinforced high strength concrete columns based on modified compression field theory[J].Journal of Building Structures,2013,34(10): 101-107.(In Chinese)
[14]BENTZ E C,VECCHIO F J,COLLINS M P.Simplified modified compression field theory for calculating shear strength of reinforced concrete elements[J].ACI Structural Journal,2006,103(4): 614-624.
[15]BAI Z Z,AU F T K.Ductility of symmetrically reinforced concrete columns[J].Magazine of Concrete Research,2009,61(5): 345-357.
[16]廖飞宇,韩林海.方形钢管混凝土叠合柱的力学性能研究[J].工程力学,2010,27(4): 153-162.
LIAO Fei-yu,HAN Lin-hai.Performance of concrete-filled steel tube reinforced concrete columns with square sections[J].Engineering Mechanics,2010,27(4): 153-162.(In Chinese)
[17]范立础,卓卫东.桥梁延性抗震设计[M].北京: 人民交通出版社,2001: 152-153.
FAN Li-chu,ZHUO Wei-dong.Bridge seismic ductility design[M].Beijing: China Communications Press,2001: 152-153.(In Chinese)
[18]陈宝春,王来永,欧智菁,等.钢管混凝土偏心受压应力-应变试验研究[J].工程力学,2003,20(6): 154-159.
CHEN Bao-chun,WANG Lai-yong,OU Zhi-qing,et al.Experimental study of stress-strain relation of eccentrically-loaded concrete-filled steel tubular columns[J].Engineering Mechanics,2003,20(6): 154-159.(In Chinese)
Shear Capacity of Square Concrete Filled Steel Tube Columns Based on Modified Compression Field Theory
WANG Zhen1,WANG Jing-quan1,2†,LIU Tong-xu1
(1.Key Lab of Concrete and Prestressed Concrete Structure of Ministry of Education,Southeast Univ,Nanjing,Jiangsu210096,China;2.National Prestress Engineering Research Center,Southeast Univ,Nanjing,Jiangsu210096,China)
To accurately predict the shear capacity of square concrete filled steel tube (SCFST) columns,a theoretic model was established based on modified compression field theory.In this model,compatibility and equilibrium relationships were taken to consider the axial-flexure-shear interaction,and a general formula of shear capacity of SCFST was deduced by dissecting shear mechanism.Due to two different failure modes observed in previous tests,two different failure criterions were given respectively.The proposed model was applied to the 17 existing column specimens,which predicted well the shear capacities of the test specimens.The results show that the proposed model not only can be utilized to evaluate shear capacity of SCFST subjected to axial force,flexural moment,and shear force,but also can be employed to verdict different failure modes.The calculation results of the proposed model are credible,and the model is effective.
concrete filled steel tube; shear capacity; theoretic model; modified compression field theory; failure mode
1674-2974(2016)09-0051-08
2015-10-10
国家科技支撑计划项目(2011BAJ09B02);江苏省“六大人才高峰”第十一批资助项目(JZ-007);江苏高校优势学科建设工程资助项目(CE02-1-4)
王震(1990-),男,山东菏泽人,东南大学博士研究生
†通讯联系人,E-mail: wangjingquan@seu.edu.cn
TU392.3
A

