基于断裂力学的锚拉板疲劳寿命评估

李立峰，唐　武，唐金良

(湖南大学 土木工程学院，湖南 长沙　410082)



基于断裂力学的锚拉板疲劳寿命评估

李立峰†，唐武，唐金良

(湖南大学 土木工程学院，湖南 长沙410082)

为研究斜拉桥锚拉板结构的疲劳性能，以一座叠合梁斜拉桥为例，采用最新钢桥规范的疲劳荷载模型加载并按雨流法处理计算了疲劳荷载谱，结合空间实体有限元模型，识别了锚拉板的典型构造细节并获得疲劳应力谱；在典型构造细节处引入初始表面裂纹，计算了裂纹尖端的应力强度因子，回归分析得到应力强度因子与裂纹尺寸的关系式，代入Paris公式积分得到了各典型构造细节的疲劳寿命，从而建立了基于断裂力学的锚拉板疲劳寿命分析方法.研究结果表明：基于断裂力学方法得到的锚拉板疲劳寿命超过了100年，满足设计及使用要求；裂纹初期扩展很慢，当尺寸达到10 mm时，已消耗了60%～80%的疲劳寿命，应及时加以补强.

断裂力学；锚拉板；疲劳寿命；应力强度因子；Paris公式

钢斜拉桥结构中，索梁锚固构造是关键受力部位，其种类很多，而锚拉板[1]具有构造简单、安装方便、传力明确等突出优点，近年来得到广泛应用.但由于焊缝多、应力集中，疲劳问题突出，因此合理评估其疲劳寿命具有重要意义[2].

目前，钢结构的疲劳寿命评估主要是基于S-N曲线和Miner线性累积损伤理论[3]，即对特定的构造细节选取相应类别的S-N曲线进行分析.该方法应用广泛，但也存在不足：复杂构造细节无合适的S-N曲线对应；实际工程中大部分构件处于带裂纹工作状态，无法采用S-N曲线进行分析.对于裂纹如何扩展、结构剩余寿命多少，需要借助断裂力学进行分析[4].

目前不少学者正致力于研究断裂力学理论在钢桥疲劳寿命分析中的应用.王元清等[5-6]完成了多个不同试件的紧凑拉伸试验，得到了基于Paris公式的疲劳裂纹扩展性能参数，通过对比有限元结果与试验结果，验证了数值方法分析复合型疲劳裂纹扩展的可靠性.彭鲲等[7]用断裂力学方法研究波形钢腹板组合箱梁的疲劳寿命计算模式，推导了结构的S-N曲线.王春生等[8]用断裂力学方法对老龄铆接钢桥剩余寿命和使用安全进行了评估.童乐为等[9]利用断裂力学方法预测了圆钢管混凝土T型焊接节点的疲劳寿命，研究表明断裂力学可较好地预测该结构的疲劳寿命.上述研究推动了断裂力学理论在实际工程中的应用，但是在锚拉板疲劳寿命分析方面的研究还比较少，如何用断裂力学理论对锚拉板疲劳寿命进行合理评估还需要深入研究.本文结合一座叠合梁斜拉桥，建立了全桥三维有限元模型，选用最新钢桥规范中疲劳荷载模型并用雨流计数法处理得到了索力荷载谱；结合锚拉板结构的三维实体有限元分析模型，得到典型构造细节的疲劳应力谱；引入半椭圆形初始表面裂纹，按经典公式得到裂纹尖端的应力强度因子，回归分析得到应力强度因子与裂纹尺寸之间的关系式，再对Paris公式积分，从而获得锚拉板结构的疲劳寿命.

1　工程概况

乌江特大桥是贵州省内的大跨混合体系叠合梁斜拉桥，双塔双索面、半漂浮体系，跨径布置为54 m+71 m+360 m+71 m+54 m，全长610 m.设计行车速度80 km/h，双向六车道，设计荷载为公路I级.索梁锚固结构为锚拉板式，如图1所示.桥宽28 m，边跨为混凝土 “π”形主梁，中跨为“上”字形钢主梁结合桥面板的整体断面(图2)；单个主塔布置28对斜拉索，设计索力由2 333.4 kN变化到5 184.5 kN.

图1　中跨尾索处锚拉板构造图(mm)

图2　1/2中跨主梁断面图(mm)

锚拉板式索梁锚固结构由锚拉板、加劲板、锚筒、锚垫板和装饰圆板等构成.在锚拉板中部开槽，锚筒通过双面单V形焊缝(焊缝1)与两侧槽口相连；斜拉索穿过锚筒锚固在锚垫板上；在两侧焊接加劲板以补偿开槽对锚拉板的削弱，并增强横向刚度和整体性；锚拉板通过双面V形焊缝(焊缝2)与主梁腹板连接.索力通过焊缝1以剪力形式传递至锚拉板，再由焊缝2传递至钢主梁.焊缝2承受竖向、纵向拉应力和剪应力的共同作用，应力状态复杂.锚拉板由工厂整体加工，在施工现场通过焊缝2与钢主梁相连.

锚拉板受力复杂，在移动荷载作用下疲劳问题尤为突出，而且对其中部分构造细节的疲劳性能缺乏深入研究.因此本文拟利用断裂力学理论对其疲劳性能进行合理评估，具体的分析步骤如图3所示.

2　疲劳荷载计算

采用桥梁软件Midas建立全桥三维杆系有限元分析模型，斜拉索用空间桁架单元模拟，塔和钢主梁用空间梁单元模拟，塔、墩底约束采用一般支撑约束模拟.全桥共有节点689个；单元570个，其中桁架单元112个，梁单元458个，如图4所示.全桥计算结果表明：活载作用下中跨尾索的索力幅最大，其对应锚拉板的受力最具有代表性.求得中跨尾索各个车道的索力影响线，图5为近侧慢车道(车道1)索力影响线.

图3　分析流程图

图4　全桥有限元模型

距离/m

锚拉板的疲劳荷载即为活载引起的斜拉索索力幅.根据文献[10]，偏安全地选取疲劳荷载模型I进行索力幅的计算.

疲劳荷载模型I是将文献[10]中的公路I级的车道荷载进行折减，即集中力为P=0.7×360=252 kN，均布荷载为q=0.3×10.5=3.15 kN/m.将折减后的车道荷载按索力影响线加载，采用雨流计数法处理，获得各个车道产生的索力幅如表1所示.

表1　各个车道的索力幅

考虑6车道横向折减系数0.55，索力幅δF为：

δF=0.55×385.88=212.2kN.

(1)

荷载循环次数可偏安全地考虑为：疲劳车队以设计车速80 km/h通过桥梁，则每年荷载循环次数为：

(2)

3　典型细节应力脉分析

锚拉板焊缝较多，若对每处构造细节进行疲劳寿命分析，工作量巨大也不经济.研究表明，疲劳破坏起源于高应力或高应变的局部[11].因此，首先要识别最可能出现疲劳破坏、且一旦出现破坏将直接导致锚拉板无法继续承载的典型构造细节.

参照桥梁实际情况，利用有限元软件ANSYS建立锚拉板结构精细空间有限元模型：以拉索锚固点为中心，往两侧各取6 m，横向选取半桥宽；锚拉板及主梁用四节点三维空间板壳单元Shell181，桥面板采用Solid45实体单元建立，主梁纵向两端约束全部位移，横向施加对称约束；索力以面荷载形式施加在锚垫板，如图6所示.结合锚拉板空间应力分析结果(图7)，选取典型构造细节如下：

a)锚拉板与锚筒间的双面单V形焊缝下端，由于几何形状的突变而导致明显的应力集中.此外，由于该处空间较小，在斜拉索安装等过程容易产生各种初始缺陷，成为“裂纹源”.因此取A，B点为本文分析的典型构造细节之一.

b)锚拉板与腹板间的双面V形焊缝两端的C，D点由于截面形状的突变，也存在一定程度的应力集中现象，而且焊缝两端板厚相差较大(锚拉板50 mm，腹板30 mm)，导致力线分布不均匀，当存在焊接初始缺陷时，很容易出现疲劳破坏，因此选取C，D点作为典型构造细节进行分析.

在前文求得的疲劳荷载和最不利索力作用下，各典型构造细节的应力如表2所示.

图6　锚拉板有限元模型

图7　锚拉板应力分布及典型构造细节(MPa)

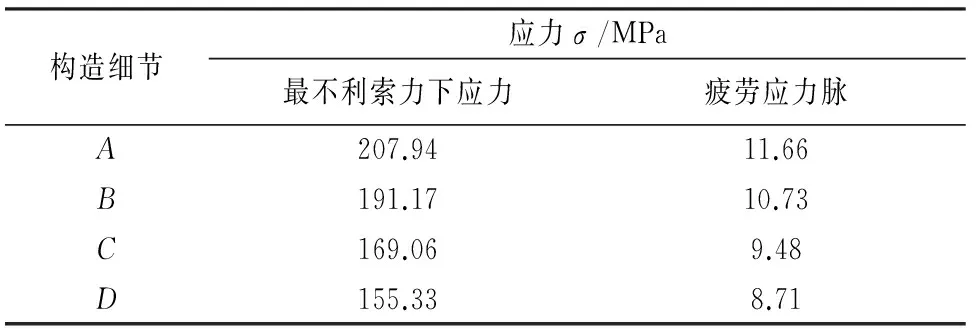
构造细节应力σ/MPa最不利索力下应力疲劳应力脉A207.9411.66B191.1710.73C169.069.48D155.338.71

4　初始裂纹尺寸

对于典型焊接细节，最常见的初始裂纹是半椭圆形的表面裂纹，一般出现在焊趾处.初始裂纹尺寸可通过超声波探测、磁粉探测、X光探测等无损检测方法获得.每种方法均有各自的检测界限，通常不会小于1 mm.但对于新建桥梁初始裂纹往往很小，无法通过上述方法获得.根据文献[7]，钢桥的焊接构造细节处会存在0.02～0.2 mm大小的初始缺陷，因此偏安全地取初始裂纹深度a0=0.2 mm.

5　临界裂纹尺寸

临界裂纹是指构件发生破坏或不能继续承载时的裂纹尺寸.工程上临界裂纹的确定方法通常有K准则和适合承载准则.

使用K准则时，临界裂纹尺寸与材料的断裂韧性相关，根据文献[11]，其表达式为：

(3)

式中：KIC是材料断裂韧性，通过试验获得；f是与构件几何和裂纹形状相关的修正系数，可由《应力强度因子手册》[12]查得；σ为循环应力，见表2.

适合承载准则是指在满足正常使用要求下，根据构件的实际形状选择一个确定尺寸作为临界裂纹尺寸.对于上述焊接细节，当裂纹深度达到板厚时，即可认为构件已发生破坏，因此取为板件厚度ac2.

最终确定的临界裂纹尺寸为：

ac=min (ac1,ac2).

(4)

6　疲劳寿命预估

6.1疲劳寿命

裂纹的扩展速率可用da/dN-δK曲线来描述，如图8所示.图中δKth为门槛应力强度因子幅值，是裂纹是否扩展的控制参数.对于焊接细节，由于焊接残余拉应力很高，导致ΔKth很小，这里偏安全地取为零.2区为裂纹稳定扩展区，是疲劳寿命的重要组成部分.对于该阶段疲劳寿命的计算，工程上应用最广泛的是Paris公式：

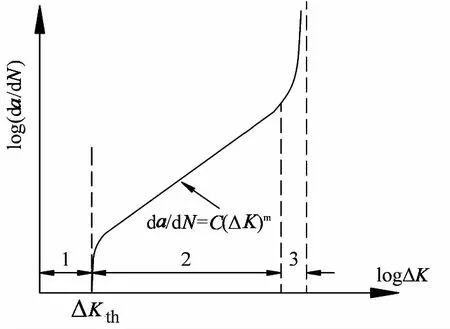
图8　da/dN-δK曲线

da/dN=C(δK)m.

(5)

式中：C，m为裂纹扩展性能的基本参数，根据文献[6]，取C=1.58×10-11(m/周)，m=2.67；ΔK为应力强度因子幅值，是裂纹扩展的主要控制参量.ΔK可按式(6)进行计算[13]：

(6)

式中：fe，fs，ft，fg分别为裂纹形状、自由表面、有限板厚、应力集中修正系数，按下式计算[14]：

(7)

式中：a，c分别为裂纹深度和半长度，且a/c=0.1；t为板厚，h，θ分别为焊缝高度和角度.计算得到各典型细节的δK如图9所示.

从图9可以看出，典型构造细节应力强度因子的数值随着裂纹尺寸的增大而增大，且增大速率越来越快，这是因为裂纹尺寸越大，材料净截面积越小，

裂纹扩展所受约束越小，越有利于裂纹的扩展.

各构造细节的疲劳寿命可按式(8)计算：

(8)

由式(7)可知f(a)的取值与裂纹尺寸有关，因此为计算式(8)，先回归分析得到δK与裂纹尺寸a之间的关系式，代入式(8)即可得到各典型细节的疲劳寿命，计算结果见表3.

裂纹尺寸/mm

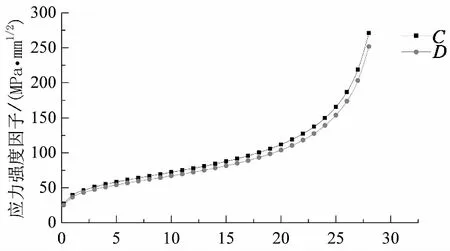
裂纹尺寸/mm

构造细节应力脉/MPa初始裂纹/mm临界裂纹/mm等效应力强度因子疲劳寿命/年A11.660.250ΔK=0.0147a3-0.892a2+15.528a+24.79135.1B10.730.250ΔK=0.0135a3-0.763a2+14.295a+22.82160.6C9.480.230ΔK=0.0153a3-0.447a2+6.716a+32.482197.9D8.710.230ΔK=0.0142a3-0.415a2+6.224a+30.103242.2

6.2损伤容限设计

损伤容限设计是20世纪70年代发展并被大量使用的抗疲劳设计方法.该方法的思路是：假定构件存在初始裂纹，用断裂力学方法对其剩余疲劳寿命和裂纹扩展速率进行评估，建立完善的检测方案，当裂纹尺寸达到预期尺寸时，对构件加以维修或更换，以保证结构的安全.设计原理如图10所示.

图11为各构造细节对应的裂纹扩展曲线，从图可看出，使用初期裂纹扩展很慢，构件大部分疲劳寿命消耗在此阶段，当裂纹尺寸达到10 mm时，各构造细节已消耗了疲劳寿命的61.2%～79.3%.因此在进行损伤容限设计时，可预设裂纹尺寸为10 mm，当检查到裂纹达到10 mm时，及时对锚拉板加以维修或更换.

图10　损伤容限设计原理

使用寿命/年

使用寿命/年

7　结　论

1)对于锚拉板结构，其锚筒与锚拉板的双面单V形焊缝以及锚拉板与主梁焊缝是重要承载焊缝，焊缝端点处由于几何形状的突变存在严重应力集中现象，是疲劳评估中的关键构造细节.

2)建立了基于断裂力学的锚拉板疲劳寿命分析方法，得到锚拉板各典型细节的疲劳寿命均超过100年，说明锚拉板具有很好的抗疲劳性能，可在今后的设计中加以推广.

3)锚拉板裂纹初期的扩展速率很慢；当出现肉眼可见的裂纹时(如10 mm)，已消耗了60%以上的疲劳寿命，基于损伤容限设计，取10 mm为裂纹维修点.

本文采用经典公式来计算应力强度因子，如何建立三维实体断裂力学模型、用有限元方法计算应力强度因子有待进一步研究.

[1]李小珍,蔡婧.大跨度钢箱梁斜拉桥索梁锚固结构型式的比较研究[J].土木工程学报，2004，37(3)：73-79.

LI Xiao-zhen,CAI Jing,Study on models of cable-girder anchorage for long-span cable-stayed bridges with steel box girder[J].China Civil Engineering Journal，2004,37(3):73-79.(In Chinese)

[2]满洪高.大跨度钢斜拉桥索梁锚固结构试验研究[D].成都：西南交通大学土木工程学院，2007：1-2.

MAN Hong-gao.Experimental studies on cable-girder anchorage for long-span cable-stayed bridges with steel girder[D].Chengdu: College of Civil Engineering，Southwest Jiaotong University,2007：1-2.(In Chinese)

[3]祝志文，钱六五.基于有效缺口应力法的正交异性钢桥面板疲劳评价[J].湖南大学学报:自然科学版,2015，42(9)：59-67.

ZHU Zhi-wen，QIAN Liu-wu.Fatigue assessment of orthotropic steel bridge deck based on the effective notch stress method[J].Journal of Hunan University: Natural Sciences,2015，42(9)：59-67.(In Chinese)

[4]FISHER J W.Fatigue and fracture in steel bridges[M].New York：Wiley and Sons，Inc，1984:1608-1623.

[5]王元清，张元元.钢厚板母材及其焊接影响区的Z向拉伸试验[J].湖南大学学报:自然科学版,2014，41(2)：26-31.

WANG Yuan-qing,ZHANG Yuan-yuan.Experimental research of the z-direction tensile properties of thick plate steel and its heat affected zone[J].Journal of Hunan University: Natural Sciences,2014，41(2)：26-31.(In Chinese)

[6]宗亮，施刚，王元清,等.Q345qD桥梁钢疲劳裂纹扩展速率试验研究[J].中国铁道科学,2015，36(3)：37-44.

ZONG Liang,SHI Gang,WANG Yuan-qing,et al.Experimental studies on fatigue crack growth rate of Q345qD type bridge steel[J].China Railway Science,2015，36(3)：37-44.(In Chinese)

[7]彭鲲，李立峰.波形钢腹板组合箱梁疲劳性能试验与理论分析[J].中国公路学报,2013，26(4)：94-101.

PENG Kun,LI Li-feng.Experimental and theoretical analysis on fatigue performance of composite box girder with corrugated webs[J].China Journal of Highway and Transport,2013,26(4)：94-101.(In Chinese)

[8]王春生，陈艾荣，陈惟珍.基于断裂力学的老龄钢桥剩余寿命与使用安全评估[J].中国公路学报,2006，19(2)：42-48.

WANG Chun-sheng,CHEN Ai-rong,CHEN Wei-zhen.Assessment of remaining fatigue life and service safety for old steel bridges based on fracture mechanics[J].China Journal of Highway and Transport,2006,19(2)：42-48.(In Chinese)

[9]童乐为，顾敏.基于断裂力学的圆钢管混凝土T型焊接节点疲劳寿命预测[J].工程力学,2013，30(4)：331-337.

TONG Le-wei,GU Min.Prediction of fatigue life for welded T-joints of concrete-filled circular hollow sections based on fracture mechanics[J].Engineering Mechanics,2013，30(4)：331-337.(In Chinese)

[10]JTG D60-2015 公路桥涵设计通用规范[S].北京：人民交通出版社，2015:31-63.

JTG D60-2015 General specification for design of highway bridges and culverts[S].Beijing：China Communications Press，2015:31-63.(In Chinese)

[11]陈传尧.疲劳与断裂[M].武汉：华中科技大学出版社，2001：3-151.

CHEN Chuan-yao.Fatigue and fracture[M].Wuhan: Huazhong University of Science and Technology Press,2001:3-151.(In Chinese)

[12]中国航空研究院.应力强度因子手册[M].北京：科学出版社，1993：375-384.

China Aviation Academy.Stress intensity factor handbook[M].Beijing：Science Press,1993:375-384.(In Chinese)

[13]ALBRECHT P，YAMADA K.Rapid calculation of stress intensity factors[J].Journal of the Structural Division，ASCE，1977,103(2):377-389.

[14]王应良.基于抵抗疲劳和断裂的桥梁允许最大钢板厚度的确定[J].土木工程学报，2012，45(10)：145-151.

WANG Ying-liang.Permissible maximum plate thickness assessment of steel bridges based on resistance fatigue and fracture[J].China Civil Engineering Journal,2012,45(10):145-151.(In Chinese)

Assessment of Fatigue Life for Anchor Plates Based on Fracture Mechanics

LI Li-feng†,TANG Wu,TANG Jin-liang

(College of Civil Engineering,Hunan Univ,Changsha,Hunan410082,China)

To investigate the fatigue performance of anchor plates,a composite beam cable-stayed bridge was taken for example in this study.A loading model in the new standard for steel bridge and the rain-flow method were applied to gain fatigue load spectrum,combined with a three dimensional finite element model to identify the typical structural details and fatigue stress spectrum of anchor plates.Initial surface cracks were imported in the typical details,and stress intensity factors of crack tips were calculated.The stress intensity factor and crack size were regressed by substituting in Paris formula,which were integrated to gain the fatigue life of typical structural details.The assessment of fatigue life for anchor plates based on fracture mechanics was then established.The results show that the fatigue life for anchor plate based on fracture mechanics is over 100 years,satisfying the requirement of design and utilization; the crack is developed very slowly in the early time,but when it reaches 10 millimeters,50% to 80 % of its fatigue life is consumed.Therefore,reinforcement should be timely applied to the anchor plates.

fracture mechanics; anchor plate; fatigue life; stress intensity factor; Paris formula

1674-2974(2016)09-0082-06

2015-10-25

国家自然科学基金资助项目(51278183),National Natural Science Foundation of China(51278183); 贵州省交通厅科研课题(201412202)；交通运输部建设科技项目“大跨径钢桁加劲梁悬索桥关键技术研究”(2013318798320)；湖南省交通科技项目(201219)

李立峰(1971-)，男，湖南沅江人，湖南大学教授，博士

†通讯联系人，E-mail:lilifeng@hnu.edu.cn

U441.4

A