一种比例再保险和投资最优化问题*

曾敏 陈萍

（南京理工大学理学院，南京，210094）

一种比例再保险和投资最优化问题*

曾敏 陈萍

（南京理工大学理学院，南京，210094）

假设保险盈余服从跳跃扩散过程，保险资金投资标的包括无风险资产和风险资产两部分，其中股票价格过程服从CEV模型.本文研究了一种终值财富期望指数效用最大化的最优化比例再保险投资问题.利用随机控制理论技术，得到比例再保险投资过程的HJB方程，并从理论上推导出了最优投资策略和价值函数的显示表达式.

比例再保险 CEV模型 指数效用函数 随机控制理论 HJB方程

HJB equation

1　引言

保险公司的两大核心业务是承保业务和投资业务，承保业务是主要的聚集资金渠道，也是利润的重要来源，随着保险业务的发展，保险投资业务越来越受重视，同时也成为创造盈利的重要途径.但是保险资金投资与一般的资金运用具有很大的差别，根据《保险法》规定，“保险公司的资金运用必须稳健，遵循安全性原则，以保证资金的保值增值”，保险公司资金投资再寻求最大收益的同时，必须履行随时赔偿损失和给付保险金的义务.而比例再保险和资金投资作为分散风险和创造利润的有效途径，在实务中也具有重要的现实意义.再保险决策不仅包括选择再保险的种类，更重要的是根据公司的偿付能力及公司经营者所持的风险态度，从中决定公司的自留额及相应的再保险金额.

在现有的文献研究中，依据保险人采用的目标函数不同，比例再保险和投资问题可以大致分为两大类，一类以保险人破产概率最小化为目的，一类以期终财富预期效用最大化为目的.同时，文献研究中一般定义保险人盈余过程为复合泊松过程或者带有漂移项的布朗运动. Browne［1］假设盈余过程服从带漂移的布朗运动，最早研究了破产概率最小化目标下的最优化再保险和投资问题；Hipp［2］假设盈余过程为复合泊松过程，研究了破产概率最小化目标下的最优化再保险和投资问题；Hipp［3］利用Lundberg-Cramer条件描述了盈余过程，在破产概率最小化目标和资金仅投资于风险资产双重条件下，当索赔过程服从指数分布时，推导出了最优化策略的显示表达式；假设盈余过程服从复合泊松过程时，Liu和Yang［4］以及Yang和Zhang［5］利用数值方法，讨论了最优投资策略，并且求解了最小破产概率.在目标函数确定为期终财富预期效用最大化时，依据对盈余过程的描述，Browne［1］以几何布朗运动为例，Yang和Zhang［5］以复合泊松过程为例，Fernadez［6］以纯跳跃过程为例，分别研究了最优投资问题，并求解出了相应的显示表达式.

上述文献研究中，有一个共同的特征是，均假设风险资产价格服从几何布朗运动即GSM模型，该模型假设价格波动率为常数.但是现实中，风险资产价格波动率常常出现偏斜现象，即实际的波动率通常与标的资产的价格相关，并不是恒定不变的.而CEV模型下标的资产的波动率正好满足偏斜要求，这一点更符合现实的金融市场，对于几何布朗运动的假定是一个更好的改进.

CEV模型对于几何布朗运动的一个自然补充，陈萍和冯予［7］归纳了该模型的相关性质，并研究了模型的参数估计和相应的轨道模拟.CEV模型通常用于期权定价分析，Xiao［8］应用CEV模型于养老金投资模型，并利用Legendre变换和对偶理论推导出了对数指数效用的对偶解.Liang［9］研究了基于CEV模型的期终财富预期指数效用最大化的再保险投资问题，并利用随机控制技术，推导出了最优策略和值函数的显示解，同时通过数值例子说明了最优策略中模型参数的影响.Zhu［10］研究了有违约风险的保险人最优比例再保险和投资问题，在再保险费率满足指数形式假设条件下，推导出了最优策略.

类似于经典的投资理论马科维茨均值-方差投资组合选择问题，在本文中，受Xiao［8］，Liang［9］和Zhu［10］研究内容的启发，假设保险盈余过程服从跳扩散风险模型，理赔过程服从复合泊松过程，同时再保险保费函数呈现指数形式，以期终财富预期指数效用最大化为目标，建立基于CEV模型的再保险和投资模型，利用随机控制理论技术，推导出了最优策略和值函数的显示解.

2　模型假设与构建

假设保险人的盈余过程xt服从跳-扩散模型：

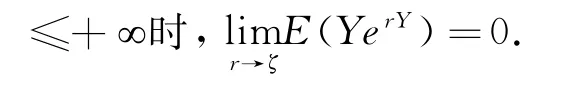
Liang［11］在研究带有违约风险的最优化再保险和投资问题一文中，详细阐述了再保险费率满足指数形式的合理性，受此启发，本文假设再保险费率c（qt）为指数函数，具体形式为c（qt）=α0-1log E（eα0S）=α0-1λ（MX（α0（1-q（t）））-1），其中，α0＞0表明分保人的风险厌恶特点.

保险人可以通过建立再保险合约分散风险，在《保险法》的监管要求下，保险人可以将全部的保险盈余投资于金融市场中，本文为了简化模型，保险盈余投资标的中仅包含一种风险资产（以股票为例）和一种无风险资产（以债券为例）.在经典的投资组合理论中，无风险资产的价格Rt过程满足微分方程：

其中r＞0为无风险利率.

风险资产的价格St过程满足GSM模型，即：

其中μ＞r，σ＞0，Wt｛｝t≥0为标准布朗运动，μ-r＞0表示风险资产相对无风险资产具有的风险溢价.

由于现实的金融市场中，风险资产价格波动率常常呈现偏斜现象，本文假定风险资产价格过程满足CEV模型，CEV模型的波动率不再是常数，代替为与资产价格相关的随机波动率. CEV模型的微分方程为：

其中，β为常数.

在CEV模型中，假定波动率弹性为常数，记β为方差弹性因子.当β=1时，弹性为0，股票价格服从对数正态分布，对应几何布朗运动模型；当β=1/2时，弹性为-1，模型的波动项与CIR模型相同.弹性因子β是决定价格与收益的波动率之间关系的关键指标，如果β＞1，显示价格与波动率之间呈现正相关关系，即价格越高，收益的波动率越大.当0＜β＜1时，显示价格与波动率之间呈现负相关关系，即价格越高，收益的波动率反而越小.

本文假定交易过程可以连续进行，所有资产都可以无限划分，同时允许卖空，不考虑交易成本.记Xt｛｝t≥0为保险盈余过程，其中，Xt表示保险人在时刻t的财富价值，πt表示保险人在投资策略π 下时刻t投资的风险资产价值，则（Xt-πt）表示无风险资产价值.由此，可以建立保险人在时刻t的财富方程为：

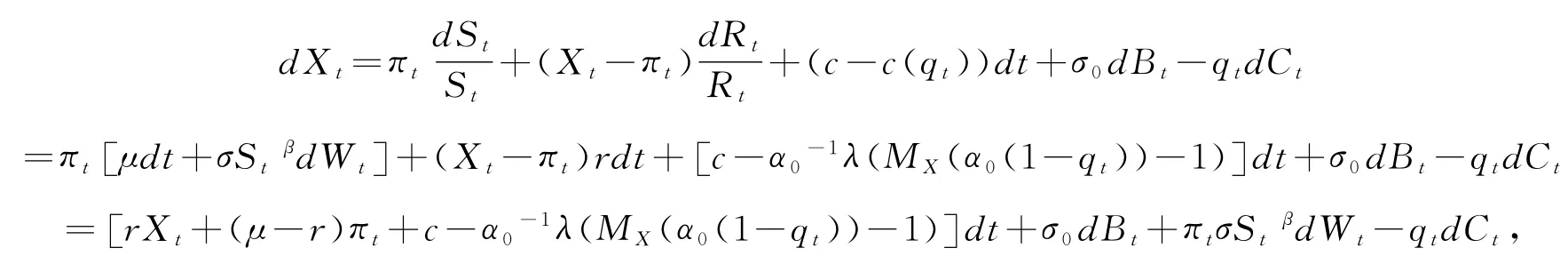
其中，

3　模型求解

为了求解问题（5），定义值函数V（t，x，s）为，

值函数V（t，x，s）满足如下HJB方程

其中，V（T，x，s）=u（x）.

依据随机控制理论，如果求出了（6）式的值函数V（t，x，s），即找到了（5）式的最优解，从而确定再保险和投资最优策略（π*，q*）.

依据Browne［1］，Xiao［8］，Liang［9］，Zhu［10］的研究成果，假定值函数的形式为，

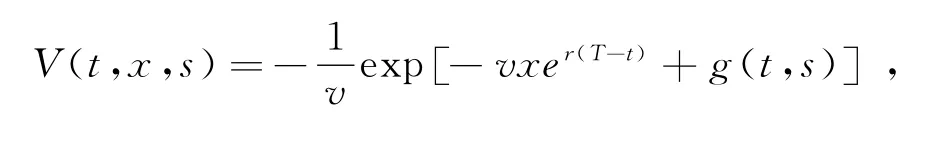
其中g（T，s）=0.

进一步有，

Vt，Vx，Vxx，Vs，Vss，Vxs分别为值函数V（t，x，s）的一阶或二阶偏导数，代入（7）式得，

进一步，上式可简化为

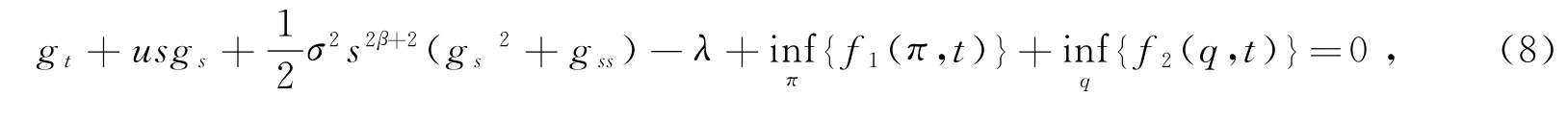
其中f1（π，t），f2（q，t）分别为

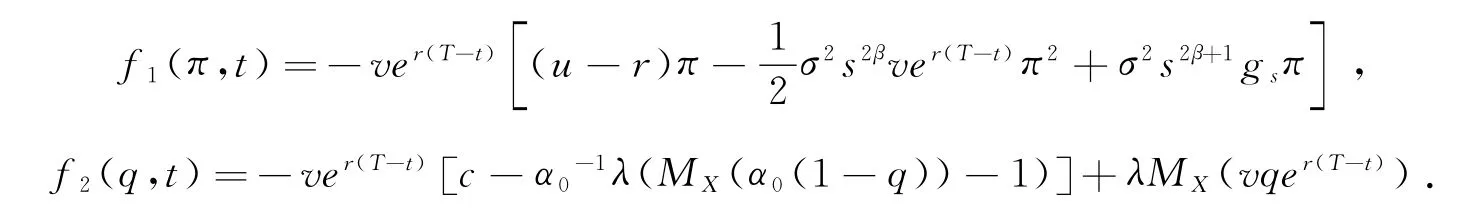
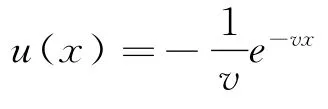
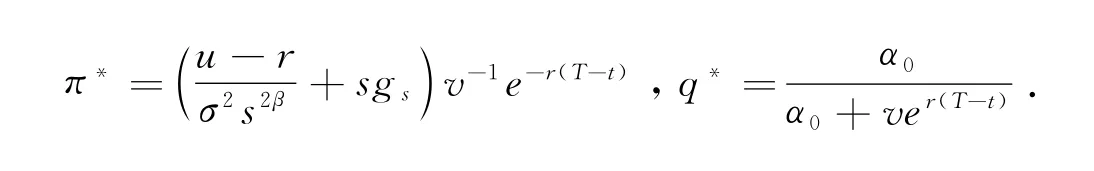
证明 由值函数的HJB方程可知

其中，

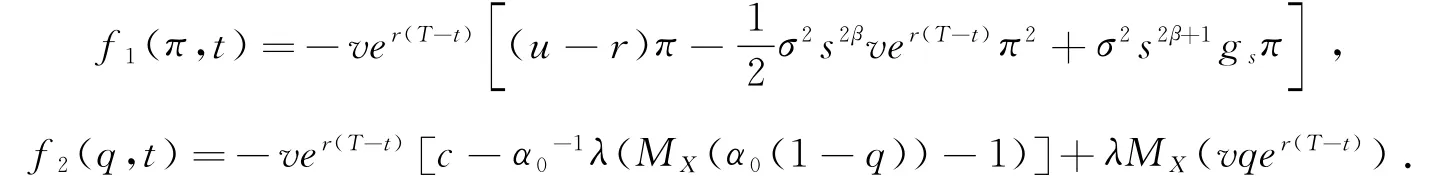
分别求函数f1（π，t）=O1（π），f2（q，t）=O2（q）的极值点，则对应的解（π*，q*）即为所寻找的再保险和投资最优策略.

再令O2′（q）=0，得

即α0（1-q）=vqer（T-t）.

所以求得保险人保留比例为，

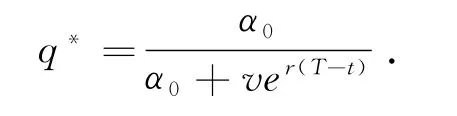
定理得证.

利用所求得的最优策略（π*，q*），可推出保险人在最优策略下的值函数的显示表达式.

将所求得的π*代入f1（π，t）有

（8）式进一步转化为

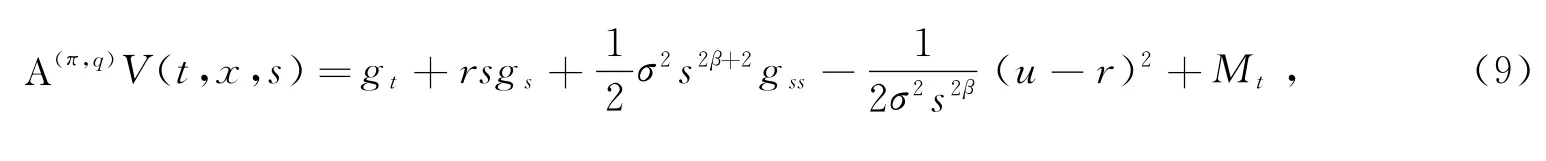
不妨假设g（t，s）=h（t，y）=l（t）y+Z（t），y=s-2β.

由此，（9）式转化为

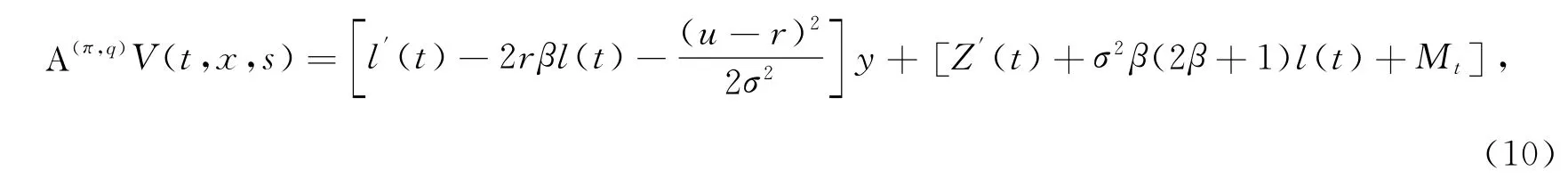
其中，l（T）=Z（T）=0.

令A（π，q）V（t，x，s）=0，则方程（10）式等价于带有边界条件的两个方程，如下所示：

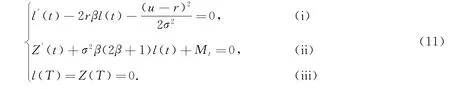
由（i），（iii）式可求得，

由（ii），（iii）式可求得，

其中，

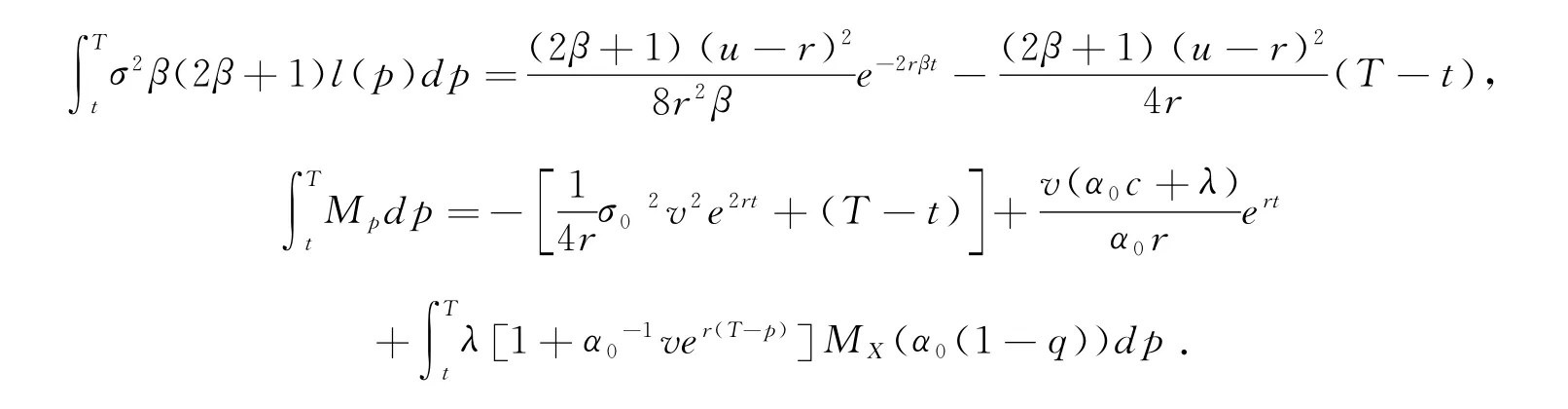
将（12），（13）式代入值函数，即可得显示表达式为

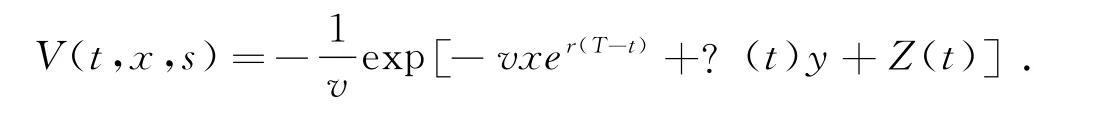
4　结论

在本文中，投资标的仅考虑一种无风险资产和一种风险资产，其中风险资产价格服从CEV模型，保险人盈余过程服从跳扩散过程，并假设两者布朗运动相互独立.本文以保险人期终财富预期效用最大化为目标建立再保险和投资模型，在模型中，效用函数和再保费率函数均选定为指数形式，依据最优化原理，建立相应的HJB方程，利用随机控制理论技术对模型求得了显示解.

为了简化模型，本文的假设条件比较多，只对再保险和投资问题进行了初步研究，如果将条件放宽，例如可以考虑多种风险资产或者布朗运动之间不再相互独立的情形，还需要进一步深入研究.

［1］Browne S.Optimal investment policies for a firm with random risk process：exponential utility and minimizing the probability of ruin［J］.Mathematics of Operations Research，1995，20：937-958.

［2］Hipp C，Taskar M.Stochastic control or optimal new business［J］.Insurance：Mathematics and Economics，2000，26：185-192.

［3］Hipp C，Plum M.Optimal investment for insurers［J］.Insurance：Mathematics and Economics，2000，27：215 -228.

［4］Liu C，Yang H.Optimal investment for a insurer to minimize its probability of ruin［J］.North American Actuarial Journal，2004，8：11-31.

［5］Yang H，Zhang L.Optimal investment for insurer with jump-diffusion risk process［J］.Insurance：Mathematics and Economics，2005，37：615-634.

［6］Fernandez B.An optimal investment strategy with maximal risk aversion and its ruin probability［J］.Mathematical Methods of Operations Research，2008，68：159-179.

［7］陈萍，冯予，赵慧秀，蔡井伟.连续时间金融模型的非参数统计分析［M］.北京：科学出版社，2014：40-43.

［8］Xiao J，Zhai H，Qin C.The constant elasticity of variance model and the Legendre transform-dual solution for annuity contracts［J］.Insurance：Mathematical and Economics 2007，40：302-310.

［9］Liang Z，Yuen K，Cheung，K.Optima reinsurance-investment problem in a constant elasticity of variance stock market for jump-diffusion risk model［J］.Stochastic Models 2012，28：585-597.

［10］Zhu H，Deng C.Optimal reinsurance and investment problem for an insurer with counter-party risk［J］. Insurance：Mathematics and Economics 2015，61：242-254.

A Proportional Reinsurance and Investment Optimization Problem

Zeng Min Chen Ping
（College of Science，Nanjing University of Science and Technology，Nanjing 210094，China）

In this paper，insurance surplus are assumed to be jump-diffusion process，insurance funds portfolio includes risk-free asset and risk assets，the stock price process follows the CEV model.We study a kind of optimal investment-reinsurance problem of maximizing the expected exponential utility of terminal wealth. Using the theory of stochastic control technology，get the HJB equation of proportional reinsurance investment process，and deduce the expression of the optimal investment strategy and value function in theory.

Proportional reinsurance CEV model Exponential utility function Stochastic control theory

2016年05月06日