内置式永磁电机齿槽转矩的优化设计

黄燕涛， 郭新华,2， 项雷军

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 香港理工大学 电气工程学院， 中国 香港特别行政区)



内置式永磁电机齿槽转矩的优化设计

黄燕涛1， 郭新华1,2， 项雷军1

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 香港理工大学 电气工程学院， 中国 香港特别行政区)

针对内置式永磁同步电机存在的齿槽转矩问题，采用有限元软件Maxwell分别对不同分段数、不同非均匀气隙情况下的内置式永磁同步电机进行分析.理论分析表明：转子分段斜极可以抑制齿谐波，从而削弱齿槽转矩；而采用非均匀气隙结构则可以通过优化气隙磁密的特定次谐波削弱齿槽转矩.依据理论分析，提出一种二者相结合的方法抑制电机的齿槽转矩.优化结果表明：该方法能有效地抑制电机的齿槽转矩.

内置式永磁同步电机； 齿槽转矩； 转子分段斜极； 非均匀气隙

由于内置式永磁同步电机(IPMSM)高效率、高功率密度等优点，在电动汽车、航天航空、机器人、工业控制等高性能领域得到广泛地应用[1-2].然而，在永磁电机中，转子永磁体和定子齿槽相互作用，不可避免地产生齿槽转矩，导致转矩波动，引起振动和噪声，从而影响系统的控制精度[3-4].因此，如何削弱电机齿槽转矩是高性能永磁电机的重要研究内容.近年来，国内外学者对电机齿槽转矩的影响因素和削弱进行了研究，提出很多有效的方法.文献[5-9]通过解析法，分析了定子槽宽、槽口偏移、转子永磁体分块、磁极偏移、磁极不对称分布和极弧系数对齿槽转矩的影响；文献[10-12]通过分析电机气隙磁场分布，研究了气隙磁场对齿槽转矩的影响.但是,关于电机齿槽转矩的研究大多是针对表面式永磁同步电机，而针对内置式永磁同步电机的研究较少.本文利用有限元分析软件Maxwell分析转子分段数和采用非均匀气隙磁密结构对内置式永磁同步电机齿槽转矩的影响，通过改变转子结构偏心距离和转子分段斜极两种优化方法，结合仿真结果得到有效削弱电机齿槽转矩的方案.

1　齿槽转矩基本原理及电机模型

1.1基本原理

齿槽转矩是永磁电机绕组不通电时，永磁体和电枢齿槽之间相互作用产生的转矩[13]，可定义为

(1)

式(1)中：W为电机不通电时的磁场能量；α为定转子相对位置角.

假设电枢铁心的磁导率为无穷大，则电机内存储磁场能量[13-14]近似为

(2)

式(2)中：μ0为气隙磁导率；V为气隙体积；Br(θ)为永磁体剩磁；hm(θ)为永磁体充磁方向长度沿圆周方向的分布；δ(θ,α)为有效气隙长度.

(3)

(4)

将式(2)～(4)代入式(1),得到不考虑斜槽情况下的齿槽转矩表达式,即

(5)

式(5)中：La为电枢铁心的轴向长度；R1和R2分别是电枢外半径和定子轭内半径；n为使nz/(2p)为正整数的整数.

图1　IPMSM模型Fig.1　Model of IPMSM

1.2电机模型

利用Maxwell有限元分析软件建立电机模型，模型截面如图1所示.电机的主要参数如下：额定功率4 kW；额定电压540 V;极对数8;定子槽数48;额定转速1 200 r·min-1;定子铁心外径180 mm；定子铁心内径115.4 mm；转子外径114 mm；转子内径45 mm.

2　分段斜极对齿槽转矩的影响

2.1斜极方法

(a) 转子连续斜极　　　　　　(b) 转子分段斜极图2　永磁磁极Fig.2　Permanent magnetic pole

转子斜极与定子斜槽的原理相同[15]，其方法有2种，如图2所示.采用连续斜极的效果和定子斜槽基本一致，但该方法会增大工艺操作难度，提高电机生产成本，不利于大批量生产.采用转子分段斜极的方法不仅能够有效地削弱电机齿槽转矩，而且操作工艺相对简单，有利于降低电机生产成本.所以,文中采用转子分段斜极的方法.

2.2斜极角度

在整数槽电机中，存在高次谐波磁动势.其中,有一种v=(z/p)±1次的高次谐波称为一阶齿谐波，该谐波的次数与一对极下的齿数z/p有特定关系[15].当转子分为N段时，为了更好地削弱齿谐波和齿槽转矩，应使每一段分段转子对应的z/p次谐波的矢量和为零.

由于z/p次谐波在一个定子齿距内的电角度为360°,若要较好地削弱齿谐波和齿槽转矩，则N个矢量在360°电角度方位内均匀分布，即N段转子在一个定子齿距范围内等间距错开.假设相邻两段转子之间沿圆周分布错开(1/N)·θτ(θτ为齿距角度)，相对于第1段转子，第N段转子错开角度为[(N-1)/N]·θτ，则斜极角度θPM与分段数N的关系为

(6)

2.3不同分段数的有限元分析

采用8极48槽电机，根据式(6)可得：当转子分2段式,斜极角为3.75°；当转子分3段式,斜极角为5°；当转子分4段式,斜极角为5.625°.有限元仿真得到的齿槽转矩及其谐波分析结果，如图3,4所示.图3,4中：Tcog为齿槽转矩；t为时间；N为分段数;n为谐波次数；M为转矩谐波幅值.

由图3，4可知：采用转子分段斜极能够较好地削弱齿槽转矩，并且齿槽转矩幅值随着分段数的增大而减小;不分段时，齿槽转矩中存在较大的2,4次谐波分量;当分段数N=2时，齿槽转矩中的2次谐波分量被大幅度削弱，而在其他高次谐波中4次谐波分量较大;当分段数N=3时，齿槽转矩被大幅度削弱，其中6次谐波分量较大;当分段数N=4时，齿槽转矩幅值和N=3时的齿槽转矩幅值相比减小不多，其谐波含量中,8次谐波含量较大.

图3　不同分段数时的齿槽转矩Fig.3　Cogging torque in different segments

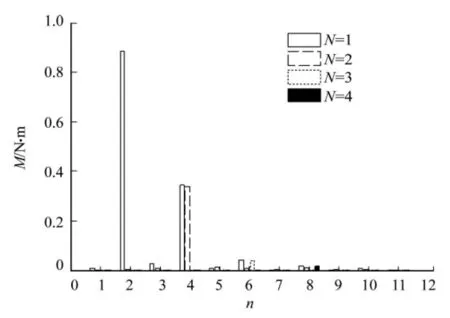
图4　不同分段数时齿槽转矩的谐波分析Fig.4　Harmonic analysis of cogging torque in different segments

3　非均匀气隙磁密对齿槽转矩的影响

由式(5)可得：当R1,R2,La等参数一定时，齿槽转矩幅值与Br，nz/(2p)有关.在有限元分析软件Maxwell中，齿槽转矩的取值为电机不通电时在瞬态场下计算得到的转矩值.该情况下,空载气隙磁密与永磁体剩磁有关，因此,只需减小空载气隙磁密的nz/(2p)次谐波含量，便可削弱齿槽转矩.文中采用8级48槽内置式永磁同步电机，其中,空载气隙磁密的6n次谐波分量会影响电机齿槽转矩的幅值.

3.1基本原理

在均匀气隙磁密的IPMSM中，转子是一个标准的圆周，转子外圆周与定子内圆周是同心圆.为了优化气隙磁密波形，电机转子采用非均匀气隙结构，如图5所示.图5中:O为原转子外圆圆心;O′为一个极距范围内优化转子外圆圆心;OO′为优化转子的偏心距h；右半图中虚线部分为优化后的转子外沿.

3.2不同偏心距的有限元分析

为了研究不同偏心距h对电机空载气隙磁密和齿槽转矩的影响，选取了10个不同的偏心距离，从0开始以1mm长度递增，对电机进行有限元分析，并对结果进行傅里叶分解，得到相应的空气隙磁密特定次谐波含量和齿槽转矩波形.其中，不同偏心距的空载气隙磁密6,12,18次谐波含量，如表1所示.不同偏心距的齿槽转矩波形，如图6所示.

图5　内置式永磁同步电机非均匀气隙结构图Fig.5　Non-uniform air gap structure diagram of IPMSM

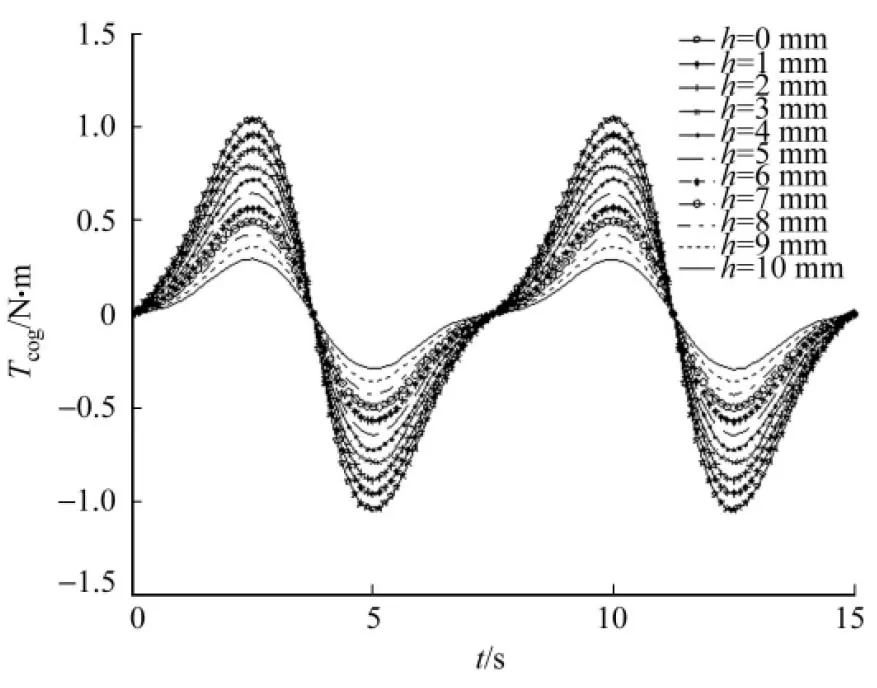
图6　不同偏心距的齿槽转矩Fig.6　Cogging torque under different eccentric distance

表1　不同偏心距的空载气隙磁密6,12,18次谐波含量

图7　优化前后电机齿槽转矩Fig.7　Contrast of cogging torque before and after optimization

图8　优化前后空载气隙磁密Fig.8　No-load gap flux density before and after optimization

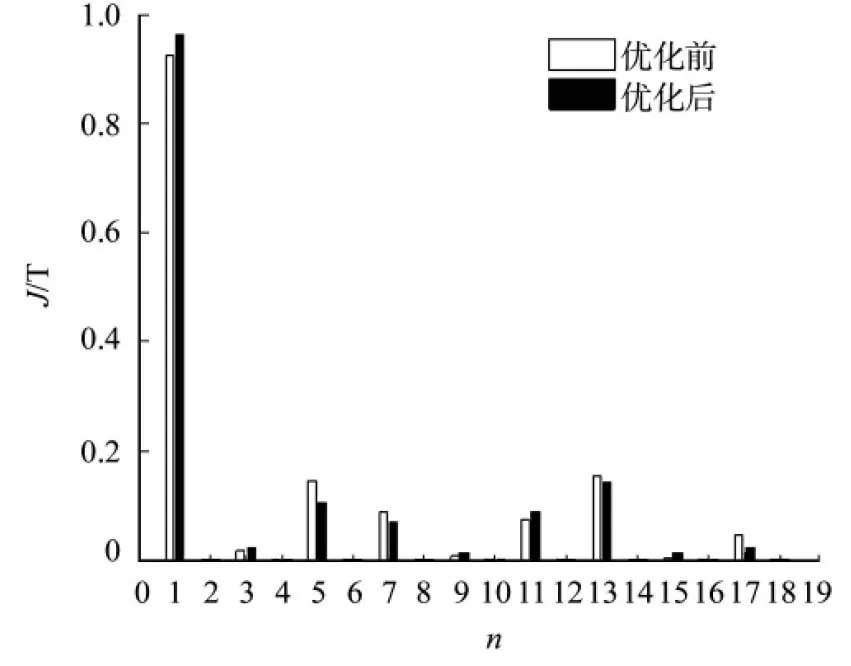
图9　优化前后空载气隙磁密的谐波分析Fig.8　No-load gap flux density before Fig.9　Harmonic analysis of no-load gap flux density before and after optimization

由表1可知：随着偏心距的增加，空载气隙磁密6,12,18次的谐波含量在不断减少.由图6可知：电机齿槽转矩的大小随偏心距的增大而减小.因此，采用非均匀气隙结构能降低空载气隙磁密6n次谐波含量，且空载气隙磁密的6n次谐波分量对电机齿槽转矩的幅值有影响，即转子采用非均匀气隙结构可有效地削弱电机齿槽转矩.但是，随着偏心距的增加，电机转子的制造工艺难度也随之增大.所以,应在制造工艺所允许的基础上选取适合的偏心距.

4　优化结果

结合以上分析结果，同时考虑工艺操作的问题，选取电机转子磁极分段数N=3，转子偏心距h=10 mm，仿真结果如图7～9所示.图8，9中：B为空载气隙磁密；α为机械角度；n为谐波次数；J为磁密谐波幅值.

由图7可知:优化后，电机齿槽转矩被大大削弱.由图8,9可知:优化后，空载气隙磁密的正弦畸变率为35.22%，与优化前的37.59%相比有所降低，优化后的气隙磁密各谐波含量明显减少，且空载气隙磁密波形得到优化，波形接近正弦分布.

5　结束语

基于解析法对齿槽转矩进行理论分析，给出转子分段数和斜极角之间的关系及电机空载气隙磁密与齿槽转矩的关系.利用有限元分析软件Maxwell,对转子分段斜极和采用非均匀气隙磁密结构的内置式永磁电机的齿槽转矩进行仿真分析.结合以上2种方法，得到齿槽转矩最小的优化方案.仿真结果表明:该方法能够有效地优化电机空载气隙磁密波形且削弱齿谐波，从而抑制电机齿槽转矩.

[1]夏永洪,黄劭刚.齿谐波绕组电流对电枢绕组空载电压波形的影响[J].中国电机工程学报,2014,34(6):910-916.

[2]彭兵,夏加宽,董婷,等.不等齿宽提高多槽少极隔齿隔相绕组永磁电机转矩的方法[J].中国电机工程学报,2012,32(增刊1):242-248.

[3]FAZIL M,RAJAGOPAL K R.A novel air-gap profile of single-phase permanent-magnet brushless DC motor for starting torque improvement and cogging torque reduction[J].IEEE Transactions on Magnetics,2010,46(11):3928-3932.

[4]罗宏浩,廖自力.永磁电机齿槽转矩的谐波分析与最小化设计[J].电机与控制学报,2010,14(4):36-40.

[5]王晓远,贾旭.基于槽口优化的电动汽车用大功率无刷直流电机齿槽转矩削弱方法[J].电工技术学报,2013,28(6):40-45.

[6]杨玉波,王秀和,朱常青.基于分块永磁磁极的永磁电机齿槽转矩削弱方法[J].电工技术学报,2012(3):73-78.

[7]LIU Ting,HUANG Shoudao,GAO Jian.A method for reducing cogging torque by magnet shifting in permanent magnet machines[C]∥International Conference on Electrical Machines and Systems.Incheon:IEEE Press,2010:1073-1076.

[8]王道涵,王秀和,丁婷婷,等.基于磁极不对称角度优化的内置式永磁无刷直流电动机齿槽转矩削弱方法[J].中国电机工程学报,2008,28(9):66-70.

[9]杨玉波,王秀和,丁婷婷.基于单一磁极宽度变化的内置式永磁同步电动机齿槽转矩削弱方法[J].电工技术学报,2009,24(7):41-45.

[10]DUTTA R,SAYEEF S,RAHMAN M F.Analysis of cogging torque and its effect on direct torque control (DTC) in a segmented interior permanent magnet machine[C]∥Power Electronics Specialists Conference.Orlando:IEEE Press,2007:2568-2574.

[11]KIM T W,CHANG J H.Effective step-skew method for cogging torque reduction in surface-mounted permanent magnet synchronous motor[J].Journal of the Korean Physical Society,2013,63(3):288-292.

[12]AXAR Z,ZHU Z Q,OMBACH G.Influence of electric loading and magnetic saturation on cogging torque, back-EMF and torque ripple of PM machines[J].IEEE Transactions on Magnetics,2012,48(10):2650-2658.

[13]王秀和.永磁电机[M].北京:中国电力出版社,2010:71-115.

[14]WANG Xiuhe,YANG Yubo,FU Dajin.Study of cogging torque in surface-mounted permanent magnet motors with energy method[J].Journal of Magnetism and Magnetic Materials,2003,267(1):80-85.

[15]汤蕴缪.电机学[M].北京:机械工业出版社,2011:143-147.

(责任编辑： 黄晓楠英文审校： 崔长彩)

Optimal Design of Cogging Torque of Interior Permanent Magnet Motor

HUANG Yantao1, GUO Xinhua1,2, XIANG Leijun1

(1. College of Information Science and Engineering, Huaqiao University, Xiamen 361021, China;2. Department of Electrical Engineering, The Hong Kong Polytechnic University, Hong Kong SAR, China)

In order to solve the issues on cogging torque of interior permanent magnet synchronous motor (IPMSM), the IPMSMs with different segments and non-uniform air gap were analyzed using the finite element software Maxwell in this paper. Theoretical analysis showed that teeth harmonics can be effectively reduced by step skewing of rotor, which leads to the decrease of cogging torque; meanwhile, the cogging torque can also be minimized by introducing the non-uniform air gap based on specific harmonic of optimal gap flux density. On the basis of the theory analysis, a combined method is proposed to eliminate the cogging torque of IPMSM. Optimization results verify the described method can effectively reduce the cogging torque of the IPMSM.

interior permanent magnet synchronous motor; cogging torque; step skewing of rotor; non-uniform air gap

10.11830/ISSN.1000-5013.201605003

2015-07-28

郭新华(1977-)，男，副教授，博士，主要从事永磁型双机械端口电机、永磁同步电机、多相电机的驱动控制,中压大功率永磁(异步)牵引系统控制的研究.E-mail:guoxinhua@hqu.edu.cn.

国家自然科学基金资助项目(51477058)； 福建省自然科学基金资助项目(2013J01198)； 华侨大学中青年教师科研提升计划项目(ZQN-YX304)

TM 351

A

1000-5013(2016)05-0536-05