单自由度冲压机构优化设计及其运动仿真

安淑女， 王洪欣

(1. 江苏建筑职业技术学院 机电工程学院， 江苏 徐州 221116;2. 中国矿业大学 机电工程学院， 江苏 徐州 221116)



单自由度冲压机构优化设计及其运动仿真

安淑女1， 王洪欣2

(1. 江苏建筑职业技术学院 机电工程学院， 江苏 徐州 221116;2. 中国矿业大学 机电工程学院， 江苏 徐州 221116)

在冲压机构上定义坐标系，对冲压机构的运动学进行分析，推导出冲压机构滑块的位移、速度及加速度公式.导槽轮廓设计选择n阶贝塞尔曲线，采取优化方法得出冲压机构连杆及驱动杆的最佳尺寸.结合具体实例，在三维建模软件SolidWorks中构建冲压机构实体模型.采用ADAMS软件对其进行运动仿真，得到滑块的运动特性曲线.同时，与传统冲压机构的仿真结果进行对比分析.仿真结果显示：单自由度冲压机构滑块速度和加速度(每个周期滑块大约位于0.3～0.7 s的位置处)比传统冲压机构平稳，能够很好地满足深冲压模具的要求.

冲压机构； 单自由度； 三维建模； 运动仿真

机械冲压机构的滑块运动通常很难调整.但是，在很多金属零部件的深冲压加工过程中，需要对滑块的速度及加速度进行控制，以适应不同产品加工的要求.目前，对冲压机构的研究方法有多种.于大坚等[1]研究了非圆齿轮传动的精密压力机驱动机构，通过改变非圆齿轮形状改变冲压机构滑块的速度.文献[2-3]研究了八连杆冲压机构，对冲压机构的速度和功率进行优化，优化结果采用ADAMS进行动力学仿真.文献[4-6]研究了混合驱动冲压机构运动学的位移、速度及加速度，优化机构尺寸参数，对机构模型进行动力学仿真.文献[7-10]研究了六连杆冲压机构，构造六连杆冲压机构的简图，分析机构滑块运动过程中的位移、速度及加速度，对六连杆冲压机构进行仿真.以往研究的冲压机构大部分应用于浅冲压模具或精度不高的深冲压模具中，对于精度要求较高的深冲压机构却少有人研究.因此，本文研究了用于深冲压模具的机构，并对其动力学进行仿真.

图1　冲压机构简图Fig.1　Stamping mechanism sketch

1　单自由度冲压机构运动分析

单自由度冲压机构简图，如图1所示.该机构是电动机旋转带动驱动杆旋转，驱动杆通过三接头块与连接杆相连，连接杆通过运动带动滑块上下运动，从而实现冲压过程.驱动杆由伺服电动机和控制器驱动，电动机旋转轴上安装混合式光电码器，可以完成驱动杆位置检测.

驱动杆位置以脉冲量计算，根据计算机控制设定值(驱动杆旋转的角度)进行计算，采取D/A转换和放大器将信号输入到伺服电动机控制系统，完成电动机的变速控制.对驱动杆速度曲线和滚筒导槽轮廓的合理设计可以得到新的输出运动特性或提升现有的特性.

图2　冲压机构坐标系Fig.2　Stamping agency coordinates

2　运动学分析

为了引出运动学方程，在单自由度冲压机构上定义坐标系统，如图2所示.

2.1位置、速度及加速度分析

回路方程式可以写为

(1)

用一个长度ri表示驱动杆和连杆的位置向量，用φi表示对应的旋转角度，如图2所示.驱动杆的长度可以表示为

(2)

式(2)中：r2,o是驱动杆的原始长度;Δr2是驱动杆的瞬时长度调整值;Δrini是驱动杆的原始长度调整值.该矢量方程可分割为X，Y方向的标量方程，表示为

(3)

对式(3)两侧进行平方，整理可得

(4)

求解式(4)可得

(5)

因为φ5=φ4-β，所以

(6)

滑块的直线位移为

(7)

同理，对式(3)进行时间的微分，可推得滑块的速度为

(8)

对式(3)进行时间的二次微分，可推得滑块的加速度为

(9)

2.2驱动杆的速度曲线

假设组成机械拉伸冲压机的驱动杆是一个曲柄.驱动曲柄的角位置由一条带有参数t的n阶贝塞尔曲线定义，即

(10)

φ2(t)是一条代表驱动杆角位置由控制点θi定义的贝塞尔曲线.参数t是从0到1的变化时间.贝塞尔曲线的n阶可微分性保证了整个运动的平滑性.因此，驱动杆的角速度ω2(t)和角加速度α2(t)可以由连续的微分方程(10)对时间求导得到，即

(11)

(12)

3　导槽的轮廓设计

驱动杆的瞬时长度调整值Δr2(t)和它对时间的第一阶和第二阶导数也同样可以由一条对应于驱动杆角位置的n阶贝塞尔曲线求得，即

(13)

式(13)中：Δr2(t)是一条代表驱动杆瞬时长度调整值、由控制点λi定义的贝塞尔曲线.

因此，导引槽轮廓上的第i个点的坐标可以表示为

(14)

式(14)中：r2,o是驱动杆的原始长度;φ2,i和Δr2,i分别是对应于导引槽轮廓上第i个点的驱动杆的角位置和瞬时长度调整值.

4　优化设计

基于运动学[11-12]分析可知，速度曲线由变量θ0，…，θn决定，可调节驱动杆的总长由变量λ0，…，λn和rini决定.文中方法采用了一种优化步骤以决定所有的设计变量，优化方程定义如下.最小化等式为

(15)

服从于等式约束条件和不等式约束条件为

(16)

(17)

式(16)～(17)中：Oi是目标函数;ni是目标函数的编号;nc和ng是等式约束条件和不等式约束条件的编号.要注意的是，等式约束条件和不等式约束条件都是在这样的情况下定义的，即所需的输出运动特性是可以实现的.

5　设计实例

使用一条具有11个控制点的10阶贝塞尔曲线代表驱动杆的速度曲线和长度调节量.可以清楚地知道，θ0，λ0，θn和λn是连续循环中的边界条件.因此，θ0= θudc，θn=θudc+2π，λ0=0，λn=0以保证导槽具有一个闭合的轮廓.这里，θudc是当滑块在上死点时对应的曲柄角度位置.在所有的示例中，输入曲柄的平均速度固定为60r·min-1.

在本例设计中，机械冲压机构的有些尺寸是已知的，如表1所示.假设在t=0.3s和t=0.7s之间的前进冲程中，需要恒定速度冲压加工.设计一条速度曲线和确定驱动杆的长度,以满足所需的运动学设计要求和使滑块的加速度峰值最小化.

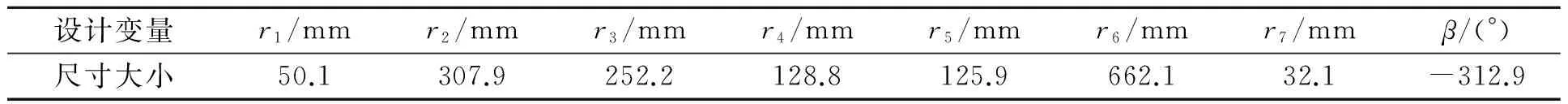
表1　压力机设计尺寸

优化问题被定义为最小化，即

(18)

服从于

(19)

式(18)，(19)中：aRam是滑块的线性加速度；s是滑块的线性位置；smax是滑块最大线性位置；ta是时间;lmax和lmin是驱动杆的最大和最小连杆长度，该驱动杆满足格拉霍夫定律，即“驱动杆当作曲柄”；v是滑块的线性速度；tds和tde是一个特殊区域的开始和结束时间；εv是一个小数.

本例中,驱动杆的速度曲线和瞬时长度调整值的优化控制点，如表2～3所示.

表2　驱动杆速度曲线控制角度

表3　驱动杆长度控制点

(a) 文中模型　　　(b) 文献[8]模型图3　三维实体模型Fig.3　Three dimensional solid model

通过设计变量和优化尺寸创建冲压机构三维实体模型，以及文献[8]的三维实体模型，如图3所示.

将三维实体模型导入到ADAMS软件中进行运动仿真.同时，将文中输入的仿真结果与文献[8]进行了对比，如图4所示.图4中：s为滑块位移；v为滑块速度；a为滑块加速度.运动仿真结果显示，文中优化设计后的冲头速度、加速度(每个周期滑块大约位于0.3～0.7 s的位置处)比文献[8]相对平稳，此优点对于高精密深冲压模具特别有益.同时，在电动机转速固定的某个值时，通过调节驱动杆尺寸，形成滑块不同的速度和加速度，从而满足不同冲压模具件的要求.

6　结束语

对单自由度冲压机构进行优化设计，得出驱动连杆运动的最佳尺寸，借助SolidWorks三维软件构造冲压机构实体模型.采用ADAMS软件对冲压机构进行动力学仿真.仿真结果显示，单自由度冲压机构在深冲压运动过程中(每个运动周期内，滑块大约运动到0.3～0.7 s的位置处)，速度和加速度上下波动较小，振动较小，运动相对平稳，能够很好地满足深冲压模具的要求.因此，该冲压机构冲压的零部件精度较高，在精密冲压件中具有一定的应用价值，为冲压机构的深入研究提供了参考.

[1]于大坚,邬义杰,王彬,等.基于非圆齿轮传动的精密压力机驱动机构设计[J].组合机床与自动化加工技术,2010(12):13-17.

[2]白育全,文学洙.基于ADAMS的八连杆冲压机构的优化设计[J].延边大学学报(自然科学版),2015,41(2):175-178.

[3]SOONG R C,CHANG S B.Simulation and optimization of eight-bar lingkage press mechanism using variable length driving links[J].Mechanism and Machine Theory,2011,46(7):1696-1706.

[4]陈文,傅蔡安.混合驱动冲压机构的运动学分析及参数优化[J].机床与液压,2011,39(7):111-113.

[5]傅蔡安,陈文.混合输入冲压机构的运动学分析及参数优化[J].中国机械工程,2011,22(6):666-670.

[6]刘波.混合驱动九连杆冲压机构的研究[D].太原:中北大学,2013:32-45.

[7]宋梅利,范元勋,祖莉.基于ADAMS的六连杆冲压机构的仿真优化设计[J].南京理工大学学报,2006,30(3):285-287.

[8]SOONG R C.An adjustable six-bar mechanism with variable input speed for mechanical forming presses[J].Transactions of the Canadian Society for Mechanical Engineering,2010,32(4):458-466.

[9]王淑坤.平面六杆压力机构的优化设计[J].机械研究与应用,2003,16(4):20-21.

[10]谢慧萍,季英瑜.基于ADAMS软件的六连杆冲压机构的优化设计[J].轻工机械,2009,27(2):47-50.

[11]席晓燕.金属成形加工机械执行机构的仿真与动力学分析[J].包装工程,2015,36(7):48-54.

[12]刘波,梅瑛,李瑞琴.平面双曲柄冲压机刚柔耦合模型的动态仿真[J].机械传动,2012,36(12):68-71.

(责任编辑： 黄晓楠英文审校： 崔长彩)

Optimization Design and Motion Simulation for Single Degree of Freedom Stamping Mechanism

AN Shu′nyu1， WANG Hongxin2

(1. College of Mechanical and Electrical Engineering，Jiangsu Vocational Institute of Architectural Technology, Xuzhou 221116， China;2. College of Mechanical and Electrical Engineering， China University of Mining and Technology, Xuzhou 221116， China)

The coordinate system is defined on the stamping mechanism, whose kinematics is analyzed to obtain the formulas of displacement, speed and acceleration speed. Then-order Bessel curve is selected for contour design of its guide groove, and an optimization method is used to obtain the best size of the stamping connecting rod and drive rod. In combination with concrete examples, the modeling of stamping mechanism is established using three-dimensional modeling software of SolidWorks. ADAMS software is used to conduct the motion simulation to obtain movement characteristic curve of sliding blocks. Compared to the traditional simulation, the obtained simulation results show that the speed and acceleration speed of stamping mechanism unidirectional sliding blocks (the sliding block in each cycle lies about the location of 0.3-0.7 s) are steadier than traditional stamping mechanism, which can fulfill the requirements for deep stamping mould.

stamping pressure mechanism; single degree of freedom; three-dimensional modeling; motion simulation

10.11830/ISSN.1000-5013.201605005

2015-11-13

安淑女(1965-)，女，副教授，主要从事机械设计与制造的研究.E-mail:anshunv1965@sina.com.

江苏省科研计划项目(11-01502); 中国矿业大学科技基金资助项目(2012B008)

TH 122

A

1000-5013(2016)05-0547-05