多维齿槽转矩优化方法在永磁电机中的应用研究
董淑惠,王 慧,王艾萌
(华北电力大学 电气与电子工程学院,河北 保定 071003)
多维齿槽转矩优化方法在永磁电机中的应用研究
董淑惠,王 慧,王艾萌
(华北电力大学 电气与电子工程学院,河北 保定 071003)
分别采用改变定子齿的形状、调整极弧系数以及磁极偏移的方法来削弱永磁电机的齿槽转矩,并将这3种方法相结合使齿槽转矩进一步优化。通过建立永磁电机的有限元模型,对提出的齿槽转矩抑制方法进行理论分析与有限元验证,并对采用磁极偏移法减小齿槽转矩进行了实验验证。结果表明:改变定子齿的形状、最优极弧系数法和磁极偏移法均有效减小齿槽转矩;而采用三者相结合的方法后,永磁电机的齿槽转矩更是得到极大减小;磁极偏移法的有限元仿真结果和实验果基本吻合,验证了该方法对减小齿槽转矩的有效性。
永磁电机;齿槽转矩;齿的形状;极弧系数;磁极偏移;有限元
0 引 言
随着高性能永磁材料的发展、电力电子器件和控制技术的不断进步,永磁电机引起了人们的广泛关注。因为具有结构紧凑、效率高、转矩密度高等特点,永磁电机在汽车和航空航天等领域得到了广泛应用[1-3]。
然而永磁电机的特有问题之一就是齿槽转矩的存在[4],电枢绕组中电流激励为零时,永磁体和定子铁心的齿槽相互作用在圆周方向上产生的转矩称为齿槽转矩。齿槽转矩的存在会影响永磁电机运行性能:如转矩波动、振动和噪声,因此,研究如何减小齿槽转矩是永磁电机领域非常重要的一个问题。有关齿槽转矩的削弱方法,国内外多名学者专家从电机本体结构出发对其进行过研究,主要是通过改变电机本身结构和参数等方法减小齿槽转矩。
减小永磁电机齿槽转矩的方法有:槽极配合法、磁极偏移、斜槽、斜极、辅助槽、优化极弧系数法、永磁体分体、优化永磁体形状等[4-11]。尽管有各种不同的方法可以削弱齿槽转矩,但是其中的一些方法有明显的缺点,实际中很难广泛应用。例如:定子斜槽或转子斜极的方法,二者削弱齿槽转矩的原理类似,很难做到大规模生产加工,且采用这两种方法会使电机漏磁增加,降低转矩。另外,如果单独采用一种方法,对齿槽转矩的削弱程度是有限的,因此可以采用几种方法的结合使齿槽转矩得到更大的削弱。
本文选用近年来研究较多的分数槽集中绕组永磁电机[12],建立电机有限元模型。针对采用某一种方法对齿槽转矩削弱的有限性,采用改变齿的形状、最优极弧系数法和磁极偏移相结合的方法来尽量减小齿槽转矩。首先对永磁电机齿的形状进行优化,改变定子齿顶高,使得定子齿顶的形状由均匀分布变为呈左右对称的正弦曲线形状;其次,对极弧系数进行分析并优化,削弱齿槽转矩;然后,采用磁极偏移方法,通过削弱特定的谐波次数来达到齿槽转矩优化的目的。
1 多维齿槽转矩优化方法
1.1 采用改变齿的形状方法减小齿槽转矩

图1 电机A的齿形状不同时的磁场分布Fig.1 The distribution of magnetic field for motor A with different shaped teeth
由于齿槽转矩是由永磁体和定子齿槽相互作用引起的,因此定子齿的形状对齿槽转矩有很大的影响。在设计电机之初,就应该考虑避免因为不合适的齿形状引起较大的齿槽转矩。改变定子齿的形状也可以减小齿槽转矩谐波,这和改变磁极形状减小齿槽转矩方法的原理是类似的[13-15],即通过改善气隙磁密的分布(尽量减少漏磁和防止铁心饱和)达到削弱齿槽转矩的目的。为了验证此方法的有效性,建立了6极9槽极弧系数为1的外转子永磁电机模型A,如图1所示。改变定子齿顶高Tp的大小即可改变定子的形状,其余参数保持不变,Tp的变化范围从2.5 mm到0,齿的形状由均匀分布变为呈左右对称的正弦曲线形状。

图2 气隙磁场分布Fig.2 Air-gap field distribution with different shaped teeth

图3 齿的形状对齿槽转矩的影响Fig.3 Influence of tooth shaping on cogging torque
6极9槽电机槽数和极数的最小公倍数NL是18,因此,齿槽转矩波形的周期是20°。图2表示的是Tp的尺寸从2.5 mm到0 mm变化时气隙磁密分布,Tp=0时,气隙磁密曲线较为光滑、正弦。Tp变化时,即改变定子齿的形状对齿槽转矩的影响如图3所示。由此可知,齿的形状改变后,齿槽转矩的幅值由原来的1.30 Nm降为0.84 Nm,齿槽转矩的2次与3次谐波降低较为明显,特别是当Tp为0时,其齿槽转矩降低到最小。
1.2 改变齿的形状和优化极弧系数方法相结合减小齿槽转矩
齿槽转矩是由永磁体和定子齿槽相互作用产生的,齿和槽的磁阻不同且周期性变化,因此齿槽转矩也呈周期性变化。采用能量法对齿槽转矩进行分析,永磁电机的齿槽转矩Tcog表达式可以表示为[16]
(1)
式中:Lef是电机的有效轴长;Bσ是永磁体产生的气隙磁密幅值;Ns是电机槽数;Np是电机极数;μ0是气隙磁导率;Nc是Ns和Np的最小公倍数;R1是气隙内半径;R2是气隙外半径;b0是定子槽口宽;αp是极弧系数;αs是斜槽角度;Kskn定义为斜槽系数。
影响齿槽转矩大小的一个重要参数是极弧系数αp,研究表明,选择恰当的极弧系数可以非常有效地削弱齿槽转矩。极弧系数指的极弧长度占极距的比例。而磁极的极弧系数大小反映了其能够提供磁通量的多少,进而会对齿槽转矩造成影响。另外选择合适的极弧系数,会使电机主极磁场波形更加正弦,改善反电动势波形,进行电机设计时应综合考虑进行选择。
从式(1)可以得出,如果极弧系数满足下列条件时,齿槽转矩将达到最小值。
(2)
从上式(2)可以解出对应最小齿槽转矩的αp的最优解为
(3)
式(3)中,如果k取Nc/Np,那么αp=0,然而这是不可能实现的,因为αp=0,转子上将没有永磁体励磁。当k=0时,αp=1,但是通常在实际应用中也不会用这种方法减小齿槽转矩,因为会有磁极间漏磁现象和磁通边界效应,因此对应最小齿槽转矩的最优极弧系数αp为
(4)
由上式(4)可知,对不同槽极组合和不同转子结构的永磁电机,选择合适的极弧系数都可以减小齿槽转矩。Nc/Np的值越大,最优极弧系数αp的取值也就越多。实际上,由于磁通边界效应的影响,最优极弧系数αp的值会比由式(4)计算结果稍微大一点,修正后的最优极弧系数αp*为
(5)
式中:k1是根据气隙长度的不同而变化的值。显然,为了增大气隙磁通密度,进而提高转矩密度,最优极弧系数的值越大越好,因此,通常选择k=1时对应的极弧系数值。对于6极9槽的电机A由式(4)得出αp=0.667,此时没有考虑k1的值。

图4 极弧系数对齿槽转矩的影响Fig.4 Influence of magnet pole-arc to pole-pitch ratio on cogging torque
图4(a)和(b)分别表示Tp=2.5 mm和Tp=0 mm时,6极9槽电机模型A在不同极弧系数下齿槽转矩波形。比较两个图可得,改变齿的形状将齿槽转矩减小后,再选择一个合适的极弧系数,齿槽转矩会进一步被削弱,齿的形状改变前后最小齿槽转矩的幅值分别为0.4 Nm和0.1 Nm,对应的极弧系数分别为0.7和0.75,由此可知,考虑磁通边界效应后,对应最小齿槽转矩的最优极弧系数αp*比0.667大。
图5(a)和(b)分别表示Tp=2.5 mm和Tp=0时,极弧系数变化时,6极9槽电机模型A的齿槽转矩谐波分析。从图5(b)可以看出,齿的形状改变后齿槽转矩的3次谐波分量几乎在所有的极弧极系数下都为零。当极弧系数为0.8时,齿槽转矩的3次谐波最小值为0.000 8 Nm。
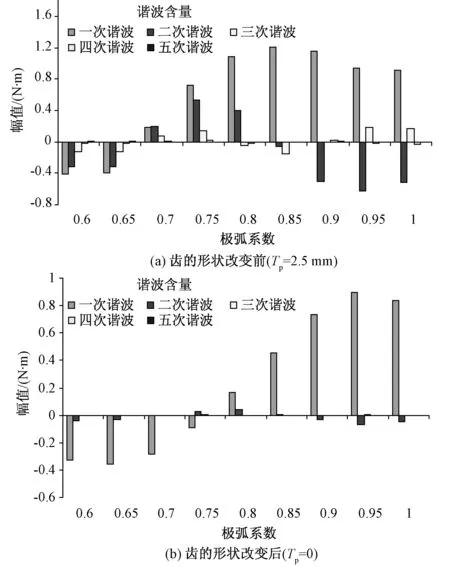
图5 齿槽转矩谐波对比图Fig.5 Comparison chart of cogging torque harmonic
1.3 改变齿的形状和磁极偏移方法相结合减小齿槽转矩
1.3.1 齿槽转矩傅里叶分解
由齿槽转矩的定义,齿槽转矩的表达式也可以写为[17]
(6)
式中:λg是气隙磁通;R是气隙磁阻;θ是转子位置角。
因为齿槽转矩是有周期的,其可以表示为傅里叶级数的形式:
(7)
式中:i是整数,Ti是傅里叶系数。
可以看出电机旋转一周,齿槽转矩的周期是Nc,Nc和定子槽数和转子极数有关。
从式(6)可以看出,在气隙磁通λg或者气隙磁阻的变化率dR/dθ为零的情况下,齿槽转矩可以完全消除。但是气隙磁通λg=0是不可能实现的,因为需要由气隙磁通产生的转矩驱动电机转动。因此理论上来说,保持气隙磁阻R相对于转子位置角θ固定不变,齿槽转矩可以完全消除,然而实际应用中,很难做到齿槽转矩百分百消除,但是可以通过采用一定的方法极大程度地削弱齿槽转矩。
从式(7)可以看出,齿槽转矩公式可用傅里叶级数的形式表示,因此齿槽转矩可以看成是由一系列谐波叠加合成得到的。
永磁电机中一般为多极结构,每个磁极与定子齿槽相互作用都会产生齿槽转矩。一般认为单个磁极产生的齿槽转矩是由各次谐波叠加合成得到的,而整个永磁电机总的齿槽转矩波形是由所有的磁极产生齿槽转矩波形叠加得到的。
以一台简单的2极电机为例说明磁极偏移后的齿槽转矩,一台磁极分布不均匀的2极电机的齿槽转矩表达式如下所示:
(8)
式中:δsh是磁极偏移角度;Tmi是单个磁极产生齿槽转矩的傅里叶系数值。因为总的齿槽转矩波形是由所有磁极齿槽转矩波形叠加合成得到,而每个磁极产生的波形均相同,当其中一个磁极改变了其在转子的初始位置后,齿槽转矩波形可相互抵消。一般条件下,当磁极的齿槽转矩波形偏移半个周期,合成的齿槽转矩会达到最小。
分析此6极电机模型磁极偏移的2种方法:(1)偶次谐波剩余;(2)奇次谐波剩余,下面分别进行分析。
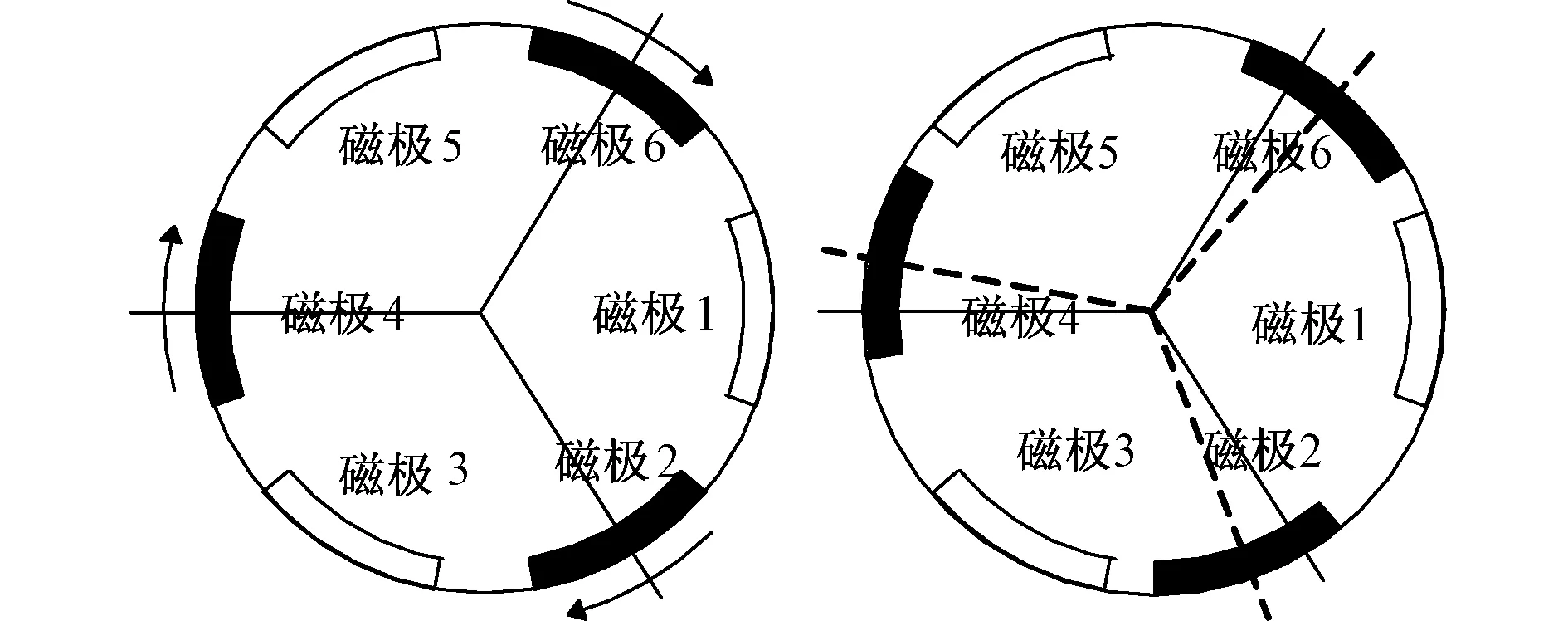
图6 电机A的磁极偏移方法(偶次谐波剩余)Fig.6 The way of displacing magnet on rotor of prototype motor A(even harmonic residual)
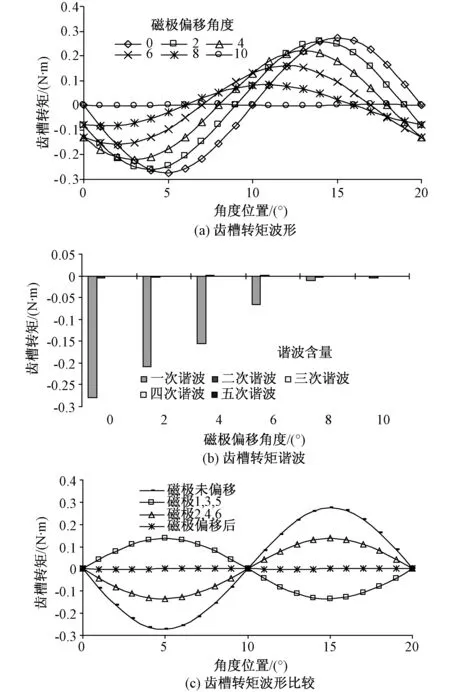
图7 偶次谐波剩余情况的齿槽转矩Fig.7 Cogging torque for the even harmonic residual case
1.3.2 偶次谐波剩余
6极9槽电机模型A按照图6所示的方法进行偏移,最佳偏移角是10°。电机A可认为包含2组磁极,如图6所示的磁极1-3-5与2-4-6,磁极2-4-6相对于磁极1-3-5发生偏移,齿槽转矩分别如下式所示:
(9)
(10)
合成齿槽转矩如下式:
(11)
需要注意的是:这种方法减小了齿槽转矩中的奇数次谐波,而偶数次谐波剩余下来。而且要在极弧系数允许条件下,移动转子上磁极的位置。因为磁极偏移要有足够的空间裕量,所以极弧系数设置为0.7。图7是齿形状改变后,即Tp=0时,按图6所示的方法进行磁极偏移,偏移角不同时得到的齿槽转矩结果,可以看出偏移角是10°时齿槽转矩特别小,幅值为0.006 Nm。值得注意的是,由图7 (a) 和 (c)可以看出,与齿形状未改变相比,改变齿的形状后,得到的齿槽转矩波形变得更光滑,幅值变小。
1.3.3 奇次谐波剩余
6极9槽的电机还可以看成包含3组磁极,如图8所示的磁极1-4,2-5与3-6,磁极2-5与3-6相对于磁极1-4发生偏移,齿槽转矩分别为
(12)
(13)
(14)
合成齿槽转矩为
(15)
式中:Tcog14、Tcog25和Tcog36分别是磁极1-4、2-5和3-6产生的齿槽转矩。
最佳偏移角可由式(16)得为6.66°,一般情况下,由三组磁极合成的齿槽转矩中的某些奇数次谐波会存在,特别是三次谐波。
(16)
图9表示的是极弧系数为0.79的电机模型A使用磁极偏移方法结合改变齿形状的方法的得到的齿槽转矩,图9(b)是齿槽转矩谐波频谱图,从图中我们可以看到,几乎没有齿槽转矩谐波分量。
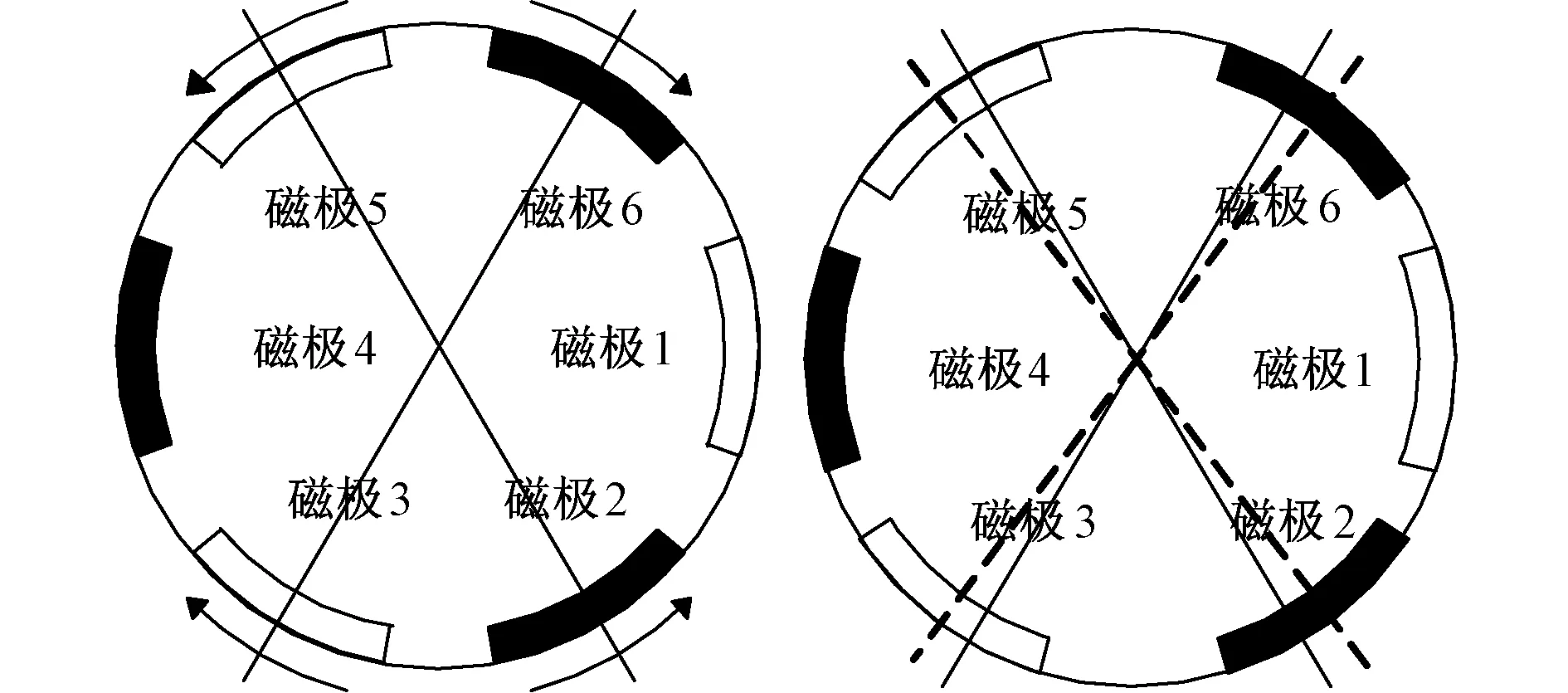
图8 电机A的磁极偏移方法(奇次谐波剩余)Fig.8 The way of displacing magnet on rotor of prototype motor A(odd harmonic residual)

图9 奇次谐波剩余情况下的齿槽转矩Fig.9 Cogging torque for odd harmonic residual case
1.4 方法综合
图10表示的是采用多维齿槽转矩优化技术的结果。
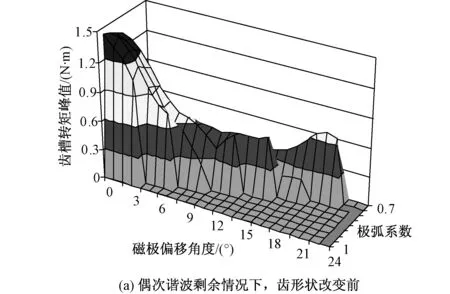

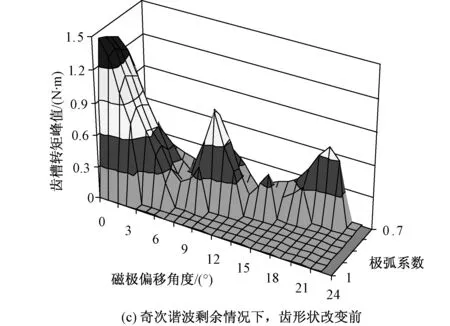

图10 多维齿槽转矩优化技术的结果Fig.10 The final results of the multi-dimensional cogging torque optimization technique
采用改变齿的形状、最优极弧系数和磁极偏移相结合时齿槽转矩峰值的变化,比较和齿的形状改变前后齿槽转矩峰值随磁极偏移角度和极弧系数的变化。可以看出,改变齿的形状,齿槽转矩的峰值明显下降,然后通过选择极弧系数和磁极偏移角度,齿槽转矩能够减小到原来的98%,此综合方法对减小永磁电机的齿槽转矩效果明显。
2 样机试验
为了验证理论分析的正确性,对现有样机采用偶次谐波剩余情况的磁极偏移方法来减小齿槽转矩的有效性进行了试验验证。图11(a)、(b)和(c)是样机部分,此样机的极弧系数是0.65,磁极偏移角度是10°。图11(d)和(e)分别比较了试验实测和有限元仿真得到的齿槽转矩波形和谐波含量,测量结果和仿真结果基本吻合,验证了理论的正确性。




图11 αp=0.65时,齿槽转矩的比较Fig.11 Comparison of cogging torque with αp=0.65
3 结 论
本文分别研究了齿的形状、极弧系数和磁极偏移对永磁电机齿槽转矩的影响。结合有限元软件,分别采用改变齿的形状、优化极弧系数、调整磁极偏移角来减小永磁电机的齿槽转矩,针对这三种方法对齿槽转矩削弱效果不明显的问题,本文提出将三者结合的方法,从而使齿槽转矩得到极大优化,仿真结果验证了该方法对削弱齿槽转矩的有效性。磁极偏移方法的样机试验结果和有限元仿真结果相吻合,对理论分析进行了有效验证。
[1] ZHU Z Q, HOWE D. Electrical machines and drives for electric,hybrid, fuel cell vehicles[J]. IEEE Journals & Magazines,2007, 95( 4): 746-765.
[2] PELLEGRINO G, VAGATI A, GUGLIELMI P,et al.Performance comparison between surface-mounted and interior PM motor drives for electric vehicle application[J]. IEEE Transactions on Industrial Electronics,2012, 59(2): 803-811.
[3] CAO W P, MECROW B C, ATKINSON G J,et al.Overview of electric motor technologies used for more electric aircraft (MEA)[J]. IEEE Transactions on Industrial Electronics, 2012,59( 9): 3523-3531.
[4] 王秀和.永磁电机[M].北京:中国电力出版社,2007.
[5] EL-REFAIE A M,JAHNS T M,NOVOTNY D W.Analysis of Surface Permanent Magnet Machines with Fractional Slot Concentrated Windings[J]. IEEE Transactions on Energy Conversion,2006,21(1):34-43.
[6] LI L, SLEMON G.Reduction of cogging torque in PM motors[J]. IEEE Transactions on Industrial Electronics,1988,24( 6):2901-2903.
[7] LIANG Fang,SOON-O Kwon, TAO Sun,et al.Optimal shape design of double-barriers in single-layer interior PM synchronous motor for reducing torque pulsation[C].Electrical Machines and Systems (ICEMS), Incheon,Korea,2010:1239-1241.
[8] DEODHAR R P, STATION DAVID A, JAHNS T M, et al. Prediction of Cogging Torque using the Flux2MMF D iagram Technique[J]. IEEE Transactions on Industry Applications, 1996, 32(3) : 569-576.
[9] BINNS K, CHAABAN F, HAMEED A.Major design parameters of a solid canned permanent magnet motor with skew magnet[J]. Electric Power Applications, IEEE Proceedings B, 1993,140(3):161-165.
[10] 刘婷,欧阳红林,黄守道,等.基于重复单元削弱永磁风力发电机齿槽转矩[J]. 电工技术学报, 2011,26(12): 43-48.
[11] 黄守道,刘婷,欧阳红林,等. 基于槽口偏移的永磁电机齿槽转矩削弱方法[J]. 电工技术学报,2013,28( 3) : 99-106.
[12] AYMAN M EL-Refaie.Fractional-slot concentrated-windings synchronous permanent magnet machines: Opportunities and challenges[J]. IEEE Transactions on Industrial Electronics,2010,57(1):107-121.
[13] HAN K J, CHO H S, CHO D H,et al.Optimal core shape design for cogging torque reduction of brushless motor using genetic algorithm[J].IEEE Transactions on Magnetics, 2000,36(4):1927-1931.
[14] HUANG D R, YING T F, WANG S J,et al.Cogging torque reduction of a single-phase brushless DC motor[J].IEEE Transactions on Magnetics,1998,34(4): 2075-2077.
[15] YAO Y D, HUANG D R, WANG J C,et al.Simulation study of the reduction of cogging torque in permanent magnet motors[J].IEEE Transactions on Magnetics,1997, 33(5):4095-4097.
[16] ZHU L, JIANG S Z, ZHU Z Q, et al.Analytical methods for minimizing cogging torque in permanent-magnet machines[J].IEEE Transactions on Magnetics,2009,45(4):2023-2031.
[17] SUNG S J, PARK S J, JANG G H. Cogging torque of brushless DC motors due to the interaction between the uneven magnetization of a permanent magnet and teeth curvature[J].IEEE Transactions on Magnetics,2011,47(7):1923-1928.
Application Study on Optimization Method of Multi-dimensional Cogging Torque in Permanent Magnet Machines
DONG Shuhui, WANG Hui, WANG Aimeng
(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)
Cogging torque of permanent magnet machine is reduced by applying the methods of changing the shape of stator tooth, adjusting the pole-arc coefficient and magnet shifting. And these three methods can be combined to further improve the cogging torque. Finite element model of permanent magnet machine is established to make theoretical analysis and finite element verification of the proposed inhibition method of cogging torque. The method of using magnet shifting to reduce cogging torque is verified by experiment. The results indicates that cogging torque are efficiently decreased by changing the shape of stator tooth, optimizing pole-arc coefficient and magnet shifting; what’s more, cogging torque of permanent magnet machine can be dramatically reduced by combing these three methods. Finite element simulation result of magnet shifting is consistent with the experiment result, which verified the validity of this method to reduce the cogging torque.
permanent magnet machine; cogging torque; tooth shape; pole-arc coefficient; magnet shifting; finite element
10.3969/j.ISSN.1007-2691.2017.02.09
2016-05-13.
教育部中央高校基本科研业务费专项资金项目(2014MS95).
TM315
A
1007-2691(2017)02-0060-08
董淑惠(1978-),女,讲师,研究方向为风力发电机控制技术;王慧(1990-),男,硕士研究生,研究方向为永磁同步电机设计及优化;王艾萌(1963-),女,教授,硕士生导师,研究方向为永磁同步电机设计与控制。

