Cr掺杂对ZnO最小光学带隙和吸收光谱的影响*
高艺涵,侯清玉,赵春旺,2
(1.内蒙古工业大学 理学院物理系,呼和浩特 010051; 2.上海海事大学 文理学院,上海 201306)
Cr掺杂对ZnO最小光学带隙和吸收光谱的影响*
高艺涵1,侯清玉1,赵春旺1,2
(1.内蒙古工业大学 理学院物理系,呼和浩特 010051; 2.上海海事大学 文理学院,上海 201306)
当Cr掺杂ZnO的摩尔数为0.0313~0.0625的范围内,掺杂体系的最小光学带隙宽度和吸收光谱分布随Cr掺杂浓度的变化出现了两类相反的实验结果。为了解决本问题,采用密度泛函理论(DFT)框架下的广义梯度近似(GGA+U)平面波超软赝势方法,用PBE泛函的计算方案来描述电子间的交换关联能,对未掺杂ZnO和3种不同浓度Cr掺杂ZnO超胞模型进行了能带结构、态密度、差分电荷密度、布居值以及吸收光谱的计算。结果表明,当Cr掺杂摩尔数为0.0313~0.0625的范围内,随着Cr掺杂量增加,掺杂体系的晶格常数和体积增大,总能量和形成能减小,结构更稳定,掺杂更容易,最小光学带隙宽度增大,吸收光谱显著蓝移。计算结果与实验结果相一致,并合理解释了存在的问题。这对制备Cr掺杂ZnO中实现短波长光学器件有一定的理论指导作用。
Cr掺杂ZnO;光学带隙;吸收光谱;第一性原理
0 引 言
ZnO室温光泵浦紫外受激辐射现象报道[1]后,这种材料重新引起了人们的重视,并迅速成为了新的短波长半导体材料的研究热点。
ZnO是1种直接宽带隙半导体材料[2],室温下带隙宽度为3.37 eV,在近紫外光区,对可见光透明,激子结合能为60 meV。氧化锌的带隙和激子束缚能较大,透明度高,有优异的常温发光性能。在压电、光电等方面有良好的化学稳定性,因此,受到本研究领域的广泛关注。
有效元素掺杂ZnO中已成为研究半导体材料物性的首选之一[3],例如,Ylmaz等[4]采用喷雾热分解法,研究了Cr掺杂ZnO磁光性能的影响,结果表明,当尺度为5 μm,Cr掺杂量为0.011~0.046的范围内,随着Cr掺杂量增加,带隙变窄,红移更显著。Sayed等[5]通过溶胶-凝胶法,研究了Cr掺杂ZnO结构和光学性质的影响,结果表明,当尺寸为308~330 nm的范围内,Cr掺杂量为0~0.098的范围内,随着Cr掺杂量增加,最小光学带隙变窄,吸收光谱红移更显著。Iqbal等[6]采用电子束蒸镀法,研究了Cr掺杂ZnO结构和光学性质(尺寸为1 μm×1 μm),结果表明,在掺杂量为0~7.7%(原子分数)的范围内,随着Cr掺杂量增加,带隙变窄,掺杂体系吸收光谱红移更显著。Liu等[7]采用溶胶-凝胶法,研究了Cr掺杂ZnO(尺寸为11.1~ 26.2 nm的范围内)的表面形态和光学性质,结果表明,在掺杂量为0~3%(原子分数)的范围内,随着Cr掺杂量增加,掺杂体系光学带隙变宽,吸收光谱蓝移更显著。Ju等[8]利用分光光度计来测量基片为石英的Cr掺杂ZnO吸收光谱分布的影响,结果表明,当尺寸为31.42~52.37 nm的范围内,Cr掺杂量为0~9%(摩尔分数)的范围内,随着Cr掺杂量增加,带隙宽度增加,吸收光谱蓝移更显著。Shah等[9]采用溶胶-凝胶法,研究了Cr掺杂ZnO光学性能的影响,结果表明,当尺寸为54~57 nm的范围内,掺杂体系带隙变宽,吸收光谱蓝移。
在理论计算方面,Weng等[10]采用GGA的平面波超软赝势方法,研究了Cr掺杂和点缺陷对ZnO磁性能的影响,结果表明,Cr掺杂和Zn空位共存容易形成,并且,掺杂体系铁磁性最稳定。Li等[11]采用GGA的平面波超软赝势方法,研究了Cr掺杂ZnO电子结构和光学性质,结果表明,在掺杂量为0~12.5%(摩尔分数)的范围内,随着Cr掺杂量增加,最小光学带隙变宽,吸收光谱发生蓝移。Wang等[12]采用GGA的平面波超软赝势方法,研究了Cr掺杂、锌空位和氧空位共存在ZnO中的磁性影响,结果表明,Cr双掺杂无空位、Cr双掺杂与锌空位共存、Cr双掺杂与氧空位共存的不同条件下,Cr和Cr间距不同,掺杂体系磁矩大小不同。
迄今为止,虽然,在国内外Cr掺杂ZnO光电磁性能影响的研究有一定的进展,但是,Cr掺杂ZnO吸收光谱分布的影响仍存在着分歧。如,在实验文献[4-6]中,当限定的Cr掺杂量范围内,吸收光谱发生红移,同时,Cr掺杂量越大,红移越显著。这与Cr掺杂量相近的文献[7-9]的实验结果相悖,目前尚未有合理的解释。本问题的理论解释是,由于文献[4-6]在实验中使用的掺杂体系尺度远远大于纳米尺度范围,尺度效应为经典效应;而文献[7-9]的实验中使用的掺杂体系为纳米尺度(1~100 nm)范围内,量子尺度效应显著。所以,文献 [4-6,7-9]的Cr掺杂量相近的条件下,掺杂体系吸收光谱发生了分歧。如果Cr掺杂ZnO要想获得吸收光谱红移效应,实验中除了控制Cr掺杂量外,同时必须控制掺杂体系的尺度大于纳米尺度。本文是在1 nm左右尺度的超胞模型中进行了探究,虽然与文献[7-9]的空间尺度相比较小,但是,量子尺度效应相一致,所以,吸收光谱分布的计算结果能够证明文献[7-9]实验结果的变化趋势。如果在超晶格模型中进行研究,能够实现与文献[7-9]的晶体尺度相一致,由于计算条件的限制,只能半定量证明文献[7-9]实验结果的变化趋势。本文显示,如果Cr掺杂ZnO要想获得吸收光谱蓝移效应,实验中除了控制Cr掺杂量外,必须控制掺杂体系在纳米尺度范围内。虽然,前人用传统的广义梯度近似(GGA)或局域密度泛函近似(LDA),广泛研究了Cr掺杂对ZnO电子结构和光学性能的影响,但是,近期软件功能的发展,前人研究工作需要完善和发展。因此,本文采用第一性原理GGA+U的平面波超软赝势方法,研究Cr掺杂对ZnO最小光学带隙和吸收光谱的影响,计算结果与实验结果[7-9]的变化趋势相符合,本文有一定的理论参考价值。
1 模型及计算方法
六方纤锌矿结构的ZnO,空间群P63MC,对称性C6V-4,单胞由两个六方密堆积结构格子沿c轴平移套构而成。分别构建模型为未掺杂ZnO(1×1×1)单胞模型,一个Cr原子替换一个Zn原子的Zn0.9687Cr0.0313O(2×2×4)、Zn0.9583Cr0.0417O(2×2×3)和Zn0.9375Cr0.0625O(2×2×2)超胞模型如图1所示。

图1 理论模型
采用MS6.0软件中的GGA+U平面波超软赝势方法,用PBE泛函描述交换-关联能,几何结构优化时,能量的精度为平均每个原子1.0×10-5eV,作用在每个原子上的最大力为0.3 eV/nm,最大公差偏移为1.0×10-4nm,最大内应力为0.05 GPa。布里渊区K点分别设置为9×9×6(1×1×1未掺杂单胞)、4×4×1(2×2×4超胞)、4×4×2(2×2×3超胞)和4×4×2(2×2×2超胞)。对未掺杂ZnO单胞的截断能收敛性进行了测试,以截断能为单因子变量,测试结果如图2所示。从图2看出,系统总能量在320 eV开始收敛,380 eV左右系统总能量已经有很好的收敛,故所有计算模型的截断能均选取为380 eV。模型中Zn、Cr、O原子的电子组态分别设置为Zn 3d104s2、Cr3d54s1、O 2s22p4。能量计算采用电子自旋极化处理。由于传统的 GGA 平面波超软赝势方法,严重低估了金属氧化物的带隙。传统的GGA方法,在计算中过高地估算Zn3d态能量,使得Zn3d态与O2p态杂化增强,价带宽度偏大,这是由于Zn3d态与O2p态共同杂化形成的,从而引起了ZnO带隙偏低。

图2 未掺杂ZnO截断能收敛性测试
Fig 2 The test of energy convergence as the cut-off varied for undoping ZnO
采用GGA+U的方法修正带隙,如果Zn3d态上+Ud,Zn值的话,O2p态上也应该同时+Up,O值进行修正,这与文献[15-16]中的理论解释相一致。经尝试后发现,未掺杂ZnO中的Zn的3d态和O的2p态分别取Ud,Zn=5.5 eV[13]和Up,O=8.0 eV[13]较理想,对掺杂体系中的Zn的3d态和O的2p态仍然分别取Ud,Zn=5.5 eV[13]和Up,O=8.0 eV[13],Cr的3d态采用软件默认的取Ud,Cr=2.5 eV[14]较理想。
2 结果与讨论
2.1晶格结构和稳定性分析
几何结构优化后,未掺杂ZnO体系的晶格参数a=b=0.3249 nm,c=0.5205 nm,α=β=90°,γ=120°。与实验测量的a=0.3256 nm,c=0.5218 nm[17]非常接近,偏差<1%,这与实验结果[7]相符合,参数设置是合理的。所有体系折合后的晶格结构参数,列于表1中。计算结果与实验结果[7-9]相符合。从表1可以看出,Cr3+掺杂后对体系体积有一定的影响。主要有两点:(1)由于Cr3+半径(0.0615 nm)比Zn2+半径(0.074 nm)小,Cr3+替换Zn2+使晶体体积减小;(2)由于Cr3+替换一个Zn2+时,掺杂体系中产生多余的一个正电荷,多余的正电荷之间相互库仑排斥力增大,掺杂体系体积变大。由于后者的作用比前者的作用强,所以,总的效果是,在掺杂量为0.0313~0.0625的范围内,两种因素共同影响下,随着Cr掺杂量增加,体系体积增加,体系总能量减小,稳定性变强。计算结果与实验结果[8]相吻合。
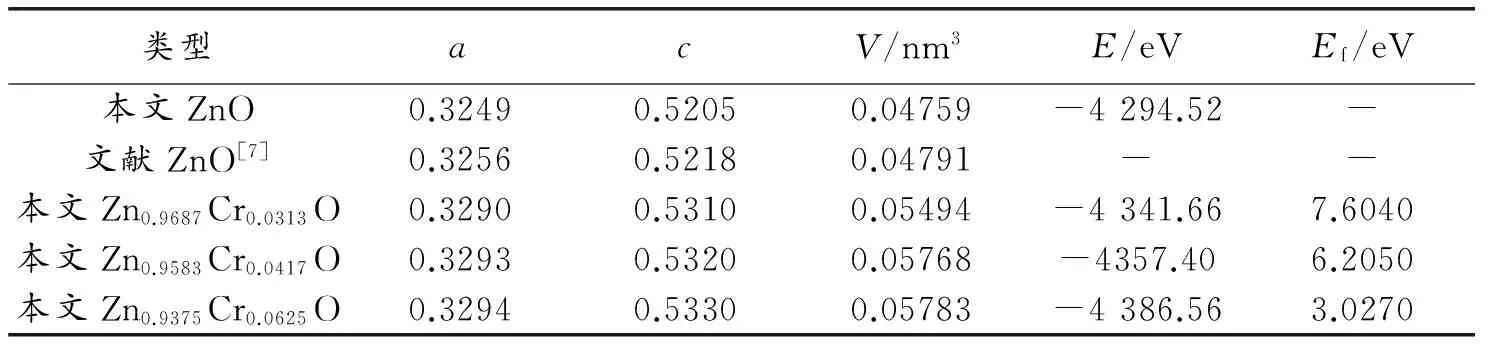
表1 几何结构优化后,Cr掺杂前后ZnO体系的物理参数
为了研究Cr掺杂对掺杂体系稳定性和掺杂难易程度的影响,对所有模型在几何结构优化的基础上,分别计算掺杂体系的形成能,并将结果列于表1中。形成能Ef用以下公式[13]计算
(1)
其中,EZnO∶Cr为掺杂后体系总能量,EZnO为相同大小未掺杂ZnO体系总能量,EZn和ECr分别为基态金属晶体中单个Zn原子和Cr原子的总能量。由计算结果看出,在本文限定的掺杂量范围内(x=0,0.0313,0.0417,0.0625),随着Cr掺杂量增加,掺杂体系形成能降低,结构更稳定。这与总能量分析结果相吻合。结果表明,Cr掺杂量越增加,掺杂越容易。另外,查阅文献[17]后发现,当Cr掺杂量为x=0.1时,掺杂体系仍保持六方纤锌矿结构的要求,结构无相变,所以,本文选取最大Cr掺杂量为x=0.0625时,仍满足六方纤锌矿结构的要求。
2.2布居值分析
计算得未掺杂ZnO和体系Zn0.9375Cr0.0625O的布居值和键长,结果列于表2中。
表2未掺杂ZnO和掺杂后体系Zn0.9375Cr0.0625O的键长和Mulliken布居值
Table 2 Bond length and Mulliken population of undoped ZnO and Zn0.9375Cr0.0625O

键型键长/nm布居值ZnOZn-O(∥c)Zn-O(⊥c)0.19840.19750.210.43Zn0.9375Cr0.0625OCr-O(∥c)Cr-O(⊥c)0.18860.18880.400.46
从表2可看出,与未掺杂ZnO布居值和Zn—O键长相比,掺杂体系无论平行于c轴还是垂直于c轴方向的Cr—O键长均减小,平行于c轴方向或垂直于c轴方向的Cr-O布居值增大。结果表明,掺杂后体系共价键增强,离子键减弱,稳定性增强。计算结果与2.1节的稳定性分析结果相一致。
2.3差分电荷密度分析
为了讨论ZnO掺杂前后原子之间的相互作用,计算得Cr掺杂前后体系的差分电荷密度分布如图3(a)和(b)所示。从图3(a)和(b)看出,与未掺杂ZnO体系相比较,掺杂体系Zn0.9375Cr0.0625O的Cr-O原子之间的电子云明显比未掺杂ZnO体系Zn-O原子之间的电子云重叠变强。结果表明,掺杂后体系共价键增强,离子键减弱,稳定性增强。计算结果与2.1节的稳定性分析以及2.2节的布居值分析结果相吻合。
2.4轨道电荷分析
计算得体系Zn0.9687Cr0.0313O、Zn0.9583Cr0.0417O和Zn0.9375Cr0.0625O的轨道电荷分布如表3所示。从表3可看出,掺杂体系随Cr掺杂量增加,O原子2s轨道,Zn原子3d态电荷数不变,O原子2p态,Cr原子4s态和3d态电荷数均变小,Zn原子4s态电荷数增大。
2.5未掺杂ZnO体系的能带结构及态密度分析
采用GGA+U的方法,对Zn的3d态和O的2p态分别取U=5.5和8.0 eV[13]计算得未掺杂ZnO体系的能带结构及态密度分布如图4(a)和(b)所示。结果表明,未掺杂ZnO半导体为直接宽带隙半导体,体系的最小光学带隙为3.371 eV(从价带顶G点到导带最底点的间距),这与实验结果[8]相符合。由图4(b)看出,未掺杂ZnO体系的价带主要由Zn的3d态和O的2p态杂化构成,而价带顶主要由O的2p态决定;导带底由Zn的4s态决定。

图3 差分电荷密度分布图
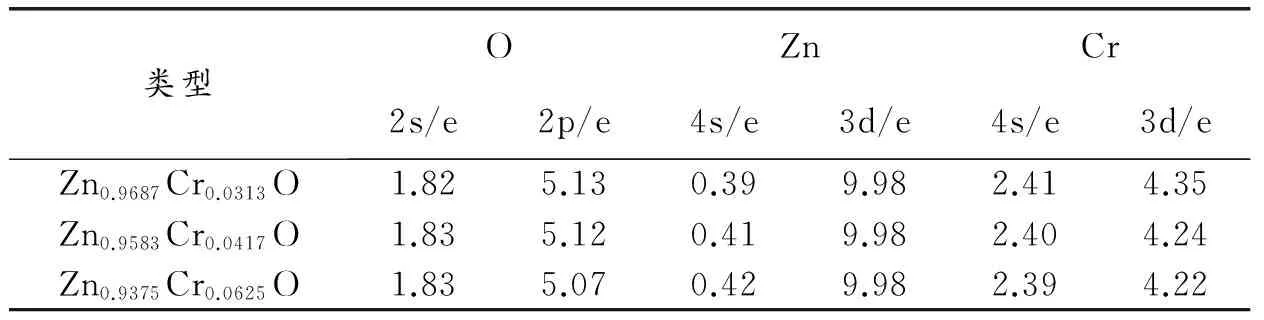
类型OZnCr2s/e2p/e4s/e3d/e4s/e3d/eZn0.9687Cr0.0313O1.825.130.399.982.414.35Zn0.9583Cr0.0417O1.835.120.419.982.404.24Zn0.9375Cr0.0625O1.835.070.429.982.394.22
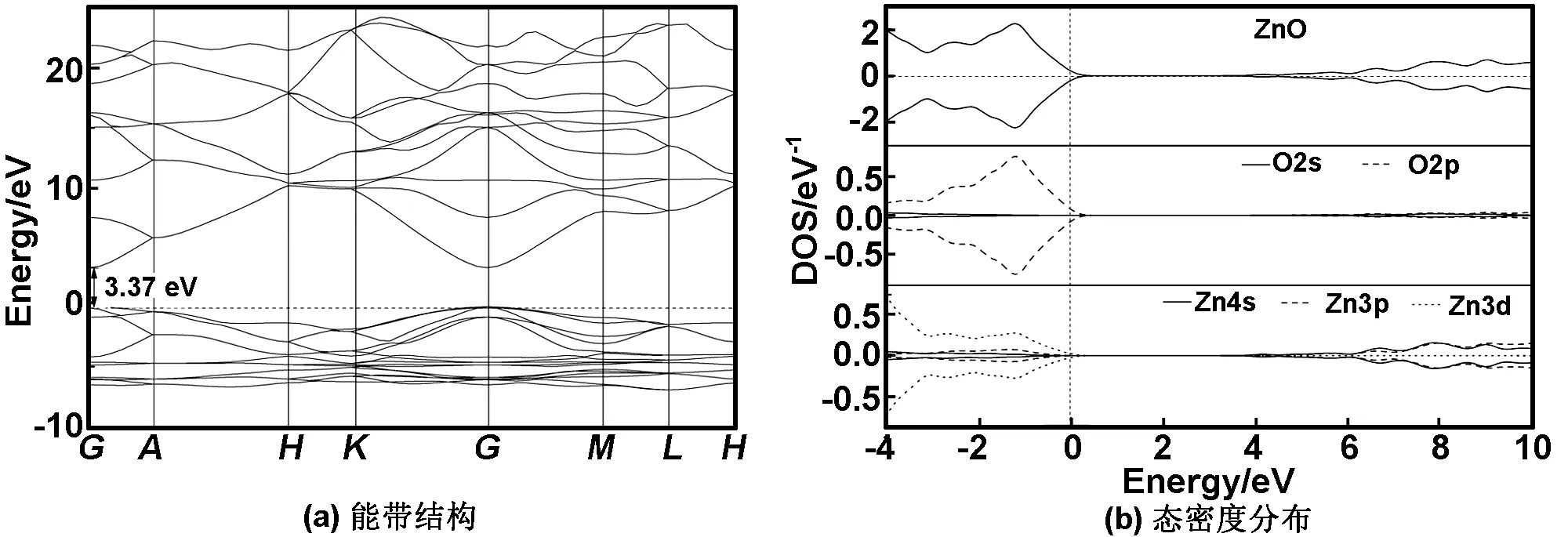
图4 未掺杂ZnO体系的能带结构和态密度分布
2.6Cr掺杂ZnO体系的最小光学带隙分析
计算得Zn0.9687Cr0.0313O、Zn0.9583Cr0.0417O和Zn0.9375Cr0.0625O超胞的能带结构如图5(a)-(c)所示。从图5(a)-(c)可以看出,掺杂体系均表现为n型半导体,掺杂体系最小光学带隙(最小光学带隙是指价带顶G点到费米能级的间距)分别约为3.492,4.088和4.247 eV。为了观察方便,以纵轴为最小光学带隙用Eg表示,以横轴x为Cr掺杂量,二者的关系如图6所示。从图6可看出,随着Cr掺杂量增加,掺杂体系最小光学带隙变宽。计算结果与实验结果[8]相吻合。

图5 能带结构分布图
2.7Cr掺杂ZnO体系的态密度分析
由计算可得Zn0.9687Cr0.0313O、Zn0.9583Cr0.0417O和Zn0.9375Cr0.0625O超胞的分波态密度分布如图7(a)-(c)所示。
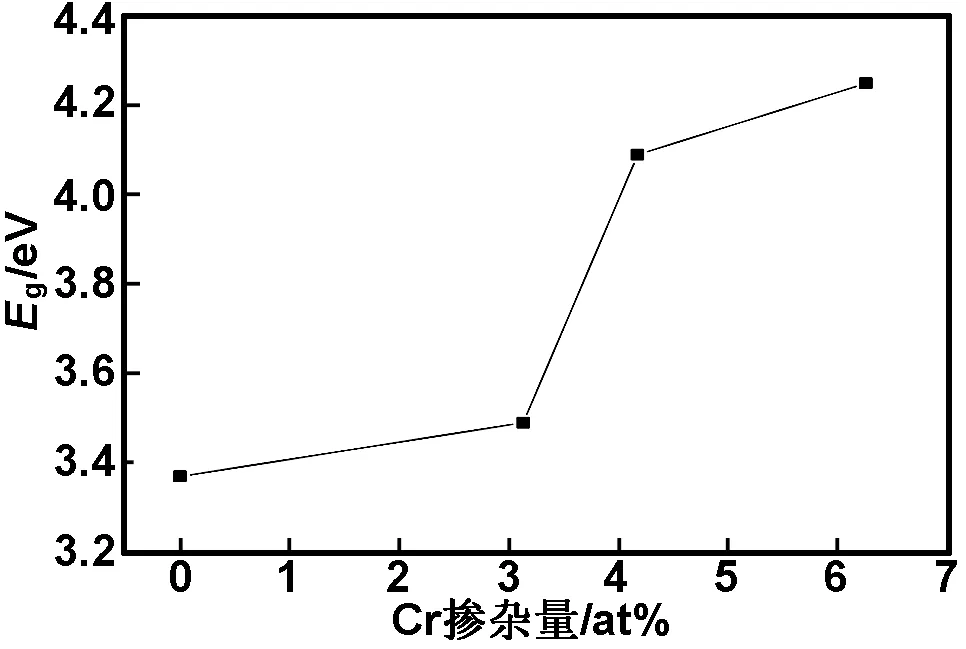
图6不同Cr掺杂量的ZnO体系最小光学带隙宽度分布图
Fig 6 Optical band gap relationship with Cr doping concentration of x
由最小光学带隙宽度的定义知道,由于费米能级0 eV不变,那么,n型半导体的掺杂体系最小光学带隙宽度主要由价带顶位置来决定。在Zn0.9687Cr0.0313O、Zn0.9583Cr0.0417O和Zn0.9375Cr0.0625O超胞的价带中,存在p-p态相互作用和p-d态排斥作用,其中,如果p-p态相互作用增强,使其价带向低能级方向移动;如果p-p态相互作用减弱,使其价带向高能级方向移动。如果p-d态排斥效应增强,使其价带向高能级方向移动;如果p-d态排斥效应减弱,使其价带向低能级方向移动。从图7(a)-(c)看出,随着Cr掺杂量增加,价带中杂化耦合的O2p态、Zn3p态减弱,Zn3d态不变,Cr3d态减弱。这与2.4的轨道电荷分析结果相一致。因此,随着Cr掺杂量增加,p-d态排斥效应减弱程度大于p-p态相互作用减弱程度。所以,总的效果是,随着Cr掺杂量增加,掺杂体系价带下移,最小光学带隙宽度变宽。这与2.6节的能带结构分析结果相一致。

图7 态密度Zn0.9687Cr0.0313O 体系,Zn0.9583Cr0.0417O体系,Zn0.9375Cr0.0625O体系
2.8吸收光谱分析
在线性相应范围内,固体中光的复介电常数
来描述,其中,ε1(ω)为介电常数的实部;ε2(ω)为介电常数的虚部
固体的光吸收系数α(ω)可以由直接跃迁概率的定义和Kramers-Kronig色散关系求得。ε1(ω)、ε2(ω)及α(ω)的表达式如下
(2)
(3)
(4)
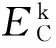
采用GGA+U的方法,计算未掺杂ZnO、Zn0.9687Cr0.0313O、Zn0.9583Cr0.0417O和Zn0.9375Cr0.0625O超胞的吸收光谱分布如图8所示。当掺杂量为0.0313~0.0625的范围内,随着Cr掺杂量的增加,体系的吸收光谱蓝移增强。计算结果与最小光学带隙变化趋势相吻合。这与实验结果[7-9]相一致。
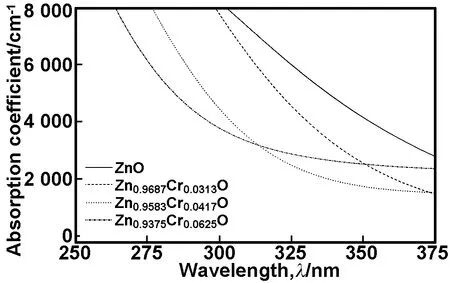
图8未掺杂ZnO,Zn0.9687Cr0.0313O,Zn0.9583Cr0.0417O和Zn0.9375Cr0.0625O体系的吸收光谱分布
Fig 8 The absorption spectra of undoped ZnO,Zn0.9687Cr0.0313O,Zn0.9583Cr0.0417O and Zn0.9375Cr0.0625O
3 结 论
采用密度泛函理论(DFT)框架下的GGA+U平面波超软赝势方法,对所有模型进行几何结构优化和能量计算,得到如下结论:在限定的掺杂量范围内,随着Cr掺杂量增加,体系晶格常数增大,体积增大,总能量减小,体系形成能降低,结构更稳定,掺杂更容易,体系的最小光学带隙变宽,吸收光谱分布蓝移增强。这对设计和制备Cr掺杂在ZnO中获得新型短波长光学器件有一定的参考价值。
[1]Bagnall D M,Chen Y F,Zhu Z,et al.High temperature excitonic stimulated emission from ZnO epitaxial layers [J].Appl Phys Lett,1998,73(8):1038-1040.
[2]Srikant V,Clarke D R.On the optical band gap of zinc oxide [J].J App Phys,1998,83(10):5447-5451.
[3]Tang W,Cameron D C.Aluminum-doped zinv-oxide transparent conductors deposited by the sol-gel process [J].Thin Solid Films,1994,238(1):83-87.
[5]Sayed A M E,Taha S,Said G,et al.Structural and optical properties of spin coated Zn1-xCrxO nanostructures [J].Superlattice Microst,2013,60:108-119.
[6]Iqbal A,Mahmood A,Muhammad K T,et al.Structural and optical properties of Cr doped ZnO crystalline thin films deposited by reactive electron beam evaporation technique [J].Prog Nat Sci-Mater,2013,23(1):64-69.
[7]Liu Y,Yang J H,Guan Q F,et al.Effects of Cr-doping on the optical and magnetic properties in ZnO nanoparticles prepared by sol-gel method [J].J Alloy Compd,2009,486:835-838.
[8]Ju J,Wu X M,Zhuang L J.Study on the structure and optical properties of Zn1-xCrxO films by rf magnetron sputtering technique [J].Int J Mod Phys B,2008,22(30):5279-5287.
[9]Shah A H,Manikandan E,Ahamed M B,et al.Antibacterial and blue shift investigations in sol-gel synthesized CrxZn1-xO nanostructures [J].J Lumin,2014,145:944-950.
[10]Weng Z Z,Huang Z G,Lin W X.Magnetism of Cr-doped ZnO with intrinsic defects [J].J Appl Phys,2012,111:113915.
[11]Li L Y,Wang W H,Liu H,et al.First principles calculations of electronic band structure and optical properties of Cr-doped ZnO [J].J Phys Chem C,2009,113:8460-8464.
[12]Wang F G,Pang Z Y,Lin L,et al.Theoretical study of the magnetic interaction of Cr doped ZnO with and without vacancies [J].J Magn Magn Mater,2009,321:3067-3070.
[13]Guo S Q,Hou Q Y,Zhao C W,et al.Study of the effect of Cu heavy doping on band gap and absorption spectrum of ZnO [J].Chem Phys Lett,2014,614:15-20.
[14]Anisimov V I.Corrected atomic limit in the local density approximation and the electronic structure of d impurities in Rb [J].Phys Rev B,1994,50:23-29.
[15]Sheetz R M,Ponomareva I,Richter E,et al.Defect-induced optical absorption in the visible range in ZnO nanowires [J].Phys Rev B,2009,80:195314
[16]Lathiotakis N N,Andriotis A N,Menon M.Codoping:a possible pathway for inducing ferromagnetism in ZnO [J].Phys Rev B,2008,78:193311
[17]Kumar K,Chitkara M,Sandhu I S,et al.Photocatalytic and magnetic properties of Zn1-xCrxO nanocomposites prepared by a co-precipitation method[J].Mat Sci Semicon Proc,2015,30:142-151.
Effect of Cr-doping on the optical bandgap andabsorption spectra of ZnO
GAO Yihan1,HOU Qingyu1,ZHAO Chunwang2
(1.College of Science,Inner Mongolia University of Technology,Hohhot 010051,China;2.College of Arts and Sciences,Shanghai Maritime University,Shanghai 201306,China)
The studies of absorption spectra of Cr-doped ZnO have presented two contradictory experimental results,which are the red shift and blue shift on the optical bandgap and absorption spectra when the mole fraction of Cr increases in a range from 0.0313 to 0.0625.To solve this contradiction,based on the first-principles plane-wave pseudopotential of the spin-polarized density functional theory(DFT),we set up four models for Zn1-xCrxO(x=0,0.0313,0.0417,0.0625)to calculate the band structure,density of state,difference charge density,population and absorption spectra using the method of generalized gradient approximation(GGA+U).The calculation results indicate that with the increase of mole fraction of Cr in a range from 0.0313 to 0.0625,the lattice parameters and the volume of doping systems increases,the total energy decreases,the formation energy decreases,thereby the doping becomes easier,and the doping system becomes more stable.Meanwhile,the optical bandgap of the doping system becomes wider,which suggests that absorption spectra of Cr-doped ZnO systems would have a blue shift.The calculation results are consistent with the experimental data.And the contradiction of blue shift and red shift of Cr-doped ZnO systems has been explained reasonably.These results may contribute to improve the design and the preparation of short wavelength optical devices from Cr-doped ZnO.
Cr-doped ZnO; optical bandgap; absorption spectra; first-principle
1001-9731(2016)09-09106-06
国家自然科学基金资助项目(61366008,11272142);内蒙古自治区高等学校科学研究资助项目(NJZZ13099)
2015-08-14
2016-03-24 通讯作者:侯清玉,E-mail:by0501119@126.com
高艺涵(1991-),女,内蒙古乌兰浩特人,在读硕士,师承侯清玉教授,从事材料的模拟计算研究。
O47
ADOI:10.3969/j.issn.1001-9731.2016.09.020

