堆叠方法与堆叠层数对扶手型石墨烯纳米带电子能带的影响*
黄 瑞, 童国平
(浙江师范大学凝聚态物理研究所,浙江金华 321004)
0 引言
2004年,在英国的曼彻斯特大学实验室里,Novoselov等[1]利用机械劈裂力学微加工的方法成功地制备出了单层石墨材料(graphene),其中还包括单层在内的少层石墨和其他二维原子晶体.近几年来,由于graphene独特的电子特性,使得全世界的目光汇聚到这一具备高强度和优良导电性能的轻薄材料上,越来越多的研究者纷纷涌入这一热潮之中,并对其做了大量的研究工作,例如能带结构[2]、量子霍尔效应[3]、朗道能级[4]、拉曼谱[5]及输运性质[6]等.时隔 6 年,现任英国曼彻斯特大学教授的安德烈·海姆和康斯坦丁·诺沃肖洛夫,因研究二维石墨烯的开创性实验而荣获2010年的诺贝尔物理学奖.
石墨烯及其衍生物诱人的物理性质和在纳米电子学中潜在的应用价值,为研究低维物理现象提供了一个很好的机遇,将石墨烯进行剪裁可形成一维的碳纳米带(GNRs).从几何结构上讲,GNRs与碳纳米管(CNTs)密切相关,根据GNRs边缘处碳原子具有的不同拓扑形状,也可将其分为扶手椅型石墨烯纳米带(AGNRs)和锯齿型石墨烯纳米带(ZGNRs).对于AGNRs,根据它的带宽分为金属和绝缘体2种类型,文献[7]给出了AGNRs的波函数和能带能隙解析式及最近邻、次紧邻和三紧邻的跳跃能的紧束缚模型.但对于少层的AGNRs来说,层与层之间存在着范德华力.由于堆叠的方式不同,可以沿着层数增加的方向将其分为AA堆叠、AB堆叠、ABC堆叠等.为此,本文采用了紧束缚模型理论[8],详细讨论了AA堆叠与AB堆叠双层AGNRs能带结构的解析解,以及少层堆叠AGNRs能带结构的解析解,并将计算结果进行了对比分析.
1 理论方法和模型
1.1 单层扶手型石墨烯纳米带
单层扶手型石墨烯纳米带的单位晶格中有2个碳原子,根据布洛赫定理,电子在周期性位势下的波函数可表示成平面波与周期性函数的乘积,即

于是,可得到单层扶手型石墨烯纳米带2个子晶格的波函数如下:

由式(1)和式(2)可以求解出本征能量,即
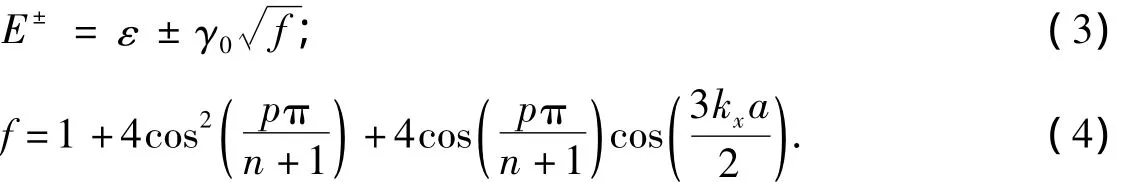
式(3)~式(4)中:kx是在x方向上的波矢;a是C原子之间的键长近邻B原子的跳跃能积分;E+为能量的价带;E-为能量的导带.
1.2 少层扶手型石墨烯纳米带
1.2.1 AA 堆叠法
图1为AA堆叠双层AGNRs,所有1层碳原子直接对应2层碳原子(上下对称).单位晶包共有2N个碳原子,同层内的碳原子间键长为a=0.142 nm,两层石墨的间距为b=0.335 nm.
为解出能量本征值,由薛定谔方程得到的哈密顿矩阵[Hij]是一个4×4矩阵

图1 AA堆叠双层AGNRs

其中:H11,H12,H21,H22均为2 ×2 的方阵.最后得到本征能量为

式(5)中:E±1分别为1层与2层能量的价带;E±2分别为1层与2层能量的导带.AA堆叠3层扶手型石墨烯纳米带的本征能量为
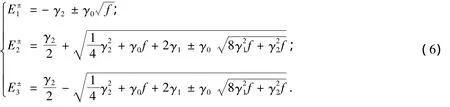
式(6)中:E-1,E±3为能量的价带;E+1,E±2为其导带.AA堆叠4层扶手型石墨烯纳米带的本征能量为
式(7)中:E1±为能量的价带;E2±为能量的导带;γ1为具有相同坐标(x,y)两A原子之间的跳跃能积分;γ1'为最近邻层中A和B原子之间的跳跃能积分;γ2为次近邻层中两A原子之间的跳跃能积分;γ2'为次近邻层A和B原子的跳跃能积分;γ3为三近邻层两A原子之间的跳跃能积分;γ3'为三近邻层A和B原子的跳跃能积分.
1.2.2 AB 堆叠法
当双层AGNRs在x方向上相差a(碳与碳原子之间的距离)相位时,如图2所示,AB堆叠双层AGNRs,半数碳原子直接对应到相邻层的碳原子(标记为B与A'重叠这一类型的原子),另一半碳原子则直接对应到相邻层碳原子环的中心(标记为B'这一类型的原子).因此,AB堆叠与 AA堆叠双层AGNRs在几何结构上有显著的不同,进而导致了物理性质上的变化.为了解出能量,由薛定谔方程得到哈密顿矩阵仍是一个4×4矩阵:
其中:H11,H12,H21,H22均为2 ×2 的方阵.最后解得本征能量为

式(8)中:β0为同层最近邻跳跃能积分;β1为相邻两层具有相同坐标的B原子与最近邻A'原子的跳跃能积分;β2为相邻两层具有不同坐标的A原子与最近邻B'原子的跳跃能积分;β3为相邻两层具有不同坐标的A(B)原子与最近邻A'(B')原子的跳跃能积分;E±1为双层能量的导带;E±2为双层能量的价带.
2 讨论与分析
2.1 AA堆叠双层AGNRs与AB堆叠双层AGNRs的能带与能隙
2.1.1 能带结构的变化
前面已经给出双层扶手型石墨烯纳米带不同拓扑结构的能量解析式,经过计算可以得到双层的能带条数已变为4条,比单层的能带条数多出2条,如图3~图5所示.当n=3q+1时,在AA堆叠双层AGNRs结构中存在着2条水平的导带和价带,其能带标记为p=(n+1)/2,如图4(a)中水平能带为n=7,p=4时的取值;但AB堆叠双层AGNRs的2条水平导带与价带却发生了弯曲的现象,即随着kx的变化而变化,如图4(b)所示.当n=3q+2时,AA堆叠双层AGNRs结构中2条导带与价带分别交于2点,在相交处也有部分区域重叠到了一起,即出现了导带与价带区域交叠现象;而AB堆叠双层AGNRs则不然,导带和价带相交于一点,并没有出现能带交叠现象,如图5所示.

图3 当n=6时,AGNRs的能带图

图4 当n=7时,AGNRs的能带图

图5 当n=8时,AGNRs的能带图
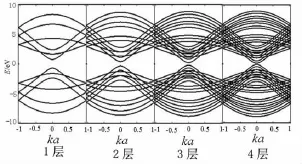
图6 当n=6时,AGRNs的能谱图
2.1.2 能隙的变化
当n=6时,AA堆叠与AB堆叠双层AGNRs的能隙分别为Δd=0.747 1 eV,Δa=1.250 1 eV;当n=7时,能隙分别为 Δ'd=0.987 2 eV,Δ'a=0.673 7 eV.由上述计算结果可知:当 n=3q,n=3q+1 时,AGRNs有着2种不同的能隙结构;当n一定时,AA堆叠双层AGNRs的能隙值小于AB堆叠双层AGNRs的能隙值,即双层AGNRs由于堆叠方法的不同使带隙也相应地发生变化.
2.2 堆叠层数对能带与能隙的影响
2.2.1 能带结构的变化
1)计算发现,随着层数的增加,能带的数量也在相应地增长,其规律是h=2ni,h表示能带条数,n表示纳米带的宽度,i=1,2,3,…,m表示层数,如图6所示.
2)当n=3q+1时,不论层数的多少均存在着一条水平的导带和价带,其能带标记为p=(n+1)/2,如图7中水平能带为n=7,p=4时的取值.这2条水平导带和价带不随着kx和n而变化,但随着层数的增加,这2条水平带也在相应地增加,并具有一定的规律性.1层时,水平导带和价带均分布在E=±3 eV处;但到2层时,2条水平导带和价带在以E=±3 eV为对称轴上均匀地上下分开;3层时,3条水平导带和价带以其中一条为对称轴均匀地上下分开;4层时,4条水平导带和价带同双层有相似结构.这说明当i为奇数层时,水平的导带和价带会以其中一条为对称轴上下均匀地分开,并且各个条带之间成等间距分布;当i为偶数层时,各个条带仍为等间距分布.
3)当n=3q+2时,随着层数的增加AGNRs仍为金属性,导带和价带交在一点上.但不同的是,由于层数的增加,导带和价带的交点也随之增加,同时层与层之间的导带与价带都交叠在一起,并且交叠的区域也随之增大,如图8所示.

图7 当n=7时,AGRNs的能谱图

图8 当n=8时,AGRNs的能谱图

图9 层数对能隙的影响
2.2.2 能隙的变化
当n=6时,各层的能隙分别为Δ1=1.467 1 eV,Δ2=0.747 1 eV,Δ3=0.448 2 eV,Δ4=0.235 0 eV(其中能隙 Δ的下脚标代表着扶手型纳米带层数);n=7时,各层的能隙分别为Δ'1=1.393 7 eV,Δ'2=0.673 7 eV,Δ'3=0.374 9 eV,Δ'4=0.161 6 eV.计算结果显示,当 n=3q,n=3q+1 时,少层的AGRNs仍有着2种不同能隙结构.在这2种不同的情况下,当层数增加时,能隙随之变化如图9所示.
当n值给定时,由于层数的增加,AGRNs的能隙在不断地减小.随着导带与价带的带隙不断减小,电子的跃迁能量就会随之减小.当纳米带层数增加到一定数量时,能隙将会减小到零,即为金属性.这时多层的2维AGRNs便可看成3维石墨,并具有良好的导电性能.另外,当n值增加时,AGRNs的能隙也在不断地变化[11].这样便可以通过改变AGRNs宽度与厚度(即n的大小与层数的多少)来调节能隙的大小.
3 结论
考虑层与层之间的相互作用时,笔者利用紧束缚模型分别计算了双层不同堆叠方法的AGNRs以及少层AGNRs的能量本征值的解析式,并讨论了AA堆叠与AB堆叠双层AGNRs与少层AGNRs的能带结构与能隙变化.在n=3q,n=3q+1,n=3q+2这3种情况下,对各个层AGRNs的能带结构与能隙大小进行对比并发现:改变双层AGRNs的空间几何结构,可以使得能带结构与能隙大小相应地改变;随着层数的增加,能带的数量也在相应地呈规律性增长,能隙的大小在不断地减小;当n=3q+2时,水平的导带和价带随着层数的增加出现规律性的分布;当n=3q+2时,导带与价带之间出现了区域交叠的现象,并随着层数的增加,交叠区域越来越大.
[1]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306:666-668.
[2]Michaël B,Vasilopoulos P,Peeters F M,et al.Bilayer graphene with single and multiple electrostatic barriers:band structure and transmission[J].Phys Rev B,2009,79(15):155402.
[3]Rahul N,Leonid L.Quantum anomalous hall state in bilayer graphene[J].Phys Rev B,2010,82(11):115124.
[4]Sadowski M L,Martinez G,Potemski M.Landau level spectroscopy of ultrathin graphite layers[J].Phys Rev Lett,2006,97(26):266450.
[5]Ferrari A C,Meyer J C,Scardaci V,et al.Raman spectrum of graphene and graphene layers[J].Phys Rev Lett,2006,97(18):187401.
[6]Novoselov K S,Geim A K,Morozov S V,et al.Two-dimensional gas of massless Dirac fermions in graphene[J].Nature,2005,438:197-200.
[7]金子飞,童国平,蒋永进.非近邻跳跃对扶手椅型石墨烯纳米带电子结构的影响[J].物理学报,2009,58(12):8537-8543.
[8]Reich S,Maultzsch J,Thomsen C.Tight-binding description of graphene[J].Phys Rev B,2002,66(3):035412.
[9]Zheng H X,Wang Z F,Luo T,et al.Analytical study of electronic structure in armchair graphene nanoribbons[J].Phys Rev B,2007,75(16):165414.
[10]Edward M C,Vladimir I F.Landau-level degeneracy and quantum hall effect in a graphite bilayer[J].Phys Rev Lett,2006,96(8):086805.
[11]Wallace P R.The band theory of graphite[J].Phys Rev,1947,71(9):622-634.

