一般矩阵特征值的相对扰动上界

孔祥强

（菏泽学院 数学系，山东 菏泽 274015）

一般矩阵特征值的相对扰动上界

孔祥强

（菏泽学院 数学系，山东 菏泽 274015）

利用矩阵的约当分解、Schur三角分解以及计算技巧，深入探讨了任意矩阵特征值的相对扰动问题.在矩阵特征值绝对扰动的基础上，得到了全新的任意矩阵特征值的相对扰动上界，所得结果推广了原有的结论.

矩阵特征值；相对扰动上界；绝对扰动上界

对矩阵特征值扰动理论的研究，已取得了丰富的成果.文献[1]和[2]重点研究了矩阵的乘法扰动，文献[3]研究了奇异的可对角化矩阵的加法扰动，得到了绝对扰动意义下的扰动上界.但对于相对扰动意义下的特征值，得到的成果不多，尤其是在一般性矩阵的研究方面，成果更是有限.本文利用矩阵的Schur三角分解等，得到了适用于任意矩阵的相对扰动上界.

1　几个定义和引理

定义1[4]（正规矩阵）若矩阵A∈Cn×n，满足AHA=AAH，则A为正规矩阵；若满足AH=A-1，则A为酉阵.

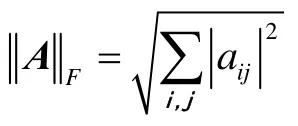
引理1[7]设A为正规矩阵，B=A+E，则存在1,2,…,n的某个排列π，使得

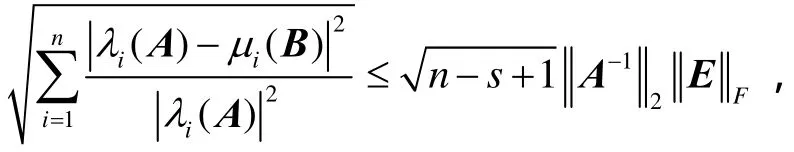
其中，UHBU=Λ+diag(Δ,Δ,…,Δ)，U为酉阵，Λ是由B的特征值构成且与Δ的阶数相对应的对角阵，1≤s≤n，Δi(i=1,2,…,s)为严格上三角阵.

引理2[8]设A和B为任意的n×n矩阵，则存在1,2,…,n的某个排列π，使得

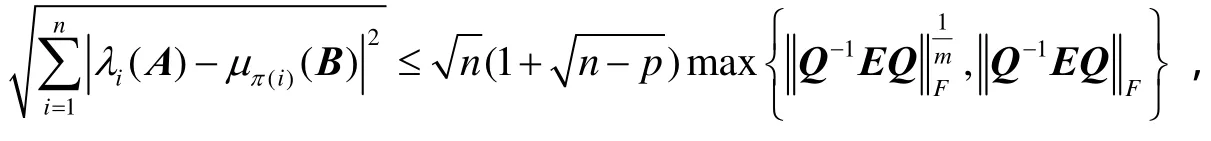
其中，Q-1AQ=diag(J1,J2,…,Jp)为A的约当分解，m为最大约当块的阶数.

2　主要结果

在引理2特征值绝对扰动上界的基础上，我们得到了下面的相对扰动上界定理.

定理 设A,B∈Cn×n，且A为非奇异矩阵，则存在1,2,…,n的某个排列π，使得

证明 对A进行约当分解，即Q-1AQ=diag(J1,J2,…,Jp)，约当块的形式为

设T=diag(T1,…,Tp)，则T可逆，从而

又Σ为正规阵且可逆；T-1Q-1BQT与B有相同的特征值，且有与B的Schur三角分解式相一致的分块.由引理1知，存在1,2,…,n的某个排列π，使得

证毕.

注 1）从证明的过程中不难发现下面的结果成立：

该结果比定理中的上界还要小.

此即为引理1的结果，因此式（3）的结果是文献[7]中定理的进一步推广.

［1］ LI Rencang.Relative perturbation theory I： Eigenvalue and singular value variations ［J］.SIAM Journal on Matrix Analysis and Applications,1998,19（4）： 956-982.

［2］ LI Rencang.Relative perturbation theory III： More bounds on eigenvalue variation ［J］.Linear Algebra and Its Application,1997,266（15）： 337-345.

［3］ EISENSTAT S C.A perturbation bound for the eigenvalues of a singular matrix ［J］.Linear Algebra and Its Application,2006,416（2-3）： 742-744.

［4］ 蒋正新，施国梁.矩阵理论及其应用［M］.北京：北京航空学院出版社，1988： 95-99.

［5］ 熊洪允，曾绍标，毛云英，等.应用数学基础［M］.天津：天津大学出版社，1994： 72-74.

［6］ 孙继广.矩阵扰动分析［M］.北京：科学出版社，2001： 10-226.

［7］ 莫荣华，黎稳.Hermite矩阵特征值的新扰动界［J］.应用数学学报，2006,29（6）： 1033-1038.

［8］ GOLUB G H,VAN LOAN C F.矩阵计算［M］.袁亚湘，译.北京：科学出版社，2002： 19-351.

[责任编辑：熊玉涛]

Upper Bounds of Relative Perturbation for Eigenvalues of Arbitrary Matrices

KONG Xiang-qiang
(Department of Mathematics,Heze University,Heze 274015,China)

The relative perturbation problem of eigenvalues of arbitrary matrices is investigated using the Jordan decomposition of matrixes,the Schur triangular decomposition and the calculating techniques for matrixes.The new upper bounds of relative perturbation of arbitrary matrices are obtained on the basis of the absolute perturbation of matrices and the results generalize the original conclusions.

matrix eigenvalue; upper bounds of the relative perturbation; upper bounds of the absolute perturbation

O241.6

A

1006-7302（2016）01-0012-03

2015-07-14

2013年菏泽学院重点课题组项目（201311）

孔祥强（1983—），男，山东菏泽人，讲师，硕士，研究方向为计算数学.