基本粒子的结构分析

冯彪

（湛江技师学院 职业教育研究所，广东 湛江 524037）

基本粒子的结构分析

冯彪

（湛江技师学院 职业教育研究所，广东 湛江 524037）

根据宇宙球面空间时空四维流形的变模效应，对基本粒子的结构特征进行分析，在变模角的基础上计算粒子的质量、寿命并对粒子的电荷、自旋和衰变方式进行解释.

基本粒子；球面空间；时空流形；变模效应

人类所处宇宙空间是时空四维球面空间，由于光速极限和红移效应，宇宙空间平分为可测和不可测两部分.由拓扑学可知n维欧氏空间En与去掉一点｛D｝的n维球面空间Sn是同胚的，人类认识宇宙空间是基于观测者对所处观测系作为球面空间的特殊点｛D｝（如宇宙中心），从而使宇宙空间各点具有差异性并成为可测性的逻辑起点.各种物理量的量度是对时空流形不同特征的量度，各物理量值之间的关系其实质是时空流形的几何关系［1］.

1　几何空间与物理空间

几何空间是人类思维主观抽象的数学空间（例如：欧几里得空间，简称欧氏空间），而物理空间是物质空间；人类所处的宇宙空间是包含物质及其运动的物理空间.物质结构就是时空流形的拓扑结构，基本粒子的结构分析也就是基本流形的时空分析.人类以欧氏空间为参照基准去认识、表达、测度物理（质）空间.由于宇宙空间作为物理空间是时空复空间，即Ω⊥Τ，用四维坐标可表示为：三维空间Ω=Ω（x,y,z），一维时间T=ict.宇宙圆周如图1所示（其中R是宇宙圆周的半径，δ为变模交角）.宇宙空间中事物的质通过量来描述并由量所构成，而量由可测性来确定，可测性的量度则由测模决定.质量和能量等物理量则通过运动效应（变模效应）来表现.四维球面空间（等价于欧氏五维空间）的投影是欧氏空间的四维球，五维降为四维产生变模效应，可类比常模空间中的投影积聚性或投影变形系数来理解宇宙空间，变模交角可理解为投影角.

图1　四维宇宙球面空间和欧氏空间坐标系示意图

2　时空流形与基本粒子

宇宙空间的四维时空流形经变模后既可表现为光波，也可积聚为粒子；为便于理解球面时空流形与光子、光波的关系，可通过如下各种形式表达：

1）四维球面时空流形在欧氏空间中的投影是四维球，具有超对称性，可用四维正多胞体表达.

2）质量、电量、能量均是人类所处三维空间中的标量，可将三维空间合并理解成一维，R（x,y,z）=R，则四维球面成为二维圆周（宇宙圆周）.

3）球面流形的投影是简谐振动形成光波，一个光波长对应2π周角，由于一半可测另一半不可测，因此，整个球面流形对应周角为4π，一个光波长对应半个球面流形.

4）球面时空流形表现为粒子或波，取决于曲率（或半径）和投影（变模）方式；介于粒子和波之间临界状态的流形作为测量基准，称为基准流形（光基量子），其曲率和半径分别记为：ρ0和R0.

2.1时空流形的连续性与量子化

由图1的宇宙圆周可知，球面空间（时空流形）具有连续性（投影表现为波动性），光子（波）的可测性是时空流形具有可测性的充要条件.由于人类观测手段的极限性（测不准，分辨率/精度局限）导致“可测性”存在极限，因而有最小量子，由此对连续的时空流形产生不连续的观测结果而得到粒子性（即量子化）.粒子虽然是量子化（不连续）的，但其所在球面空间却是连续的，任一粒子的时空流形在宇宙球面空间中都是连通的，这种连通性是量子纠缠现象的根本原因.

2.2时空流形的势与投影（变模）积聚性

由于球面空间无中心（也可说处处是中心），无特殊点、无差异性，所以是全对称性的.在相同维度下，球面空间对称度最大，超对称（四维或以上）欧氏空间的对称度又大于常对称（三维或以下）欧氏空间的对称度，球面时空流形在投影（变模）过程中，因空间维数减少导致“对称性破缺”（对称度降低）而产生投影积聚性形成物理量.全对称的四维球面投影到四维欧氏空间的投影积聚性——投影量P等于四维欧氏空间中的体积V（E4）与四维球面空间（等价于五维欧氏空间）中的体积V（S4）之比，即投影量（物理量）

式中Kp是投影比例（物理量量纲）系数（常数），令KP=Km（常数）为质量m的量纲系数，则质量

由于人类观测者将所处位置作为测量基准点（宇宙中心），从而使球面空间产生“人为”的差异性（可测性），空间各处时空流形具有不同的势（简称形势）.形势的测量可用流形惯性的改变量来量度，惯性（势差为0）的改变量等于势差.时空流形的惯性有两种等价的基本形式：

1）静止——由于静止是相对的，因此静止态是计算时空流形时假想的参照态，时空流形惯性的改变就是“化曲为直”——弯曲空间投影到平直的欧氏空间，质量可按式（2）来表达.

2）匀速直线运动——速度不变.惯性的改变量可用速度的变化率（加速度）来量度，速度的改变可以是大小不变而方向变化.在图1所示宇宙圆周中，可理解为时空流形作匀速圆周运动，其加速度是，令Ke为能量E的量纲系数（常数），则物理量（能量）

同理令ΔE·Δt=Δmc2·Δt=Δmc· cΔ t=Δp·Δx，得

式（4）、（5）就是海森伯（W.Heisenberg）测不准原理的表达式.可见时空差异性形成基本粒子的形势，流形的势反映了变模效应，是宇宙空间产生质量、能量等物理量的起源，也是宇宙万物运动、变化发展及其相互作用力的根本原因.量纲是测量参数的转换，光基量子（基本流形）是测量的基元，测不准原理则显示测量精度.以测不准式中的临界状态（式中取等号“=”的状态）为基准，波长小于（频率大于）临界态表现为粒子性，反之为波动性.

3　基本粒子的结构参数

基本粒子的质量m、电荷q、自旋J、寿命τ等物理量均取决于其时空流形的结构参数，是变模角δ的函数.确定了基本粒子的变模角就能计算粒子的物理量值，分析其结构关系和衰变方式.

3.1基本粒子的变模角与质量

由图1中的宇宙圆周可见，球面时空流形变模效应的大小取决于其测模值和变模角.以光基量子为计算基准时，可将测模值变换成同一基准的变模角来比较，基本粒子的变模角可分为两部分：

1）形状变模角δR——反映时空流形（测模值）的大小，按弧度制定义，δR与R成反比.

2）方位变模角δW——反映基本粒子的时空流形在四维正十六胞体结构中的方位.

设图1所示宇宙圆周的坐标系逆时针方向为正向（正粒子），则反向为反粒子.以第0层的基准流形为计算基准，各层结构中基本粒子的变模角如下：

第0层——正单形的光基量子1个，其形状变模角为0，位置变模角为.

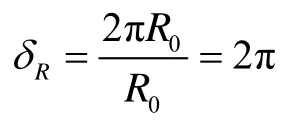
由此可知，基本粒子的种类共有（1+ 8+64+512）×2=1 170个，式中乘以2表示任一基本粒子均有反粒子（因为任一流形均有正反两向），括号内4个加数项依次为第0层、第1、2、3层粒子种类的数量.为此，基本粒子的符号分别用B（n1）、B（n1,n2）、B（n1,n2,n3）表示，粒子的质量（本文所述质量均为静质量）取决于其质量变模角，粒子的质量变模角δm等于形状变模角δR与位置变模角δW相加，即δm=δR+δW.由于表达时空流形物理量的质量、能量两种形式等价，因此其变模角也有两种等价形式：1）以能量的形式度量——变模角是测模与时间虚轴T（ict）的夹角iδ；2）以质量的形式度量——变模角是测模与空间实轴R（x,y,z）的夹角δ.又由于质量、能量具有互相转化的质能关系式，因此时空复空间中是复数与时间T（ict）的夹角（负号表示顺时针方向）.

质量

3.2基本粒子的电荷与自旋

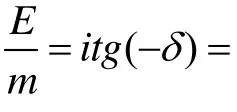
3.3时空流形的作用力与对称性

时空流形的投影（变模）变换，又称为（形/影变换、S/ P变换），S/ P变换具有乘积运算.时空流形间的作用力大小正比于流形势差的数量积，由于数量积满足乘法交换律，因此，物质间的相互作用力服从牛顿第三定律——作用力与反作用力相等.

球面空间的时空流形在欧氏空间中的投影（变模效应）有两种基本形式：

1）在空间轴（实轴）R（x， y,z）上的投影表现为质量（静止的、“实”的能量），流形间的相互作用力表现为万有引力和强相互作用力（见图2中R（x， y,z）轴所示）；

2）在时间轴（虚轴）T（ict）上的投影表现为能量（运动的、“虚”的质量），流形间的相互作用力表现为弱相互作用力（见图2中T（ict）轴所示）；又由于正物质世界R（x， y,z）＞0，故万有引力和强相互作用力只有单一方向的“吸引”作用；

而时间轴T（ict）有正负两个方向，因此弱相互作用力的表现形式既有“吸引”也有“排斥”两种情形.

图2　四种作用力与流形的投影关系示意图

四种基本作用力（不计万有虚力）在时空流形中是统一的（见表1），宏观上由基本粒子组成原子、分子以至宇宙万物均是时空流形的拓扑叠加，其力的作用形式与基本粒子间的作用力是一致的.

表1　四种基本作用力

在图1所示的宇宙圆周上，每一个测模都有正反（逆、顺时针）两个方向的变模角，将变模角代入粒子结构参数公式计算可知，正粒子与反粒子具有相同的质量、自旋量子数和相同的寿命，但带有等量异号电荷或磁矩方向相反，电中性的粒子（如光子）是它们自己的反粒子.正、反粒子（物质）都有相同的正质量但电荷相反，而正、负物质则是质量（能量）分正、负，负质量（能量）是负空间的.另一方面，时空流形的对称性对应守恒量，由于宇宙球面空间中一半可测，一半不可测（时间坐标轴是正负空间的交界）而有可能导致某些物理守恒量发生变化，如图2中所示时间轴上有弱相互作用力的两流形存在负空间部分而导致对称性破缺使宇称不再守恒.

4　基本粒子的寿命与衰变规律

粒子的寿命就是这个粒子产生以后到衰变前存在的时间，当粒子作高速运动时，由于相对论效应，观测到粒子的寿命比它静止时要长，反映粒子不稳定性的物理量是粒子静止时的寿命，本文以基本粒子的时空流形相邻两态持续的时间定义粒子的寿命，并以光基量子的红移效应进行计算.基本粒子的平均寿命τ是其时空流形发生红移效应（变模角由δ1红移到δ2）的持续时间：τ=，而V=csinδ，得，

式中δ1、δ2分别是粒子衰变前、衰变到最近粒子（直接产物）的变模角，sinδ是相对论效应值.物质结构是光子（波）的时空流形结构，基本粒子的衰变就是其流形结构的改变，而光的运动是走短程线的，因此基本粒子的衰变过程是以光子（波）走短程线的形式进行，是光子（波）红移的过程.

5　基本粒子参数的计算

表2　部分基本粒子参数表

6　结论

由基本粒子的变模角及其结构参数公式可计算出全部1170种基本粒子的结构参数，据此分析其几何（结构）关系，确定其物理性质.由于基本粒子在四维正十六胞体结构中的分布具有周期性，因此按参数排列可得类似于化学元素周期表的“基本粒子排列表”.基本粒子的衰变过程是时空流形结构变化的过程，由基本粒子组成原子、分子以至宇宙万物均是时空流形的拓扑关系，光速不变性是拓扑不变量，光子（波）走短程线则是时空流形的拓扑路径.宇宙万物的物质结构和变化发展均可通过时空流形的变模变换和拓扑关系运算进行分析，从而掌握事物的普遍联系和变化发展规律.

［1］ 冯彪.宇宙空间的变模分析［J］.五邑大学学报（自然科学版），2012,26（2）： 29-36.

［2］ 冯彪.物质结构的拓扑分析［J］.五邑大学学报（自然科学版），2013,27（1）： 43-44.

［3］ 霍金，彭罗斯.时空本性［M］.杜欣欣，吴忠超泽.长沙：湖南科学技术出版社，1997.

[责任编辑：韦 韬]

A Structure Analysis of the Fundamental Particles

FENG Biao
(Vocational Education Research Institute,Zhanjiang Technician College,Zhanjiang 524037,China)

According to the variable mode effects of the space-time four-dimensional manifold of the universal spherical space,the structure characteristics of the fundamental particles are analyzed,the quality and life of the particles are calculated on the basis of the mode variable angle,and the charge,spinning and the decaying mode of the particles are explained.

fundamental particles; spherical spaces; space-time manifold; the variable mode effects

O411.1

A

1006-7302（2016）01-0015-09

2015-08-08

冯彪（1967—），男，广东湛江人，高级讲师，硕士，研究方向为数学物理.