钢丝绳数学模型及有限元分析

孙土贵，史天录

（五邑大学机 电工程学院，广东 江门 529020）

钢丝绳数学模型及有限元分析

孙土贵，史天录

（五邑大学机 电工程学院，广东 江门 529020）

用UG中的规律曲线建立6×19西鲁钢丝绳、1×6单股钢丝绳三维模型，针对西鲁股第2层和第3层钢丝位置关系进行三次多项式曲线拟合，建立了二者捻角变化的三次曲线关系，保证钢丝绳捻制后同一个旋转周期螺旋捻距的大小相同；同时建立了第3层钢丝螺旋半径与第2层钢丝螺旋半径之比随第2层钢丝捻角变化的三次拟合关系，确保钢丝捻制后两层丝刚好能接触.利用Workbench对1×6单股钢丝绳进行有限元分析，钢丝绳一段固定，对另一端每根丝加载荷.对比了中心丝与侧丝接触应力，理论计算与有限元分析结果误差在3%，验证了模型和网格的有效性.单股有限元最大应力出现在侧丝与侧丝加载变型后相接触点.

钢丝绳；西鲁股；曲线拟合；有限元分析

钢丝绳具有抗拉强度好、柔韧性好、稳定可靠等优点，被广泛用于电缆、重型机械、建筑等建造领域.国内外研究人员对钢丝绳的力学模型和失效机理做了很多工作，如文献［1］的美国学者Costello从几何、力学、微分学等基础理论出发建立钢丝绳的力学模型，预测钢丝绳受载后的响应；文献［2］建立了不旋转钢丝绳三维模型，分析了单股钢丝绳的应力，简化整绳的三维模型并进行有限元分析；文献［3］推导了西鲁钢丝绳的位置关系，分析了捻角对其他参数的影响，对弹性钢丝绳进行了比较全面的分析，提出一些不足之处，如忽略摩擦等，总结了钢丝绳统一方程式.为了更有效地找出钢丝绳的失效点，本文主要针对钢丝绳的结构参数进行拟合和有限元分析，以期为后续钢丝绳建模、二次开发、参数优化等提供理论指导.

1　钢丝绳模型

在钢丝绳中，若干条侧丝围绕中心丝以一定捻角绕制而成股，若干侧股围绕中心股以一定捻角绕制成绳.丝绕成股分为左旋与右旋，股绕成绳也分为左旋和右旋，钢丝绳的旋向取决其最外层侧股绕中心股的旋向.中心股的主要作用是支撑侧股，大多数的钢丝绳由六根侧股围绕中心股组成，但股的侧丝和层数不同.

空间螺旋结构是钢丝绳几何结构的主要特征，西鲁股第2层钢丝与第3层钢丝之间位置关系比较复杂，需要对两者之间的捻角和半径进行定性分析，从而为钢丝绳结构设计与二次开发等提供理论指导.本文建立了西鲁钢丝绳和单股钢丝绳三维模型，利用三次拟合曲线表示钢丝绳参数之间的关系，能更快速推导出钢丝绳的几何参数，减少计算量.为验证钢丝绳理论计算的可行性，采用有限元分析方法对单股钢丝绳受载后的应力应变进行数值分析，从而根据有限元结果最大应力确定钢丝绳最易失效点，并与理论计算值进行比较从而验证钢丝绳模型的可行性.由于西鲁钢丝绳结构较大，网格单元数量多，分析整绳需要的硬件要求高，本文只分析单股有限元.

本文根据微分几何及矩阵相关理论与钢丝的空间螺旋缠绕相结合，从而推导出丝与股的空间三维坐标方程组.根据方程组通过UG软件中的规律曲线功能生成各钢丝的中心线，从而生成钢丝绳的三维实体.推导西鲁股的位置关系方程，把捻角之间的关系，捻角与钢丝半径之间的关系简单利用拟合函数来描述，获得西鲁股第3层钢丝的捻角与半径随第2层捻角的变化规律.

1.1西鲁钢丝绳三维模型

以6×19西鲁钢丝绳为研究对象，设计参数见文献［1］.中心股侧丝、第1层侧股中心丝、外股中心丝都是一次螺旋线；第1层股侧丝、外股侧丝是二次螺旋线.利用UG中的规律曲线建立钢丝的母线，然后对曲线进行扫掠.图1为西鲁钢丝绳的三维实体几何模型与截面示意图.

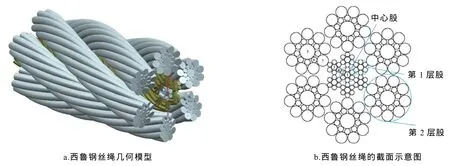
图1　西鲁钢丝绳的三维实体几何模型与截面示意图

1.2西鲁股

西鲁钢丝绳最外层股也称西鲁股，图2为西鲁股内钢丝的几何关系.在西鲁股内，第2层钢丝与第3层钢丝之间是线接触，这样接触应力才能减小从而提高使用寿命.要保证钢丝之间先接触必须满足3个条件：1）两层侧丝的数目相同；2）两层钢丝在一个旋转周期内捻制高度L=2πr tan α相等（r为对应钢丝离中心股中心丝的螺旋半径，α为钢丝捻角）；3）两层钢丝的初相位相差π/m（m为同层侧丝的数目）.文献［3］考虑了每层钢丝间不接触的前提下取Rh/rh=0.99（Rh是绳内股半径或股内丝半径，rh为对应的绳内股螺旋半径或股内丝螺旋半径），限制同层钢丝不接触.为计算两层钢丝捻制高度一样L=2πr tanα，采取三次曲线拟合的方法限定两层钢丝绳间捻角的关系，捻角关系式为

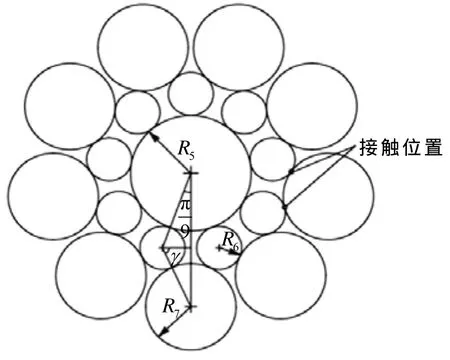
图2　三层钢丝的西鲁股截面示意图

其中，Cα0为三次多项式常数项；Cα1为一次项系数；Cα2为二次项系数；Cα3为三次项系数.

表1列出几种侧丝数m中钢丝7的捻角α7随钢丝6的捻角α6变化的三次多项式常数.

表1　捻角α7与α6之间拟合系数

图3为捻角间关系图，可以看出当每层钢丝数目增加，捻角会增大；随着第2层钢丝捻角不断增大，第3层钢丝的捻角也随之增大，最后都变成90°捻角，说明当第2层捻角接近90°时，钢丝接近直钢丝，第3层变成直线.为了限制第2层钢丝与第3层钢丝之间刚好接触（不镶嵌或不分离），西鲁股中各钢丝半径的位置关系如式（2），为更好计算两层丝之间关系，采用三次曲线拟合的方法表示：

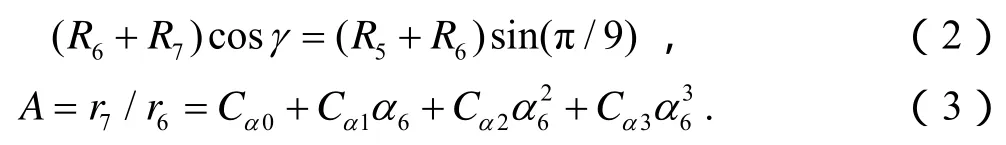
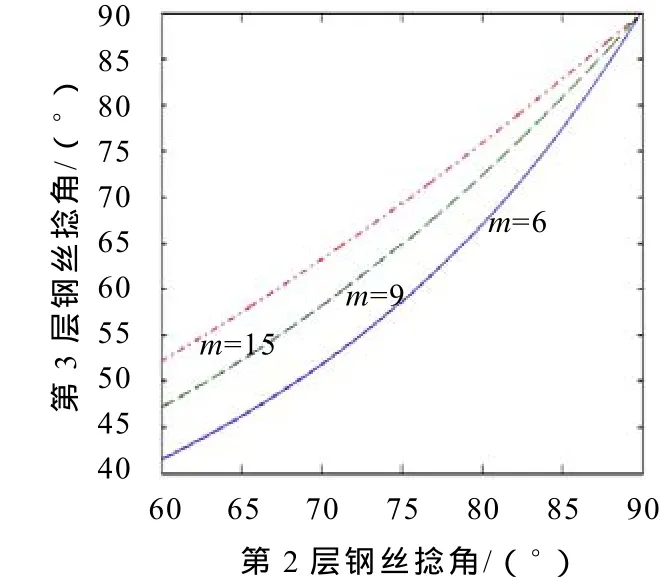
图3　捻角α7随α6的三次拟合曲线

其中，γ为钢丝位置之间的一个夹角；A为第7根钢丝与第6根钢丝螺旋半径之比.表2列出4种不同侧丝数目中A随α6变化的三次多项式常数；图4为这几组数据的三次拟合曲线，从图4可以看出，随着钢丝数目的增加外层钢丝与第2层钢丝半径之比减少；捻角增大，它们之间的比例增大.

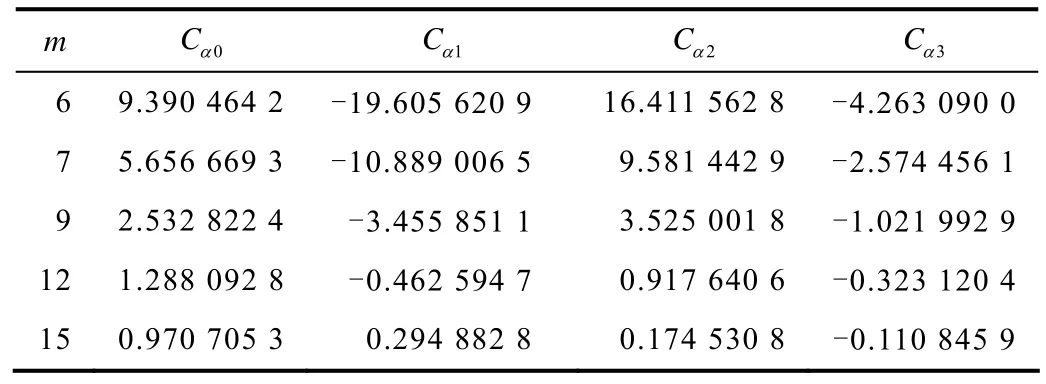
表2　A与α6之间拟合系数

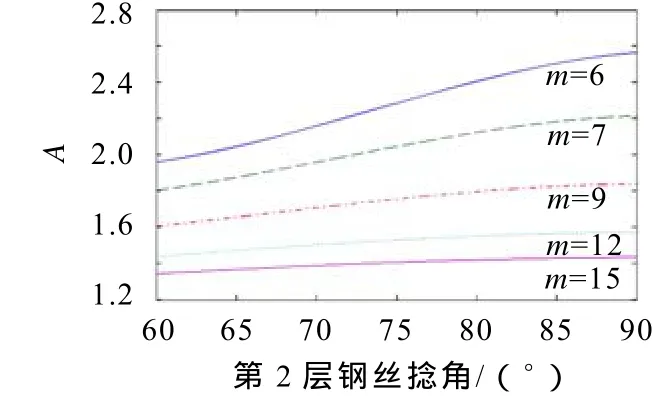
图4　A随α6的三次拟合曲线

2　单股有限元分析

单股钢丝绳是所有钢丝绳的基础结构，对于西鲁钢丝绳结构，其中心股是单股钢丝绳，其第2层股也是由单股结构通过一次空间螺旋缠绕而成.因此，单股钢丝绳的有限元分析是研究西鲁钢丝绳的基础，通过单股分析可以进一步对整绳做有限元分析.而钢丝捻角之间的三次拟合为西鲁钢丝绳的有限元分析、二次开发等减少了计算量.

2.1有限元分析前处理

本次仿真参考文献［1］的单股钢丝绳参数，使用UG建立三维模型，将三维模型导入到Hypermesh中划分网格，利用2D面网格功能中网格划分在每根钢丝端面划分四边形网格，设置划分匹配为圆形端面，然后使用3D功能对实体进行六面体网格划分，网格模型如图5，其中单元数为28 434，节点数为33553.为ANSYS设置单元类型，将penta6单元设置为Solid45并关联到六面体中去.六面体有8个节点，这样的网格能有效地对节点进行约束，且能提高钢丝绳的网格精度.

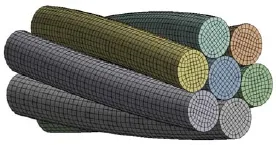
图5　单股钢丝绳的有限元模型

通过ANSYS 中Finite Element Modeler模块导入Hypermesh文件，对钢丝绳一端固定，限制其6个自由度，另一个端面添加拉力.由理论计算各个钢丝的受载比重，中心丝受拉力F1=9 723 N ；侧丝受拉力F2=9 073 N ；丝与丝之间忽略摩擦，因为Costello的模型理论计算中论证了钢丝绳在受载时，摩擦对钢丝绳的影响很小，特别是在小变形情况下.

2.2中心丝与侧丝理论接触应力计算

单股钢丝绳受载后会产生变形，圆截面变成椭圆形.根据Costello的理论计算公式，由钢丝绳钢丝中心线线应力推导出中心丝与侧丝的接触线应力.中心丝与侧丝之间的接触线应力：

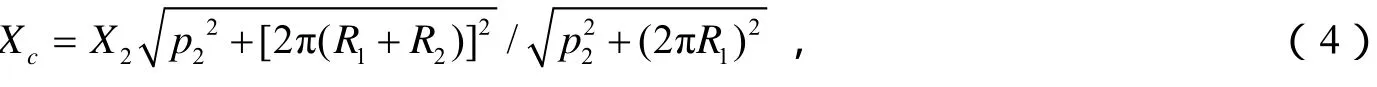
其中，Xc为折合到接触点处单位长度的力；X2为垂直于侧丝母线且通过接触点方向的母线上分力；p2为侧丝的捻距.

钢丝绳中心丝与侧丝的接触应力计算公式：

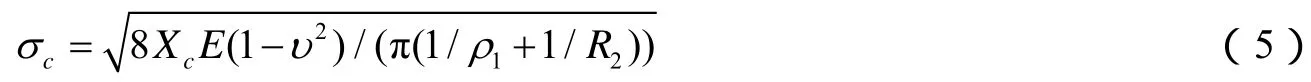
其中ρ1=R1/sin2α2；σc为理论接触点应力；E为弹性模量；v为泊松比；ρ1为变形后中心丝接触点处圆周的曲率半径；α2为侧丝捻角.

把文献［1］的参数代入式（4）和（5），取中心丝受力后应变为0.003，加载条件设钢丝绳自转为0，计算可得钢丝绳的接触应力为1005.9 MPa.

2.3有限元分析结果

经过上述有限元分析，Z轴方向变形云图如图6所示，钢丝绳轴向变形呈层状分布，以钢丝绳中心轴对称分布，说明网格划分均匀及精度能达到计算的要求.钢丝靠近中心股区域变形比远离中心股区域小，符合实际.侧丝比中心丝变形大，但是相差不明显.

图7为单股钢丝绳受载后的应力分布情况.中心丝和侧丝应力相接近，侧丝与侧丝接触处应力比较大，说明应力比较集中，这是由于侧丝受载后，圆形截面变形成椭圆，相邻侧丝相互接触导致应力集中，这和理论数学模型计算结果相符合.侧丝应力比较大，同时反映出为什么钢丝绳绳芯在实际运用中容易松散.

图6　单股钢丝绳变形云图

图7　单股钢丝绳应力云图

文献［2］对仅有3根侧丝的单股钢丝绳的中心丝与侧丝的应力进行了有限元分析，本文利用Workbench中提取实体功能直接对中心丝作分析，应力云图如图8.中心丝与侧丝接触处应力最大，通过式（5）计算可得，单股钢丝绳的理论接触应力计算结果为1005.9 MPa，图8中可以得出钢丝绳有限元仿真计算结果最大接触应力为979.1MPa，两者误差为3%，说明选择的有限元网格类型符合此类钢丝绳模型的分析要求，随着网格再细化，有限元计算结果变动越来越小，网格的精度越来越高.两者之间的误差反映出，参数方程建立起来的三维模型与Costello的力学理论基础能有效的相结合，为钢丝绳整绳有限元分析提供基础.

图8　中心丝应力云图

3　总结与展望

本文利用UG建立了单股钢丝绳和西鲁钢丝绳三维模型，分析了西鲁股内第3层钢丝参数随第2层钢丝绳变化规律，并利用拟合函数表达出来.利用Workbench有限元软件计算了单股钢丝绳受载后的应力响应，将中心丝接触应力的有限元结果与理论计算结果进行了对比，误差在3%，从而验证了三维模型和有限元模型的有效性.

由于钢丝绳受载情况复杂，下一步工作将建立钢丝绳受弯曲后的三维模型，计算钢丝绳接触点的空间坐标与模型做对比，由于西鲁钢丝绳整绳结构庞大，后续可利用工程计算机帮助计算有限元；如单股三层钢丝绳的有限元及理论计算；对西鲁钢丝绳的主要参数进行参数优化；推导西鲁钢丝绳受载后轴向应变与旋转应变之间的关系，分析各个参数对两个变量的影响程度；钢丝绳绕滚轮受载后的力学模型.

［1］ COSTELLO G A.Theory of wire rope ［M］.2nd Edition.New York： Springer,1997.

［2］ 贾尚雨.不旋转钢丝绳的力学特性与失效研究［D］.广州：华南理工大学，2011.

［3］ VELINSKY S A.Design and mechanics of multi-lay wire strands ［J］.Journal of Mechanical Sciences,1988,110（2）： 152-160.

[责任编辑：韦 韬]

Mathematical Model and Finite Element Analysis of Wire Ropes

SUN Tu-gui,SHI Tian-lu
(School of Mechanical and Electrical Engineering,Wuyi University,Jiangmen 529020,China)

A three-dimensional model is established using the curve function of UG for the 6×19 Seale wire rope and the 1×6 single-strand wire rope.Through the curve-fitting of the positional relationship by the third order polynomial between the second and third layers of the Seale wire rope,the third order polynomial relationship between two helix angles is established to ensure that the rope have the same lay length after twisting spiral.At the same time,the third order polynomial relationship of the helix radius ratio between the second and third layers of Seale wire is established to ensure that the two wires can contact with each other.A finite element analysis is made of the 1x6 single-strand wire rope using Workbench.A wire rope is fixed at one end and each strand at the other end is given load.The contact stress on the center wire and the side wire is compared and the theoretical calculation and finite element analysis result error is at 3%.The validity of the model and the gridding is verified.The maximum stress of single strands occurs at the contact point between the side wire and the loaded side wire.

wire rope; seale wire rope; curve-fitting; FEM

TD532

A

1006-7302（2016）01-0064-05

2015-09-16

五邑大学机械制造及其自动化重点学科（2021501）

孙土贵（1989—），男，广东湛江人，在读硕士生，研究方向为钢丝绳仿真、参数优化与数学模型研究；史天录，副教授，博士，硕士生导师，通信作者，研究方向为机电系统可靠性研究等.